Privacy-Preserving Collaborative Filtering Algorithm Based on Local Differential Privacy
Ting Bao,Lei Xu,Liehuang Zhu,Lihong Wang,Ruiguang Li,,Tielei Li
1School of Computer Science and Technology,Beijing Institute of Technology,Beijing 100081,China
2School of Cyberspace Science and Technology,Beijing Institute of Technology,Beijing 100081,China
3National Computer Network Emergency Response Technical Team/Coordination Center of China,Beijing 100029,China
4China International Engineering Consulting Corporation,Beijing 100048,China
Abstract:Mobile edge computing(MEC)is an emerging technolohgy that extends cloud computing to the edge of a network.MEC has been applied to a variety of services.Specially,MEC can help to reduce network delay and improve the service quality of recommendation systems.In a MEC-based recommendation system,users’rating data are collected and analyzed by the edge servers.If the servers behave dishonestly or break down,users’privacy may be disclosed.To solve this issue,we design a recommendation framework that applies local differential privacy(LDP)to collaborative filtering.In the proposed framework,users’rating data are perturbed to satisfy LDP and then released to the edge servers.The edge servers perform partial computing task by using the perturbed data.The cloud computing center computes the similarity between items by using the computing results generated by edge servers.We propose a data perturbation method to protect user’s original rating values,where the Harmony mechanism is modified so as to preserve the accuracy of similarity computation.And to enhance the protection of privacy,we propose two methods to protect both users’rating values and rating behaviors.Experimental results on real-world data demonstrate that the proposed methods perform better than existing differentially private recommendation methods.
Keywords:personalized recommendation;collaborative filtering;data perturbation;privacy protection;local differential privacy
I.INTRODUCTION
Recommendation system has now become a vital and indispensable part of our daily life[1].A recommendation system generally consists of a server and a number of users.Traditionally,the recommendation server is deployed on a cloud platform,and it analyzes data collected from users.Due to the existence of network delay,users may not be able to receive the recommendation results in time.With the development of wireless communication technologies,mobile edge computing(MEC)has become an important computing paradigm.By deploying cloud resources to the edge,MEC can realize swift computing and high storage capacity[2].As shown in figure 1,the aforementioned cloud-based recommendation framework can be recast to a cloud-edge form where the edge servers collect and store users’data so as to perform partial computing task.The cloud computing center collects the computing results from edge servers and computes the recommendation results.By this way,the network delay will not be a major issue that affects user experience.In following descriptions,for simplicity,the edge servers and the cloud computing center are collectively referred to as the recommendation server.
The predominant approach to build recommendation systems is collaborative filtering(CF)[3],where the recommendation server collects ratings from users and predicts the items that users may be interested in.The rating data of users are the fundamental resources of CF-based recommendation,hence the performance of recommendation heavily depends on user participation.However,the rating data released to the server usually contain users’sensitive information,such as health condition,political views or sexual orientation,etc.The privacy issue caused by personalized recommendation has attracted much attention in recent years.
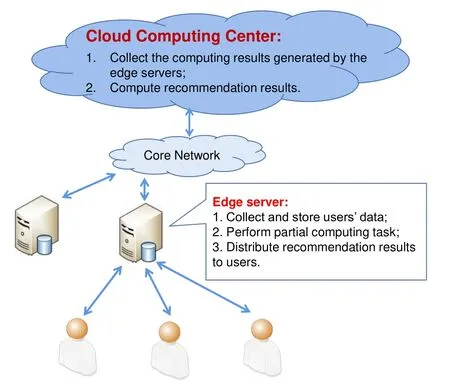
Figure 1.An illustration of the MEC-based recommendation framework.
The privacy policies used in practical recommendation systems are mainly designed to inform the users what kind of information will be collected and why the server collects the information.While from the perspective of users,these privacy policies are not reassuring.To better protect users’privacy,some technological approach is required[4].The privacy protection operations generally cause a decline in data utility which will hurt the recommendation quality.How to balance the degree of privacy protection and recommendation quality is an important question for privacy-preserving recommendation systems[5,6].
To quantify the degree of privacy protection,Dwork et al.[7]introduced the notion of differential privacy(DP).A mechanism that satisfies differential privacy can limit the attackers’ability to infer the absence of any user in a dataset by adding carefully calibrated noise.More importantly,DP can protect users’privacy from attackers with arbitrary background knowledge.Traditionally,the differentially private mechanism is applied to a dataset which consists of the original data records collected from users.The server that collects users’data is assumed to be trusted.However,a trusted server can hardly be found in practice.The server may be vulnerable to security attacks,or the service provider who manages the server may compromise users’privacy on purpose.
Considering the existence of untrusted servers,the user needs to protect his/her privacy on his/her own.Local differential privacy(LDP)[8],as an extension of DP,enables each user to perturb his/her data independently and the server to obtain valuable information by aggregating users’perturbed data.The user does not have to trust the server.LDP provides users with stronger privacy protection than DP but introduces greater noise[9].The recommendation accuracy will inevitably decline after LDP is applied.The technical challenge here is to find a solution that can protect users’privacy while preserving the recommendation accuracy as much as possible.In this paper,we propose an item-based CF recommendation framework which utilizes LDP techniques to protect users’privacy.In this framework,each user’s original rating data are perturbed by the user himself/herself and then released to the server.The server computes the similarities between different items by aggregating users’perturbed data.The results are sent back to each user so that the user can predict the ratings of unrated items.The proposed data perturbation methods not only can provide privacy protection for the original rating values as well as the rating behaviors,but also can reduce the noise generated by perturbation.And we have conducted a series of simulations to demonstrate the performance of the proposed methods.The main contributions of this paper are summarized as follows:
·We design an item-based CF recommendation framework which applies LDP to protect users’privacy.Different from previous studies,the proposed framework requires no trusted server.
·Multiple data perturbation methods are proposed for protecting users’ratings values and/or rating behaviors.Previous studies usually assume that users’rated items and unrated items are equally sensitive,which may cause unnecessary loss of utility.To improve the utility of perturbed data,we propose a method which provides LDP guar-antee only for users’rated items.
·We conduct a series of simulations on real-world data to evaluate the performance of the proposed methods.Simulation results show that the proposed methods can provide strong privacy protection while preserving the quality of recommendation.
The rest of the paper is organized as follows.Section II reviews some studies on privacy-preserving recommendation and local differential privacy.Section III introduces some basics of collaborative filtering and LDP.Section IV describes the proposed recommendation framework.Section V presents in detail how LDP is applied in the proposed framework.Simulation results are presented in Section VI.Finally,conclusions are drawn in Section VII.
II.RELATED WORK
2.1 Privacy-Preserving Recommendation Systems
Early studies[3,10,11]on recommendation systems mainly focus on how to improve the accuracy of recommendations.As people pay more attention to the privacy issue,various privacy-preserving approaches have been proposed for recommendation systems,such as randomization techniques,cryptography techniques,hash techniques and differential privacy techniques.Polat et al.[12]applied randomization techniques to users’original rating data.However,if attackers conduct clustering on perturbed data,user’s rating values can still be inferred with high accuracy[13].Canny et al.[14]introduced cryptographybased approaches to recommender systems to protect users’rating data.Qi et al.[15,16]utilized various hash techniques to provide privacy protection in distributed service recommendation.However,both cryptography-based approaches and hash-based approaches require a trusted service provider and high computation cost.Differential privacy(DP)[7]ensures that an attacker cannot infer an individual’s original data from the output of a randomized algorithm with high accuracy.McSherry et al.[17]applied DP to several leading recommendation systems in the Netflix Prize competition.Jiang et al.[18]proposed a privacy-preserving distributed client-server recommendation framework which relied on a two-stage randomized response algorithm and matrix factorization technique,and their framework was proved to satisfy DP.
2.2 Local Differential Privacy
Traditional DP depends on a trusted service provider,which greatly limits its application[19,20].Local differential privacy(LDP),which requires no trusted service provider,conducts the privatization operation on the user side[21–23].Warner et al.[24]proposed a randomized response(RR)mechanism to perturb private data,which can be used to hide the real answers to sensitive questions.Kairouz et al.[25]proposed the k-RR mechanism which extends the binary alphabet of RR to the k-ary alphabet.To deal with the open alphabet where the set of input symbols is not enumerable,Kairouz et al.[26]proposed the O-RR mechanism which extends k-RR by using hash functions.Erlingsson et al.[27]proposed an algorithm called RAPPOR and implemented it in Google Chrome browser.RAPPOR first encodes the single-valued data into a Bloom filter and then performs RR on each bit of the Bloom filter.The communication cost of RAPPOR is determined by the size of the Bloom filter which is usually high.To solve this issue,Bassily and Smith[28]proposed S-Hist method where each user transforms a string into a randomly select bit,and the single bit is sent to the data collector.However,this method only applies to categorical data.Both the MeanEst method proposed by Duchi et al.[8]and the Harmony method proposed by Nguyeˆn et al.[29]can be applied to the numerical data.
2.3 Recommendation with Local Differential Privacy
Recently LDP have also been introduced to personalized recommendation.Shen and Jin[30]designed an EpicRec framework which applied LDP to protect user’s rating behaviors.In their framework,items are divided into different categories,and EpicRec provides users with category-based privacy control by setting different sensitivity levels for different categories.The shortcoming of this approach is that user’s category preference could be disclosed.Hua et al.[31]applied LDP to matrix factorization(MF)recommendation that can prevent the server from learning users’rating values.However,the user’s rating behaviors could be exposed.In practice,both the rating values and the rating behaviors are sensitive information of users[18].Recently,Shin et al.[32]applied LDP to a MF-based recommendation framework so as to protect users’rating values and rating behaviors simultaneously.In this paper,we apply LDP to a memory-based CF recommendation framework,and propose methods to protect both users’rating values and rating behaviors.
III.PRELIMINARIES
Collaborative filtering(CF)is a prevailing algorithm for building recommendation systems.In this paper,we mainly focus on item-based CF methods and investigate how to protect users’privacy through LDP techniques.To make the paper more self-contained,in this section we briefly introduce some basics of collaborative filtering and local differential privacy.
3.1 Collaborative Filtering Based Recommendation
Consider a set of N users U={u1,u2,...,uN}and a set of M items I={i1,i2,...,iM}.A user expresses his/her opinion about an item by assigning the item a rating value.Let rn,mdenote the rating value that user n assigns on item m.The rating values of all users form a user-item matrix R=[rn,m]N×M(1 ≤n≤N,1≤m≤M).We also introduce a binary matrix Y=[yn,m]N×M(1≤n≤N,1≤m ≤M),where element yn,mindicates whether user n has rated item m.We define yn,m=1 if user n has rated item m and yn,m=0 otherwise.The basic task of a recommendation server is to predict the rating values for items that are not rated by users.
There are several ways to do the prediction.One of the most popular techniques is collaborative filtering.Collaborative filtering can be roughly divided into two categories:model-based algorithm and memory-based algorithm.Model-based algorithm generates recommendation by building a model with users’ratings,such as matrix factorization,clustering,etc.Memorybased algorithm directly utilizes users’ratings to provide recommendation.In this paper,we focus on memory-based CF algorithm.As shown in figure 2,the recommendation server first collects rating values from each user to generate a user-item matrix R.Then,the server computes the similarity of any two users/items and uses the similarity information to find each user’s possible interested items.
The memory-based CF algorithm can be further divided into two types:the user-based algorithm and the item-based algorithm.User-based algorithm employs statistical techniques to find a set of users who have similar interest with the target user n,and these users are called user n’s neighbours.User n’s predicted rating could be computed by his neighbours’rating values and the similarity between user n and his neighbours.Item-based algorithm finds similar items based on users’rating values.Vector cosine similarity is often used to measure the similarity.Denote the set of users who have co-rated item m and z as U′.The cosine similarity between the two items is given by
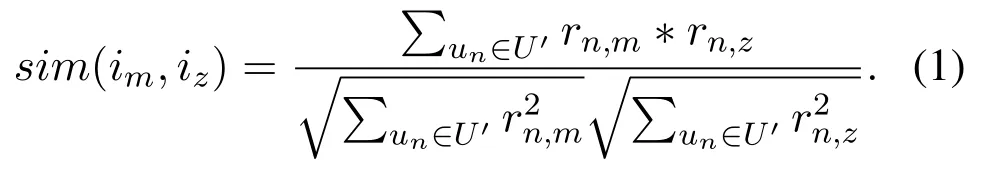
Let Neighbour(im)denote the set of the most similar items to item m.Given Neighbour(im),user n’s predicted rating on item m,denoted as Pn,mis computed by
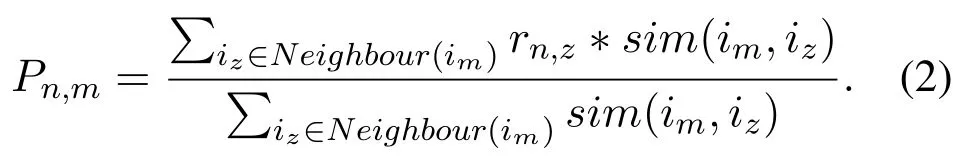
In this paper,we assume that the server is untrusted and users do not want to share their original ratings with the server,hence the prediction is conducted on the client-side rather than the server-side.As mentioned above,the user-based approach needs the neighbours’original rating values to make the prediction.While the item-based approach only involves the target user’s ratings,once the neighbour set is determined.Therefore,we choose item-based CF as the basis of the proposed recommendation framework.
3.2 Local Differential Privacy
Suppose there are N users each of whom owns a private data x defined on an input alphabet X.A basic assumption of differential privacy is that there is a trusted server that holds the private data of all users.Before releasing users’data to others or answering queries of third parties,the trusted server will perturb the data via some randomized algorithm.However,if the server is untrusted, each user should perturb his/her private data before releasing them to the server so that the user’s privacy can be preserved.This is the basic idea of local differential privacy(LDP).A formal definition of LDP[8]is given below
Definition 1.A randomized algorithm Q satisfies ϵlocal differential privacy if and only if for any two input data Xi,Xj∈X and for any possible output x*∈X*of Q,there is
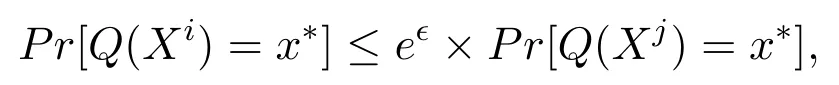
where the probability is over the randomness of Q and the positive parameter ϵ is called privacy budget.
The above definition implies that from the output of algorithm Q,it is impossible to determine what the input data is.When the privacy budget ϵ is quite small,the perturbed data is almost independent of the original data.That is, given the output x*,any data from the alphabet X can be the input.And if the privacy budget ϵ is big enough,it is very likely that the perturbed data x*is identical with the original one.
Sequential composition and parallel composition are two crucial properties of DP[33].As an extension of DP,LDP inherits these properties.A formal description of sequential composition property is given below:
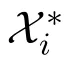
The implementation of ϵ-LDP requires a suitable data perturbation mechanism.Different mechanisms have been proposed to deal with different types of data.The randomized response(RR)mechanism is the most widely used perturbation mechanism for binary alphabet.The k-RR mechanism proposed in[26]can be applied to the case where|X|=k and k>2.However,k-RR is only suitable for categorical data.And when k is big,k-RR will cause a large statistical error.The Harmony mechanism proposed in[29]can be applied to both categorical data and numerical data.Given the original data x,the Harmony mechanism generates the perturbed data x′by sampling from the following distribution
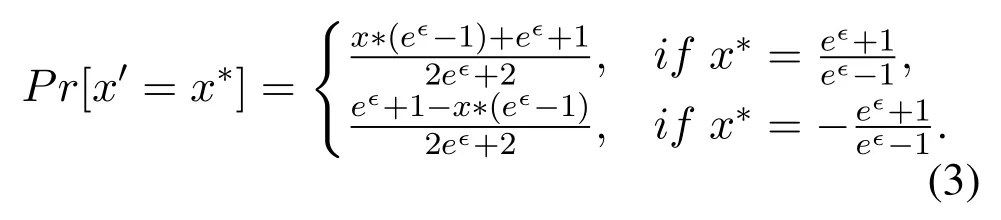
IV.SYSTEM MODEL
To deal with the privacy issue in recommendation systems,in this paper we propose a recommendation framework that incorporates the idea of local differential privacy into item-based collaborative filtering.As depicted in figure 3,in the proposed framework,users do not provide their original ratings to the server.Instead,a user first perturbs his/her ratings in a way that satisfies local differentiall privacy,and then sends the perturbed ratings to the server.The server computes the similarity between items based on the perturbed ratings.The similarity matrix,which consists of similarities of all item pairs,is then sent back to each user.After that,each user makes his/her own predictions according to Eq.(2).In the above procedure,the server cannot access the original ratings of users.Hence users’privacy can be preserved.A formal description of the privacy-preserving recommendation model is given below.
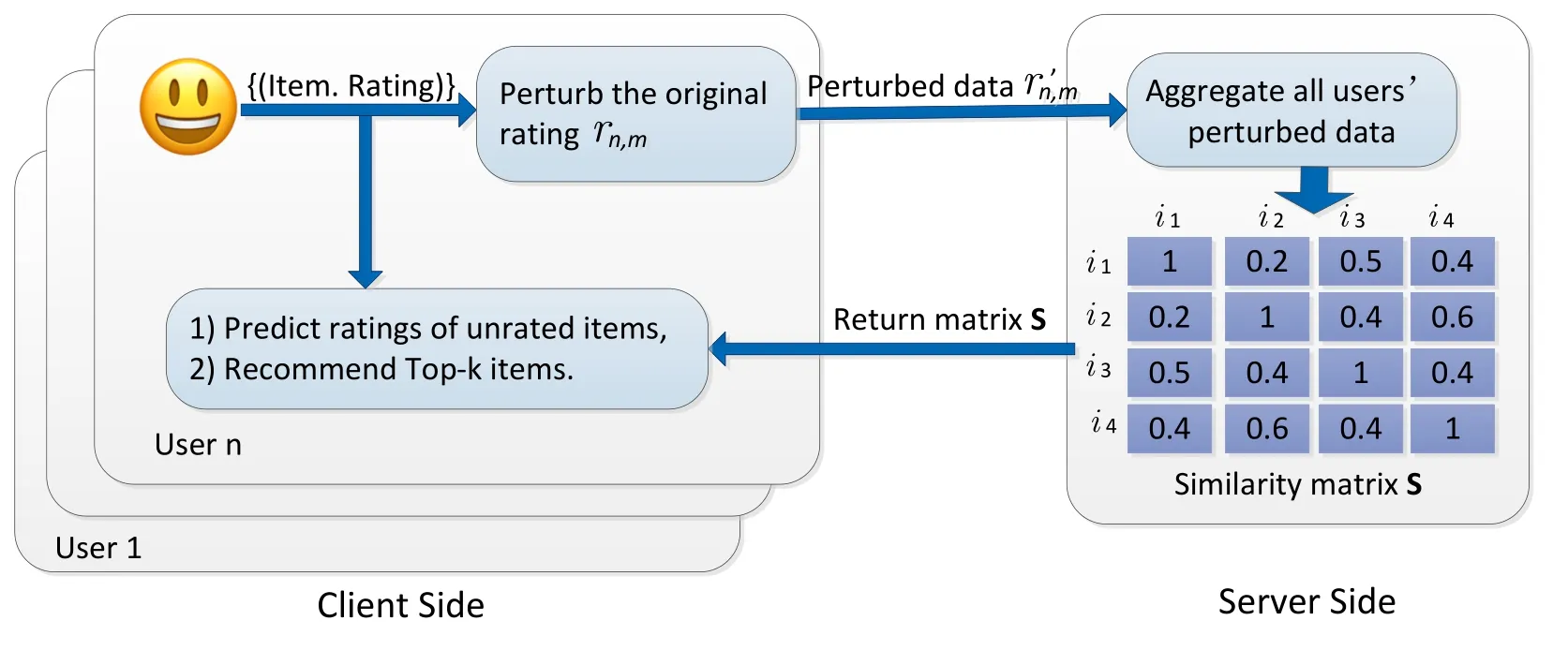
Figure 3.An illustration of the item-based CF recommendation framework with LDP.
where U′represents the set of users who have co-rated item m and z.
The perturbation of rating values will introduce much noise to the computation of similarity.Therefore,the perturbation mechanism should be carefully designed so that the accuracy of similarity computation can be preserved as much as possible.Details of the proposed perturbation method will be presented in Section V.
After computing the similarity between any two items,the server generates an item-item similarity matrix S=[sim(im,iz)]M×M(1≤m ≤M,1≤z≤M).When user n sends a recommendation request to the server,the server returns the matrix S to user n.Then for each unrated item m,the user n can utilize the matrix S to determine the set Neighbour(im)in Eq.(2)and predict the rating Pn,m.After that,user n can get the Top-k recommended items.
V.RECOMMENDATION WITH LDP
In the above section,we have proposed a framework for privacy-preserving recommendation.In this section,we will elaborate how LDP is achieved in the proposed framework.We first design a method to protect users’rating values.Then,we propose a method which also protects users’rating behaviors.To better preserve the accuracy of similarity computation,we modify the proposed method to provide LDP only for users’rated items.A theoretical analysis of the influence of data perturbation on similarity computation is also presented.
5.1 Protecting Rating Values
After collecting each user’s perturbed rating values,the sever computes the similarities between any two items by using Eq.(4).However,the computation results are quite inaccurate.For example,when the server computes the similarity sim(im,iz)between item m and z by using the perturbed ratings,it will get
The denominator in the second line only depends on the cardinality of U′,no matter what the values rn,mand rn,zare.Therefore,it is inappropriate to directly use the perturbed ratings to compute similarities.We propose the following method to preserve the computation accuracy.

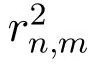
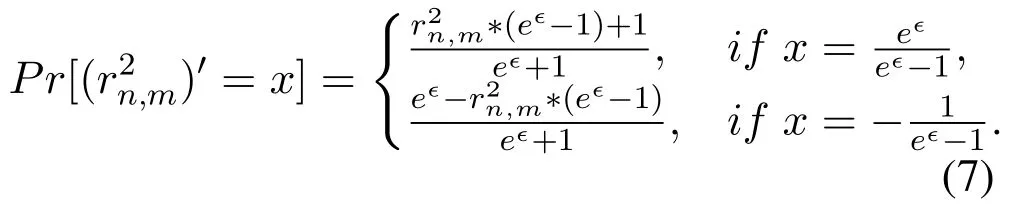
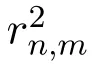
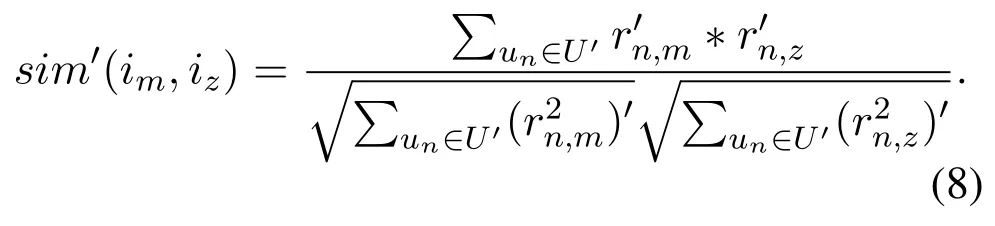
Theorem 1.Algorithm 1 satisfies ϵ-LDP with respect to users’rating values.
Proof of Theorem 1.Given rn,m,let X1,X2be any two values from the domain X=[-1,1].According to Algorithm 1,there is
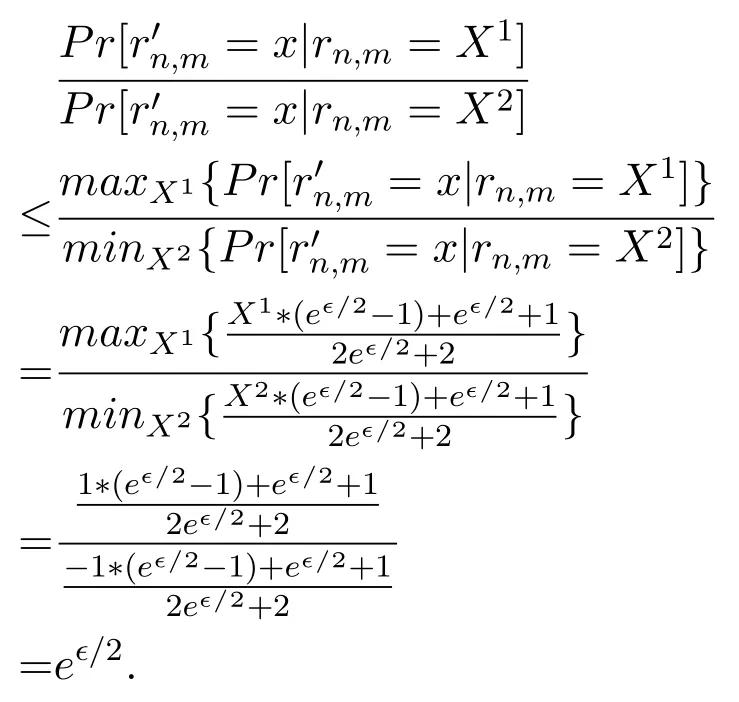
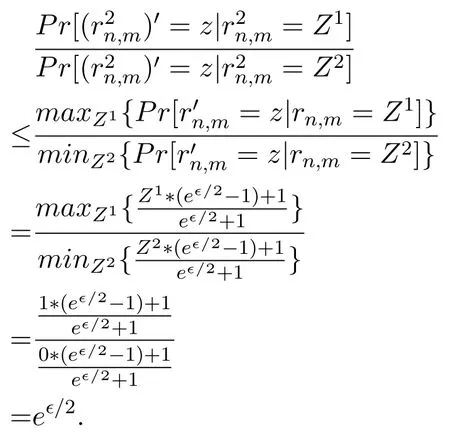
5.2 Protecting Both Rating Values and Rating Behaviors
Other than the rating values,whether a user has rated an item may also disclose the user’s privacy.To enhance the protection of privacy,in this subsection,we propose a method which not only protects user’s rating values but also protects user’s rating behaviors.
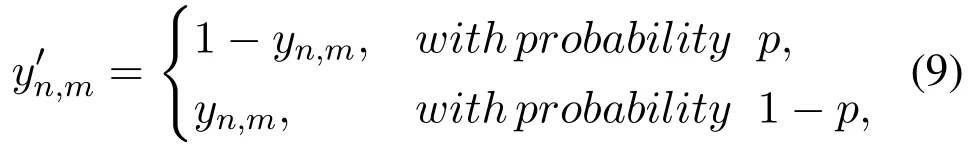
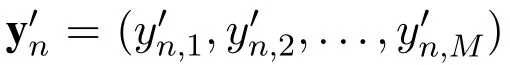
However,the above method has the following issue.

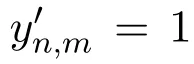
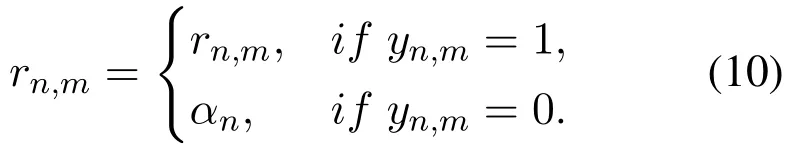
The parameter αnplays an important role in the PVB method.The value of αncan be determined via different ways.We have conducted a series of simulation to evaluate the influence of αnon recommendation accuracy.Details will be presented in Section VI.
Theorem 2.Algorithm 2 provides(ϵ1+ ϵ2)-LDP for both users’rating values and rating behaviors.Proof of Theorem 2.Denote the domain of yn,mas ψ={0,1},and let Y1,Y2be any two values from ψ.According to Algorithm 2,there is
According to Definition 1,we can prove that Algorithm 2 provides ϵ1-LDP for users’rating behaviors.And Algorithm 2 protects users’rating values by using Algorithm 1.Set the privacy parameter of Algorithm 1 as ϵ2,then Algorithm 2 provides ϵ2-LDP for users’rating values.According to the sequential composition property,we can conclude that Algorithm 2 satisfies(ϵ1+ ϵ2)-LDP.
5.3 Enhancing Data Utility
An implicit assumption of the proposed PVB method is that the unrated items are as sensitive as the rated items.However in practice,users only concern the disclosure of their rated items.The PVB method may provide excessive privacy protection and cause unnecessary loss of utility.
·if yn,m=0,
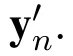

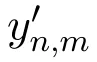
Theorem 3.For users’rated items,Algorithm 3 provides(ϵ1+ ϵ2)-LDP for both rating values and rating behaviors.
Proof of Theorem 3.Given yn,m,let Y1,Y2be any two values from the domain ψ={0,1}.According to Algorithm 3,there is
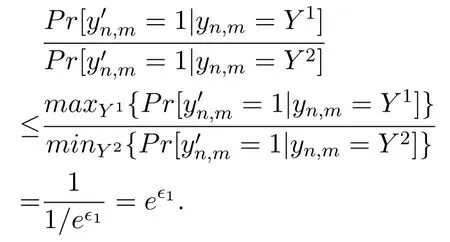
According to Definition 1,we can prove that for users’rated items,Algorithm 3 provides ϵ1-LDP for rating behaviors.And Algorithm 3 protects users’rating values by using Algorithm 1.Set the privacy parameter ϵ to ϵ2,we can get Algorithm 3 provides ϵ2-LDP for users’rating values.According to the sequential composition property,for users’rated items,Algorithm 3 satisfies(ϵ1+ ϵ2)-LDP.
5.4 Utility Analysis
We now theoretically analyze whether the server can obtain accurate similarity between items by using the proposed methods.Since all three methods utilize the same way to perturb users’rating values,here we only analyze the PRV method.
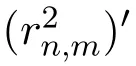
Proof of Theorem 4.By Eq.(7),

Proof of Theorem 5.By Eq.(5),
The following theorem shows that when a sufficiently large number of users participate in the recommendation system,the server can get an accurate estimation of sim(im,iz)by using Eq.(8).
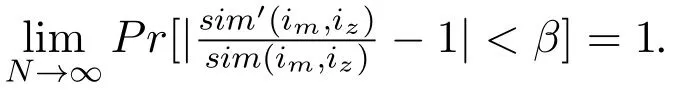
Proof of Theorem 6.See Appendix.
According to Theorem 6,the accuracy of the similarity computation depends on the number of users.In next section,we will conduct simulations to see how the number of users affects the accuracy.
VI.EXPERIMENTAL EVALUATION
In the previous section,we have proposed several algorithms that can realize differentially private recommendation.To verify the feasibility of these proposed algorithms,we have conducted a series of simulations by using real-world data.specifically,we have made a comparison of the proposed algorithms and the matrix factorization-based privacy-preserving recommendation algorithm proposed in[31,32].In this section,we first describe the preparation of datasets and experiment setup,then we present the simulation results under different settings.
6.1 Experiment Settings
6.1.1 Dataset
We conduct simulations on two real-world datasets,namely MovieLens1and Jester2.These data sets are commonly used in the study of personalized recommendation.Given a dataset,we randomly select 70% of the ratings for training,and the rest are used for testing.
The MovieLens data set contains 10 million ratings from 71,567 users on 10,681 movies,and the rating values range from 0.5 to 5.To reduce the negative effect caused by data sparsity,we sample 3,027,450 ratings from 69,832 users on 300 movies.
The Jester data set consists of 181,0455 ratings of 100 jokes submitted by 24,983 users.The rating values range from-10.00 to+10.00(the value “99”indicates “unrated”).To make the simulation results obtained on Jester comparable with those obtained on MovieLens,we adjust the rating values to the range from 0.5 to 5.
6.1.2 Evaluation metric
We evaluate the performance of the proposed methods from the following aspects:
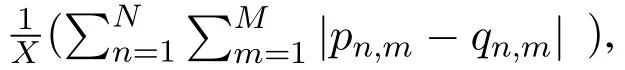
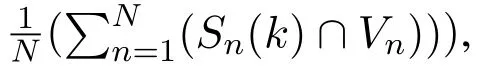
6.1.3 Experiment Setup
The proposed privacy-preserving algorithms are based on item-based CF.To determine the neighbourhood size which has important impact on recommendation quality,we first simulate the basic item-based CF algorithm and test different settings of neighbourhood size.According to the simulation results shown in figure 4,we set the neighbourhood size to 10 in following simulations.Moreover,we have conducted a series of experiments to determine the best way to measure the similarity between items.Five different measurements are tested,including vector cosine,Pearson correlation,adjusted cosine,Euclidean distance and Manhattan distance.Based on the simulation results,vector cosine is chosen for subsequent simulations.
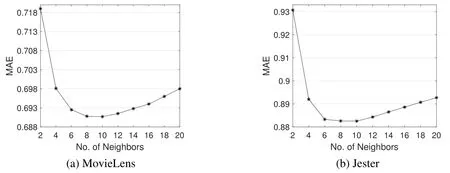
Figure 4.The impact of neighbourhood size on recommendation quality.
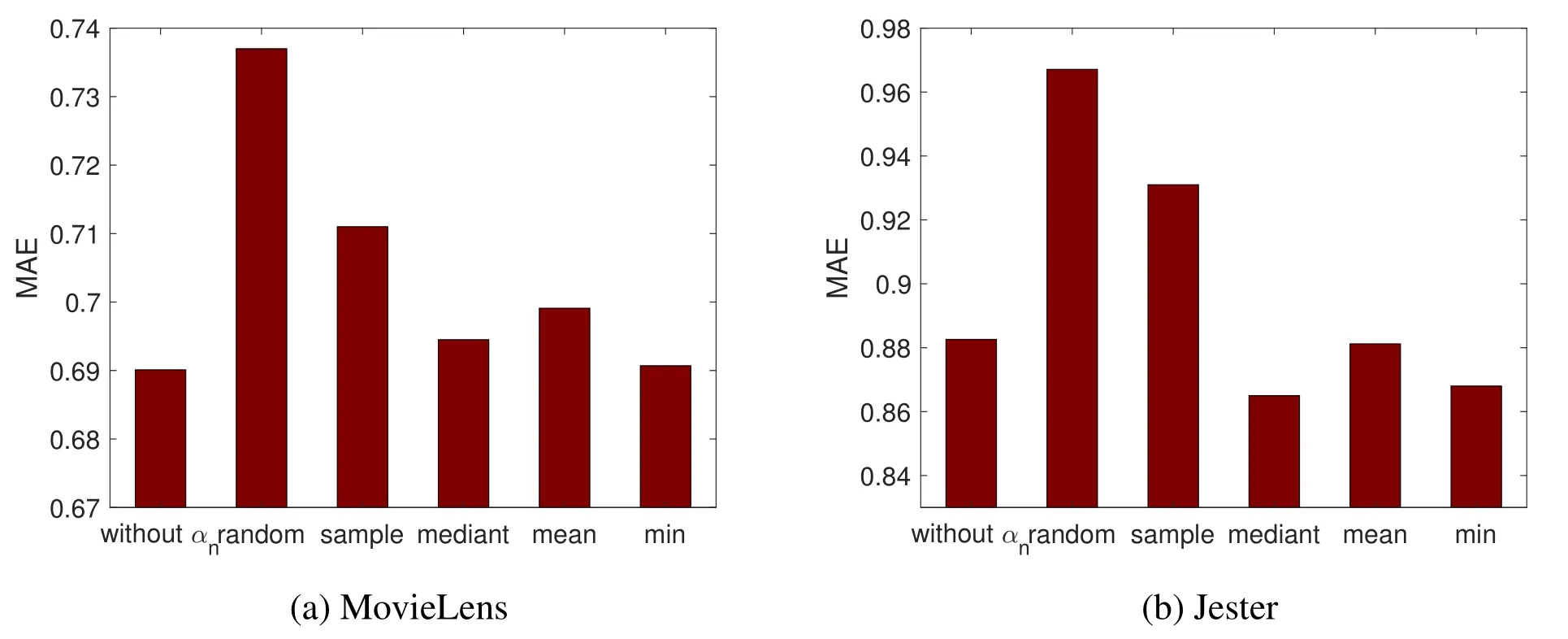
Figure 5.The impact of αnon recommendation quality.
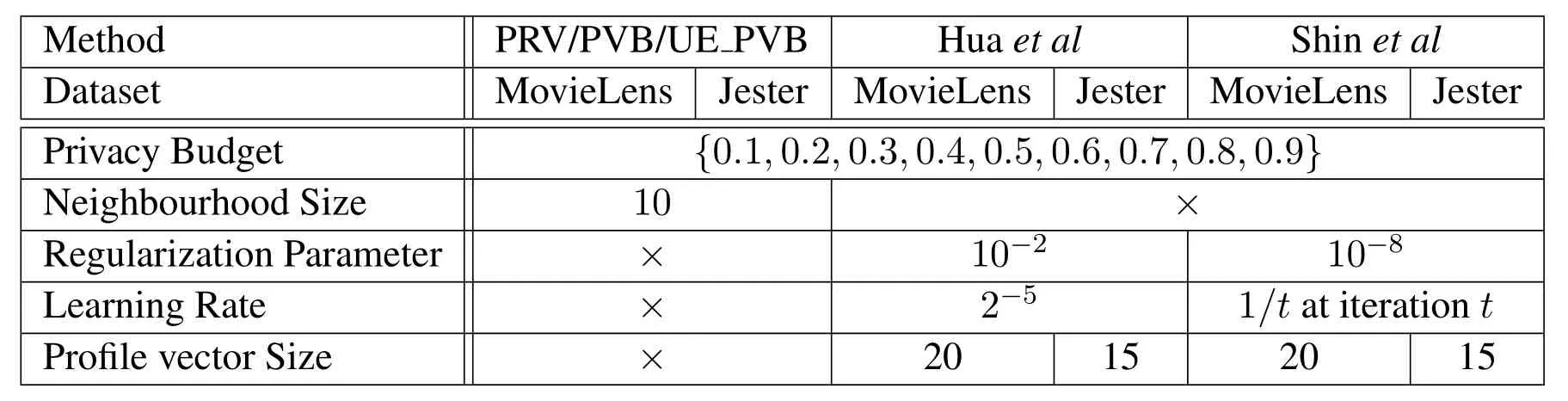
Table 1.Parameter settings for simulations.
6.2 Determine the ‘‘fake” Rating Value
A rating that a user assigns on an item shows whether the user likes this item.While,based on the fact that the user has not assigned a rating to an item,the server can still infer that the user may be not interested in such items.To protect user’s rating behavior,in the PVB method and the UE_PVB method proposed in Section V,we introduce a parameter αn.This parameter is treated as the rating value of user n on item m,if user n has not rated the item m.The value of αncan be set in different ways.Here we consider the following five ways:
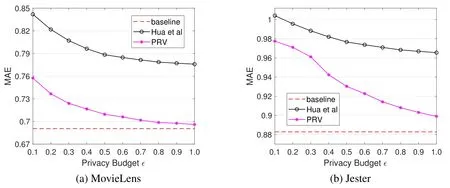
Figure 6.A comparison of the PRV method and Hua et al.’s method in terms of recommendation accuracy.
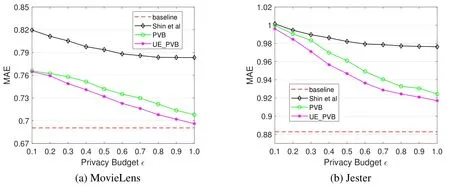
Figure 7.A comparison of the PVB method,the UE_PVB method and Shin et al.’s method in terms of recommendation accuracy.
·αn=Rand(X),namely αnis randomly selected from the set of all possible ratings;
·αn=sample(rn,m),namely αnis sampled from the distribution of the rated items for user n;
·αn=(rL+rH)/2,namely αnis set to the average of the lowest rating rLand the highest rating rH;
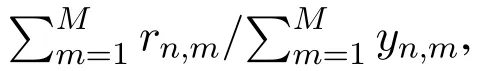
·αn=min(rn),namely αnis set to the minimum of the ratings assigned by user n.
We conduct a series of simulations to see the impact of αnon recommendation quality.For comparison propose,we also simulate the basic item-based CF algorithm(without αn).Simulation results are shown in figure 5.As we can see,the value of αnhas a significant influence on the recommendation quality.For MovieLens data,setting αnto the minimum of ratings can obtain the best result.This is because in Movie-Lens, if user n is interested in movie m, it is very likely that the user will choose to watch the movie and then assigns a rating to it.While,if user n has not rated movie m,it usually means that the user dislikes this movie.Thus,assigning the minimum of user n’s ratings to his/her unrated movies could better reflect user n’s preference.For Jester data,setting αnto the mediant can obtain the best result.This is because in Jester,if user n has not rated joke m,it usually means that the user n has never heard the joke m,so we cannot infer whether user n likes joke m.And assiging the same value(i.e.mediant)to all users’unrated items can weaken the negative effect of αnon recommendation.
6.3 Simulation Results
We conduct a series of simulations to evaluate the performance of the methods proposed in Section V.Table 1 shows the parameter settings in our simulations.We compare the PRV method with the method proposed by Hua et al.[31]which also provides LDP only for users’rating values.We also implement the method proposed by Shin et al.[32]and compare it with the proposed PVB method and the UE_PVB method.These three methods provide LDP for both users’rating values and rating behaviors.A baseline method which directly utilizes users’original ratings to make recommendations is also simulated.Given a dataset and a recommendation method,different settings of privacy budget ϵ are tested.The MAE is measured via 10-fold cross validation.The simulation results are present in figure 6 and figure 7.We can see that as the privacy budget increases,the recommendation quality of every proposed method becomes better.And as the privacy budget approaches to 1,the recommendation quality of all methods become closer to the baseline.We also find that the recommendation accuracy of the PRV method is always much better than Hua et al.’s method,and the PVB method and the UE_PVB method also perform better than Shin et al.’s method.In addition,we observe that the recommendation accuracy of the UE_PVB method is better than that of the PVB method.This coincides with the theoretical analysis presented in Section V.
To further demonstrate the performance of the proposed methods,we compute recall@5 under different settings of privacy budget.From the results shown in figure 8,we can see that for both datasets,the proposed PRV method performs much better than Hua et al.’s method when ϵ> 0.3.From the results shown in figure 9,we can find that both the PVB method and UE_PVB method outperform Shin et al.’s method when ϵ> 0.5.We can also find that the performance of the UE_PVB is better than the PVB method.Besides,figure 8 and figure 9 show that the performance on MovieLens is better than that on Jester.This is because LDP mechanisms are more effective when the number of users becomes larger.This proves that all the proposed methods can obtain good recommendation quality of Top-5 recommended items.
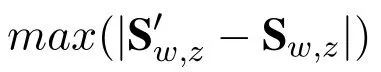
We also conduct a series of simulations to find out how the number of users affects the computation accuracy.We randomly sample N ≜{500,1000,3000,5000,8000,10000,20000,30000,50000,60000}users from MovieLens and sample N{500,1000,2000,3000,5000,8000,10000,12000,15000,20000}users from Jester respectively.Then,we evaluate||S′-S||maxand||S′-S||meancorresponding to different user sizes.From the results shown in figure 11,we can find that as the number of users increases,the computation error of all proposed methods decreases.For MovieLens data,as N approaches to 60,000,the mean computation error of every method falls below 0.1 and the maximum computation error falls below 0.3.And for Jester data,as N approaches to 20,000,the mean computation error of every method falls near 0 and the maximum computation error falls near 0.2.We can also find that the results on Jester are better than those on Movielens.This is because the Movielens data set is sparser than Jester.The simulation results prove that the proposed perturbation methods can lead to an accurate similarity matrix when the number of users is sufficiently large.
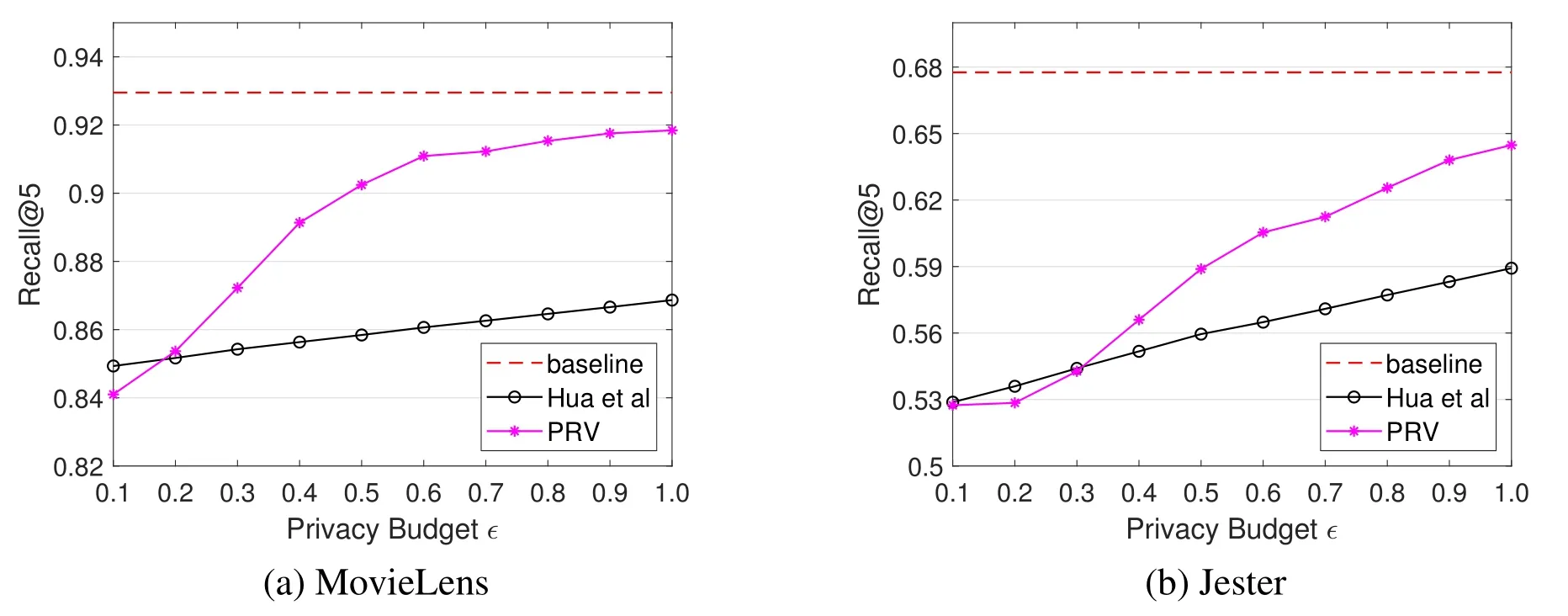
Figure 8.A comparison of the PRV method and Hua et al.’s method in terms of Recall@5.
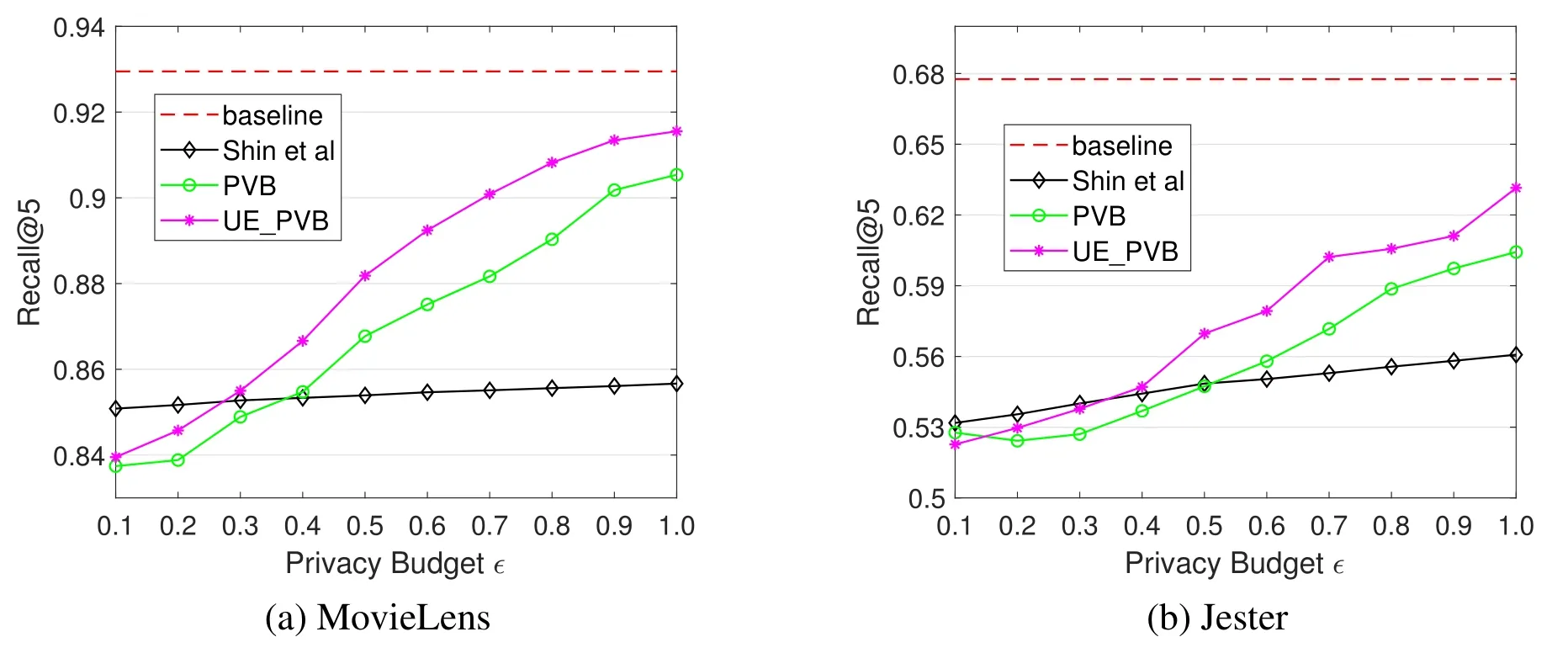
Figure 9.A comparison of the PVB method,the UE_PVB method and Shin et al.’s method in terms of Recall@5.
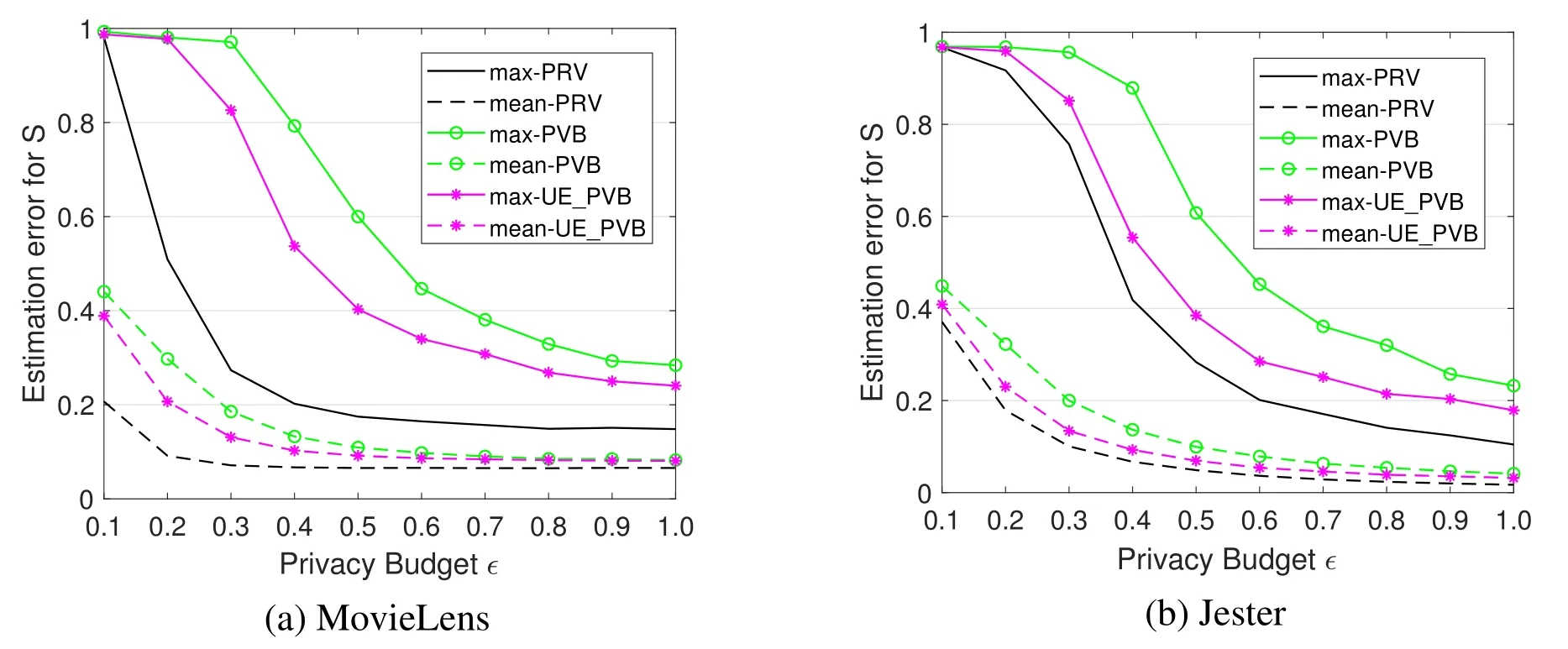
Figure 10.Estimation errors of similarity matrix evaluated on the private budget ϵ.The solid lines denote the results of||S′-S||max.The dotted lines denote the results of||S′-S||mean.
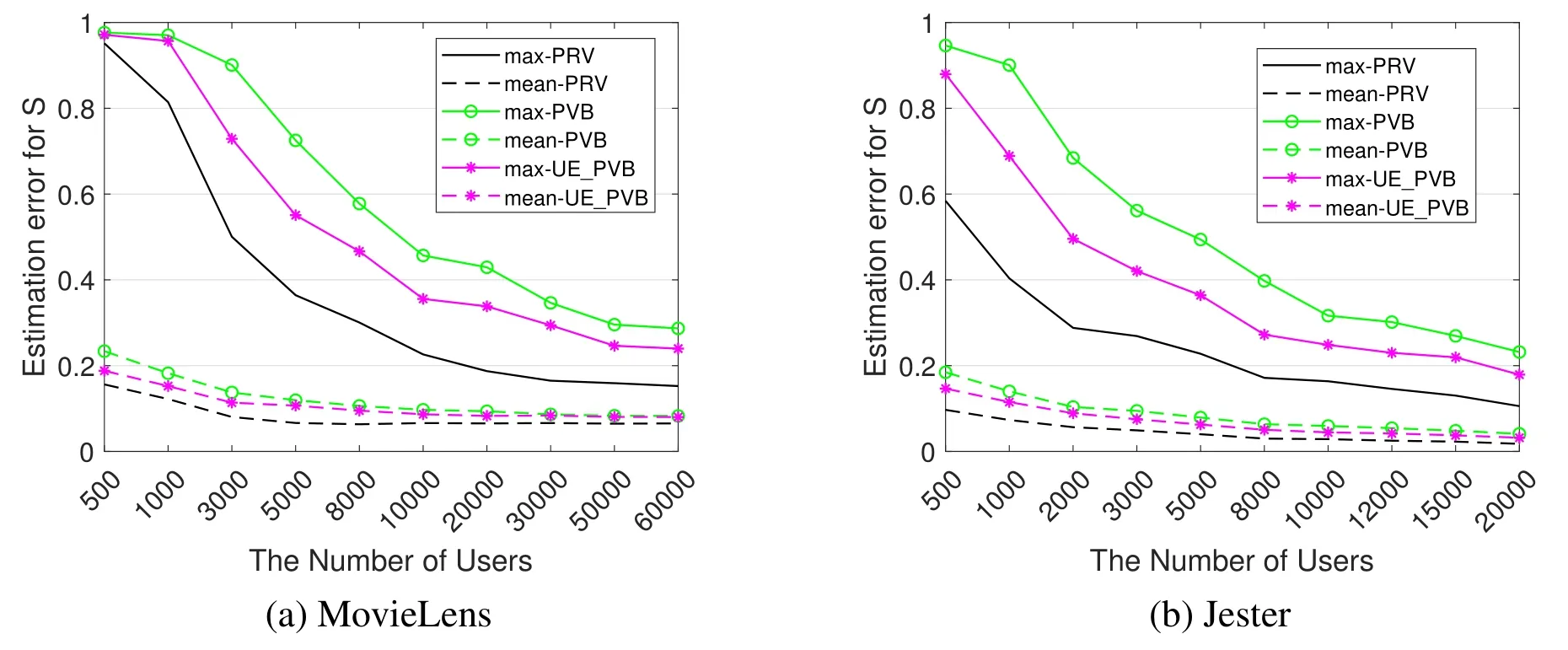
Figure 11.Estimation errors of similarity matrix evaluated on the number of users.The solid lines denote the results of||S′-S||max.The dotted lines denote the results of||S′-S||mean.
VII.CONCLUSION AND FUTURE WORKS
In this paper we have presented a recommendation framework which applies LDP techniques to itembased collabotative filtering.We first propose the PRV method which only protects users’rating values.Then,we present the PVB method which also protects users’rating behaviors.Considering the PVB method may provide excessive privacy protection,we propose the UE_PVB method which provides LDP only for users’rated items.By conducting a series of simulations on real-world data,we demonstrate that the proposed methods can not only provide strong privacy protection but also preserve the recommendation accuracy.
As we briefly addressed in the paper,the recommendation quality of the proposed methods heavily depends on the degree of data perturbation.Existing LDP mechanisms usually assume that the degree of perturbation is determined by the server.To give the users full control over their rating data,we plan to study how to obtain high-quality recommendation when each user determines his/her own degree of perturbation.
ACKNOWLEDGEMENT
This work is supported by National Natural Science Foundation of China(No.61871037).This work is also supported by Natural Science Foundation of Beijing(No.M21035).
APPENDIX
Proof of Theorem 6.First,according to Eq.(5),we can get
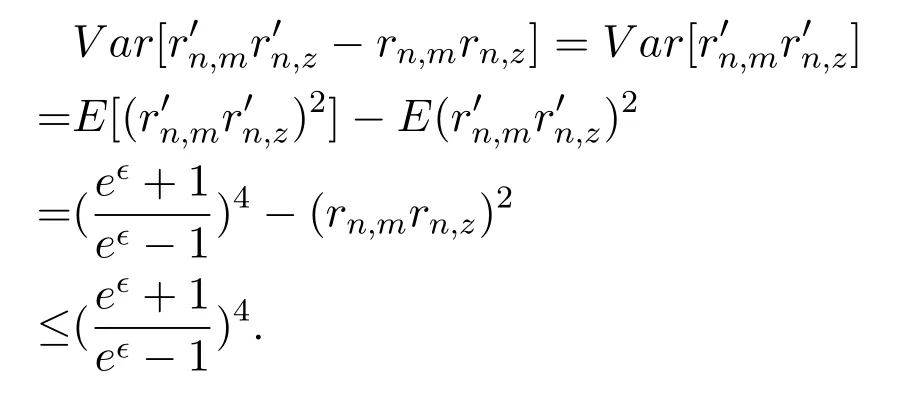

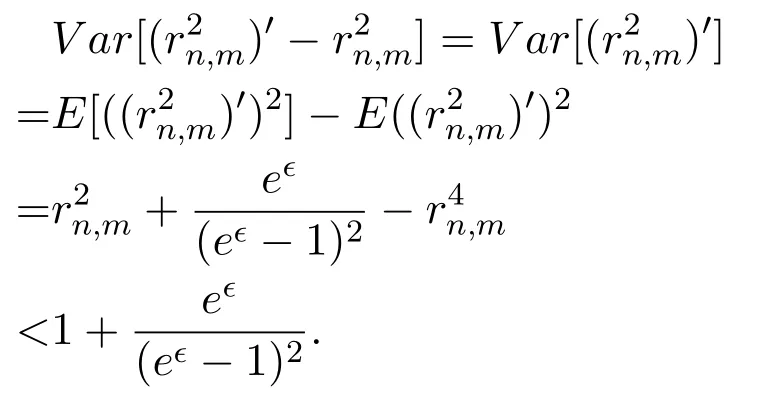
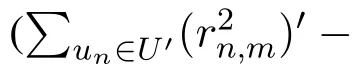
According to Chebyshev theorem,we know that∀0<α<1,there are
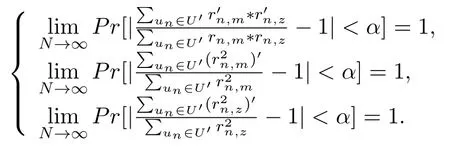
Then,we can get that∃N,when N>N,there are
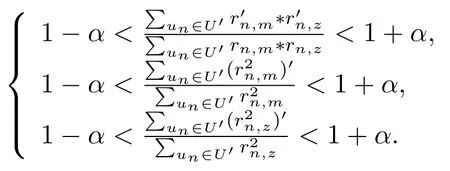
Then,we get

To measure the accuracy of similarity computation,we compute the ratio of the sim′(im,iz)to sim(im,iz)as follows

Then,based on the above analysis,we can get that when N>N,
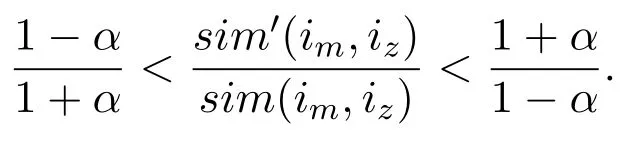
Then,we get
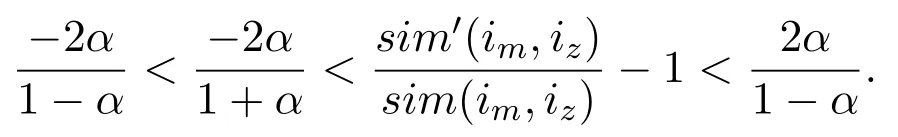
That is,
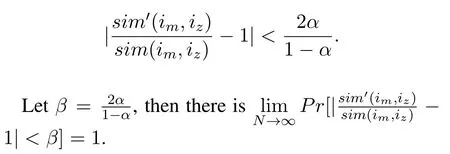
- China Communications的其它文章
- A Key Management Scheme Using(p,q)-Lucas Polynomials in Wireless Sensor Network
- Pilot Allocation Optimization Using Enhanced Salp Swarm Algorithm for Sparse Channel Estimation
- Put Others Before Itself:A Multi-Leader One-Follower Anti-Jamming Stackelberg Game Against Tracking Jammer
- DCGAN Based Spectrum Sensing Data Enhancement for Behavior Recognition in Self-Organized Communication Network
- On Treatment Patterns for Modeling Medical Treatment Processes in Clinical Practice Guidelines
- Hybrid Recommendation Based on Graph Embedding

