Pilot Allocation Optimization Using Enhanced Salp Swarm Algorithm for Sparse Channel Estimation

Ning Li,Kun Yao,Zhongliang Deng,Xiaohao Zhao,Jianchang Qin

School of Electronic Engineering,Beijing University of Posts and Telecommunications,Beijing 100876,China

Abstract:Pilot pattern has a significant effect on the performance of channel estimation based on compressed sensing.However,because of the influence of the number of subcarriers and pilots,the complexity of the enumeration method is computationally impractical.The meta-heuristic algorithm of the salp swarm algorithm(SSA)is employed to address this issue.Like most meta-heuristic algorithms,the SSA algorithm is prone to problems such as local optimal values and slow convergence.In this paper,we proposed the CWSSA to enhance the optimization efficiency and robustness by chaotic opposition-based learning strategy,adaptive weight factor,and increasing local search.Experiments show that the test results of the CWSSA on most benchmark functions are better than those of other meta-heuristic algorithms.Besides,the CWSSA algorithm is applied to pilot pattern optimization,and its results are better than other methods in terms of BER and MSE.

Keywords:OFDM channel estimation;CWSSA;compressed sensing;salp swarm algorithm;pilot allocation

I.INTRODUCTION

For wireless and satellite communications,the mobile channel is highly dynamic and random because of its varies according to the transmission environment.In the mobile communication channel,the wireless signal will experience a series of interference in the transmission process.After experiencing the complex environment such as scattering,refraction,multipath effect,and the comprehensive influence of mobile terminal on its transmission process,the signal presents irregularity.Because of the existence of the multipath effect,the phase,amplitude,and arrival time of the signal will be affected to a certain extent,and the signal between the receiver and the transmitter will change obviously.To reduce frequency-selective fading caused by the multipath effect,it is necessary to obtain accurate channel state information(CSI)through channel estimation for channel equalization of the receiver[1]and coherent demodulation[2].In channel estimation,the most common are pilot-base methods,such as least square(LS),minimum mean square error(MMSE)[3],and SVD[4].Recently,compressed sensing[5]has been introduced to deal with channel estimation in OFDM systems[6–16].Compared with traditional channel estimation methods,the method based on compressed sensing can take advantage of the inherent sparse characteristics of the wireless channel and provide accurate channel state information with fewer pilots and higher spectral efficiency.

In compressed sensing theory(CS),the signal reconstruction is often influenced by Restricted Isometry Property(RIP)[5],and it constructs a deterministic perception matrix to satisfy the RIP,to reconstruct the signal accurately.Because of the difficulty in calculating characteristics of RIP,there is no effective method to evaluate whether a certain matrix satisfies the RIP.In[17],a rigorous method of mutual coherence of the measurement matrix is proposed.After determining the number of OFDM subcarriers and the number of pilots,the pilot pattern satisfying RIP can be found through numerous calculations.Since the number of subcarriers is high,such processing cannot be completed in a short time,and it is easy to produce a”combination explosion”of the search.Therefore,this method of finding pilot patterns through calculation is impractical.A method based on discrete random approximation is proposed in[18],a cross-entropy optimization method is proposed in[19],what’s more,random sequential search and random parallel search methods are proposed in[20]to optimize pilot pattern.However,these methods above are difficult to satisfy in terms of time and convergence accuracy.

1.1 Related Work

In recent years,numerous algorithms have appeared in the field of swarm intelligence theory research,such as particle swarm optimization(PSO)[21–24],ant colony optimization(ACO)[25],artificial bee colony(ABC)[26],grey wolf optimizer(GWO)[27],bat algorithm(BA)[28],whale optimization algorithm(WOA)[29].It is worth mentioning that the study of pilot patterns in channel estimation can be regarded as an optimization problem.In[30–34],the adaptive GA,GWO,EDA,PSO,and PSO-GA optimization algorithms were adopted to solve the optimization problem of the pilot pattern.In[35]proposed a method of cyclic difference set.

In 2017,Mirjalili et al.proposed a new swarm intelligent optimization algorithm called the salp swarm algorithm(SSA)[36],which simulates and models the gregarious behavior of salp.Compared with other algorithms,the SSA algorithm has the advantages of fewer control parameters simple implementation,etc.These remarks make the SSA algorithm theoretically and potentially able to solve single-objective optimization problems with unknown search spaces.The adaptive mechanism of the SSA algorithm allows it to avoid local solutions and eventually finds an accurate estimation of the best solution obtained during optimization.

1.2 Our Contribution

In this paper,we propose a new pilot pattern optimization method based on the CWSSA for sparse channel estimation in OFDM systems.The algorithm in this paper improved the SSA algorithm based on chaotic opposition learning strategy,adaptive weight factor,and local search,which can avoid premature phenomena and break away from the local optimum by a higher probability to achieve an overall optimization.Then,the algorithm is proposed for pilot pattern optimization in OFDM systems for sparse channel estimation.Simulation results show that the CWSSA has not only superior performance in test functions but also higher efficiency in the pilot pattern optimized than other algorithms.

It organizes the rest of this paper as follows.In the second part,we analyze the channel estimation model of OFDM.Part three mainly introduces the SSA algorithm,the proposed CWSSA,and its application in pilot pattern optimization.Simulations and results of the considered methods are given and analyzed in the fourth part.Finally,the conclusion is given in Section V.

II.SYSTEM MODEL AND PROBLEM FORMULATION

Assuming the OFDM system has N subcarriers,where P subcarriers are reserved for the transmission of pilot symbols.xi(i=1,2,3...,N)is the time domain information transmitted by the transmitter,including data symbols and pilot symbols,where pilot symbols are represented as k={k1,k2,...,kP}(1≤k1＜k2＜...＜kP≤N),the received signal in time domain yi(i=1,2,3...N)can be obtained at the receiver.Therefore,the signal transmission model can be expressed as

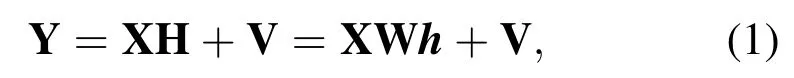
where X=diag(x1,x2,...,xN)is the N×N dimension OFDM signal matrix formed by diagonalization of N subcarriers,h=[h1,h2,...hL]Tis the channel impulse response(CIR),W is the N×L dimensional Fourier transform matrix,and V is the additive white Gaussian noise term.Then,the transmission model of pilot symbols can be expressed as

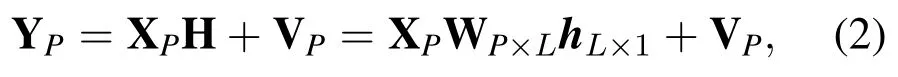
where XP=diag(x1,x2,...,xN),WP×Lis the partial Fourier transform matrix.Denote the measurement matrix

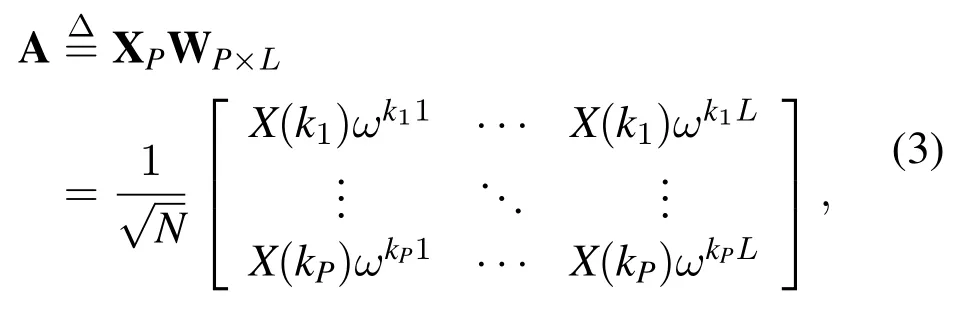
where ω=e-j2π/N.Then,the transmission model of OFDM signal can be expressed as

From Eq.(4),Observation YPand measurement matrix A are known at the receiver.Therefore,we can recover channel matrix h with high probability through compressed sensing algorithms such as orthogonal matching pursuit(OMP)[37],subspace pursuit(SP)[38],and compressive sampling matching pursuit(CoSaMP)[39],etc.Therefore,in this case,the channel estimation problem of OFDM systems can be transformed into the design of the measurement matrix under specific conditions.

According to the theory of compressed sensing(CS)[5],the better the RIP property of the measurement matrix A is,the higher the probability of recovery the channel response matrix h can be in theory.However,it is difficult to calculate whether the measurement matrix satisfies the RIP condition because of the high computational complexity.Another method of studying the RIP criterion,namely the mutual coherence of the measurement matrix,is given in[17].The smaller the mutual coherence coefficient of the sensing matrix is,the better the RIP criterion is.We express the mutual coherence coefficient of the measurement matrix as follows

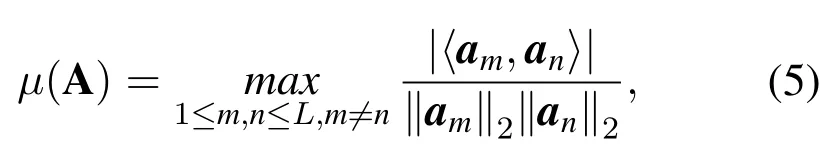
where amand anare the normalized column vectors of A,‖·‖2denotes the 2-norm.It can be obtained by combining Eq.(3)and Eq.(5)

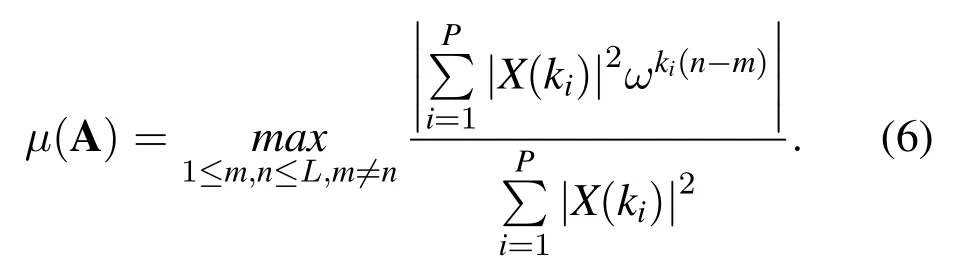
From Eq.(6),we find that the mutual coherence of the measurement matrix is determined by the pilot power and the pilot allocation positions.In this paper,we only focus on the effect of pilot allocation positions for channel estimation so that we take|X(k1)|=|X(k2)|=···=|X(kP)|=1.Then Eq.(6),can be written as

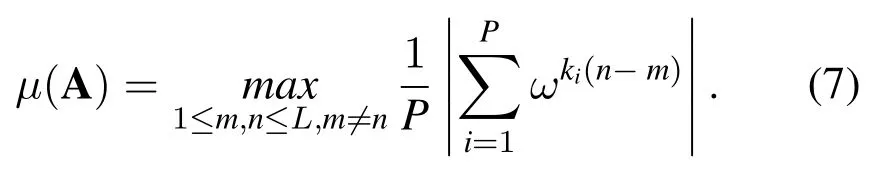
As mentioned in[17],we aim to minimize the mutual coherence of the sensing matrix A in searching for the optimal pilot pattern to ensure that the CIR vector h can be recovered with a high probability[32].Therefore,the problem of pilot pattern optimization can be defined as

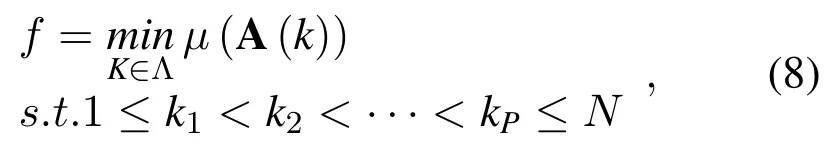
where Λ is a set composed of all the candidate pilot patterns,and the Λ is C(N,P).As mentioned,it is intractable to exhaustively search all possible pilot patterns from the set Λ.Consequently,finding a superior performance way to obtain pilot pattern is a question that is worth studying.

III.THE SOLUTION PROPOSED IN THIS PAPER

Salp swarm algorithm(SSA)[36]is a new heuristic intelligent optimization algorithm proposed by Mirjalili et al.in 2017.It has the advantages of simple implementation,few parameters,and low calculation cost.In terms of the accuracy and convergence speed of the optimal solution,SSA is superior to other algorithms such as PSO[21]and GA[40].Up to now,heuristic intelligent optimization algorithm has been widely used in many fields providing a new thought for optimization problem in Eq.(8).In this part,we proposed an enhanced SSA algorithm called the CWSSA at first.And then,the CWSSA is used to optimize pilot allocation for channel estimation in OFDM systems.

3.1 Mathematical Model For Salp Chains[36]

For the mathematical model of the salp chain,the population is divided into two groups:leader and followers.The leader is the salp at the front of the food chain,while we consider the rest as followers.As the name of these salps suggests,the leader guides swarm,and the followers follow each other.

The position of the leader is updated according to the location of the food source so that it is always in the vicinity of the food source for exploration and exploitation.Its position is updated randomly by

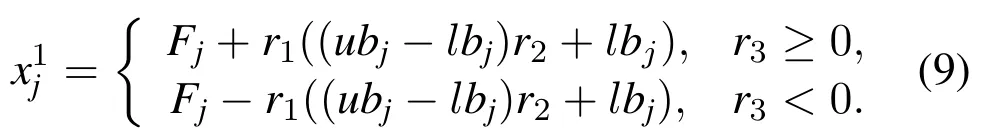
where l is the number of current iterations,L is the maximum number of iterations.

The parameters r2and r3are uniformly generated random numbers in the interval[0,1],which determine the next position in the jth dimension to be positive or negative,and the length of the movement.These parameters enhance the randomness of the leader movement,global search ability,and individual diversity.

The position of the followers is updated according to Newton’s laws of motion

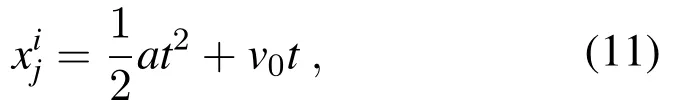
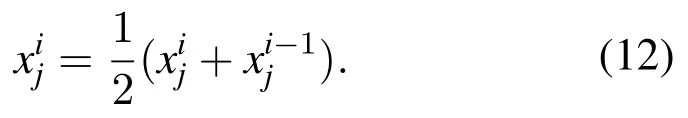
When solving the optimization problem,the SSA firstly randomly initializes the salp position within a limited range,calculates the fitness value to find the optimal salp,and allocates the optimal salp position to the food source.The leader and the followers updated their positions according to Eq.(9)and Eq.(12),respectively.Because the global optimal solution of the optimization problem is unknown,it can only use the current optimal position as the position of the food source and constantly follow the new food source according to the optimal location in the search process.The best position of the food source is recorded,and even if the position of the salps population deteriorates,it will not lose the best position information.

3.2 Proposed CWSSA

Unfortunately,in practical issues,the SSA algorithm still has the possibility of trapping into the local optimal solution and a slow rate of convergence.In order to solve the above problems,this paper proposed the CWSSA.

3.2.1 Chaotic Opposition-based Learning

Generally speaking,the distribution of the initial population directly affects the convergence speed,optimization accuracy,and stability of the SSA algorithm.In the initialization phase, without any guidance from prior knowledge,the initial population generated randomly will have great uncertainty.In the case of a limited number of individuals and iterations,it may not traverse the entire search space completely,which makes the algorithm easily fall into the situation of the local optimal solution.

Chaos is a universal phenomenon in nonlinear systems.It can traverse all the states in a certain range without repetition.The sequence itself has the characteristics of randomness,ergodic property,and regularity[41],and the initial population generated by it has a good diversity so it can better traverse the whole solution space.If the position of the initial population is close to the global optimal solution of the position,then the algorithm of the ability to obtain the optimal solution and the convergence speed will be the best,but the initial population generated randomly is basically not ideal,so we need to make them as maximum as possible to get good initial population distribution.

In this paper,we adopted the strategy of chaotic opposition-based learning(OBL)[42]to initialize the population.Compared with the randomly distributed population,the improved initial population distribution expanded the search range of salps,increased the diversity of population locations,and improved the global optimization ability of the algorithm.The expression of circle chaotic mapping is as follows

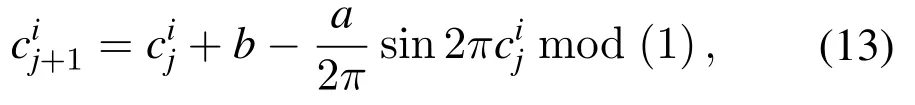
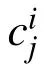
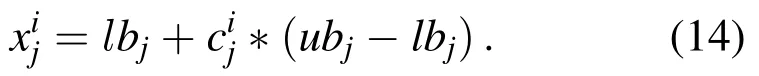
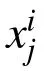
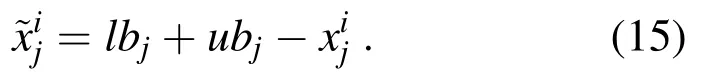
Adding opposition-based learning in the population initialization can make the function of chaos more powerful.By comparing the fitness values of the initial positions of the population before and after a chaotic local search,it can select a better individual position to improve the performance of the algorithm in terms of convergence speed.The fitness value of the current population and its opposite in the search space will be calculated by

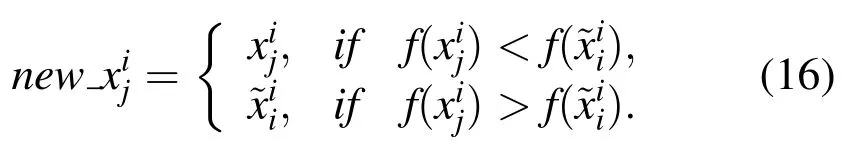
where f(·)is the fitness function.

3.2.2 Adaptive Weighting Factor

According to the position update formula of followers in Eq.(12),we find that the position of the ith salp will be updated according to the position of the ith and i-1th salp.In this case,if the position of the followers is trapped in a local optimum,the algorithm will be stagnated and unable to be further optimized.

To avoid the occurrence of local optimum situation,and improve the population’s strong iteration ability at the initial iteration stage and a strong local optimization ability in the later iteration stage,the weight factor is introduced as shown in Eq.(17)

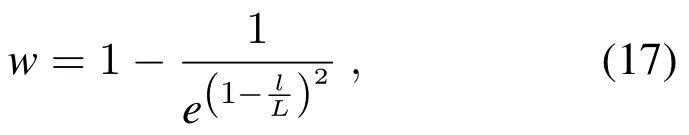
where l is the number of current iterations,L is the maximum number of iterations.Then the position of the followers changed as shown in Eq.(18)

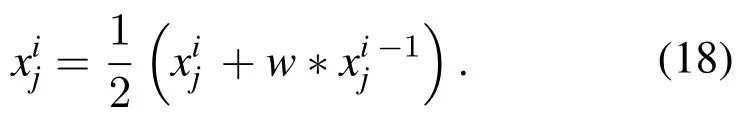
The dynamic change of weight factor makes salps have different exploration and exploitation abilities in different stages.At the beginning of the iteration,a larger weight factor is beneficial to the exploration ability of the algorithm.In the later stage of iteration,a smaller weight factor is helpful to the exploitation ability of the algorithm.

3.2.3 Local Search

In actual cases,the heuristic algorithm will often fall into the local optimal solution of the shortcomings,to make the SSA algorithm jump out of the local optimal solution,we use the idea of simulated annealing algorithm(SA)[43]and introduce random factors to accept a solution with a certain probability that is worse than the current value.Therefore,it is possible to break away from the local optimum by a greater probability to achieve an overall optimization.The main idea is to use the SA algorithm to add a supplementary search process,named local search,after determining the optimal solution of the population.According to the Metropolis criterion,as shown in Eq.(19),it accepts the movement of the new individual with a certain probability. With time, it gradually approaches the global optimal solution. By giving the search process a time-varying and eventually zero probability mutation,it avoids falling into a local minimum and achieves the global optimum.

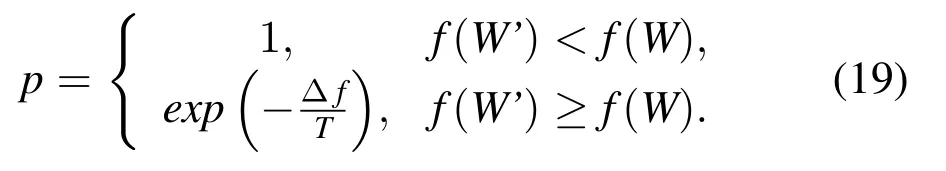
where T is the temperature.

3.3 CWSSA-Based Pilot Pattern Optimization

IV.SIMULATION RESULTS AND ANALYSIS

Table 1.CEC2005 classic benchmark function.

In this part,we mainly demonstrate the superior performance of the proposed algorithm in benchmark function and channel estimation by simulation.

4.1 Benchmark Testing For CWSSA

We selected 12 functions from CEC2005 benchmark functions to compare the performance of the proposed algorithm with SSA,PSO,GWO,ABC,and other classical algorithms.These test functions can be mainly divided into two types:(1)low-dimensional single-mode functions(F1～F7)are used to test the optimization accuracy and convergence speed of the algorithm,and there is only one extreme value in the search area for these functions,(2)high-dimensional multi-mode functions(F8～F12)are used to test the optimization ability of the algorithm and the ability to avoid local optimization.These functions have multiple extremum values in the specified search area.The mathematical formulas and related parameters of these functions are shown in Table 1,where Range and Fminrespectively represent the search boundary range and the theoretical optimal value of each test function.

In order to avoid the influence of other factors on the experimental results,algorithm parameters are shown in Table 2.Each test function is run 30 times,and its mean value and standard deviation,as well as the optimal value and the worst value are shown in Table 3,Table 4.For each standard function,the optimal value is obtained by different algorithms are highlighted in bold.It is easy to find that the algorithm proposed in this paper has strong competitiveness among the 12 test functions,especially when the function reaches the theoretical optimal value is 0.On the one hand,the CWSSA shows better optimization results than the others for the unimodal functions from to in Table 3 except for in which the GWO algorithm gets the best solution.On the other hand,the CWSSA shows better optimization results than others for the unimodal functions from to in Table 4.Especially,the proposed CWSSA achieves the theoretical optimal value of zero for F9and F11functions.

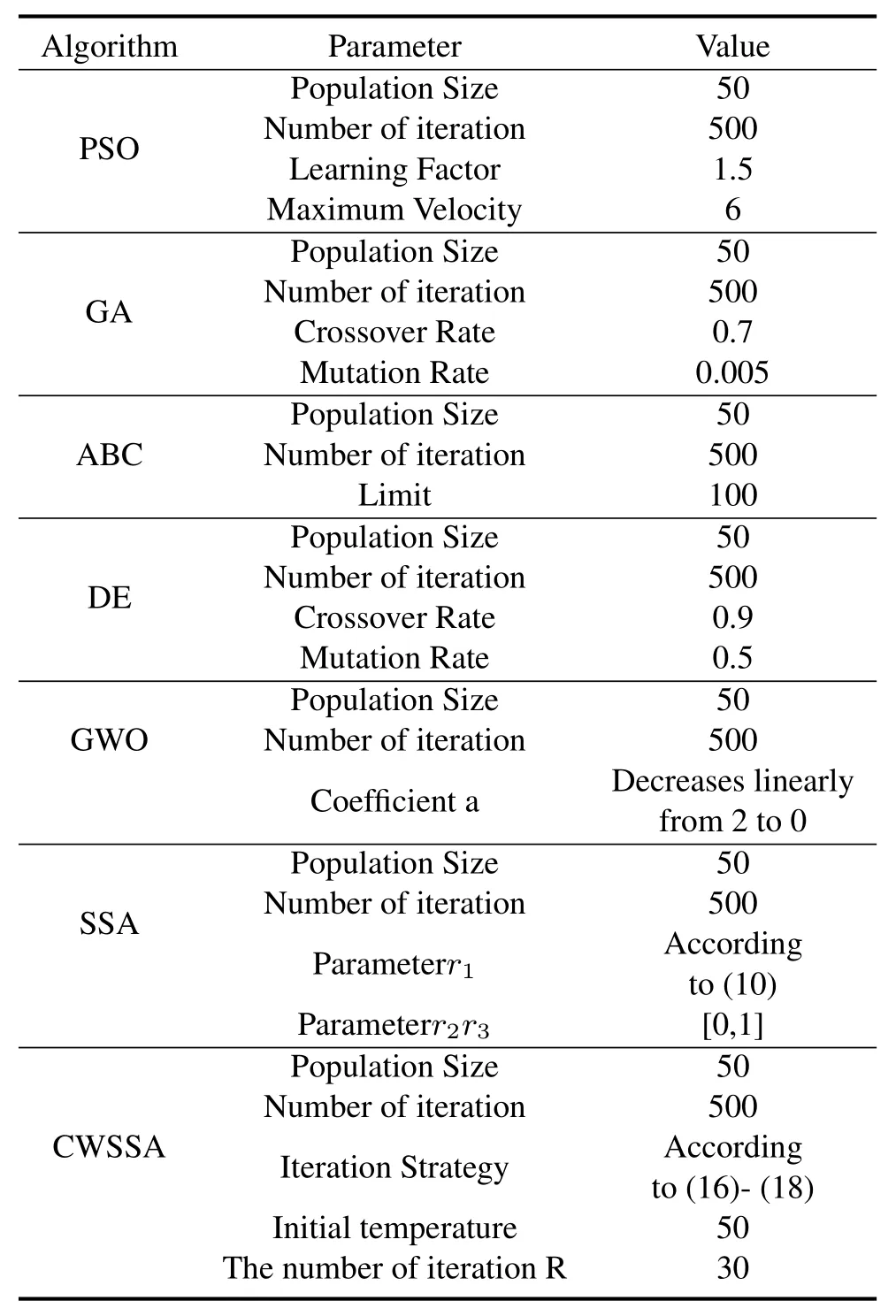
Table 2.Simulation parameters for optimization algorithms.

4.2 Performance For Channel Estimation

4.2.1 Obtain Pilot Patterns

In this section,we will verify the proposed method through numerical simulation experiments.Numerical experiments include mean square error(MSE)and system bit error rate(BER)for channel estimation.In addition,our proposed pilot design method based on the CWSSA is adopted to the OFDM system and compared with the equispaced,random,PSO,GWO,EDA,and SSA algorithm based pilot strategies regarding BER and MSE.

We consider a sparse channel with L=50,where K nonzero taps randomly distributed in[1,50]are independently distributed complex Gaussian distribution.The other simulation parameters about the OFDM system are demonstrated in Table 5,and other simulation parameters about optimization algorithms are shown in Table 6.

In Figure 1,we compare the convergence curves of the objective functions of several algorithms where the number of pilots P=16 and P=24.We can find that in different conditions,when the maximum number of iterations is reached,the CWSSA we proposed can always achieve the best performance.This is because we have increased the diversity of the initial population and expanded the search range so that the algorithm has better exploration and exploitation capabilities.Along with the increasing of iteration times,the PSO,GWO,and EDA algorithms have low efficiency because they are gradually appearing premature phenomena and tend to be trapped by local optimizations.The CWSSA includes adaptive weighting factor and local search during the running time,which can be useful to improve the ability of the algorithm in breaking away from the local optimum by a higher probability to achieve an overall optimization.

From Table 7,we can find that the fitness values of the PSO,GWO,EDA,SSA,and CWSSA are lower than the equispaced with 1.000 and random with 0.74298,where the value of CWSSA is 0.31727 better than PSO with 0.35258,GWO with 0.34753,EDA with 0.33635 and SSA with 0.32878.And in Table 8,we can find that the CWSSA still has the minimum with 0.23205,the equispaced has the maximum with 0.91220.The results showed that the CWSSA had proved its superiority over other algorithms in terms of pilot pattern optimization.

4.2.2 MSE And BER Of Channel Estimate

In this subsection,we evaluate the sparse channel estimation based on MSE of channel estimates and BER of systems and consider two cases where K=5,P=16,N=256 and K=6,P=24,N=512.We run 2000 simulations for each SNR and the simulation results of MSE and BER are shown in Figure 2 and Figure 3.specifically,from Figure 3,BER of the equispaced,random,PSO,GWO,EDA,and CWSSA method are 1.769×10-1,2.725×10-2,1.657×10-2,1.373×10-2,1.024×10-2,5.85×10-3,1.378×10-3at 30 dB SNR respectively.MSE of the equispaced,random,PSO,GWO,EDA and CWSSA method are 2.94×10-1,2.57×10-2,1.159×10-2,5.559×10-3,3.383×10-3,1.896×10-3,5.324×10-4at 30 dB SNR respectively.It can be seen that our proposed CWSSA is superior to other pilot allocations optimization algorithms to obtain the best BER and MSE.It is obvious that the equispaced method shows the worst performance.With the increase of the SNR,the BER and MSE remain unchanged.From Figure 2,we can still find that the CWSSA has the best performance.

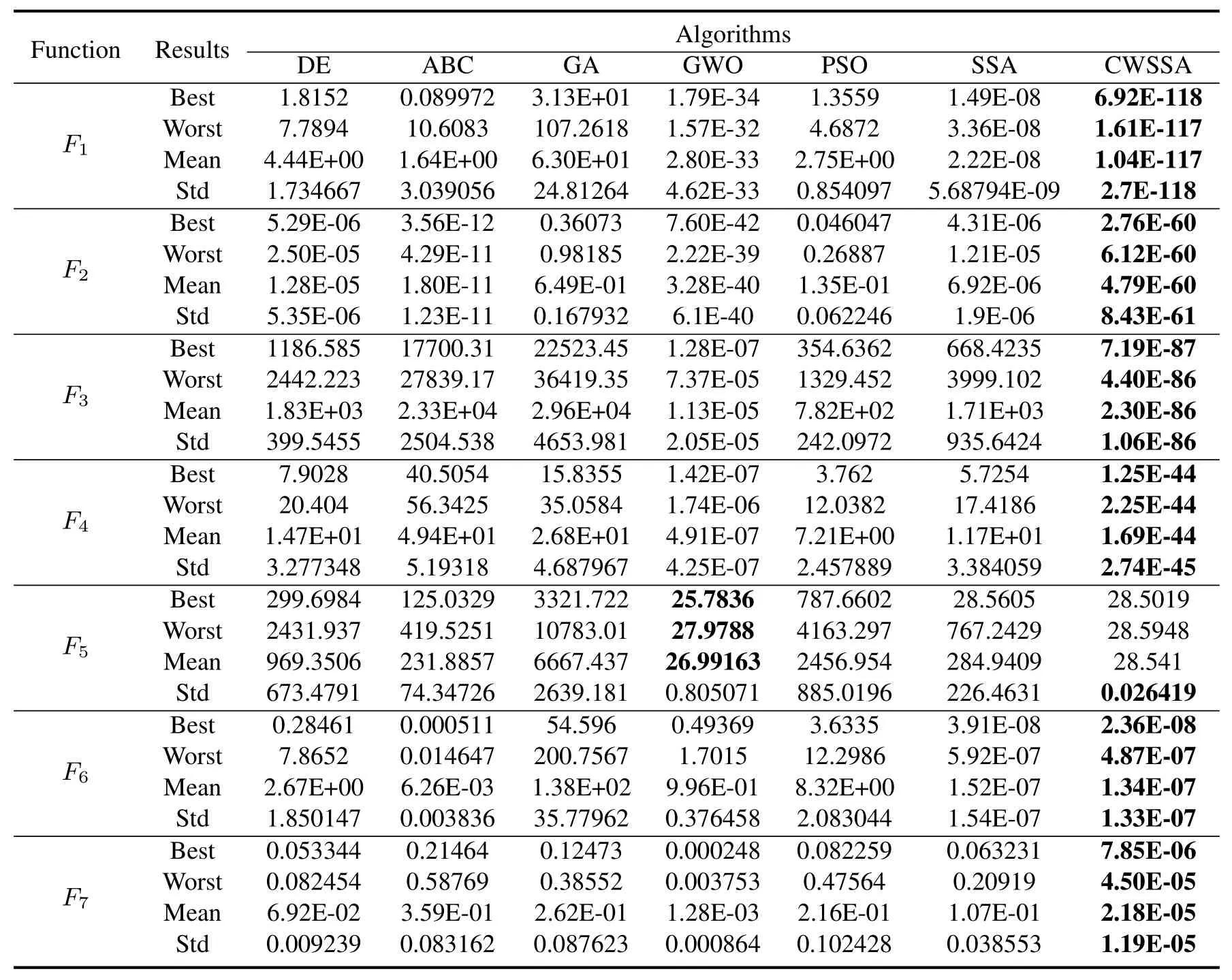
Table 3.Results of benchmark function F1to F7.

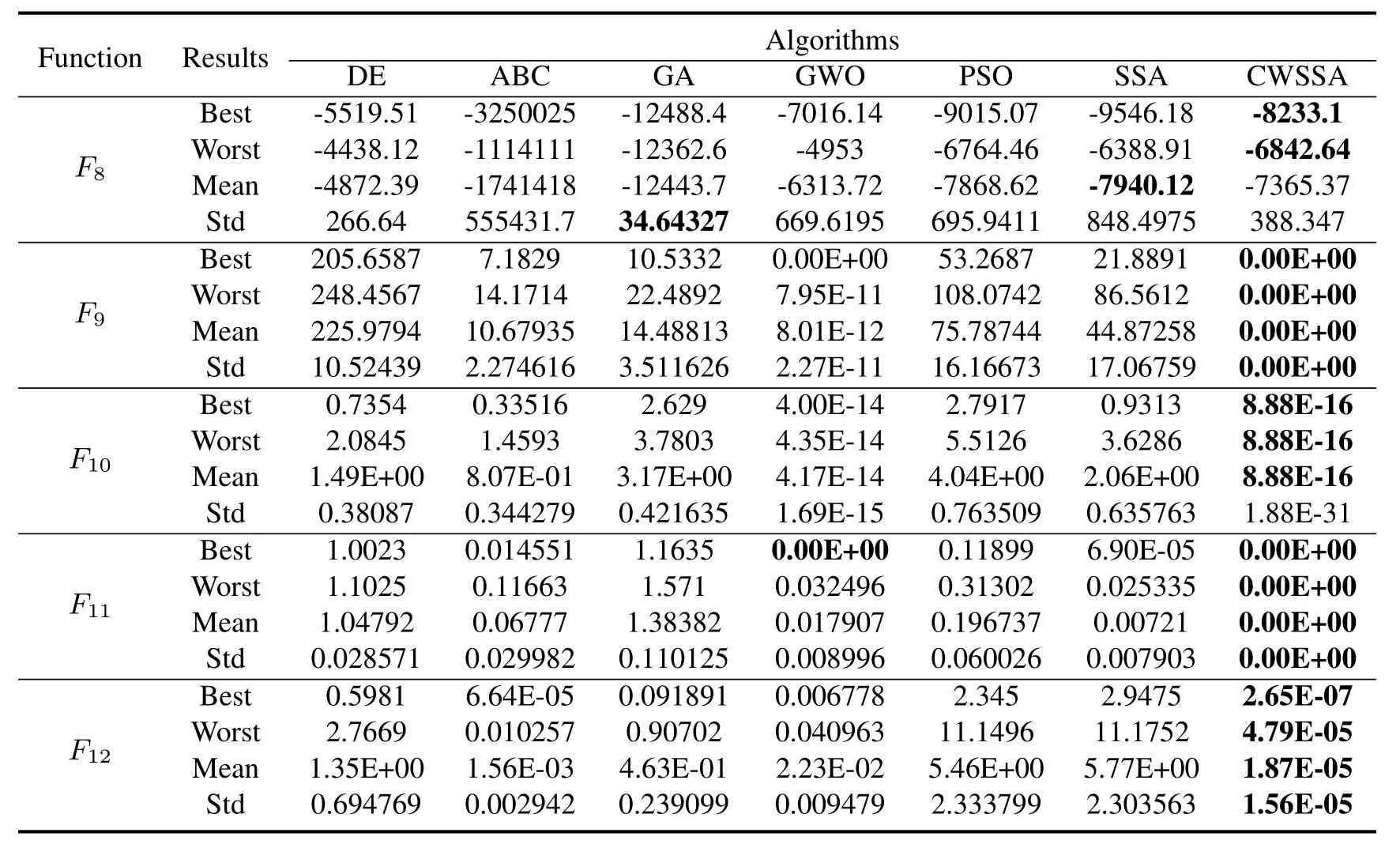
Table 4.Results of benchmark function F8to F12.

Table 5.Simulation parameters for OFDM system.

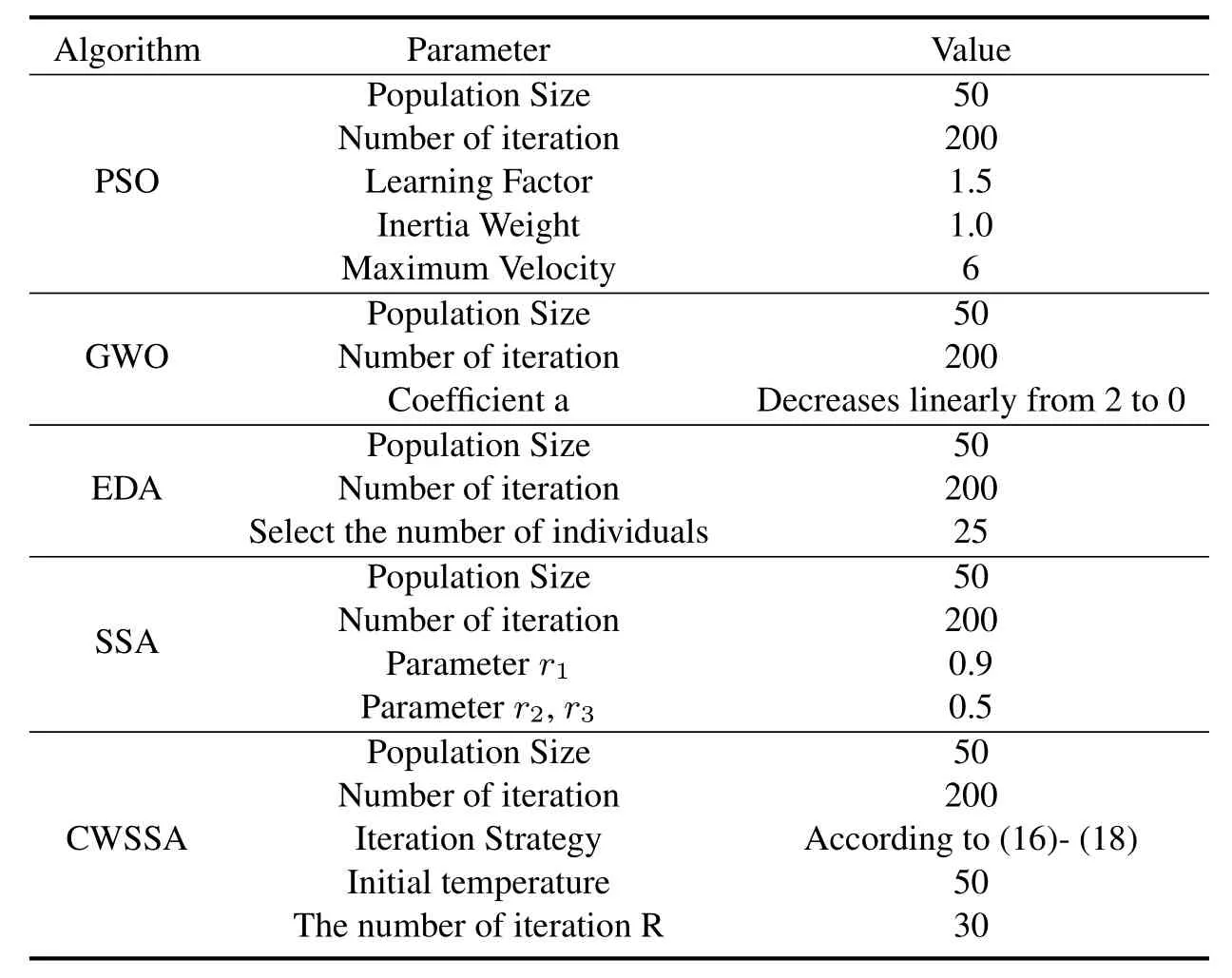
Table 6.Simulation parameters for optimization algorithms.

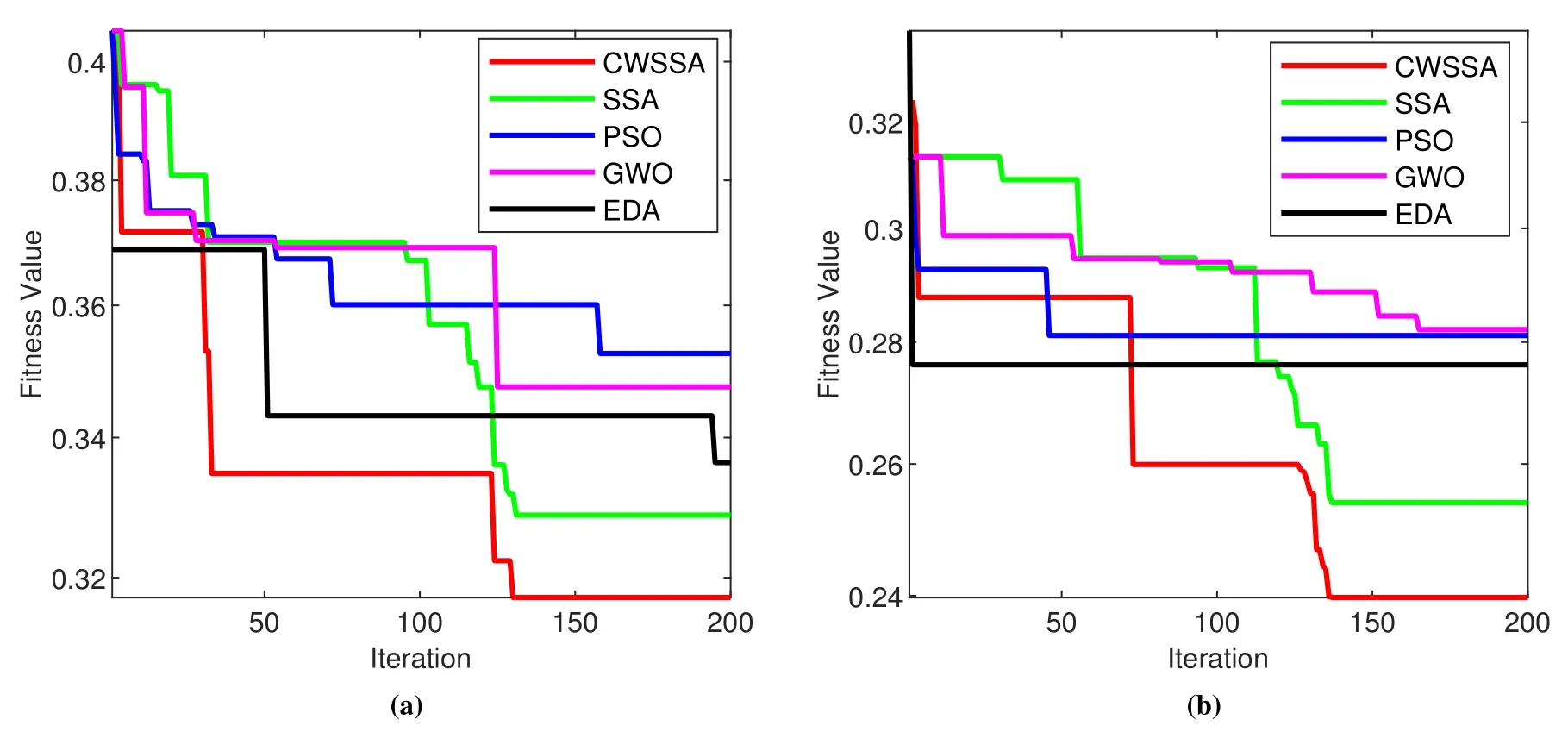
Figure 1.Convergence curves of various optimization algorithms in different pilots.(a)P=16.(b)P=24.

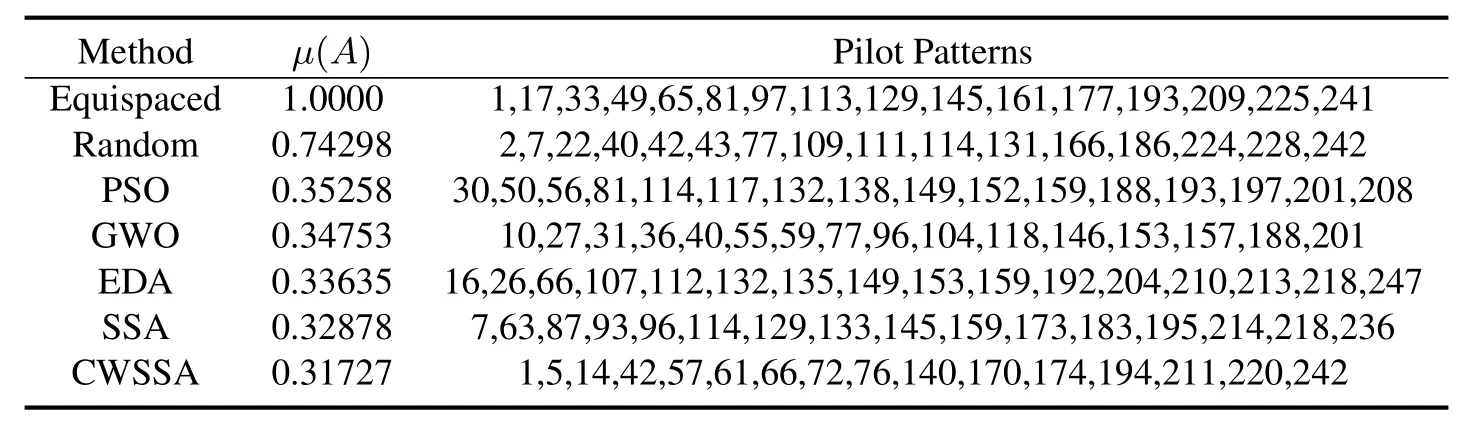
Table 7.Pilot patterns,P=16.

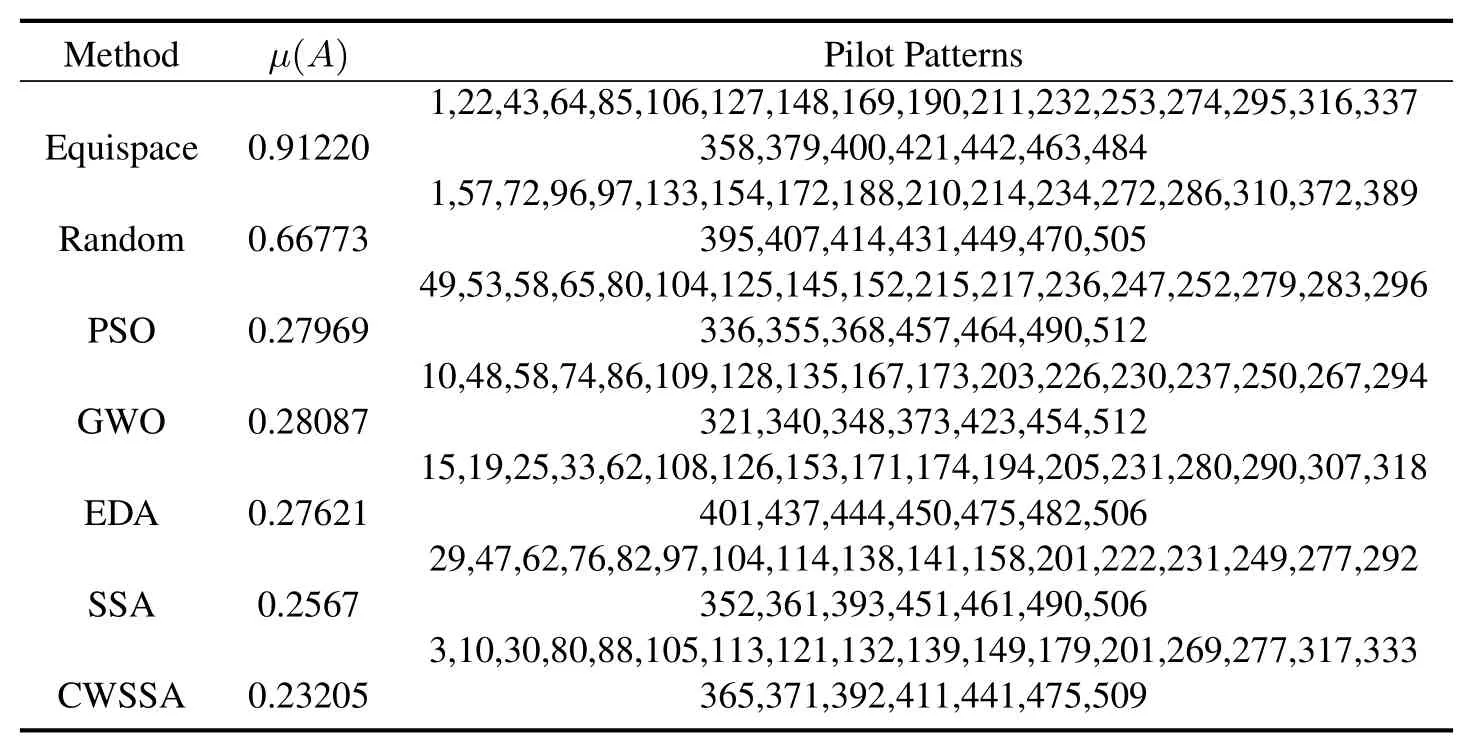
Table 8.Pilot patterns,P=24.

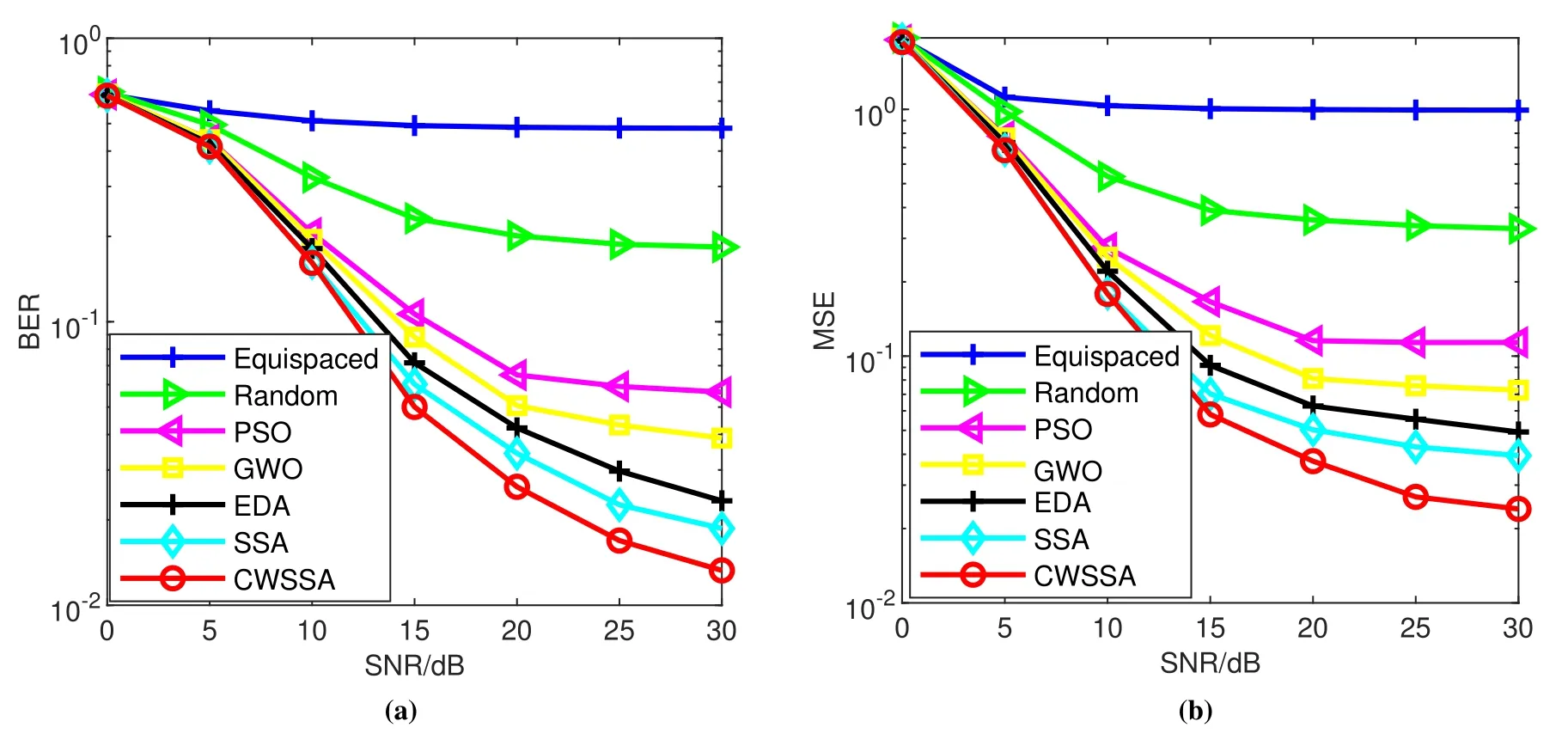
Figure 2.Comparison of BER and MSE in different pilot allocation methods,P=16.

4.2.3 Computational Complexity Analysis

The computational complexity of the optimization algorithm is a key index to evaluate the running time of the algorithm.The computational complexity can be defined according to the structure of the algorithm.In the SSA algorithm,the computational complexity is mainly reflected in the number of salps,the number of variables(dimension),and the maximum number of iterations.By analyzing the steps of the SSA algorithm,we know the computational complexity is O(t(d*n+Cof*n))where t shows the number of iterations,d is the number of variables(dimension),n is the number of solutions,and Cof indicates the cost of the objective function.The CWSSA adds chaotic opposition-based learning strategy and local search during the population initialization phase and iterative optimization process,respectively.First of all,the complexity order of population initialization is O(t(d*n+Cof*n)),and the time complexity of the optimization iteration process is O(t(d*(n*R)+Cof*n)).According to the above two parts,the time complexity of the CWSSA is O(t(d*(n*R)+Cof*n)),where R is the maximum iteration number of local search.Although we have increased the complexity of the algorithm,from the perspective of the optimal value obtained by the algorithm,the effect of the CWSSA is much better than the original SSA algorithm.

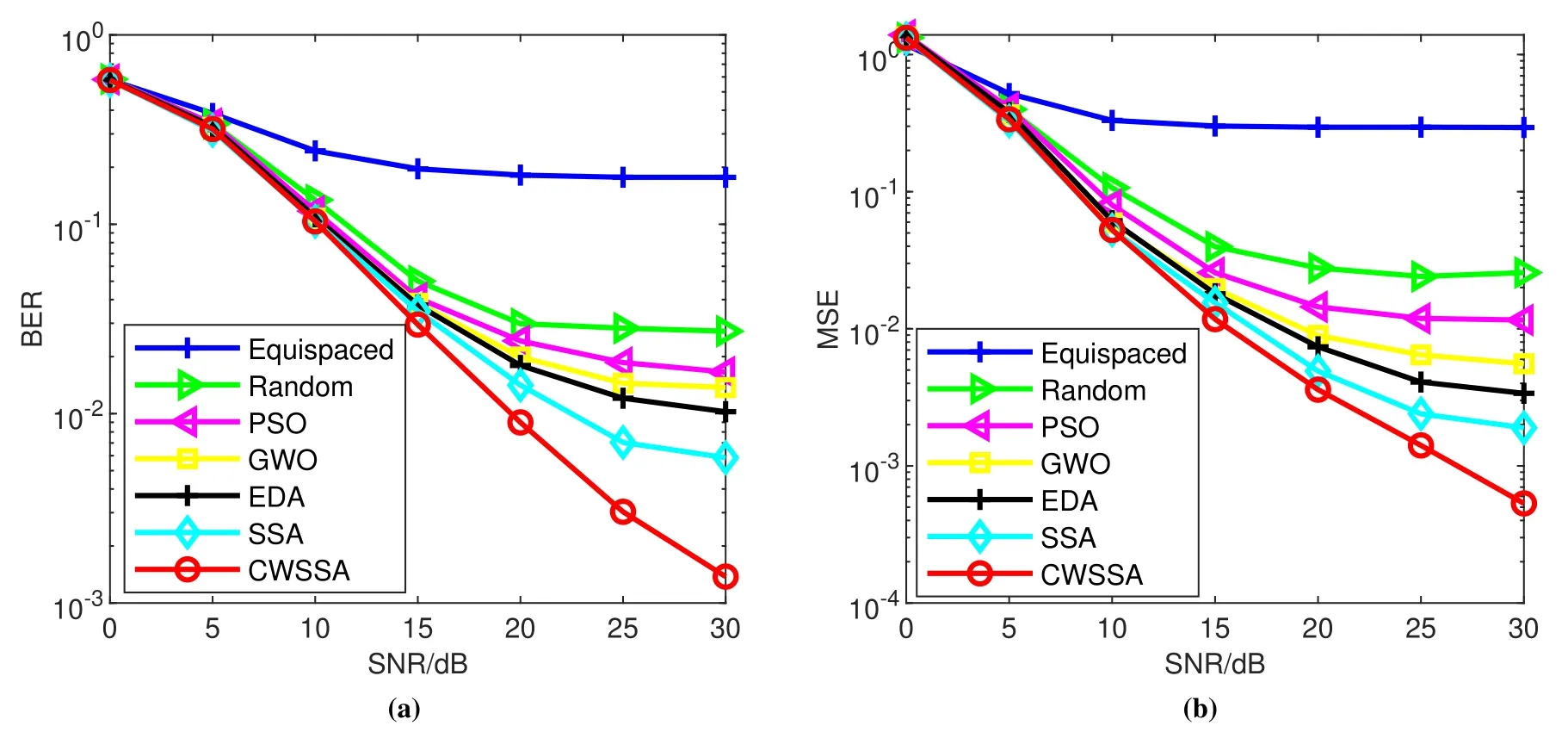
Figure 3.Comparison of BER and MSE in different pilot allocation methods,P=24.

V.CONCLUSIONS

Based on the research of the pilot pattern problem,this paper put forward the idea of applying the SSA algorithm to the optimization of the pilot pattern.However,some defects such as slow convergence rate and getting into a local minimum in the SSA algorithm,an improved SSA algorithm is proposed to solve the global optimization problem.By introducing the chaotic opposition-based learning strategy,the algorithm has a good sameness through the initial population,so it can traverse the whole solution space better.The adaptive weighting factor is used to enable the CWSSA to have different exploration and development capabilities in different stages.Finally,by introducing the simulated annealing algorithm(SA)and adding the supplementary search process,the local optimal value can be avoided.Then the CWSSA is applied to search for the pilot pattern with minimum mutual coherence by combining the theory of compressed sensing with channel estimation.The simulation results show that our paper provides an obvious superiority over the equispaced,random,PSO,GWO,EDA,and SSA based pilot design techniques not only in high MSE and BER performances but also in different subcarriers.