A Key Management Scheme Using(p,q)-Lucas Polynomials in Wireless Sensor Network

Amit Kumar Gautam,Rakesh Kumar

Madan Mohan Malaviya University of Technology,Gorakhpur-273001,India

Abstract:Wireless Sensor Network(WSN)has witnessed an unpredictable growth for the last few decades.It has many applications in various critical sectors such as real-time monitoring of nuclear power plant,disaster management,environment,military area etc.However,due to the distributed and remote deployment of sensor nodes in such networks,they are highly vulnerable to different security threats.The sensor network always needs a proficient key management scheme to secure data because of resourceconstrained nodes.Existing polynomial based key management schemes are simple,but the computational complexity is a big issue.Lucas polynomials,Fibonacci polynomials,Chebychev polynomials are used in Engineering,Physics,Combinatory and Numerical analysis etc.In this paper,we propose a key management scheme using(p,q)-Lucas polynomial to improve the security of WSN.In(p,q)-Lucas polynomial,p represents a random base number while q represents a substitute value of x in the polynomial.The value of p is unique,and q is different according to communication between nodes.Analysis of the proposed method on several parameters such as computational overhead,efficiency and storage cost have been performed and compared with existing related schemes.The analysis demonstrates that the proposed(p,q)-Lucas polynomial based key management scheme outperforms over other polynomials in terms of the number of keys used and efficiency.

Keywords:key management;lucas polynomial;WSN security;pairwise key distribution;key generation;hierarchical key management

I.INTRODUCTION

Wireless sensor network finds its application widely in both the industrial and commercial fields such as the health care system,habitat,and environmental monitoring,transportation system,military system,industry etc.[1].WSN has gained a significant amount of attraction from researchers as well as industrial communities.It supports mobile communication requirements,like in industrial electronics,sensors can be used for collecting and observing the data.The job of sensors is to find out environmental events and transmit that data to the sink node so that further processing can be done.Since the environmental events do not happen often,thus,the rate of data traffic between the sink node and the sensors is usually low,thereby it’s suitable to apply wireless sensor communication.A WSN has certain characteristics such as the ability to cope with sensor node failures,dynamic arrangement of nodes,short duty sequence,low energy,multi-hop communication and self-con figure sensors.Sensor nodes might be similar or dissimilar and either fixed or movable[2–4].When nodes are scattered in an unfavorable environment,then these nodes are always under threat from many malicious attacks.For example,an attacker can examine the traffic pattern and theft of essential information from a network.There are different kinds of threats present in WSN.Some important threats are:

·Disclosure threat:It is a threat that involves the leakage of data or information from the system to any adversary node and poses a threat against the privacy of the information.

·Integrity threat:This type of threat involves that any unauthorized activity changes or modify the information.

·Denial of service threat:It is a threat that blocked the system for access by any malicious attacker.

Security is an important issue for the successful communication among sensor nodes.Security requirements are data confidentiality,authenticity,integrity,availability,reliability,flow control,key generation,and distribution methods.The security methods must fulfil these criteria such as scalability,robust,lightweight,and effective key pre-distribution[5,6].

Due to movement and some environmental factors,the nodes are not safe from external threats.In order to design Lucas polynomial based key management scheme,we studied and analyzed many schemes[7–11]and some of these schemes motivated us to design and propose a better solution which overcomes the problems in previous works.

The key generation and distribution approach play an important role in secure communication in WSN.In recent times,it is a very active research domain because of its challenging field.The previous researchers have proposed several techniques by using timestamps,identities,polynomial,random numbers,positions and various unique elements to produce the cryptographic keys for encryption and decryption[12–14].This paper includes a comparative analysis of recently proposed key generation and distribution schemes which fulfil the requirements of WSN applications.In the proposed work,the polynomial parameters are used in key generation and distribution and analyses effectiveness over other recent key management techniques to provide security during communication in WSN.

There are certain criteria by which key management schemes are evaluated to provide secrecy against various attacks.The key management technique must fulfil certain criteria for the efficient transfer of the message and secrecy of data.Some criteria are discussed below[15].

·Resistance:The key management schemes must provide the resistance against the malicious node which is deployed by adversaries.An adversary may attack and compromise some nodes in the network and replicate that compromised nodes.By this attack,the adversaries take control over the entire network.

·Revocation:If any node is compromised by the adversary,then it must be re-established.The network establishes a key management scheme that provides an efficient way to recover the compromised nodes.

·Resilience:The key management schemes must be lightweight and efficient due to the resourceconstrained nature of WSN.If any sensor node is captured by an adversary,then the key management methods must guarantee that the secret data of the whole network remain secured.The key management schemes must ensure that if a node that wants to either leave or join the network,the communication of the network is not affected.

In this paper,we propose a key management scheme that applies to WSN communication which has constraints like storage,power and computation.The proposed key management scheme can be used in hierarchical WSN.The main contributions of the paper are as follows:

·Study of existing polynomial based key management schemes

·Design of a novel(p,q)-Lucas polynomial based key management scheme to generate and distribute keys for sharing among base station,cluster heads and cluster members.

·Theoretical analysis for evaluation of the proposed work.

The other parts of the paper are organised as follows.Section II presents the background.Section III includes related work and summarizes the various recent works in the related domain.Section IV gives preliminaries which includes system model,adversary model,and design requirements.Section V presents the proposed approach with key generation using(p,q)-Lucas polynomial.In Section VI,detailed results are presented,and some observations are discussed.Finally,section VII concludes by giving some future research directions.

II.BACKGROUND

When any two nodes want to communicate through an unsecured channel or medium,then the sender node encodes messages by secret keys mutual by nodes,therefore,unauthorized nodes cannot read the encrypted messages without the secret key.

2.1 Key Management in WSN

To be responsible for secure communication,the messages are encrypted by secure keys and provide authentication for the sender node[16,17].The single key-based key management schemes are very efficient and less complex,but adversary can easily detect the key compromise in the whole network.Therefore,sensor networks use more than one keys based scheme to secure the network.Several key distribution techniques are used in WSN.Key pre-distribution distributes the key before the placement of nodes in the working field.So,nodes may communicate by using these secret keys[18].The keys are pre-distributed and works in three phases:key generation and initialization,key discovery and establishing of path key[19].A secret path is created when nodes distribute common keys and communicate via these links.In the key pre-distribution method,the keys are choosing randomly from the key pool[20].There are three ways to distribute the key before the deployment of sensors[21].

·Probabilistic:Keys are chosen randomly and arrive at the sensors.

·Deterministic:Keys are chosen by a definite pattern.

·Hybrid:It combines both probabilistic and deterministic.

Key pre-distribution distributes the key before the placement of sensor nodes in the network.So,the nodes make their network for communication by using these secret keys.These steps followed by the node which can make the channel secure for communication with the other node.A secure link is created when nodes can share common keys,and communicate via these links.The requirements of key management are a subset of security requirements of overall WSN.The operational requirement is treated as a constraint of key management schemes[22].

·Confidentiality:If any unauthenticated node wants to access data,then it is not revealed to other unintended nodes.

·Integrity:The channel and transmission medium must be secure;therefore,the data did not change during the transmission.

·Key freshness:When any node is compromised,then the set of keys between nodes must be refreshed and the old key is not used as a new one.

·Authentication:Data must come from known and verified sources;therefore,the origin of data must be secure and genuine.

·Robustness:When any node or communication link is compromised,then the WSN should be unaffected.

·Self-organization:The sensors are selforganized and flexible to form the best possible deployed structure and fault tolerance.

Surprise kept them silent while for one delicious moment they gazed into each other s eyes, and just then who should come up but King Gridelin, for it was into his kingdom they had accidentally strayed

·Scalability:The key management schemes must support from less to many numbers of nodes in WSN.

2.2 Types of Key Distribution Schemes

There are three types of key management schemes in WSN.These schemes fulfil the security and operational requirements of security.The different applications of WSN needs different key management schemes according to their requirements.There are three commonly used keys model.These keys model is maintaining relationships between the WSN security and operational requirements.The various keying models are network,pairwise,and group keying scheme.

First,the network keying management approach is an initial approach that has several advantages over the other two schemes.This approach has simplicity,easy management,and consumes less energy.This approach permits easy collaboration among sensors with their neighbor nodes.It can read and interpret each other’s data and satisfy the self-organization and availability requirements.This approach also supports scalability,reliability and flexibility since one key use for encryption for the whole network,and it does not alter when the size of the network changes.However,an unacceptable weakness with this approach is robustness.Consider any node of the network is compro-mised,and the network key is uncovered.With this network key,any adversaries can do eavesdropping on all data communicated in the network and also insert bogus data into the network,possibly distracting the communication of all networks.

The second key management scheme called a pairwise keying scheme where N–1 keys are stored at every node,where N is the number of nodes in a network.This approach has provided more security than a network keying scheme.It is more complex than the previous approach.The disadvantage of this approach is that it uses much more valuable power than network keying scheme.Similarly,key regeneration also suffers from some problems like scalability.Additionally,the accessibility needs are at risk as nodes are not monitored passively.Lastly,some pairwise key management approach has self-organization feature because they handle the scalability problem by dropping some pairwise keys,but it also creates some problem during key revocation and refreshing[23].

The previous schemes have some advantages and some disadvantages.The group keying scheme is the hybrid of network keying and pairwise keying scheme.It combines the advantages of previous both schemes.Consider a hierarchical network where the whole network is divided into several clusters.When any node wants to communicate inside the cluster,then it uses the same key or network keying approach.And when the network wants intergroup communication,then it uses a pairwise key management scheme.Therefore,for cluster members,the accessible constraint is removed by data aggregation without any cost while some degree of robustness is maintained.When any node is compromised,then only that cluster will be in danger where the nodes belong to.After that,the whole network will be safe.The main disadvantage of this approach is that the setup of the network is difficult.The formation of clusters-based network depends upon the application scenario.Network updation where any node wants to join or leave the network is also a challenge,it is necessary to update the defense elements by using cryptographic keys,otherwise,it makes a harmful effect on the existing network.So,hybrid key distribution techniques are used in WSN.

2.3 Architecture of WSN

Generally,the nodes in WSNs are deployed randomly and it has infrastructure-less architecture.To achieve the security and efficiency in WSNs,the sensors must collaborate among themselves. This architecture motivates to other protocol which provides energy-efficient routing,data aggregation and removing redundancy.There are mainly two architectures for sensor networks:

2.3.1 Flat Network Architecture

In this architecture,sensor nodes are randomly deployed where each node directly communicates with the base station.Each sensor is responsible to communicate and maintain security individually.This type of architecture is suitable where the collective information is not preferred.Figure 1 a)depicts the flat architecture of WSN.In this architecture,all the nodes play the same role and responsibility in the network.Due to the large number of nodes,it is not possible to assign special responsibility to any specific node.This architecture motivates to other protocol which provides energy-efficient routing,data aggregation and removing redundancy.

2.3.2 Hierarchical Network Architecture

In hierarchical network architecture,all the sensor nodes make a group called cluster.In each cluster,every node has some specific task with different roles and also have unique ID[24].In every cluster,there is a special node called Cluster Head(CH).Figure.1 b)shows the hierarchical architecture of WSN.The CH has chosen on different parameters like energy,degree,residual energy of a node etc.In each cluster,all the sensor nodes,collects the data and send it to the CH.The CH removes the redundant data and sends it to the Base Station(BS).The hierarchical network structure is more energy efficient due to the responsibility of CH among other sensor nodes.

III.RELATED WORK

Last few years,different researchers have proposed several key generation and distribution approaches[25–27]for sensor networks.These approaches have used both symmetric and asymmetric key management schemes based on various parameters such as computation complexity and power consumption.Many techniques have been proposed for the establishment of key distribution and secure key management.Figure 2 depicts a taxonomy of various key management schemes.In the following,we highlight the key generation and distribution approaches into families and designates the most relative content.

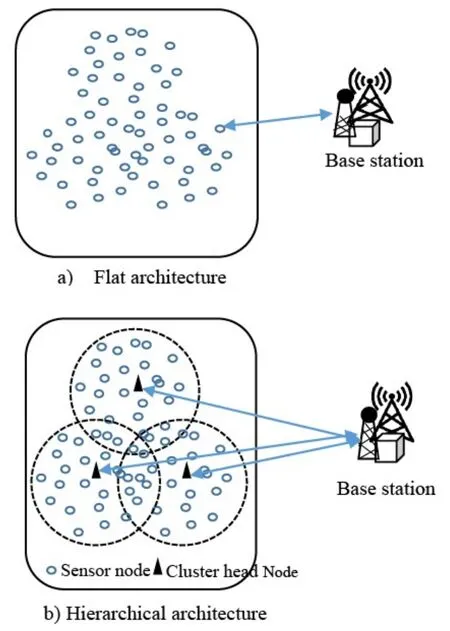
Figure 1.Architecture of WSN.

3.1 Random Key Distribution Based Schemes

Eschenauer et al.[19]proposed an initial key management scheme for WSN.This key management scheme comprises three phases,first is key pre-distribution,sharing keys and path-key formation.It considers that a node has a fixed set of keys called key ring which is selected arbitrarily without replacement from a set of enormous number of keys called key pool.In the key ring,each key has linked with ID of sensor nodes.This information must be stored in a controller node.This controller node is trusted by the network.Chan et al.[18]proposed a Q-Composite key management scheme that gives random key pre-distribution and multipath key reinforcement.It is also called a random pairwise key distribution approach.Q-Composite has a different kind of trade-off.The Q-Composite scheme is a powerful solution for security under little threat and it also detects high-level attacks.Du et al.[28]proposed a matrix-based random key management scheme.Matrix-based scheme maintains a matrix where c number of keys randomly selected from a large set of keys called key ring.A pairwise keys are selected which are common in key ring.This scheme provides authentication and also consume less energy.It supports robustness in the network.

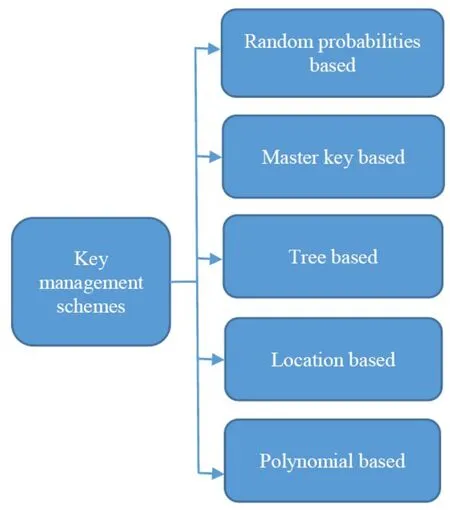
Figure 2.A Taxonomy of key management schemes.

Group-based trust management scheme(GTMS)is proposed by Shaikh et al.[29]and it is designed to defend against a black hole attack.To compute trust,GTMS is adopted to collect recommendations from all the nodes and calculate trust value.The trust is a combination of direct and indirect monitoring.Every cluster head has the collection of recommendations inside their cluster.The random key distribution schemes are simple,energy-efficient and easy for implementation,but it suffers due to its high complexity,high storage overheads and low accessibility.

3.2 Master Key-based Key Management Schemes

Another key management scheme that enhanced the security of keys is based on the master key of the diffie-Hellman algorithm.Gandino et al.[30]pro-posed a master key-based key generation and distribution scheme to manage symmetric keys.With the help of master keys and global puzzle or secret to initialize and produce pairwise keys.By these keys,secure communication environment for WSN is formed.Zhu.et al.[?]have given a key management scheme called LEAP+.The LEAP+scheme is to produce keys by using the transitory key.The transitory key is the combination of the master key and ID of the nodes.This key helps to adopt different types of keys according to the messages.Mainly,the pairwise key generation is the core of this scheme.

These above schemes provide more security against clone attacks and reduces initial key setup time.The main threat is that when the master key is compromised then the security of the network is at a high risk.

3.3 Location-based Key Management Schemes

Younies and Eltowieissy[31]proposed a Location-Aware combinatorial key generation and distribution scheme.This method uses a location and Exclusion Based System(EBS)for key generation.Based on location,the generated keys are pairwise,randomized and unique.It is also called SHELL because SHELL stands for scalability,hierarchy,efficiency,location and lightweight.This scheme offers regeneration of keys and improves the network safety against several threats such as node hijack and node compromise.The key management responsibility is distributed among all the nodes so,the computation complexity and storage overhead are reduced.The overload of the central node or base station is also avoided.In this scheme,the location is the key element to compute pairwise key between nodes.The SHELL provides defense against the collusion attack.These key management schemes support the change of network size which means node addition or deletion and also refresh the key by factoring the geographic location of nodes.

To be responsible for secure communication,the messages are encrypted by secure keys and provide authentication for the sender node.The single keybased key management schemes are very efficient and less complex,but adversary can easily detect the key compromise in the whole network.

3.4 Tree-based Key Management

Qin et al.[40]proposed an Elliptic Curve Cryptography(ECC)and AVL tree-based key management approach to secure the sensor network.The AVL tree is used to the public key of each node and their ID of a neighbor node.This key management approach is efficient in terms of energy,computation time,storage cost and communication cost.This approach also uses Elliptic Curve Paillieer Encryption(ECPE)cryptographic technique to defense against various security threats.This approach included another feature where keys are updated frequently.Yao et al.[41]have given a key distribution approach called LKH++for a cluster based sensor network.In LKH++,keys are maintained and saved in a tree data structure.These keys are used for cluster or group.The tree can be maintained by the sink node.This scheme regenerates and rekeying the keys when it required for network.LKH++improves network security and robustness against node capture attack in sensor network.Swaminathan et al.[42]proposed a scheme where the structure of the wireless network in developing with a combination of Distributed Spanning Tree Structure(DSTs)and effective low-cost key generation method.The Low cost Key Management Model(ELWKM)is more effective in terms of energy cost,time and storage.Ren et al.gave an effective public key cryptography-based scheme which is an aggregation of several encryption/decryption methods,Bloom filter and the Merkle hash tree[43].The elliptic curve discrete logarithm problem uses to establish a key management scheme by using key threshold theory.

The tree-based key management schemes give better performance on storage,computation,and communication overhead.It also provides perfect scalability where the network gives the same performance during node addition and removal.

3.5 Polynomials Based Key Management Schemes

There are several polynomial based key distribution approaches proposed by research fraternity in recent years which are depicted in Table 1.Shamir[44]introduced the first polynomial based scheme in their paper to implement threshold secret sharing.To certify safe inter-group communication,Lu et al.[32]proposed a unified framework using classes of nodes and the de-gree of a polynomial for a distributed key management approach in heterogeneous WSN.In this framework,they generated random bivariate polynomials pool to establish a key between sensor nodes.This framework also considered various parameters of heterogeneity in the network.Fan et al.[45]proposed a key management method based on lightweight polynomial for distributed WSN.This protocol mitigated common security attacks and also provided secure communications via one to one and many to one using polynomial based keys(pairwise key,cluster key,and group key)and also provided authentication using a probabilistic local broadcast authentication protocol among neighboring nodes.Wang et al.[33]proposed a polynomial inspired key management scheme to offer the security of personal key shares.It uses p-degree polynomial F(x)for secure inter and intra class communication.Consider a a network having two groups of sensors,the first group called as G1 and the second group called as G2.If P(v)is a key used by a member of group G1 to encrypt the multicast message to members of group G2.To decrypt this message using key P(x)by members of group G2 received by members of group G1,the group controller assigns a polynomial to each member of G1 and G2.In this key distribution scheme,a revocation polynomial and a particularone-way hash function is used to defend against the collusion attack.The broadcast communication is updated by revocation polynomial which is generated by a one-way hash chain utilization method.This scheme shortened the communication overhead and removes the collusion attack.

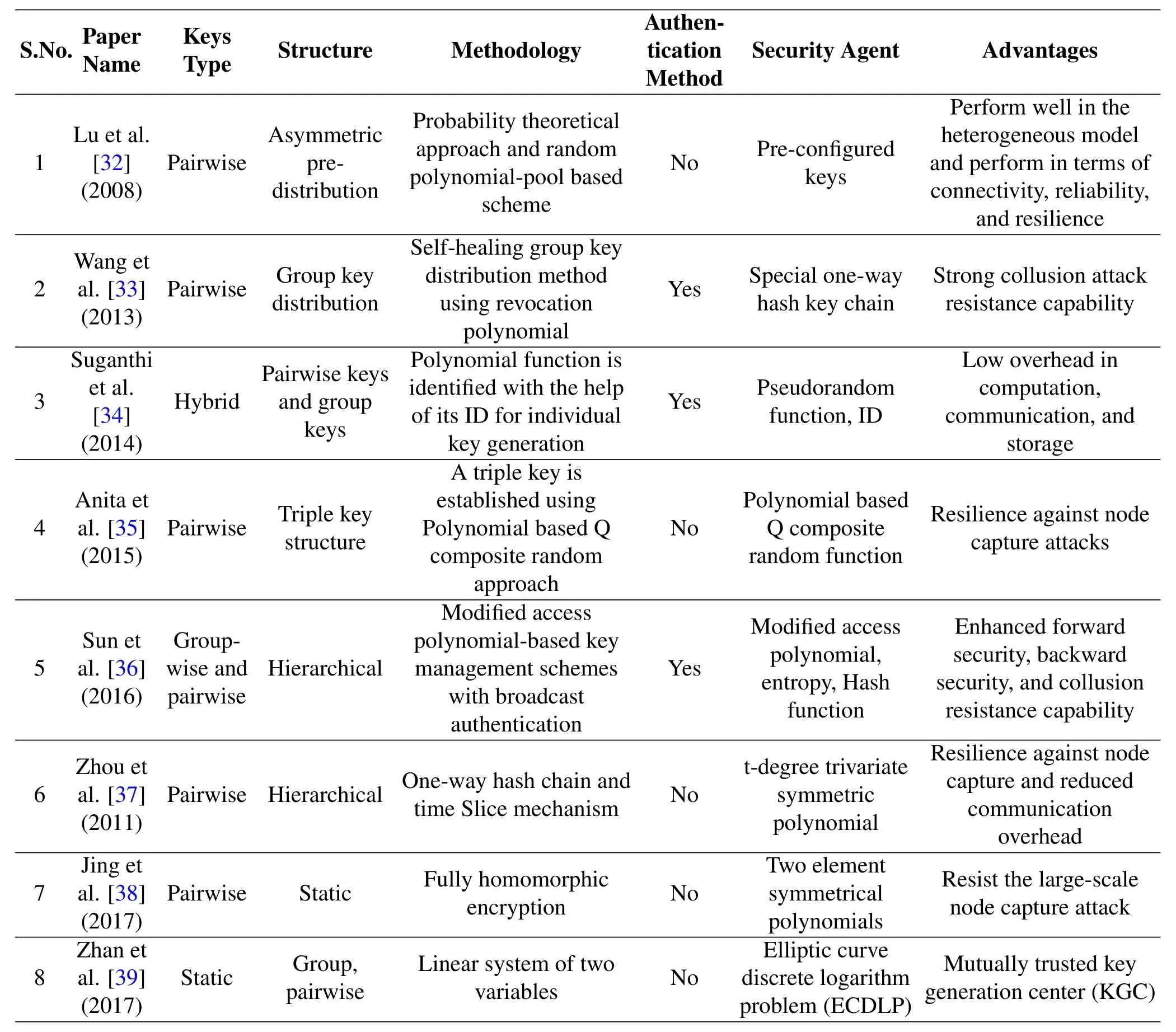
Table 1.Summary of polynomial based key management schemes.

Suganthi et al.[34]calculated the keys(individual keys and the pair-wise keys)during initialization using polynomial functions.In their approach,the base station shared the individual key and the neighbour nodes shared the pairwise keys.The other nodes shared the group keys.So,by this method,the communication overhead is reduced.Anita et al.[35]had given Q-composite random scheme based on polynomial,which generate a triple key for communicating among the sensor nodes.This is the polynomial poolbased method to establish secure communication between them.Sun et al.[36]proposed a key management scheme based on polynomials by self-heal keys.The improved polynomials and broadcast authentication scheme can provide secure communication and collusion resistance.It is using a group of slidingwindow and improved polynomials to produce pairwise keys among the controller node and other sensor nodes.The two unique approaches Sch-I and Sch-II were also proposed.The Sch-I method proposes the idea that pairwise keys are established and shared between the controller node and other sensors.Sch-I can be updated dynamically according to the network.Sch-I declines the vulnerability as other nodes do not have any information about this polynomial.The forward security is provided by a one-way hash function while backward security by using modified polynomial.Sch-II removes hash chain and strengthen the security.In this method,they improved the collusion resistance and avoided the flaws of acceding polynomials.Zhou et al.[37]proposed a unique,effective and dynamic key management approach for sensor networks.There is a combination of ECC,p-degree and trivariate symmetric polynomial that were combined to generate efficient keys.Time slice mechanism is used to update the key dynamically.One-way hash chain technique was designed to lower the cost for communication in key generation and update process.

Ramkumar et al.[46]have given a novel approach in key management using Chebyshev polynomials to generate key for ad hoc networks.They used properties of Chebyshev polynomials to secure communications.Jing et al.[38]have proposed symmetric polynomial which is based on a calculation-based algorithm.By using homomorphism encrypted mechanism,it generated pairwise keys.By this approach,the network is protected from node capture attack.Due to properties of an asymmetric polynomial,this pairwise keys are unique,random and strong which fulfills the requirements of a good key management scheme.Zhan et al.[39]proposed a system of equation-based key management scheme to produce pairwise keys among sensor nodes.By these pairwise keys,the sensor network communicated and transmitted messages secretly.The system of equations has properties that all the equations have only one solution.So,the established keys are lightweight,efficient and secure.The cutting point of linear equations used to generate secret shared keys.These pairwise keys are used to protect the network from various attacks in sensor networks.The keys are generated by the equations called the associated key.Due to the complexity of polynomial equations,this method uses linear equations that have only two variables and Exclusion Basis System(EBS)to generate keys and implement the key management in that network.The advantage of this approach is that it provides a good key establishment in comparison to other ordinary key schemes and also other performance metrics are unaffected.

Dinker et al.[47]proposed a multivariate symmetric polynomial and matrix-based key management scheme.This scheme uses polynomial and matrix to generate keys between the sink node and the cluster head.The protocol can make a secure network for future communications.It can maintain the matrices at the sink node,multicast control node,and cluster head node.When any node is updated,then due to multivariate symmetrical polynomial,matrices are also updated.In this method,the key management and authentication effectively work with sensor nodes and also give efficient results when nodes are updated frequently.

IV.PRELIMINARIES

To enhance the security and key connectivity,a Lucas polynomial based key generation scheme is proposed.The proposed method is applied in a hierarchical sensor network to generate the keys using Lucas polyno-mial and to provide authentication and to secure the network.In the following,we briefly introduce the network model considered,(p,q)-Lucas polynomial and its properties.

4.1 Network Model

We assume that WSNs have clusters of sensors and a single base station that behaves as a sink for the data collection.We consider WSN as a homogeneous network where each resource has the same primary energy,bandwidth,link capacity,and communication distance.Data collected by each sensor is transmitted over multi-hop paths to the sink node to save energy consumption and also to increase the lifetime of the network.A hierarchical sensor network has the following elements:

·Base Station(BS):The proposed scheme assumes that the base station is secure,less failure,memory,power,bandwidth,processing capacity,communication overhead and other resource constraints.

·Cluster Heads(CH):In hierarchical routing protocol,all the sensor nodes make a group called cluster.In each cluster,every node has some specific task with different roles and unique id.In every cluster,there is a special node called Cluster Head(CH).The CH has chosen on different parameters of a node such as its degree,residual energy etc.Each sensor node collects the data and sends it to the CH.The CH removes the redundant data and send it to the Base station.

·Cluster Members(CM):Any cluster has two types of nodes.One is CH and the other is Cluster Member(CM).Each cluster member of a cluster senses data from the environment and transmit it to the CH.After that,CH aggregates all the data from the CM nodes and send it to the base station.

4.2 (p,q)-Lucas Polynomials

The Lucas polynomial is defined recursively and belongs to a family of polynomials called Fibonacci polynomial.The Lucas polynomial was first introduced by Bicknell in 1970.

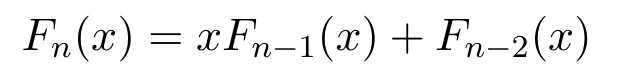
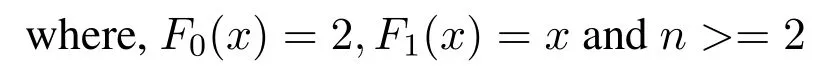
The(p,q)-Lucas polynomial is summarized as follows[48]:

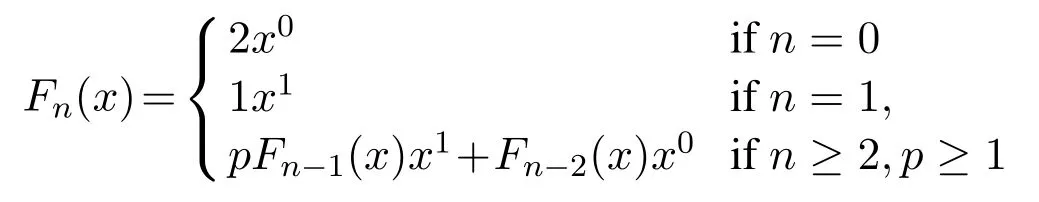
Here,p represents the random base number and q is the value of x calculated by the sensor nodes.Lucas polynomials also obeys the recursive definition.The first 10 polynomials are as follows when the value of p=1[49].

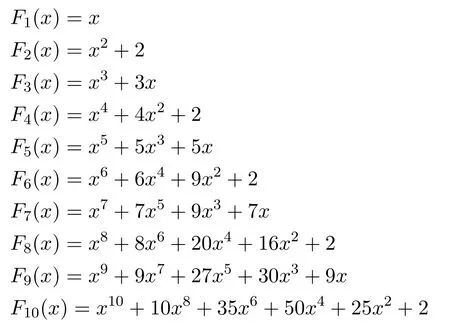
These Lucas polynomials satisfy the following additional properties with the help of Fibonacci polynomials(fn(x)):

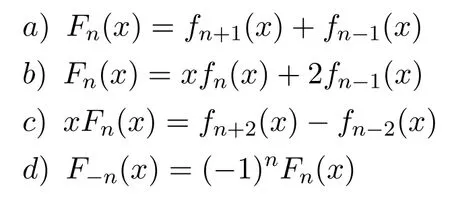
where Fibonacci polynomials fn(x)can be defined by Fibonacci-like recurrence relations,and yield Fibonacci numbers.

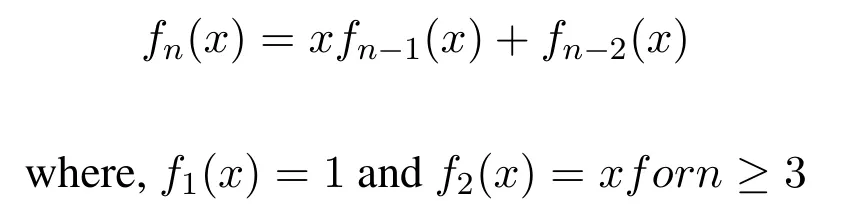
If we arrange the coefficients of different order of Lucas polynomials in ascending order,then the sum of elements along the nthrising diagonal is 3·2(n-1)/2where,n is even and n＞=2.

4.3 Properties of(p,q)-Lucas Polynomials

The Lucas polynomial is the polynomial based on Fibonacci series.The Lucas polynomials must obey the following properties[50].

(i)(p,q)-Lucas polynomial can generate any degree of polynomials

We can generate any degree of polynomials with the help of Lucas polynomial.Table 1 and Table 2 represent Lucas polynomials for different values of p and q.When the value of p=2,then the generated Lucas Polynomials are as follows:

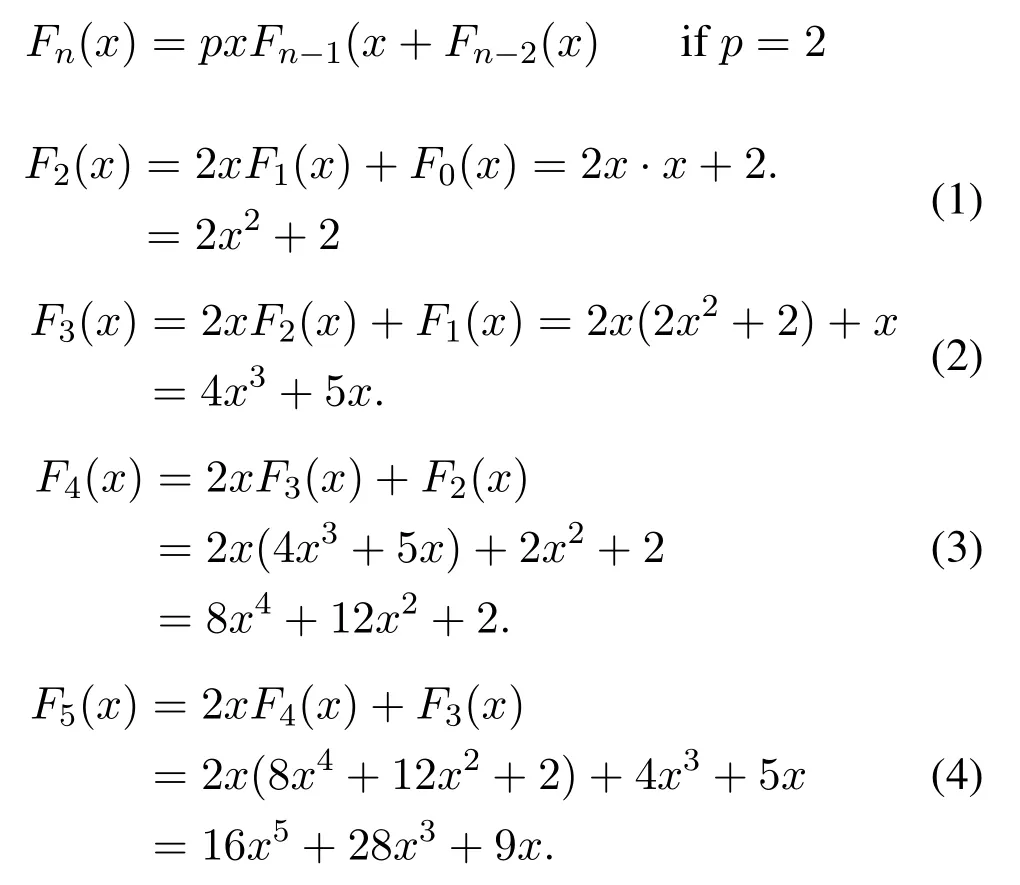
Similarly,when the value of p=3,then the generated Lucas Polynomial are as follows:

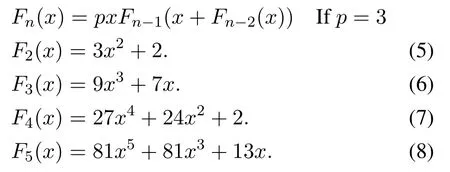
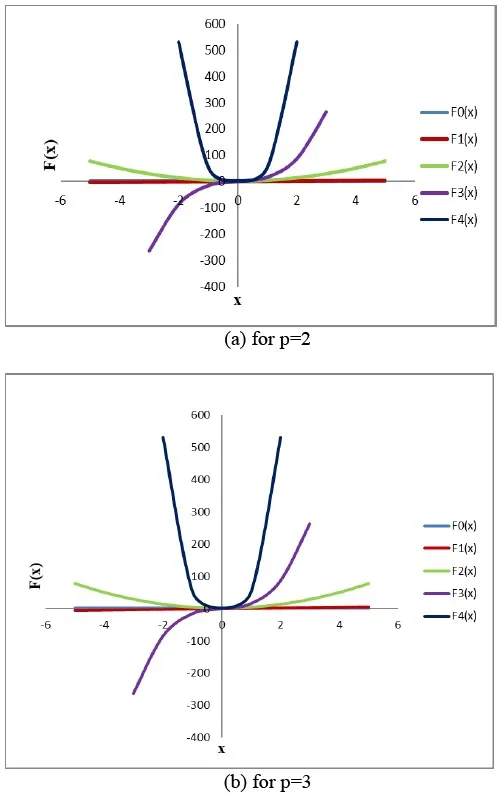
Figure 3.Dimensional geometries corresponding to Lucas polynomials.

The polynomials having the data of keys can be plotted using the curve fitting method[51].Figure3(a)and Figure 3(b)represent the graph of dimensional geometries that correspond to the Lucas polynomials with a different value of p.

(ii)(p,q)-Lucas polynomials are recursive

We can represent the Lucas polynomial as a recursive polynomial[49].

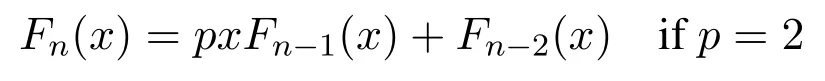
From Equation(1)

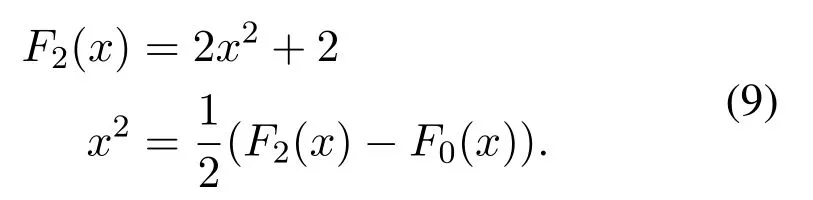
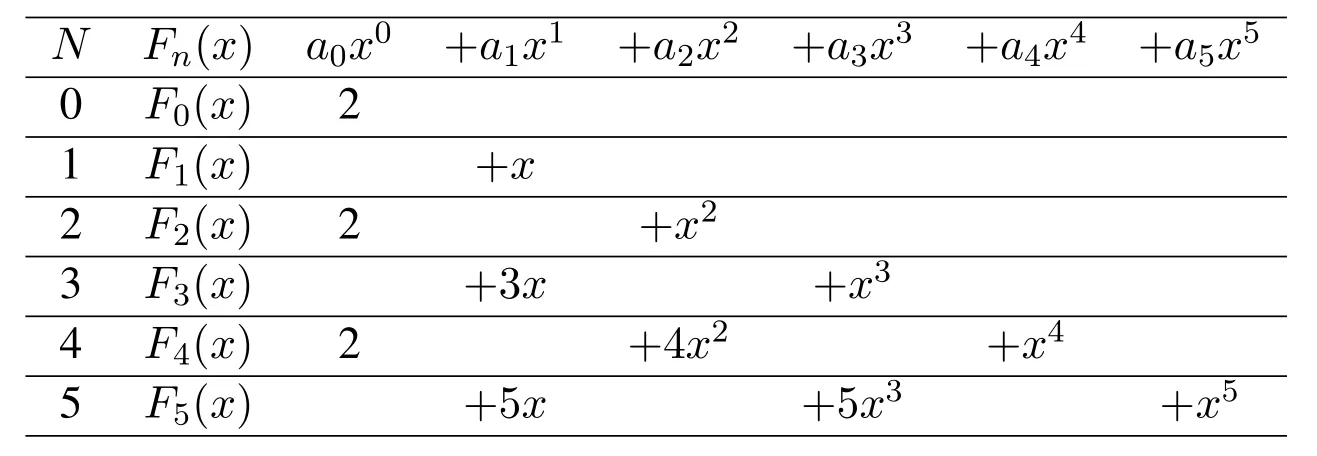
Table 2.Lucas polynomial.

Table 3.Lucas polynomials for the different value of p and q.

From Equation(2)

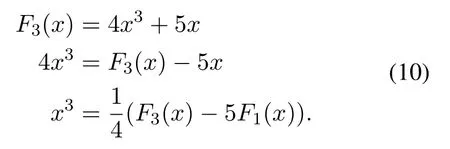
From Equation(3)

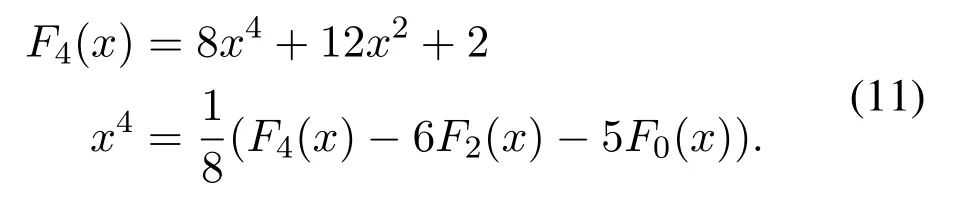
From Equation(4)

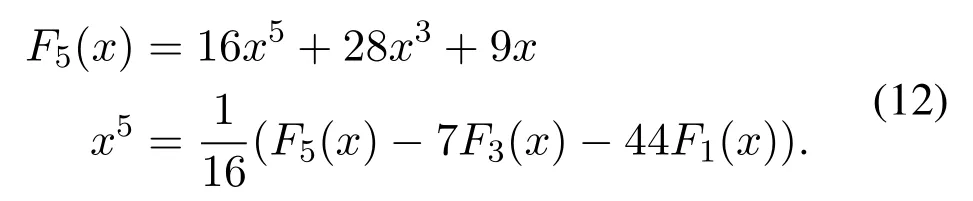
One property of Lucas polynomial is that any equation can be converted into Lucas polynomial form.Consider any random equation f(x)=4x2+5x+8 that we have to convert into Lucas polynomial form.Put the value of x2from Equation(5)in this random equation.Then we obtain the following:

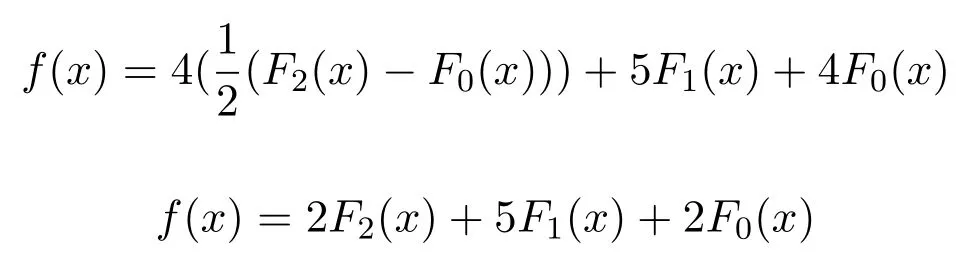
V.PROPOSED APPROACH

In this Section,we present key generation mechanism using(p,q)-Lucas polynomial.Initially,every sensor node has a set of symmetric keys.With these symmetric keys,all the sensor nodes of the given WSN network transmit their IDs and data securely.This proposed approach is used to generate secure pairwise keys for secure communication in hierarchical sensor networks.The major issue in key generation and management with the polynomial is that the value of multiplicative is high.When the number of nodes increases in a cluster,the computation and communication cost of cluster head also increases and thereby residual energy decreases.Also,the storage cost and multiplicative of polynomial are increased for restoring their IDs.The proposed key management scheme is used in hierarchical WSNs.Formulation of cluster and choosing a cluster head is the first task.After that,cluster head selects a random polynomial Rx and ran-dom base number p,to convert it into Lucas Form.

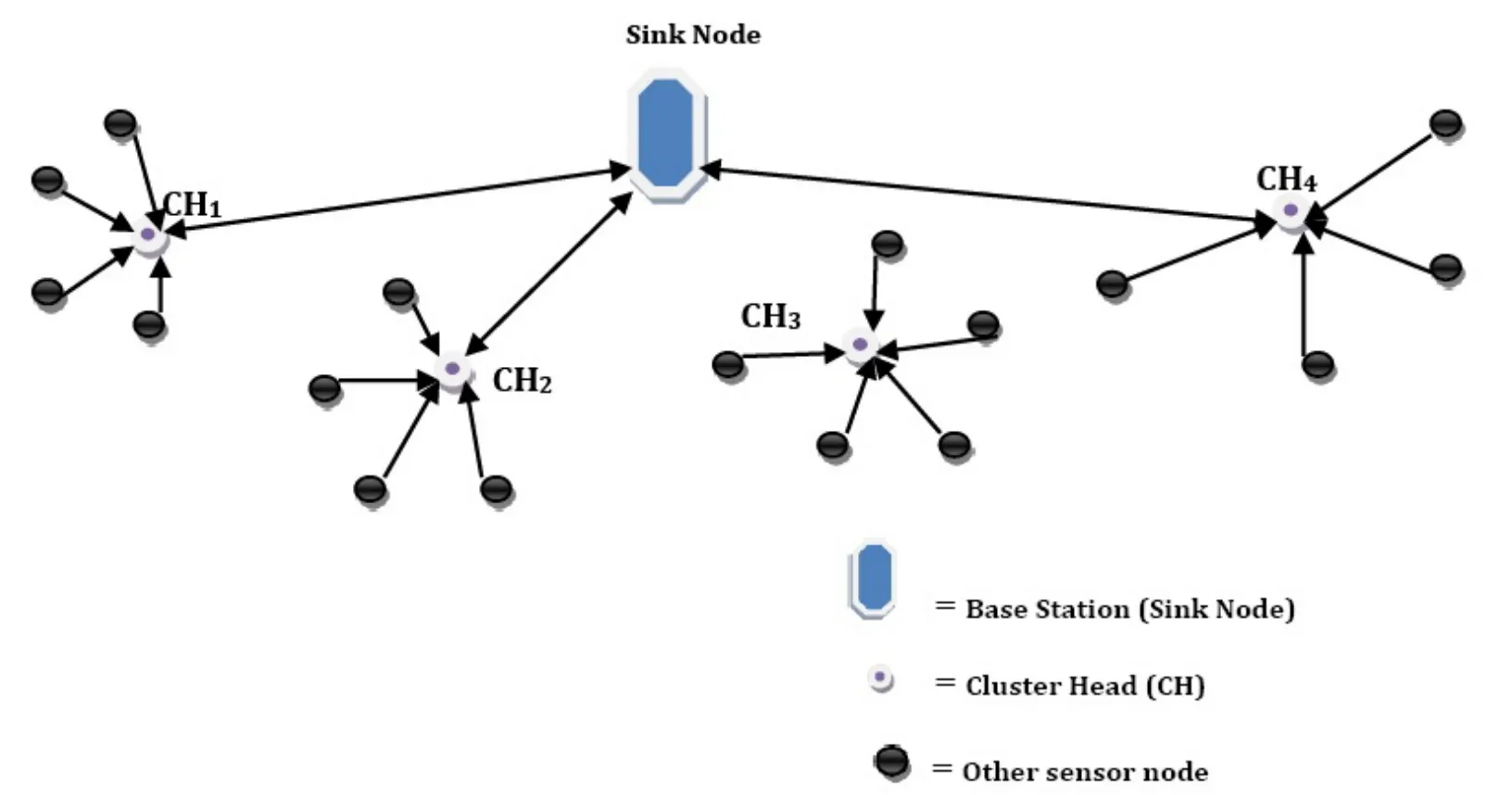
Figure 4.Hierarchical sensor network.

The proposed method randomly chooses a cluster head who takes the responsibility to generate Lucas polynomial.Suppose one of the cluster heads select random equation Rx=16xa+28xb+104 and uses preloaded value of p=11.Using this base number and equation,the cluster head generates a Lucas function of that random equation Fa(x).This Fa(x)is shared with other cluster heads,base station and other sensor nodes inside the cluster.

Consider the nodes on the same level that calculate the value of Fa(x)on a particular x.If nodes are on different levels(cluster head and non-cluster head node,cluster head and sink node)then,it calculates Fa-1(x)or Fa+1(x)on a particular x.Each sensor node preloads the base number.One of the cluster head members chooses a random equation and value of x.The CHs convert this equation in Lucas polynomial form and share it to the base station,other cluster head and sensor nodes.If other cluster head members want to communicate with each other then they calculate the value of that Lucas polynomial.This value is the key and used for communication between cluster heads.When cluster heads want to communicate with the base station,then,they generate a higher degree of that polynomial and calculate value on them.This value is working as a key for communication between the base station and cluster heads.

When the other sensor nodes want to communicate among themselves,then they generate one lower degree Lucas polynomial and calculate the value of that polynomial equation.This value works as a key and used for communication among sensor nodes.Consider the hierarchical structure of a WSN shown in Figure 4.In this,one sink node(SN)and four clusters of sensors are present.Each cluster has a Cluster Head(CH)named as CH1,CH2,Ch3,CH4and other are sensor nodes.The proposed method selects CH1 as administrator node among the CH1,CH2,Ch3and CH4.The CH1generates the random equation f(x)=8x5+5x4+9x2-8x+9 and value of x=4.Then,convert this random equation in Lucas form by replacing the value of x5,x4,x2from the Equation 8,Equation 7 and Equation 5.For the following random equation,f(x)=8x5+5x4+9x2-8x+9 the Lucas equation is as follows when the base value p=2.

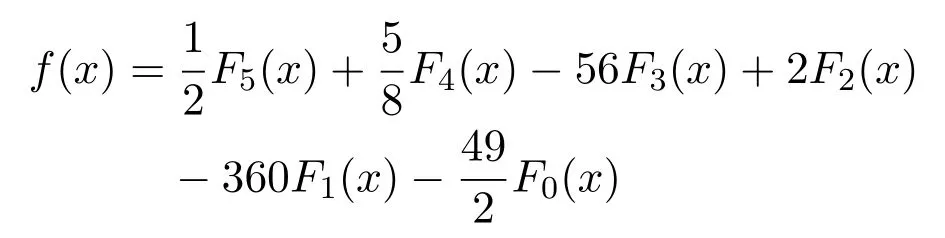
This equation is shared by CH1to all other nodes including the Sink node,other cluster heads(CH2,Ch3and CH4)and non-cluster nodes of the network.As the base number and initial equation are already fed to different sensor nodes,nodes are authenticated when they join the network.If any adversary tries to join this network,then getting the base value and random polynomial is a difficult task.Therefore,only authen-ticated nodes can access encrypted messages.During updating of network,such as new node joining or existing node leaving, it must preserve forward and backward secrecy.The(p,q)Lucas polynomials and random equation must be replaced to secure inter-group communication.Consider the following three cases:Now,we demonstrate computation of key for the following three different cases:

Case 1.If any of CH2,CH3,or CH4wants to establish communication with CH1then,they calculate F5(x)which is given as follows:

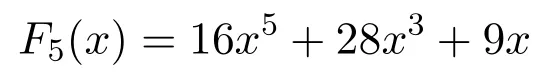
Put the value of x in F5(x).Suppose the value of x=1.Then,the value of F5(x)=53 is a key that is calculated by CH1,CH2,Ch3and CH4.

Case 2.If other sensor nodes want to communicate with CH1,then,they calculate F4(x)which is given as follows:

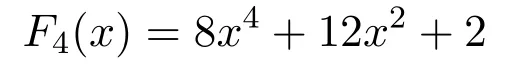
Put the value of x=1 in F4(x).The value of F4(x)=22 is a key that is calculated by both CH1and other sensor nodes.

Case 3.If Sink node wants to communicate with CH1,then it calculates F6(x)which is given as follows:

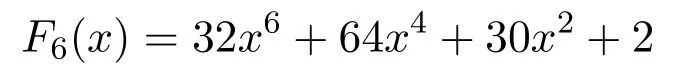
Put the value of x=1 in F6(x).The value of F6(x)=128 is a key that is calculated by both CH1and other sensor nodes.In every session,the nodes follow the same procedure.

VI.RESULT AND ANALYSIS

The polynomial based approach has many advantages over simple random number generator,master key based and matrix based in terms of scalability,key connectivity,resilience,storage complexity,processing complexity and communication complexity.In general,attacks affecting WSN are usually eavesdropping,active and passive adversaries.Passive adversary obtains some data by analyzing traffic without any physical access,and active adversaries obtains data and information by capturing packet or node.The proposed scheme is secure against passive attack and active attack,and we will explain the reason below.

·The key generation schemes using simple random number generator have many instances where implementation of this resulted many vulnerabilities.There are some of the major threats that should be considered.These threats are weak keys,incorrect use of keys,re-use of keys,nonrotation of keys,inappropriate storage of keys,inadequate protection of keys,Insecure movement of keys, non-destruction of keys, lack of resilience and many insider threats.

·The Shamir’s secret key algorithm used to help sensor node to regenerate the polynomial function after getting necessary key part, this approach may compromise the security.After that this node can abuse the polynomial and it can create key shares of its own.This problem solved by our Lucas polynomial based key shares algorithm where the adversaries cannot have any clue about polynomial function and their important parts.

·In our proposed approach all the nodes must share the information of keys in the form of Lucas polynomial.So,if any adversaries can get this message but they are not able to find the value of(p,q).The value of(p,q)is decided by the base station and embedded to all the before deployment.

·The Lucas polynomials can provide secrecy,accuracy,and stability.Also there is no limit to the degree of the polynomials

·In this paper a random polynomial is converted in Lucas polynomial format and evaluating it.The Lucas polynomial are generic and can hold any base number for generating the successive polynomial sequence.The polynomial which is taken for key management is evaluated based on the Lucas number sequences.

·There is no need of any encryption of decryption operation during key sharing.Each key is generated at the node himself.Only random polynomial is shared in the form of Lucas polynomial.It is very difficult to find the keys on basis of information shared by the nodes.

This segment also represents and evaluated the performance of(p,q)Lucas polynomial based key man-agement scheme.The efficiency and safety analysis,computation complexity analysis storage overhead analysis,communication overhead analysis and superiority of Lucas polynomial over Lagrange’s polynomial[52]and curve- fitting have been discussed.The various notations used in the discussion is depicted in Table 4.

Table 4.Notations used.

6.1 efficiency and Safety Analysis

Below we analyze the efficiency,attack model,rekeying for a member leaving and safety of nodes of the proposed scheme.

a)efficiency:In some recent previously proposed schemes the cluster head or group controller encrypts the pairwise key and sends it to all members;however,in our key management scheme,the cluster head converts the random equation in(p,q)-Lucas polynomial form and then send it to all members.So,performing the encryption and decryption is more complex than converting in(p,q)-Lucas polynomial.

b)Attack model:There are mainly two types of attacks that an adversary node can perform,e.g.,active and passive attacks.In passive attack,an adversary analyzes the traffic by overhearing and get some information about the key without any physical access to the node.However,in active attack,an adversary obtains some information of key that leaked through the physical access of a node.The proposed scheme of key management provides a defense against node capture and analysis of traffic as it is hard to guess random polynomial and base numbers from Lucas polynomial.At every level,like a base station,cluster heads and cluster members,the order of Lucas polynomial is different which is hard to guess.

c)Re-keying for a member leaving:If any sensor node leaves the group,the re-keying must be performed to ensure forward secrecy.When any node is expelled from the group,then the new base number and Lucas polynomial are shared with the help of that sensor node ID.With the help of a new base number and Lucas polynomial,all the members of the group,generate a new key and communicate with this new key.

d)Safety of nodes:Lucas polynomials based key management scheme prevents adversaries to read the information from the nodes.The base value is preloaded into the sensor nodes and the random equation is converted into Lucas polynomial form.At every level,different degrees of Lucas polynomial are used.So,it is hard to guess the base number and equation to calculate the key value at any level.

6.2 Computation Complexity Analysis

In the proposed method,the communication keys are encrypted while sharing them to other nodes by a master key as used in previous key management techniques.However,in the proposed approach,a CH shares the Lucas form of random equation which is needed to encrypt the Lucas form of a random polynomial.It is hard to guess the random equation and base number q.So,for other nodes,calculating the polynomial and generating the key is more efficient than existing methods or approaches.

The computational complexity of the key generation in the proposed method is calculated by generating a polynomial function of odd or even degree polynomial function as given below.

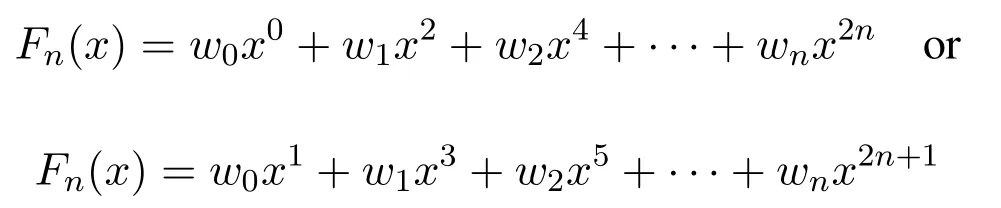
where,w0,w1,w2,···,wnare the constant multipliers.The computational complexity of Lucas polynomial is better than the normal polynomial function.

Consider the following normal polynomial function

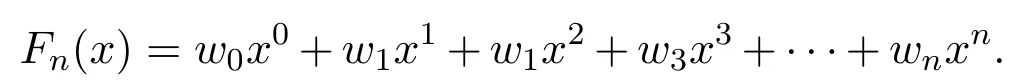
If we consider the addition and multiplication operation costs i.e.multiplycostand additioncostequal to c,then the computational complexity(CN)in case of normal polynomial shall be

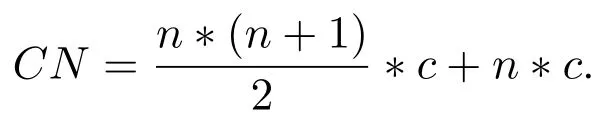
In our proposed approach,since a Lucas polynomial is generated using either even or odd degree of polynomial.So,in that case the complexity will be reduced which is presented below.

Consider our Lucas polynomial generated the following polynomial

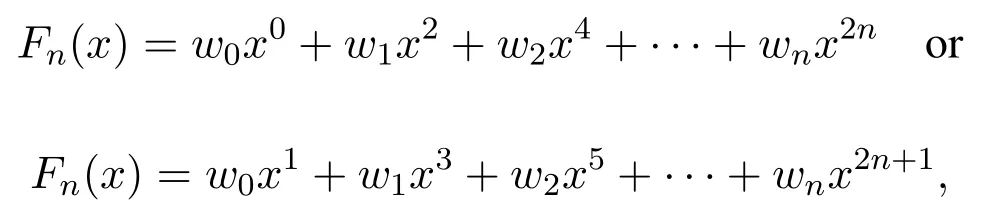
Then,the complexity of this Lucas polynomial shall be as follows.

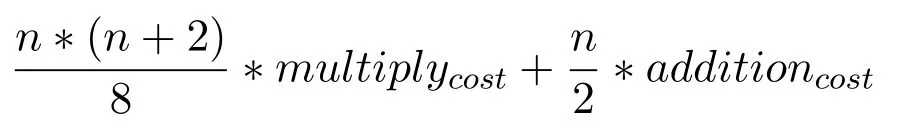
If addition and multiplication operation costs(i.e.multiplycostand additioncost)are considered equal to c,then,the computational complexity(CL)in case of Lucas polynomial shall be

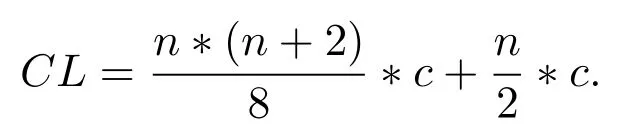
Figure 5 depicts the comparison of computational complexity of the key generation using regular generating polynomial and Lucas Polynomial functions.It can be observed that computational complexity in our case is lower than existing one.

6.3 Energy Consumption Analysis

Assume that there are NCH number of cluster heads and NCM number of cluster members.The random polynomial is RPand value of its parameters are p and q.During the initialization of the network,the value of RP,p and q are predefined.By using RP,the cluster head can generate three Lucas polynomials of order Fn(x),Fn+1(x),and Fn-1(x).After putting values of p and q,we get the pairwise keys to communicate with the base station,other cluster heads and cluster members.

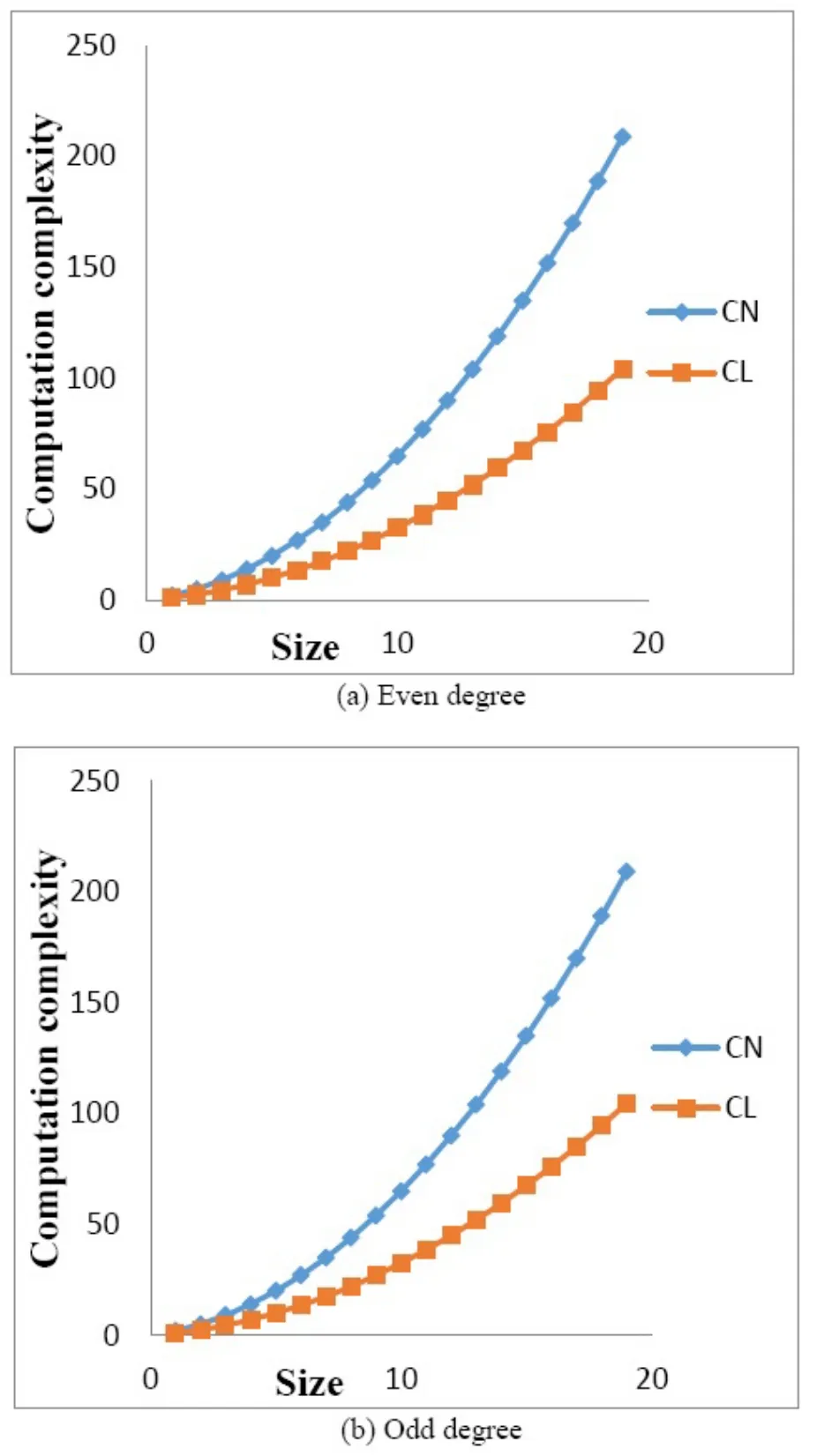
Figure 5.Comparison of the computation complexity of Lucas polynomial with general polynomial.

Therefore,each cluster head generates a minimum of three pairwise keys.The first key is used to communicate cluster head with the base station,the second key is used to communicate cluster head with other cluster head and the third key is used to establish communication among cluster heads to cluster members.

Similarly,each cluster member generates two pairwise keys,one to communicate with a cluster head and the other is used to communicate with other cluster members.As sensors are energy-constrained devices,it has very less battery power than any other communication devices.The total energy consumption during key establishment in the network is given as follows.

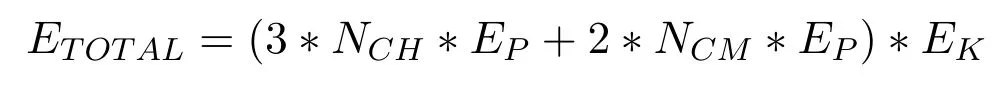
Number of iterations,addition and multiplication are the important attributes to be taken for evaluation.

6.4 Storage Overhead Analysis

As each sensor node needs to generate a pairwise key for communication,so it stores a random equation and value of(p,q)during initialization.Each cluster head needs to store three keys while each cluster member needs to store two keys.If we assume that a pairwise key takes k space and for random equation and parameters,it takes s spaces,then a cluster head takes a minimum of 3*k+s storage space while a cluster member takes 2*k+s storage space.

The total space consumed during one session shall be as follows.

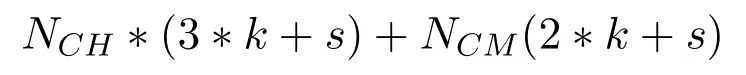
The PRK[47]scheme assumes that each sensor can store keys.Each key takes k space and s space for storing any polynomial.Therefore,each sensor node can take minimum storage space as given below.

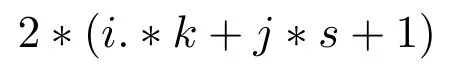
and overall network can take storage space as given below.

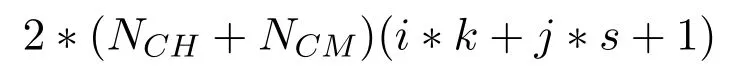
where i and j are the number of keys and equations respectively.

Table 5 depicts the performance comparison of the proposed method storage capacity and other existing approaches such as distributed key management schemes such as(DKMS)[53],three-factor authentication scheme(LKH)[54]and PRK[47].From the Table 5,it can be observed that storage overhead is less compared to existing ones.

Table 5.Number of keys stored by a single node in one session.

6.5 Superiority of Lucas Polynomial Over Lagrange’s Polynomial[54]and Curve- fitting

The security of WSN can be achieved with various security approaches.Key management is an efficient and secure method to provide defense against various security threats and it also provides authentication.In a numerical approach,Lagrange polynomials are used for polynomial projection for a set of different points(xk,yk).This polynomial is least degree polynomial where at each point of xk,it gives the corresponding value of ykand similar polynomial can be achieved by different methods.The basic function of Lagrange polynomial is a key share generation using(x,f(x)).Another key management method called curve fitting where data points are plotted on a graphical environment.Each curve is represented as a secret polynomial.The approximation technique is used to generate a polynomial equation which is not accurate.The major problems in Lagrange polynomials and curve fitting are accuracy,computation speed and power consumption.The higher-order polynomials consume more energy.These problems can be overcome by using Lucas polynomial based key management scheme.The Lucas polynomial is recursive,accurate,feasible,scalable and secure.It takes less addition and multiplication operations than Lagrange polynomial and curve fitting.The supremacy of Lucas polynomial over Lagrange polynomial and curve- fitting can be observed in Figure 6.

VII.CONCLUSION AND FUTURE DIRECTIONS

Wireless sensor networks are typically deployed in remote and unattended terrains to monitor,process and collect time-critical and sensitive data.For secure communication,sensor nodes rely on their secure credentials,authentication of nodes and defense against various security attacks.Key management techniques play a vital role for secure communication.The proposed scheme based on(p,q)-Lucas polynomial generates session symmetric key for payload delivery and this stealthy key is single time operational.Lucas polynomial can generate polynomials of different degree.By this approach,the hierarchical sensor network is highly secure,and storage overhead complexity is also less as the key pool uses a lesser number of keys.Moreover,time complexity is also lower as it takes half of the time rather than generating normal polynomial.The theoretical analysis show that the proposed model works efficiently for secure communication.The approach can also overcome the disadvantages of Lagrange’s polynomial and curve- fitting based key management scheme.

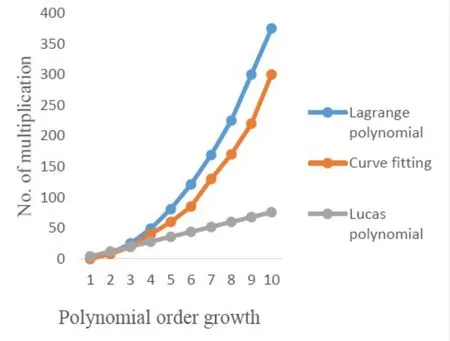
Figure 6.Supremacy of Lucas polynomial over Lagrange polynomial and curve fitting.

In the future,proposed Lucas polynomial-based authentication and key management scheme for a particular session can be extended efficiently for a multisession scenario in WSNs or Internet of Things(IoT)networks.