具有动态边界反馈的Timoshenko梁的能量衰减估计

严佳梦，鲁轶戈，章春国

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

近几十年来，随着柔性结构在机器人学和空间科学的广泛应用，带有柔性结构的控制问题引起众多数学工作者及力学工作者的极大关注，研究人员从各个层面广泛研究以柔性结构作为主要构件的系统模型，如Euler-Bernoulli梁模型、Rayleigh梁模型和Timoshenko梁模型，其中尤以Timoshenko梁模型能更精确地描述这一类柔性结构构件模型，得到许多实际应用[1-3]。不少研究者致力于具有动态边界的弹性梁系统稳定性的研究。文献[4]对具有动态边界Euler-Bernoulli梁的指数稳定性进行研究，得到了很好的结果；文献[5]研究了一部分边界是动态边界的Timoshenko梁系统的稳定性；文献[6]应用Hilbert唯一性方法得到了具有动态边界的均质Timoshenko梁系统的精确能控性；文献[7]应用线性半群算子理论得到了具有边界反馈的非均质Timoshenko梁的指数稳定性。受文献[4-6]处理问题方法的启发，本文研究一类具有动态边界非均质Timoshenko梁系统的能量一致指数衰减性质，采用的反馈方式与文献[7]所采用的反馈方式相类似。

1 问题的提出

具有动态边界Timoshenko梁系统如下：

(1)

本文中，反馈常数与文献[7]的反馈常数不同，因为文献[7]研究的不是动态边界反馈，无需系数强制条件，本文要求k2>0,k4>0，若不然，会造成边界条件不相容。

为了得到系统的能量衰减估计，需要如下自然假设：

ρ(·),Iρ(·),K(·),EI(·)∈C1[0,L],ρ(·),Iρ(·),K(·),EI(·)≥C>0,x∈[0,L]

(2)

式中，C为一个正常数。

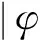
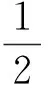
(3)

设

V=H1(0,L)×H1(0,L),H=L2(0,L)×L2(0,L)

这里，Hm(0,L)是m阶Sobolev空间[8]，且

并设

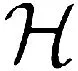
具有范数

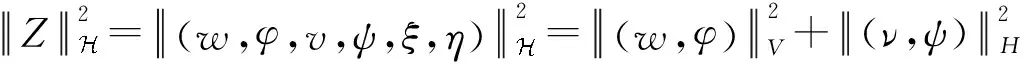
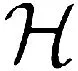
D(

(4)

和

(5)

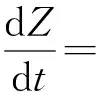
2 系统的解的存在唯一性和谱性质

定理1假设(2)成立，那么是上的压缩C0-半群et的无穷小生成元。

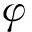
(6)

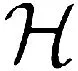
(7)

即解方程

(8)

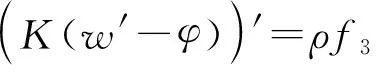
(9)

(10)

于是，式(10)结合式(8)的最后一式在x=L处可得：

(11)

再由式(10)在[x,L]上积分，可得：

(12)

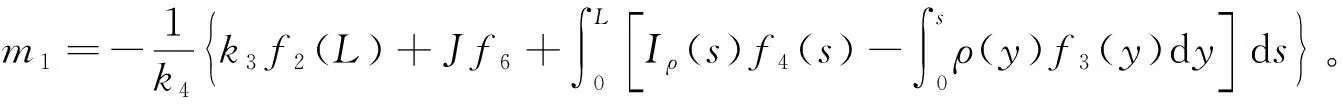
同理，式(9)结合式(8)的倒数第2式，在x=L处可得：

(13)

由式(9)和式(12)可得：

(14)

式(14)在[x,L]上积分，可得：

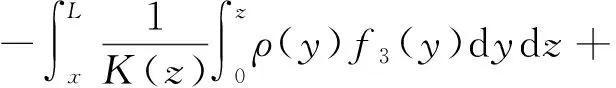
(15)

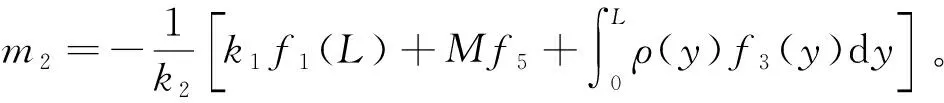
因此，由假设(2)及式(8)，式(12)，式(15)得到，存在某个正常数M>0，使得:

(16)

命题假设(2)成立，那么iR⊂ρ()，其中i为单位虚数。

证明由于具有紧的预解式，用文献[10]中引理4.1的类似方法得到：

{λ∈σ()| Imλ≠0}⊂σP()

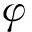
(iω-)(w,,v,ψ,ξ,η)=0

(17)

从而

0=Re〈(iω-)(w,,v,ψ,ξ,η),(w,,v,ψ,ξ,η)〉=-k1|ξ|2-k3|η|2

于是

ξ=0,η=0

(18)

由式(17)和式(5)，可得：

(19)

因此，由式(2)，式(4)，式(18)和式(19)，可得：

(20)

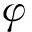
3 系统的的能量一致指数衰减估计

下面证明本文的主要结果，即系统的能量是一致指数衰减的。

定理2如果假设(2)成立，那么系统(1)的能量E(t)是一致指数衰减的。

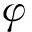
和

由于系统(1)的能量E(t)一致指数衰减等价于算子生成的压缩C0-半群et的一致指数稳定性。由命题和频域结果[11]，只需证明

(21)

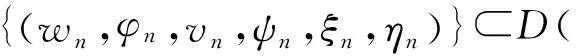
(22)

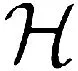
(iλn-)(wn,n,vn,ψn,ξn,ηn)=(f1n,f2n,f3n,f4n,f5n,f6n)→0

(23)

由式(23)可得，在V中，有：

(24)

在H中，有:

(25)

在C×C中，有:

(26)

(27)

为了证明定理2，需要用到下面引理。

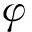
(28)

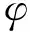
(29)

证明由式(23)和式(6)，可得：

Re〈(iλn-)(wn,n,vn,ψn,ξn,ηn),(wn,n,vn,ψn,ξn,ηn)〉=k1|ξn|2+k3|ηn|2→0

从而

ξn=vn(L)→0,ηn=ψn(L)→0

(30)

由式(30)结合式(24)，可得：

n→∞。

又由式(24)可得式(29)，引理4得证。

接下来继续证明定理2。由式(24)可得，f1n(L)→0,f2n(L)→0，且在L2(0,L)中，有：

f′1n-f2n→0,f′2n→0

(31)

因此由式(25)可得，在L2(0,L)中，有：

f3n→0,f4n→0

(32)

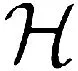
(33)

(34)

由式(33)和式(34)相加，同时取得实部，可得：

(35)

这样，式(35)结合式(22)，式(29)，可得：

(36)

为了得到矛盾的结论，只需证明，在L2(0,L)中有：

(37)

由式(24)和式(25)，可得：

(38)

(39)

取乘子h(x)=eμx-1，其中μ是后面将要确定的正常数。

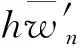
(40)

再由式(40)分部积分并取实部，可得：

(41)

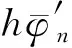
(42)

再由式(42)分部积分并取实部，可得：

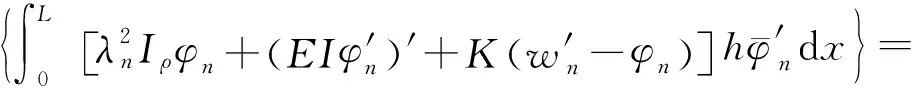
(43)

将式(41)和式(43)相加，可得：

(44)

因为正常数μ的存在性由假设(2)保证。所以能够选择到足够大的μ和正常数C>0，使得

(45)

因此，式(44)结合式(45)，在L2(0,L)中，可得：

(46)

由式(29)和式(46)，可得：

(47)

从而得到式(47)和式(36)矛盾，定理2证毕。

4 结束语

本文研究具有动态边界Timoshenko梁的线性反馈稳定性，借助线性算子半群理论结合乘子方法得到相应的稳定性结果。如果在动态边界上施加的线性反馈阻尼换成粘性阻尼或分数阶弱阻尼，会产生什么样的结果？会以什么方式稳定?将在以后的研究中不断探索。