农业领域离散元法（DEM）参数标定现状与发展

吴正阳，谢方平,2※，梅玉茹，王修善,2，刘大为,2，邬 备,2

（1.湖南农业大学机电工程学院，长沙 410128；2.智能农机装备湖南省重点实验室，长沙 410128）

引言

离散元法（DEM）是一种将介质整体视为若干颗粒单元集合的数值模拟方法，利用牛顿第二定律和接触模型，以每个颗粒的运动学和动力学行为描述整体特征。从1979年提出至今，ITASCA公司开发的PFC-2D/3D、DEM Solution公司推出的EDEM、ESSS公司研发的Rocky-DEM、开源LIGGGHTS、ESyS-Particle等DEM软件为DEM的广泛应用奠定了基础。

DEM已被广泛应用于葡萄和玉米脱粒[1,2]、玉米和水稻清选[3-6]、土壤与农机具相互作用[7-15]等农业领域。由于农业物料外形各异、尺寸不一，农田土壤粒度分布复杂、孔隙度不均匀，DEM模拟的物料外形尺寸或土壤粒度和孔隙度存在一定的误差。该误差会导致仿真对象的物理特性与实际情况存在较大差异。为在DEM中再现研究对象的实际物理特性，需要确定合理的DEM参数以弥补差异。因此，DEM参数标定是DEM准确仿真的重要前提，也是大部分DEM仿真研究的重要组成部分。

DEM相关的文献出版数量呈指数式增长[16]，而其中只有小部分涉及详细的DEM参数标定方法[17]，且有关详细的DEM参数标定文献大都出自南非Stellenbosch大学机电工程系的 Corné Coetzee[1,19-28]。大部分与DEM仿真研究相关的文献没有提及如何获得参数[3-5]或者直接引用其他来源的参数[8,10,11,15,29]。

当前DEM接触模型发展迅速[12,30,31]，但与模型对应的接触参数的系统化标定方法发展相对缓慢，在一定程度上影响了DEM仿真研究的发展。通过总结近10年国内外研究采用的不同标定流程以及标定方法，从选择接触模型、参数获取方法、颗粒建模、标定实验与仿真试验等方面，分析和讨论目前应用于农业领域的DEM参数标定方法，为研究人员未来改进或开发标定流程奠定基础，并为开发更加系统化的且能经过实际应用验证的标定方法提供有价值的参考。

1 选择接触模型

选择合适的接触模型是DEM仿真的重要前提。DEM接触模型是一种基于胡克定律的计算方法，用于描述相互接触颗粒间的力学变化规律。依据不同的研究对象或不同的研究目的，适用的接触模型有所不同，而不同的接触模型输入的参数也有所不同。以EDEM_v2018软件为例，常用的接触模型输入参数及其适用范围如表1所示。

表1 EDEM中常用接触模型输入参数及其适用范围

2 参数获取方法

2.1 直接测量方法

直接测量方法是直接测量接触水平的参数，例如静摩擦系数和滚动摩擦系数。Ucgul等[32]利用如图1所示的斜面试验测量沙-钢的滚动摩擦系数。其中，钢球是直径为18.98mm质量为28g经过抛光处理的40号钢，沙盘是装有压实平整沙子的托盘。该试验通过缓慢增大沙盘倾斜角，获得钢球刚开始滚动时的倾斜角ε，再由式（1）计算沙-钢的滚动摩擦系数。

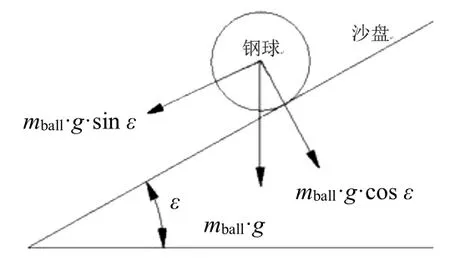
图1 斜面试验示意图[32]

式中，rμ是沙-钢滚动摩擦系数；ε是钢球刚开始滚动时沙盘的倾斜角。

Barrios等[33]通过如图2所示的自由落体试验测量铁矿石-铁矿石、铁矿石-钢和铁矿石-橡胶之间的恢复系数。使单个铁矿石在真空中自由下落，通过高速摄影分别捕捉碰撞前后5帧的图像估算碰撞前后速度（v0和v′），最后由v'/ v0计算得恢复系数。

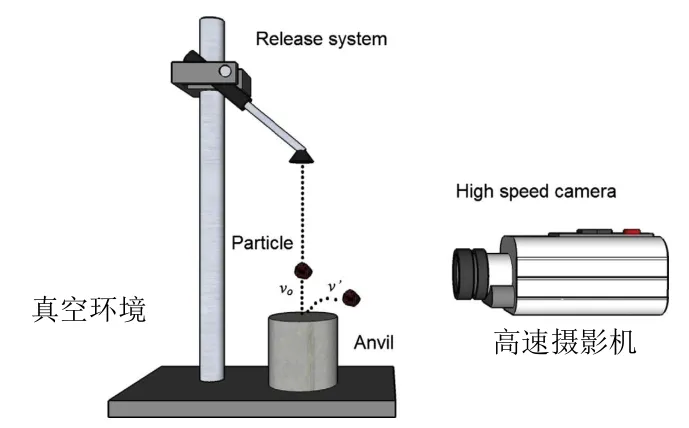
图2 自由落体试验[33]

郑侃等[8]利用MXD-01型摩擦系数测量仪测量不同土层颗粒与破土刃之间的静摩擦系数和滚动摩擦系数，贺一鸣等[34]用比重瓶法测量土壤的密度，González-Montellano等[35]同样使用比重瓶法测量玉米和橄榄的密度。

诸如密度、摩擦系数、恢复系数等参数可以直接测量，而要测量类似Edinburgh Elasto-Plastic Adhesion（EEPA）模型定义的范德华型恒定拉脱力可能比较困难，该模型定义的塑性变形比、表面能和切向刚度因子甚至无法直接测量。因此，直接测量法的应用有一定局限性。

2.2 批量标定方法

批量标定方法是利用实地测量或实验室实验方法测定特定物料的物理特性，再遵循实验室或实地测量的设置和步骤，并在仿真中模拟实际情况，然后迭代更改DEM参数值，直到仿真的整体响应与实际测量结果匹配。这个迭代更改的过程又可以细化为基于经验法的直接调整参数、基于优化算法的参数寻优、基于响应面法的试验设计等。

直接调整参数方法一般不涉及参数获取过程，通过调整DEM参数直至仿真的物理特性与实测情况匹配。Ucgul等[32]通过直接调整仿真时间步长、颗粒间静摩擦系数和滚动摩擦系数，实现仿真试验中的休止角和能量-贯入深度曲线与实验室测量情况基本相同。Janda和Ooi[31]直接调整EEPA模型参数，使仿真试验的无侧限抗压强度与实测的无侧限抗压强度呈现良好的一致性。

优化算法的参数获取方法，通过揭示研究的物理特性与DEM参数之间的映射关系，并通过这种映射关系找到最接近实际情况的参数组合。苑进等[36]通过参数敏感性分析，得到对掺混均匀度影响显著的参数是颗粒-传送带的静摩擦系数、滚动摩擦系数和颗粒间的滚动摩擦系数。利用相关向量机（RVM）揭示这3个参数与掺混均匀度的映射关系，并以平均相对误差为适应度函数，通过遗传算法（GA）对初始种群选择、交叉、变异直至种群平均适应度收敛于种群最大适应度，从而得到最大适应度的参数组合。Simone等[37]通过遗传编程（GP）对单轴压缩实验的敏感性参数进行标定。

响应面法的试验设计方法通过系统地调整参数并重复试验，拟合试验结果与参数之间的多项式函数，并通过多项式求解符合实际情况的最佳参数组合。贺一鸣等[34]以JKR表面能、颗粒-颗粒静摩擦系数、滚动摩擦系数和恢复系数为试验因素，休止角为响应，按照二次正交旋转组合设计3中心点的试验，得到上述参数与休止角的归回模型。以实测休止角为目标得到最终参数组合，其仿真休止角与实测休止角基本一致。李俊伟等[37]以休止角为参考，利用基于响应面法的Box-Behnken试验设计得到颗粒间JKR表面能、静摩擦系数、滚动摩擦系数和恢复系数对休止角响应的二次回归模型，获得类似的结果。王宪良等[29]利用类似的方法获得与实测休止角、黏聚力和内摩擦角匹配的颗粒半径、颗粒间静摩擦系数和滚动摩擦系数。

2.3 方法小结

对于直接测量方法，摩擦系数、恢复系数、剪切模量等参数比较容易测量，细观参数的测量则比较困难，数值化的参数甚至无法直接测量。再者，颗粒形状、尺寸和接触方式的高度理想化决定了即使可以直接准确地测量所有参数，也不一定意味着建立的DEM模型会显现相同的整体性能。对于批量标定方法，直接调整参数满足一个以上条件是比较难实现的，响应面法的试验设计次数会随着输入参数的增加而急剧增加，优化算法的计算成本也会随之剧增。因此，通过简单的直接测量确定一部分输入参数，再对剩余输入参数进行批量标定是一种节约研究成本、提高工作效率的有效手段。

3 颗粒建模

在进行标定实验和仿真试验之前，除了选择合适的接触模型，确定适宜的参数获取方法，还应谨慎考虑研究对象的形状和粒度分布。在大多数DEM软件中，设定离散颗粒的基本单元为球体，因为球形颗粒有助于高效检测和判断接触，且不用考虑方向。研究表明[39]，非球形单元的计算成本是球形单元的2至3倍，甚至是10倍。本文中讨论的是以3D球体为基本单元的颗粒建模，不包括2D圆盘。

3.1 颗粒形状

农业领域的DEM研究对象形状各异。由多个球形颗粒组合成团块，是目前DEM研究人员表征各种形状的常用方法。该团块由两个或多个球形颗粒刚性连接而成，球形颗粒可以在任何程度上重叠且相互之间不会产生接触力，仿真过程中团块不管受力如何都不会破裂[40]。大多数DEM仿真研究不会提及具体的颗粒形状建模过程，少数研究人员对比了不同颗粒形状产生的影响。

Markauskas等[41]分别使用如图3所示的4、6、8和12个球形颗粒组成的轴对称团块模拟玉米料仓卸料的过程，通过调整团块颗粒的密度以达到相同的质量，并与实际测量结果进行比较。结果表明，如果这4种团块都使用相同的接触参数，那么随着颗粒数的增加，卸料速率也会随之增加。通过调整4种颗粒间的摩擦系数可以使得每种团块模拟的卸料速率都相同。

图3 使用4（a），8（b）和12（c）个球形颗粒组合的玉米籽粒[41]

当研究对象形状近似球形或椭球时，为减少仿真时间和建模难度，将近似球形或椭球的物料简化为球形颗粒或球形单元组成的椭球团块是一种常见的办法。Markauskas和 Kaˇcianauskas[42]使用如图4所示的不同数量球形单元组合且长短轴比分别为1.5、2.35、5和10的椭球团块，用于模拟稻米休止角试验。在进行休止角对颗粒间静摩擦系数（0.1-1.0）和滚动摩擦系数（0-0.3）的敏感度分析过程中发现：在滚动摩擦系数小于0.3的情况下，即使采用1.0的静摩擦系数，不论是何种形状颗粒的试验休止角都无法达到实测的35°；当滚动摩擦系数设为0.3时，采用0.4左右的静摩擦系数，每个形状颗粒的试验休止角都可以达到实测休止角。

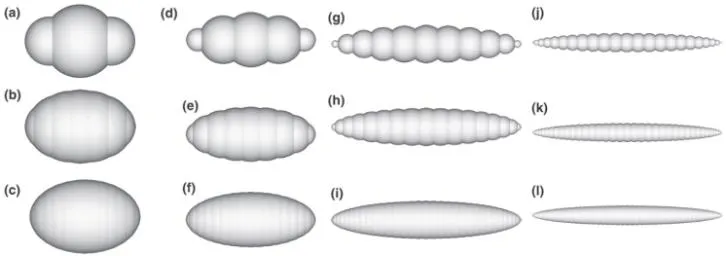
图4 不同长短轴比和不同球体数量的椭球稻米颗粒[42]

研究对象近似于球体或椭球，其与DEM中理想化的球形椭球形颗粒在内部流动方面仍有显著差异。因此，在将颗粒模型简化为轴对称的椭球或球形时，摩擦系数的物理意义损失较大。李俊伟等[37]将粘土颗粒简化为球形颗粒进行休止角的标定实验，在最终的标定结果中静摩擦系数达到0.78和0.80，在贺一鸣等[33]的标定结果中静摩擦系数达到1.06，更加验证了文献[42]的结果。

农业物料（例如果实和种子）的形状建模最常用的方法是将其模拟成球形颗粒或球形颗粒组成的团块[43]。谷物收获后流程（例如清选和卸料）的物料建模取决于特定的谷物和实际工况。针对诸如稻谷、小麦、玉米等非球形物料，一般采用团块模拟[44]。使用团块模拟物料时，颗粒形状建模至关重要。目前对颗粒形状进行详细标定的研究比较少见。大多数研究人员在使用团块颗粒时没有交待详细的建模过程或者只简单对比了不同形状物料的特性[27]。像大豆和油菜这种近似于球形的物料，用单个球形颗粒模拟可能更加准确。如果使用单个球形颗粒模拟非球形物料，那么（与用椭球模拟类椭球物料类似）有必要引入更大的摩擦系数限制其流动性。

3.2 颗粒尺寸

实验室规模的颗粒建模可能对粒度分布进行较精确的建模。对于某些大量颗粒建模（例如土槽建模，尤其是粒度分布测量困难、土壤结构复杂的农田土壤），按照实际粒度分布进行准确建模可能会有数以百万计乃至千万计的颗粒。由于一般难以接受如此巨大的计算成本，因此为降低计算成本，在仿真中可以增大粒径。目前国内外流行的可行方案有：保持模型域即几何体尺寸不变的同时增加粒径[32,35,37,43]；忽略尺寸小于某个特定值的颗粒[46-48]；按比例放大所有颗粒尺寸[47,49,50]。

Ucgul等[32]对无粘性、含水率为0.5%的沙滩沙进行参数标定。由于沙子颗粒较小，因此在仿真中使用半径在9.5～10.5mm范围内的颗粒。结果表明这种放大的颗粒可以预测耕作部件的受力情况。李俊伟等[37]利用休止角试验对不同含水率的黑粘土进行参数标定时，使用的颗粒半径在2～4mm的范围内。类似地，这种放大的颗粒再现了实测休止角。

Roessler和Katterfeld[51]利用提升法的休止角试验对加水的湿沙进行标定实验。传统的提升法休止角试验是典型无粘性物料的休止角测定方法。然而在对粘性物料进行标定实验时，发现提升空心圆柱后的物料并没有呈现出良好的锥形，测量的休止角在40.4°～84.3°之间。因此，在匀速提升圆柱的过程中，每当圆柱底面与落料平面间隙分别为80mm、100mm、120mm和140mm时，记录下20mm、40mm、80mm和120mm高度下物料的截面直径，并用定义的相对弯曲代替休止角，如图5所示。进一步对比缩小2.5倍尺寸的空心圆柱和8～100mm/s的提升速率，得到的结论为：相对弯曲与提升速度无关，在保持圆柱相同高径比的前提下与其尺寸也无关。因而在仿真标定试验中，使用相同高径比但所有尺寸都缩小2.5倍的空心圆柱。此外，由于沙粒太小，半径在5.5～12.7mm范围的球形颗粒被用于模拟沙粒。没有完全复制实际情况的粒度分布，标定后的结果仍然与实测值呈现良好的一致性。这与文献[52]的结论相似。

图5 提升过程中测量指定高度的截面直径[51]

Feng等[47]开发了基于三个相似性原理（几何体相似性、力学相似性和动力学相似性）用于离散元颗粒系统的缩放定律。其研究结果表明：如果颗粒间作用力-重叠量具有以下式（2）所示一般形式，且α与β满足以下式（3）所示条件，则保持力学和动力学条件不变并以相同的比例因子缩放几何体尺寸，仿真中的结果具有尺度不变性（不论缩放比例如何，结果都会保持不变）。

其中：k为接触刚度，r为颗粒平均半径，δ为重叠量，α与β均为常数。

其中：nd是常数，二维空间中为2，三维空间中为3。

由式（2）和式（3）可见，线性接触定律就是当α和β同时为1的情况下，仅在二维空间中仿真结果具有尺度不变性。三维空间中线性接触定律就是当α为2和β为1的情况下，如果要满足尺度不变性，那么应使用与粒度缩放因子成反比的乘数将接触刚度k进行缩放。此外，根据该文献的描述，如果几何体保持未缩放比例，也就是未保持几何相似性，将导致取决于缩放因子的建模误差。

Obermayr等[50]证明了Feng等[47]的理论，应用α为1/2和β为3/2的三维非线性接触定律，将几何体按照相同的比例因子缩放，进行颗粒半径分别为3mm，30mm和300mm的三轴压缩试验。试验结果表现为3组试验的应力-应变曲线具有良好的一致性，如图6所示。表明三维非线性接触定律的模型具有尺度不变性。

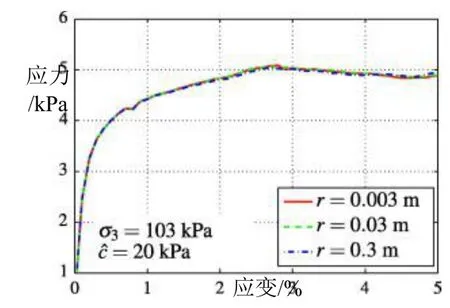
图6 不同粒径的应力-应变曲线[50]

4 标定实验与仿真试验

选择合适的接触模型，确定适宜的参数获取方法，针对研究对象建立颗粒模型，还应根据工况进行标定实验和仿真试验。国内外研究人员依据研究工况，利用休止角和土壤-触土部件相互作用[28,32,34,37,51-53,62-72]、直剪切试验[28,29,53-60]、压缩试验[61,62]等对DEM材料参数（泊松比、颗粒半径、剪切模量等）和模型接触参数的标定提出了诸多方法。

4.1 休止角和土壤-触土部件相互作用

休止角（Angle of repose）是反应物料流动性的重要指标，国内外学者常用的测量方法如图7所示。其中：注入法是指将物料从一定高度的漏斗均匀注入到圆盘中，直到圆盘上形成稳定的锥形体，测量锥形体底角作为休止角；排出法是指将物料填充在圆筒中，然后匀速提升圆筒，测量形成锥形体的底角作为休止角，或者将物料填充至方盒中，通过撤去方盒的一个侧面排出物料，测量物料排出后形成的斜坡角作为休止角；倾斜角法是指将物料填充至托盘中，缓速倾斜托盘，把物料处于刚好不下滑状态下的倾斜角视为休止角；转动圆筒法（Rotating drum）是指将物料置于密封圆筒中，通过匀速转动圆筒，测量圆筒中形成的倾斜角作为休止角。针对同种颗粒材料，采用不同测量方法获得的休止角也会存在差异。

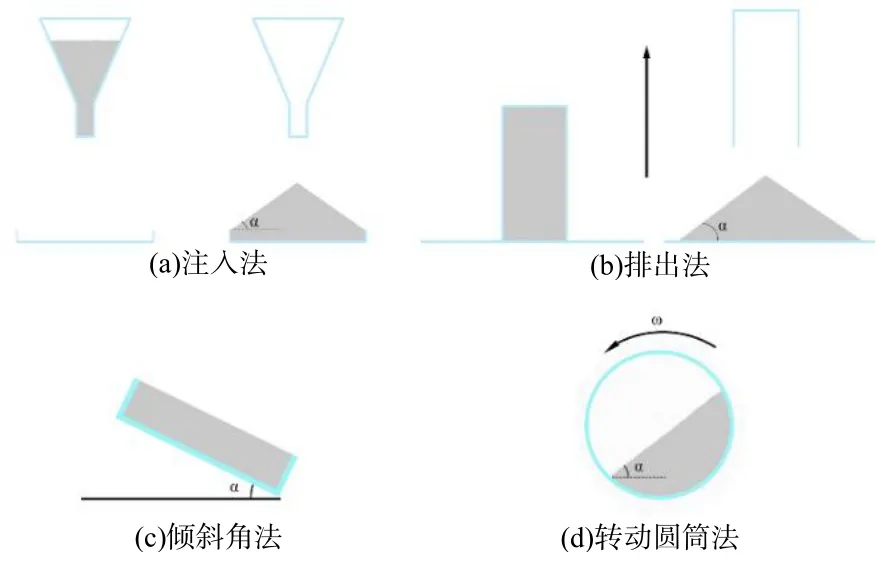
图7 常用休止角测量方法

贺一鸣等[34]以注入法测量的休止角为参考，在仿真中遵循实际实验设置和步骤，利用基于响应面法二次正交旋转组合试验设计得到颗粒间JKR表面能、静摩擦系数、滚动摩擦系数和恢复系数对休止角响应的二次回归模型，并以实测休止角为目标对上述4个参数进行标定。李俊伟等[37]使用类似的方法进行标定实验。Combarros等[53]利用转动圆筒法测量休止角，在仿真试验中发现颗粒间滚动摩擦系数和静摩擦系数是休止角的敏感性参数，而单个实验参考不足以确定这两个参数。因此将排出法的休止角加入其中，以转动滚筒和排出法测量的休止角为目标确定了上述两参数。刘凡一等[63]采用排出法测量小麦的休止角，并对颗粒间静摩擦系数、滚动摩擦系数和小麦-有机玻璃静摩擦系数进行标定。

另外，不少学者在进行基于休止角实验的DEM参数标定中发现：颗粒间静摩擦系数和滚动摩擦系数是影响休止角的主要因素[28,51-53,69-72]。这可能为休止角实验的参数标定节约参数敏感性分析的环节。

Mak等[66]对土壤-触土部件相互作用进行研究，确定建模粘性土壤所需的颗粒间法向刚度、切向刚度、摩擦系数、粘结法向刚度、粘结切向刚度、粘结法向强度、粘结剪切强度、粘结键半径系数、局部阻尼系数和粘性阻尼系数。只对颗粒间的法向刚度进行标定，其他参数均取自文献。在标定法向刚度过程中，没有进行独立的标定实验，而是将与实际实验相同外形尺寸和相同行进速度的仿真叶片分别作用于5个由不同法向刚度颗粒组成的土壤模型，通过对比叶片水平、垂直方向的阻力和土壤扰动宽度与McKye公式[67]预测值的误差，将这3个误差平均值最小情况下的颗粒法向刚度作为标定值。Li等[15]采用完全相同的方法获取颗粒间法向刚度，如图8所示，不同的是将叶片水平、垂直方向的阻力和土壤扰动宽度与UEE公式[68]预测值进行比较。文献[15,66]均未与实际实验进行比较。

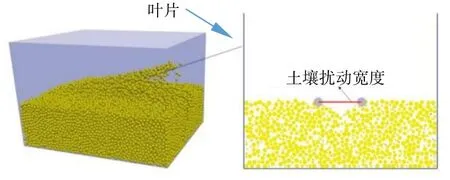
图8 叶片入土试验[15]

Ucgul等[32]在标定实验中进行如图9所示的圆盘和圆锥贯入阻力试验，通过直接调整法使得仿真的能量-贯入深度曲线与实际情况匹配。

图9 贯入阻力试验与标定结果[32]

4.2 直剪切试验

Karkala等[54]使用来自文献[55]的DEM参数在EDEM软件中建立一个无侧限抗压强度（动态屈服强度）试验和直剪切试验的对照试验。之后，又在这个对照试验的基础上使用10倍的剪切速率，并将该试验结果与对照试验结果对比发现：加速剪切状态下，剪切应力确实更早地达到临界值，而临界剪切应力并未有显著变化。该结果表明提高剪切速率是缩短仿真剪切试验时间的有效办法。在仿真的无侧限抗压强度试验中，压缩后的试样（直径25mm、高25mm的圆柱）被去除限制壁，顶板以100mm/s的恒定速率（应变率=4s-1）下压直至试样失效。期间记录顶板的压力和试样端面的变形，并将压力换算为压应力。分析发现JKR表面可能是无侧限抗压强度的极敏感参数。通过“试错法”（在参数的可行域内等分若干组并逐一尝试），选取一组与实测值误差最小的JKR表面能参数。在这项研究中并未与实际实验进行比较，4s-1的应变率是否与实际情况差异较大，也没有像使用10倍剪切速率那样验证应变率是否会对最终的峰值压应力有显著影响。

王宪良等[29]结合直剪切试验和排出法的休止角试验，分析休止角、黏聚力和内摩擦角对颗粒密度、半径、泊松比以及颗粒间表面能、法向刚度、切向刚度、剪切模量、静摩擦系数、滚动摩擦系数和恢复系数的敏感度。结果表明休止角、黏聚力和内摩擦角对颗粒半径、颗粒间静摩擦系数和滚动摩擦系数的敏感度都比其他参数高出一个数量级。因此，利用响应面法可得到这3项参考与3个主要参数的回归模型，优化求解可得到唯一的参数组合，即颗粒半径、颗粒间的静摩擦系数和滚动摩擦系数分别为5.7mm、0.45和0.21。在试验中，并未对该特定模型定义的接触参数进行标定，所有接触模型参数均取自其他文献；利用轮胎-土壤接触面应力验证了参数的准确性。在验证过程中，没有将该参数组合的仿真值与实测值进行对比，而是将模型预测值与实测值进行比较。根据文献[27]，离散元参数标定的最终目的是使得标定的参数组合能应用于实际，而不是为了与设计的标定试验匹配。

4.3 压缩试验

Li等[61]利用一系列的二维双轴DEM模拟，通过改变接触法向刚度、接触切向刚度和接触滑动摩擦系数来找到响应面系数。对于给定的围压和载荷步，求解7个方程，可以找到7个响应面系数。在给定的围压和10个加载步骤中的每一个加载下，法向刚度、切向刚度和摩擦系数与总体偏应力相关。使用优化算法，可以最小化被测应力和预测偏应力的均方根值，以找到最适合给定围压的测量数据。结果表明，法向刚度和切向刚度大致相同，且在所有情况下的差异均小于5%；摩擦系数在0.92至1.04之间变化。如果要考虑颗粒形状，则必须增加滑动摩擦系数，并且该摩擦系数很可能会高于两个物理颗粒之间的测量值[62]。结果还表明接触刚度和摩擦系数随着围压的增加而增加，证明参数和试验参考值取决于应力，应仔细选择在标定实验中使用的应力水平。

4.4 其他试验

Roessler等[17]针对同一种干粗砾石进行落料箱试验，如图10所示。目的是为了对颗粒间的静摩擦系数和滚动摩擦系数进行标定。每种试验重复三次并将测量误差考虑在内，这样对应每个参考的参数可行解在等高线图上就不是单条曲线而是误差范围内的可行域。将排出法和注入法休止角的可行域叠加，发现重叠部分比任何单独参考值的可行域都要小很多，得出使用单个参考标准的标定试验不足以确定可行解的结论，与文献[53]的结论相似。此外，还将能匹配落料箱试验中下部箱体排出质量、落料孔平均质量流率和排出法的休止角参数可行域叠加，得到比之前更小的可行域。因此，单独的落料箱试验可获取多个参考，且在考虑测量误差的前提下能有效减少可行解的数量。

图10 落料箱试验

李俊伟等[37]利用斜面试验，即将3D打印的半径为5mm的土粒分别静置在相同倾斜角的65Mn和PTEF材料表面，使其从同一高度自然滚下，测量土粒的水平滚动距离，对触土部件与土壤间的JKR表面能、静摩擦系数、滚动摩擦系数和恢复系数进行标定。在该研究中，即使是3D打印的球形土粒也存在一定的孔隙，也就是说这个土粒的堆积密度固然小于土壤的真实密度，而用于斜面试验仿真的颗粒密度是如何定义的无从知晓。土壤与触土部件的相互作用，不应是单个土粒与部件的相互作用，而应是触土部件作用于土壤颗粒群时，部件对颗粒群整体的宏观响应或某些力学方面的变化，或者是土壤颗粒群作用于触土部件时，颗粒群对部件的作用效果。采用离散元法，本质上是利用各个离散元素表征研究对象的整体运动规律。这种将物料颗粒模型简化的方法一般是可取的[74,75]，而为简化模型将实际土壤制作成球形颗粒略显得不合时宜。3D打印球体的球面度也可能成为影响滚动距离的主要因素，不同打印精度的土球滚动距离差异可能较大。斜面试验适用于直接测量颗粒与材料的静摩擦系数或滚动摩擦系数[28,62-65]。

5 发展与建议

获取DEM参数是DEM仿真的重要内容。虽然有关参数标定的研究发展迅速，但仍存在一些亟待解决的问题。为推动参数标定方法的改进与创新，提出以下建议：

（1）DEM待输入参数众多，为简化参数获取过程，一般应将批量标定方法与直接测量法配合使用，例如标定之前直接测量材料的密度、泊松比、剪切模量、摩擦系数等。农业物料外形各异、尺寸不一，农田土壤粒度分布复杂、孔隙度不均匀。DEM模拟的物料外形尺寸或土壤粒度和孔隙度存在一定的误差。由于该误差会导致仿真对象的物理特性与实际情况存在较大差异，因此不建议完全使用直接测量法。

（2）农业物料形状各异，将多个球形颗粒组合成团块是目前DEM研究人员表征物料形状的常用方法。使用这种团块的优点在于其表面仍是多个球面的组合，接触检测和判定仍然与球形颗粒相同。也正是因为这种球面的组合决定了要精确建模物料的尖锐边缘和光滑表面就需要大量的球形颗粒，这就大幅度增加工作量和仿真时间。因此，有必要将颗粒形状建模作为一种DEM参数。大多数研究中不会提及详细的形状建模过程，系统化的形状建模方法仍然匮乏。在颗粒碰撞、内部流动等与颗粒形状密切相关的研究中，颗粒形状建模十分重要。一旦对某种颗粒形状的DEM参数进行标定，该接触参数可能只适合该形状的颗粒。因此，在调整建模形状时，也应对DEM参数进行调整或重新标定。

（3）在不考虑颗粒形状影响的情况下，简化颗粒模型是一种常用手段。例如使用球形颗粒组成的椭球模型模拟稻米和小麦，使用球形颗粒模拟土壤颗粒、油菜籽粒、大豆籽粒等。研究对象即使非常近似椭球或球形，也与DEM中理想的椭球或球形在内部流动性方面与实际情况有较大差异。由于使用较大的摩擦系数可限制这种流动性，因此在参数标定之前，建议选择较大的摩擦系数范围。

（4）只对敏感参数进行标定，是国内外学者常用的方法。在这种情况下，对非敏感参数的确定存在一定的不确定性。目前，除JKR等定义参数较少的接触模型以外，模型全部接触参数的标定方法鲜有报道。例如，EDEM软件内置的EEPA接触模型定义的参数加上滚动摩擦系数、静摩擦系数和恢复系数，共有9个建立模型所需的接触参数。由于目前可接受的待标定参数至多4个，因此对多参数模型的全参数进行标定具有一定挑战性。

（5）不论参数标定流程如何，在标定结束时都需要提供一组参数组合。仿真试验的整体响应（如休止角）往往受一个以上参数的影响，这就意味着回归模型至少是二元的。在大多数标定过程中，仅考虑单个响应获取的参数组合一般不是唯一的。在选择最终的一组参数组合时，这种模糊性将不利于DEM参数标定程序的研发。为减少可行参数组合甚至获得唯一的参数组合，建议在单个实验中获取多个与研究相关的参考值，或进行多个标定实验。

（6）标定实验和仿真试验的力学和动力学条件应该保持一致，在不得不改变该条件之前，应分析变化的力学和动力学条件对试验结果的影响。

（7）参数标定的最终目的不仅是为了使标定的参数能匹配实验室结果，还要与实验相关的实际应用结果相对应。例如，匹配实验室测量休止角的DEM参数，还应匹配开沟实验的沟型。因此，为验证标定方法的实用性，建议除了进行实验室规模的验证外，还应进行实际应用的验证。

6 结论

农业物料外形各异、尺寸不一，农田土壤粒度分布复杂、孔隙度不均匀，DEM模拟的物料外形尺寸或土壤粒度和孔隙度存在一定的误差。因此，为在DEM中再现研究对象的实际物理特性，需要确定合理的DEM参数以弥补误差。分析、总结了目前常用的直接测量方法和批量标定方法。直接测量法可用于直接测定颗粒密度、剪切模量、接触刚度、滑动摩擦系数、恢复系数等，其优点为测定的参数在不同的软件下或不同的接触模型中均可受用，其缺点为在颗粒尺寸较小或形状复杂的情况下，测量工作将很难展开。在颗粒形状、尺寸和接触方式高度理想化的情况下，精确测量参数值也很可能导致整体性能与实际情况存在较大差异。批量标定方法的优点在于不需要精密的仪器测量颗粒级或接触水平的参数，只需测量一项或多项整体性能指标。缺点就是重复地进行仿真试验非常耗时，有时一次试验获得参考数量不足以获取更少甚至唯一的参数组合。为简化标定流程，一般应将批量标定方法与直接测量方法结合使用。颗粒形状和粒度分布也应被视为DEM参数。在研究颗粒碰撞、流动性等情况下，不应忽略形状和粒度的建模过程。标定实验结果应与研究目的对应。此外，仿真试验应遵循标定实验的设置和步骤。

从接触模型选择、参数获取方法、颗粒建模、标定实验和仿真试验方面，陈述和讨论了农业领域DEM参数标定现状，并提出了几点建议，有助于未来研究人员改进或开发标定流程，为更加系统化且经过实际应用验证的标定方法开发提供有价值的参考。