对杆影变化规律确定时间及地点的研究

安云鹏 岳昊 董威

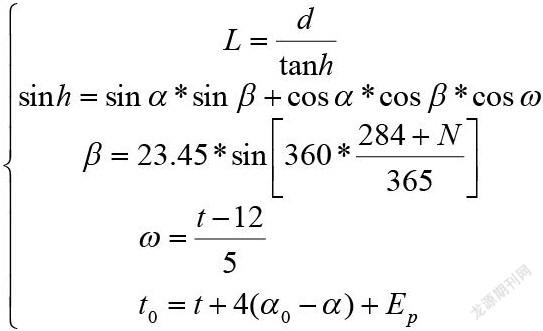
摘要：如今，人工定位方法多种多样，如GPS、北斗系统，但相对于复杂且昂贵的卫星技术，利用太阳影子定位则成为行之有效的方式，所以视频、图片的数据分析对于影子定位有无可替代的意义。我们团队利用Matlab软件对视频和数据进行提取和拟合处理，建立影子长度—太阳高度角模型，用来依据图片和视频甚至数字准确定位出相应的地理位置。就问题一而言，影长的变化受地点、时间、杆长、日期影响，采用控制变量法，以太阳高度角做媒介，建立影长与参变量函数模型，针对于每一个变量控制相应的参数，从而利用Matlab画出对应的函数图像，找出相应的变化规律。

关键词：控制变量法;最小二乘法;非线性拟合;灰度处理

1问题背景

随着智能化时代的到来以及智能手机的普及，人们越来越青睐于智能手机中的智能相机的视頻数据分析技术可以确定视频的拍摄地点和日期。通过研究太阳影子与定位之间的关系将会对确认拍摄的地点、日期有着至关重要的意义。

该模型以建立影子长度变化的数学模型，画出2015年10月22日北京时间9：00-15：00之间天安门广场北纬39度54分26秒，东经116度23分29秒3米高的直杆的太阳影子长度的变化曲线。通过时间与影子长度的变化关系，分析出时间与影子长度关于各个参数的内在变化规律。并通过建立影子长度变化的数学模型。

2模型建立与求解

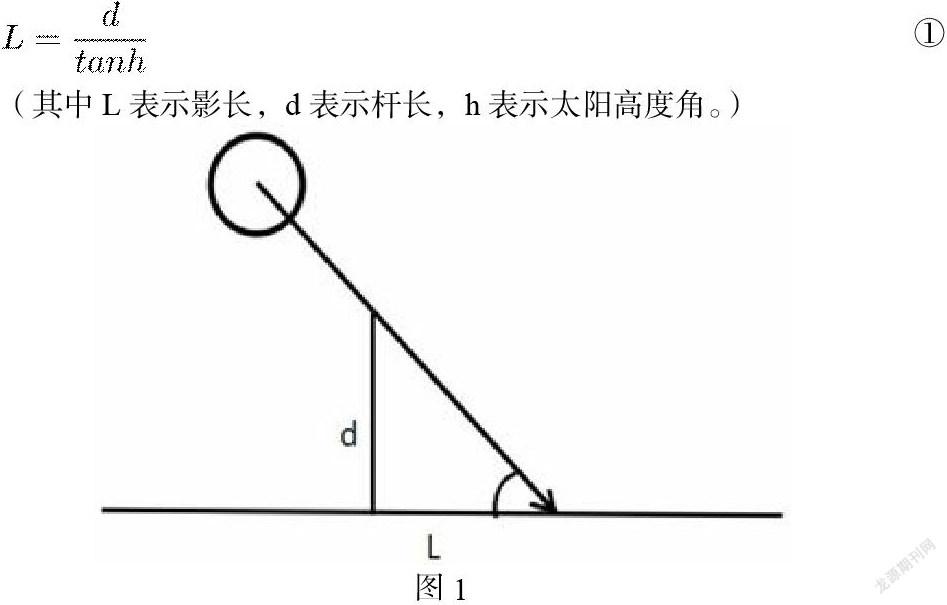
根据我们所掌握的资料可总结出直杆高度、影长和太阳高度角三者之间具有一定的几何关系，由此可列出公式

太阳高度角：

对于地球上的某个地点，太阳高度角是指太阳光的入射方向与地平面之间的夹角，是指某地太阳光线与通过该地与地心相连的地表切面的夹角。太阳高度角随太阳赤纬和时角的变化而变化，其计算公式为：

则欲求得太阳高度角乨，需求得太阳赤纬β和太阳时角ω

太阳赤纬是地球赤道平面和太阳与地球中心的连线的夹角，即太阳直射点的纬度值。太阳赤纬以年为周期在的范围内移动，成为季节的标志。因赤纬日变化很小，一天内赤纬变化产生误差忽略不计，所以一年内任何一天的赤纬将可用下式计算：

（其中的单位为弧度;pi=3.1415926为圆周率;③，4p单位为弧度。N为日数，自每年1月1日开始计算）。

3.时角

时角是指天子午圈与天体的赤经圈在北极所成的球面角，或在天赤道上所夹的弧度。日出和日落时时角最大，正午时角最小为0。从正午算起按顺时针方向为正，逆时针方向为负，即上午为正下午为负。时角的数值等于据正午的时间（以小时为单位）乘15°。则其计算公式为：

④（其中t表示地方时）

4.地方时

地方时是指按本地精度测定的时刻，地球表面精度每隔15°，地方时差一小时，地方时与所给的标准时（北京时间）的关系可以表示为： t0=t+4（α0-α）+ Ep⑤（其中t0表示北京时间，α0表示北京所在经度，Ep表示真太阳时时差数值对本模型影响不大可忽略。）由①②③④⑤关系式整理可得，我们可建立影长与杆长、观测地纬度、杆所在经度、日期序数以及北京时间之间的关系的模型：

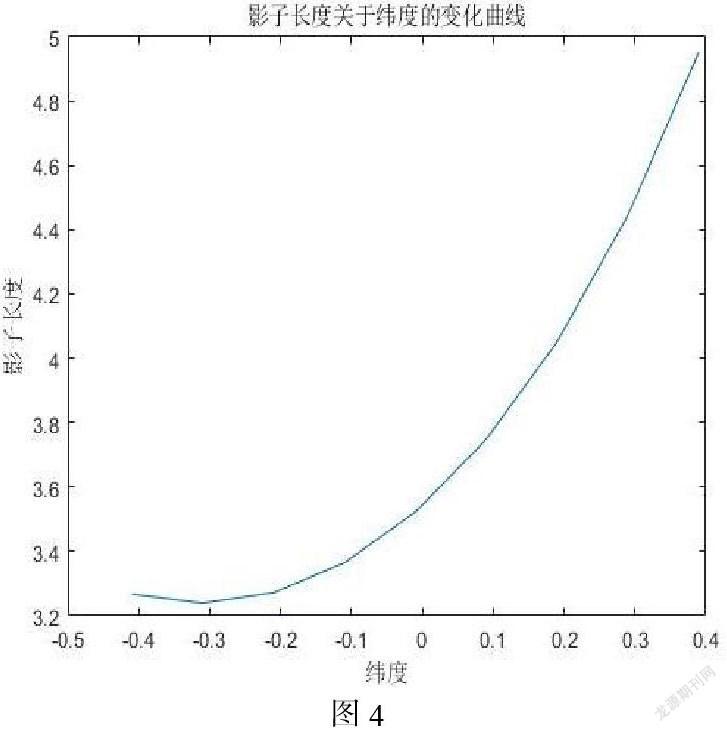
利用MATLAB进行计算从而确定杆所在纬度、日期序数、时间为定量时杆长与影长之间的函数关系图：

由此可以得出：在同一天内随着维度的升高杆影子长度先缓慢减少后迅速增长，在赤道地区（00附近）杆影子长度与维度呈现出近线性增长趋势。

参考文献

[1]陈大亮.关于物影变化规律的探讨[J].地理教育，2004（04）：17.

[2]黄伟.日出日落的方位与地平杆影日变化分析[J].地理教育，2017（S1）： 109-110.

[3]凡宁宁.基于太阳高度角的影子定位模型[J].数学学习与研究，2018（03）： 145-147.