数形结合思想引入高中数学解题教学的实践分析
邵霞
作为一种非常重要的解题思想,数形结合思想是简化数学问题,有效解决某些数学问题的一个有效解题思想,非常适合那些抽象性、繁杂性等特性比较强的数学问题求解。在代数、函数以及解析几何部分数学知识教学中,教师都可以针对性选择适宜的例题,将数形结合思想在解题中的应用方法传授给学生,力求可以借助有效的解题指导及训练来使学生切实掌握运用数形结合思想求解数学问题的方法。
一、巧用数形结合思想,求解集合问题
在高中阶段数学知识体系中,集合是非常关键的组成部分,也是最基础的学习内容,需要学生必须牢固掌握。在高考数学考试中,集合问题也是必考题型之一。在求解集合问题过程中,如果可以指导学生灵活应用数形结合思想,那么可以准确地对其相关联系性进行描述,显著提高学生求解集合问题的有效性。特别是如果可以巧妙地应用数形结合思想,可以以方程或图形等更加直观的形式来表达数量关系,之后可以通过方程求解等方式来获取集合问题的求解答案。但是针对那些涵盖函数等数学知识在内的集合问题教学中,需要注意对整个解题过程进行持续性优化,力求灵活应用抛物线等图形及方程来求解相应集合问题。
解析:在对这道数学集合相关题目进行求解期间,如果直接按照常规的熟练关系确定方式来求解问题,那么可以将给定的2个方程组相应地合并为一个方程组,之后通过求解方程组即可得到本道题的答案。该种解题思路虽然也可以求解相应的答案,但是却会涉及到非常繁琐、复杂的求解过程,整体的解题效率低下。此时在求解这道数学集合问题过程中可以指导学生灵活地应用数形结合思想,将题干中所给出的集合M和集合N中给出的方程分别绘制出对应的图象,之后本道题的求解实际上就转化成了求解这两个函数图像的交点数量(通过绘图可知二者的交点为2个,所以可知其中总共包括2个元素)。基于该种数形结合思想的灵活应用,那么可以使他们高效地求解这道数学问题,不仅缩减了解题过程,相应的解题结果准确度也大大提升。
二、巧用数形结合思想,求解函数问题
函数是构成高中数学教学中知识框架的一个重要内容,相关的类型题也是高考数学试卷考试的重点与热点,并且可以同数列、方程、不等式等其他方面的数学知识进行有机结合,加之学生本身的抽象思维能力比较差,所以会增加相关问题的求解难度。通过指导学生在求解函数问题过程中有效、灵活地应用数形结合思想,那么可以将有关的抽象函数问题以直观、生动的图形形式展现出来,这样更有利于简化数学问题,降低求解数学函数问题的难度,大大提高了高中生求解数学函数问题的能力。
例2:已知方程在区间中具有多少个解?
解析:在求解这道函数问题期间,如果学生按照常规的手段化简给定的方程,即:,故可以简化为。如此一来,就可以确定本道题的正确答案为3个。虽然采取该种数学计算方法也可以求解出这道题,但是还需要进行简化方程来求解方程,计算工序比较多,所以也可能会因为疏忽问题而造成錯解问题。而如果可以指导学生运用数形结合思想来求解这道数学题,即首先在统一直角坐标系中绘制出给定方程两边的三角函数,那么可以通过仔细地观察相应的图形来快速确定彼此之间的交点为3个,这样就可以得到相应的结果为3个。
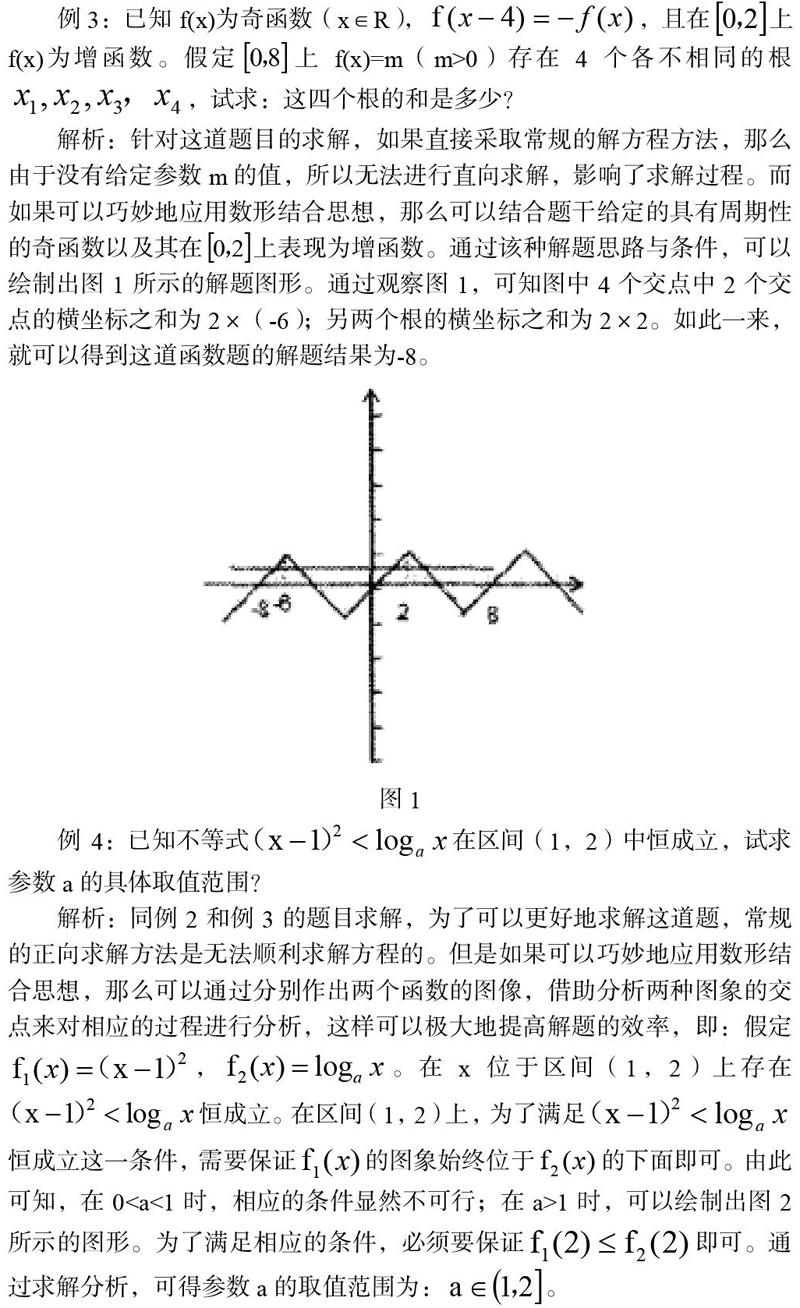
解析:针对这道题目的求解,如果直接采取常规的解方程方法,那么由于没有给定参数m的值,所以无法进行直向求解,影响了求解过程。而如果可以巧妙地应用数形结合思想,那么可以结合题干给定的具有周期性的奇函数以及其在上表现为增函数。通过该种解题思路与条件,可以绘制出图1所示的解题图形。通过观察图1,可知图中4个交点中2个交点的横坐标之和为2×(-6);另两个根的横坐标之和为2×2。如此一来,就可以得到这道函数题的解题结果为-8。
基于上述分析可知,在借助数形结合思想求解某些函数问题期间,如果给定的函数中包含未知参数,并且涉及到不等式或方程等条件,那么可以有效地运用数形结合思想来对求解的问题进行简化,保证可以更快速地求解问题,找到问题的正确答案。
基于上述解题分析可知,在求解几何问题的过程中如果可以灵活地应用坐标系来沟通数与形之间的关系,那么可以实现几何图形和代数之间的有机转化,这样可以起到简化待求解数学问题,提高学生求解问题效率的作用。
总之,数形结合思想是高中生需要掌握的一种求解方法,是提高我们求解数学问题能力中必不可少的一种数学思想。在初中数学解题中应用数形结合思想期间,可以结合函数问题、几何问题以及集合问题等不同类型题,灵活地运用数形结合思想来快速简化问题,保证可以有效提高高中生的数学解题能力。

