关于整函数的周期性研究

赵 莹， 孙桂荣

（苏州科技大学 数学科学学院，江苏 苏州 215009）

1 引言及主要结果

假设读者熟悉亚纯函数Nevanlinna 值分布理论的基本内容和相关符号[1-3]。 特别地，ρ（f）表示整函数f（z）的级，当ρ（f）＜∞时，称f（z）为有穷级整函数。

在复域微分方程方面，有很多学者研究了微分方程解的增长性、零点分布等[4-5]，而Eremenkot[6]发现周期性对Kuramoto Sivashinsky 方程的亚纯函数解表示有重要作用。这些都说明研究亚纯函数的周期性问题具有重要意义。然而，针对熟知亚纯函数与整函数之间的关系，笔者主要研究的是整函数的周期性。1978 年，日本学家Ozawa[7]就证明了存在大量周期整函数。

众所周知，任何以c 为周期的周期整函数f（z）都可以写成一个处处收敛的级数

Baker[8]证明了如果f（z）是一个非常数的整函数，而p（z）是一个多项式，且deg p（z）≥3，那么f（p（z））不是周期函数。 最近，关于整函数的周期性问题，有部分学者围绕着杨重骏提出的一个猜想进行了研究。

猜想1[9]假设f（z）是超越整函数，对某个正整数k，如果f（z）f（k）（z）是周期函数，则f（z）也为周期函数。

2018 年，王培和扈培础[9]证明了k=1 时猜想是正确的。

定理1 假设f（z）是超越整函数，对某个正整数k，如果（f2（z））（k）是周期函数，则f（z）也是周期函数。

随后，刘凯等人[10]研究了当f（z）有非零Picard 例外值时，猜想1 是正确的。

定理2 假设f（z）是超越整函数，d≠0 是f（z）的一个Picard 例外值，对某个正整数k，如果f（z）f（k）（z）是周期函数，则f（z）也为周期函数。

思考 猜想1 中研究的整函数f（z）f（k）（z）的形式与Hayman 猜想的其中一种形式f（k）（z）fn（z）相似，能在一定条件下得到f（z）是周期函数，故笔者想到Hayman 猜想的另一种形式f′（z）-afn（z），那么在一定条件下，是否也能推出f（z）是周期函数呢？

定理3 假设f（z）是有穷级超越整函数，0 为f（z）的一个Picard 例外值，如果f′（z）-afn（z）（n≥2）是周期为c 的函数，则f（z）=eaz+b，其中a，b≠0，并且eac=1，即f（z）是以c 为周期的周期函数。

问题1 如果f（z）有非零Picard 例外值，那么，定理3 的结论是否成立？

对这个问题进行了进一步的讨论，得到以下结论。

定理4 假设f（z）是有穷级超越整函数，d 为f（z）的一个非零Picard 例外值，如果f′（z）-afn（z）（n≥2）是周期为c 的函数，则f（z）=eaz+b，其中a，b≠0，并且eac=1，即f（z）是以c 为周期的周期函数。

2 引理

（2）当1≤k＜j≤n 时，gj（z）-gk（z）不恒为常数；

（3）当1≤j≤n，1≤h＜k≤n 时，T（r，fj）=o{T（r，exp（gh-gk））}（r→∞，r⊄E），其中E⊂（1，∞）是有穷的对数测度。

3 定理3 的证明

由于0 是f（z）的一个Picard 例外值，且f（z）是有穷级超越整函数，因此存在多项式p（z），使得f（z）=ep（z）且T（r，p（z））=S（r，f）。

因为f′（z）-afn（z）是周期函数，且周期为c，则

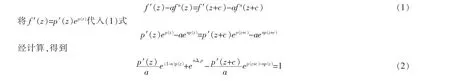
接下来，由引理1 对（2）式进行两种情况讨论。

情形1 deg p（z）≥2

由于e（n-1）（az+b），e（n-1）（az+b）+na都不为常数，由引理1 知，eac=1。

故

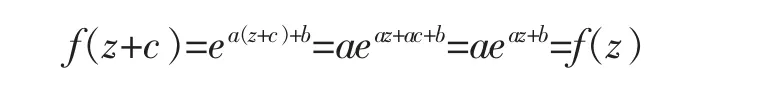
即f（z）是以c 为周期的周期函数。

定理3 得证。

4 定理4 的证明

由于d 是f（z）的一个非零Picard 例外值，且f（z）是有穷级超越整函数，因此存在多项式p（z），使得f（z）=ep（z）+d 且T（r，p（z））=S（r，f）。

因为f′（z）-afn（z）是周期函数，且周期为c，则

故ac=0。 f（z+c）=ea（z+c）+b+d＝eaz+ac+b+d=eaz+b+d＝f（z）。

即f（z）是以c 为周期的周期函数。

定理4 得证。

5 结语

文中主要研究的是形如Hayman 猜想形式的整函数的周期性，得到了一些相关结果，证明了超越整函数f（z）在有Picard 例外值时（包含零和非零两种情况），如果f′（z）-afn（z）（n≥2）是周期函数，则f（z）也为周期函数。 在文中的研究基础上，可开展更广泛的研究工作，可以探讨如果f（z）没有例外值，或者是更一般的形式，此结论是否成立。