Covering and illumination of convex bodies

WU Senlin， HE Chan

（School of Science，North University of China，Taiyuan 030051，China）

Abstract： After a survey of classical results on Hadwiger’s covering conjecture，a long-standing open problem from convex and discrete geometry，we introduced two approaches to attack this conjecture and their related results. The first approach is Chuanming Zong’s quantitative program，which is theoretically feasible if Hadwiger’s covering conjecture is true. The other tries to confirm this conjecture by attacking it for high-dimensional centrally symmetric convex bodies，whose feasibility depends on the affirmative answer to a problem posedby P. Soltan.

Key words： convex body；covering functional；Hadwiger’s covering conjecture；Soltan’s problem

1 Introduction

Hadwiger’s covering conjecture is a long-standing open problem from convex and discrete geometry，which has been studied by a large number of research papers，chapters of monographs （e.g.，[1-3]），and surveys （e.g.，[4-7]）. Despite of the efforts of mathematicians including K. Bezdek，V.G. Boltyanski，H. Hadwiger，M. Lassak，F.W.Levi，G.Livshyts，H.Martini，I.Papadoperakis，C.A.Rogers，O.Schramm，P.Soltan，V.Soltan，K. Tikhomirov，and Chuanming Zong，this conjecture is only completely solved in the two-dimensional situation and it is widely open even in R3. In this article，we briefly introduce this conjecture and classical known results，and mainly focus on more recent results in this direction and on two possible approaches towarding the complete solution of this conjecture.

We denote by Knthe family of nonempty compact convex subsets of Rn，and by Kmn（0≤m≤n） the set of compact convex subsets of Rnwhose affine dimension is m. Each member of Knnis called a convex body，i.e.，a convex body in Rnis a compact convex set having interior points. For each K∈Kn，we denote by affK，intK，relintK，bdK，and relbdK the affine hull，interior，relative interior，boundary，and relative boundary of K，respectively.

For two subsets A and B of Rn，and any λ∈R，we put

For each x∈Rn，we denote the set A+{x} by A+x and call it a translate of A. For each λ∈（0，1） and each point x∈Rn，the set λA+x is called a smaller homothetic copy of A.

For each K∈Kn，we put

where cardD is the cardinality of D，i.e.，c（K） is the minimum number of translates of relintK needed to cover K.Note that，the definition of c（K） here is slightly more general than that in the literature，namely，c（K） here is defined on Kninstead of Knn. Concerning the least upper bound of c（K） over Knn，there is a long standing conjecture：

Conjecture 1 （Hadwiger’s covering conjecture） For each integer n≥1 and each K∈Knn，we have

the equality holds if and only if K∈Knnis a parallelotope.

This conjecture is completely solved when n=2，see [8]，and it is widely open even when n=3. See the monographs [1-3]，and the surveys [4-7] for the history，known results，and relevant references of this conjecture.

2 The functional c（K）

2.1 Different interpretations of c（K）

A unit vector in Rnis called a direction. Suppose that K∈Kn，x∈relbdK，and u is a direction. If there exists a positive number λ such that

then we say that x is illuminated by u. Let A be a subset of relbdK and D be a set of directions. If each point in A is illuminated by at least one direction in D，then we say that A is illuminated by D. Put

The following lemma is mentioned in[9] without a detailed proof. For the reader’s convenience，we include a proof given in [10] （in Chinese）.

Lemma 1 Suppose that K∈Kn，c∈Rn，and 0≤α≤β≤γ. Then

Proof. We only consider the case when β>0. Let z be an arbitrary point in （αK+（1-α）c）∩（γK+（1-γ）c）.Then there exist two points x and y in K such that

Now we are ready to prove the following：

Proposition 1 Let K∈Kn. If relbdK≠Ø，then

Proof. Put m=c（K） and m′=c1（K）. Then there exists a set C={ci|i∈[m]} of m points such that K⊆relintK+C. For each point x∈relbdK，there exists i∈[m] such that x∈relintK+ci. Clearly，ci≠o. Thus

i.e.，x is illuminated by the direction -ci/||ci||. It follows that relbdK can be illuminated by

which implies that m′≤m. Thus c1（K）≤c（K）.

It is clear that c（K）≤c3（K）. By Lemma 2.3 in [11]，we have c2（K）≤c1（K）.

In the rest we show that c3（K）≤c2（K）. Put m=c2（K）. Then there exist a number λ∈（0，1） and a set C={ci|i∈[m]} of m points such that

By the definition of m，

which implies that

Let c0be a point in relintKC. For each i∈[m]，the ray from cipassing through c0intersects relbdK in a point yi.Then there exists a number αi∈（0，1） such that

Put

Then γ∈（0，1）. For each point x∈K，there exists a point z∈relbdK and a number η∈[0，1] such that x=ηc0+（1-η）z. Assume，without loss of generality，that z∈λK+（1-λ）c1. By Lemma 1

which shows that x∈γK+（1-γ）c1. It follows that

Hence c3（K）≤c2（K）=m，as claimed. □

Thus，for each K∈Knsatisfying relbdK≠Ø，c（K） is the minimum number of directions needed to illuminate relbdK，the minimum number of smaller homothetic copies of K needed to cover K，as well as the minimum number of smaller homothetic copies of K needed to cover relbdK.

It is shown in [12] that，when K∈Knncontains o in its interior，c（K） equals the least cardinality of a collection H of hyperplanes such that each exposed face of the polar body K*of K can be separated strictly from o by at least one hyperplane in H. Thus，Conjecture 1 has the following “dual” version （cf. [3]）：

Conjecture 2 Let K∈Knn（n≥3） and p be an arbitrary interior point of K. Then there exists a collection H of 2nhyperplanes such that each exposed face of K and p can be strictly separated by at least one hyperplane in H. Furthermore，2nhyperplanes are necessary only if K is the convex hull of n line segments having linearly independent directions which intersect at the common relative interior point p.See，e.g.，[12-15] for progresses towarding the solution of Conjecture 2.There are further interpretations of c（K），see，e.g.，[5] and [7].

2.2 Known upper bounds of c（K）

In 1955，F.W. Levi （see [8]） proved that

and c（K）=4 if and only if K is a parallelogram. He also pointed out that c（K）=n+1 whenever K∈Knnis smooth（at each boundary point of K，there exists a unique supporting hyperplane），and c（K）=2nwhen K∈Knnis a parallelotope.

M. Lassak proved that c（K）≤8 holds for each centrally symmetric K∈K33，see[16]. However，centrally symmetric three-dimensional convex bodies satisfying c（K）=8 have not been characterized.

In [17]，B.V. Dekster proved that，if K ∈K33is symmetric about a plane，then c（K）≤8. It is shown by M. Lassak （cf. [18]） that c（K）≤6 whenever K∈K33is a body of constant width （see [19] for more information about this special class of convex bodies）. However，it is conjectured that c（K）=4 holds for each three-dimensional convex body of constant width. For general three dimensional convex bodies，I. Papadoperakis proved that c（K）≤16，see [20]. Using I. Papadoperakis’ approach，A. Prymak and V. Shepelska proved that （see [21]）

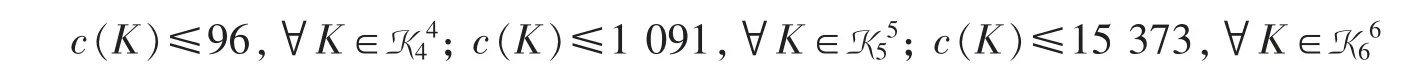
and they remarked that substantial improvements of these estimations，which are better than those provided by M. Lassak in [9]，will need new ideas. For general n≥2，C.A. Rogers and Chuanming Zong proved the following There are also many estimations of c（K） for special classes of convex bodies.

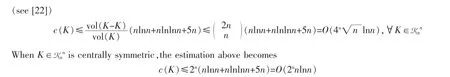
If K∈Knnis the sum of finitely many segments then K is called a zonotope；if K∈Knnis the limit（with respect to the Hausdorff metric dH（·，·），see（1） below） of a sequence of zonotopes，then K is called a zonoid.H. Martini proved that

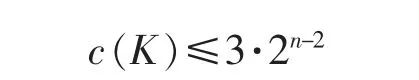
holds for each zonotope K∈Knnwhich is not a parallelotope （see [23]）. V. Boltyanski and P.S. Soltan （see [24]）obtained the same estimation for zonoids. Later，V. Boltyanski showed that this estimation is valid also for belt bodies （see [25]）.

O. Schramm [26] proved that

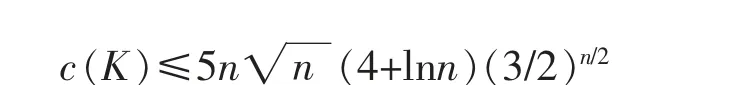
holds for each K∈Knnhaving constant width. This estimation yields c（K）≤2nfor n-dimensional bodies of constant width when n≥16.

2.3 The upper semicontinuity of c（K）

Hadwiger’s covering conjecture is hard partially because c（K） is upper semicontinuous. For two subsets L and M of Rn，the Hausdorff distance dH（L，M） between them is given by

where B2nis the unit ball of Rn. Concerning the continuity of c（K），we have the following result （see，e.g.，Theorem 34.9 of [1]）：

Theorem 1 （Upper semicontinuity） For each K1∈Knn，there exists a positive δ=δK1such that

Therefore，verifying Hadwiger’s covering conjecture for a dense subset of the metric space（Knn，dH（·，·））does not provide a complete solution. In fact，we already know that c（K）=n+1 for each K∈Knnwith smooth boundary，and this class of convex bodies are dense in （Knn，dH（·，·））.

3 Covering functionals and Zong’s quantitative program

Since c（K） is an affine invariant，it is more natural to measusre the difference between two convex bodies using the Banach-Mazur metric. For two convex bodies K1and K2，put

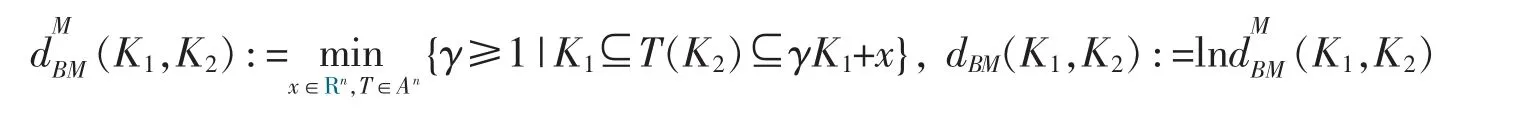
where Anis the set of all non-sigular affine transformations on Rn. The number dBM（K1，K2） is called the Banach-Mazur distance between K1and K2. It is clear that dBM（K1，K2）=0 if and only if K1and K2are affinely equivalent.Denote by ～ the affine equivalence，and by[K] the equivalence class of K∈Knn. For each pair of convex bodies K1and K2，put

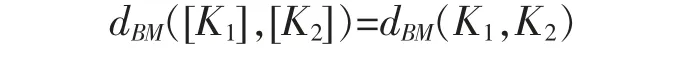
Then （Knn/～，dBM） is a compact metric space.

Using dBM（·，·），G. Livshyts and K. Tikhomirov proved that，for each K[0，1]nthat is sufficiently close to[0，1]nin dBM（·，·），we have c（K）≤2n-1（see [27]）.

For each K∈Knnand each m∈N，we put

and Γm（[K]）=Γm（K）. Since c（K） equals the the least number of smaller homothetic copies of K needed to cover K，c（K）≤m if and only if Γm（K）<1. Concerning the continuity of Γm（·），Chuanming Zong proved the following：

Theorem 2（[28]） For each ε>0，and each pair of convex bodies K，L∈Knnsatisfying dBM（K，L）≤ln（1+ε），we have

Hence Γm（·） is uniformly continuous on （Knn/～，dBM）. K. Bezdek and M.A. Khan proved that Γm（·） is Lipschitz continuous. More precisely，they showed that （see [29]）

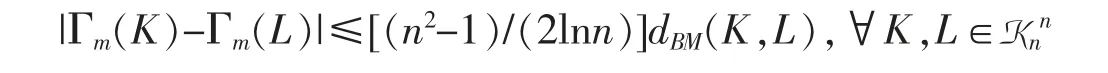
Now it is clear that

Based on these observations，Chuanming Zong proposed the following program to attack Hadwiger’s covering conjecture.

（ⅰ）Get a good guess c^nof cnby estimating Γ2n（K） for special classes of convex bodies.

（ⅱ）Choose a suitable ε>0 and construct an ε-net N of Knn.

（ⅲ）For each K∈N verify that Γ2n（K）≤c^n.

As pointed out in [7]，this is the first attempt at a computer-based resolution of Hadwiger’s covering conjecture. It is feasible if （2） holds true，and it is more promising for lower dimensional situations.

We note that，after proving （2），we still need to characterize n-dimensional convex bodies satisfying c（K）=2n.

Known estimations of Γm（·）.

Although there is still no characterization of convex bodies in Knnsatisfying c（K）=2n，Chan He et al. proved the following result concerning the greatest lower bound for Γ2n（K） （see [30]）

and “=” holds if and only if K～[0，1]n.

For the Euclidean disc B22，triangle Δ，tetrahedron T，cross-polytope B13，and the Euclidean ball B23，precise values of Γm（·） for paricular choices of m are known，see Table 1.

Table 1 Known precise values of Γm（·）

For each pair of positive integers m and n，put

When n=2，the precise values of Γ－（n，m） and Γ+（n，m） are known for some particular m. See Table 2.

Table 2 Known values of Γ-（2，m） and Γ+（2，m）

In particular，M. Lassak proved that Γ7（K）=1/2 holds for each centrally symmetric K∈K22（cf. [31]）.

When n≥3，estimating Γm（K）is more difficult.This situation can be seen from the following estimation(cf.[32])

One can also use the knowledge of covering functionals for lower dimensional convex bodies to estimate Γm（K） for higher dimensional convex bodies. In this direction，Donghai Ji et al. observed that，if K∈Knnand C=K×[-1，1]，then

Note that the estimation （3） is not always best possible. Characterizing the situation when the inequality in（3） becomes equality is still open and interesting.

If K∈Knnis symmetric about the origin o，then （Rn，||·||K） is a Banach space having K as the unit ball，where

is the gauge or the Minkowski functional of K. Let ε∈[0，2]，u∈bdK. The number

is called the directional modulus of convexity. For each u∈bdK and each number λ>0，put

Since λ（P） plays an important role in the estimation above，the authors proved the following properties for λ（P）.

（ⅰ）If dimP≥1，then λ（P）≤1/2.

（ⅱ）If P∈Knn，then λ（P）≥1/（n+1）；the equality holds if and only P is a simplex.

（ⅲ）If P is centrally symmetric and planar，then λ（P）=1/2.

（ⅳ）If P is centrally symmetric，then λ（P）=min{λ（F）|F is a facet of P}.

（ⅴ）If P is three-dimensional，centrally symmetric，and each facet of P is also centrally symmetric，then λ（P）=1/2.

4 Another possible approach

In this section，we present another possible approach to attack Conjecture 1 and related results. The authors learnt from H. Martini the following problem posed by P. Soltan.

Problem 1 Suppose that T=-B∈Knnand K=conv（（T×{1}）∪（B×{0}））. Is it true that c(K)=c(T)+c(B)=2c(T)?

then K∈K33is a cube and c（K）=c（T）+c（B）. Senlin Wu and Ying Zhou showed that （cf. [11]）：

（ⅰ）c（K）≤c（T）+c（B）；

（ⅱ）if T is a translate of B，then c（K）=c（T）+c（B）=2c（T）；

（ⅲ）if T+c⊆relintB holds for some point c∈Rn-1，then c（K）=1+c（B）；

In particular，they solved Conjecture 1 for three-dimensional convex bodies constructed by （5）.