完整系统的分数维梯度表示及其稳定性分析
王嘉航, 顾 玲, 翟相华
(1.苏州科技大学 土木工程学院,江苏 苏州 215011;2.河海大学 土木与交通学院,江苏 南京 210098)
梯度系统是一类数学系统,是微分方程和动力系统中的重要部分。 如果一个力学系统能够成为梯度系统,那么就可以利用梯度系统的性质来研究力学系统的行为,特别是稳定性问题[1]。 约束力学系统的梯度表示及其稳定性分析研究已经取得了一定的重要成果[2-11],但这些研究成果大多是针对整数阶模型的。 在实际应用中,相比整数阶模型而言,分数阶模型往往更为合适,如在粘弹性流体力学、量子力学、统计力学、砂岩力学等性质研究时往往需要用到分数阶微分方程[12]。 近年来,分数维研究逐渐成为了物理、力学以及数学等领域的热点研究问题。文献[13]指出任意阶α≠1(包括α 为整数)的分数维梯度系统都可称之为分数维的。关于Birkhoff 系统、非自治Birkhoff 系统、弱非完整系统以及完整系统的分数维梯度表示已有相关研究结果[14-18]。笔者进一步研究准坐标下完整系统、相对运动动力学系统和变质量完整系统这三类系统的二阶分数维梯度表示,并利用分数维梯度系统的性质研究系统的稳定性问题,最后举例说明结果的应用。
1 准坐标下完整系统的分数维梯度表示及其稳定性分析
1.1 系统的运动微分方程
系统的运动微分方程可以表示为[2]

其中L*为用准速度表示的Lagrange 函数,有

对准坐标πs的偏导数定义为

其中Ps*为用准速度表示的非势广义力,有

设系统非奇异,即

则可由方程(1)解出所有的ω˙s,简单记作

1.2 系统的分数维梯度表示及其稳定性分析
设准坐标下完整系统不含时间t,若将方程(6)化为梯度系统,需要将其表示为一阶形式,令

则方程(6)可统一表示为

其中

对于式(8),如若满足以下条件
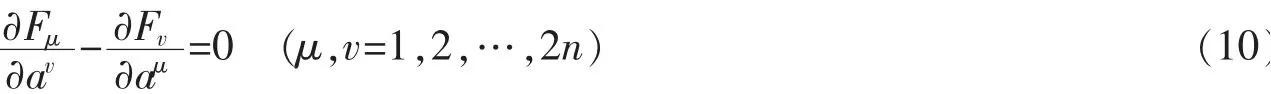
则它是一个梯度系统,此时可求得势函数V=V(a),使得

应注意,如果条件(10)不满足,还不能断定它不是一个梯度系统,因为这依赖于方程组的一阶表达形式[1]。
一般情况方程(8)不是一个α=2 阶的分数维梯度系统,若满足则是一个α=2 阶的分数维梯度系统。
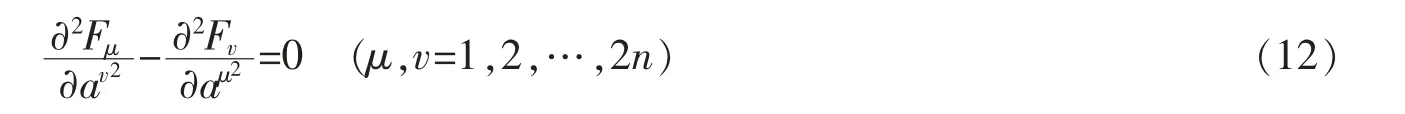
满足条件(12)的分数维梯度系统,可以求得势函数V=V(a),使得

如果势函数V 在解的邻域内正定,那么势函数V 可取为Lyapunov 函数,利用Lyapunov 定理来研究解的稳定性,也可利用Rumyatsev 定理来研究系统部分变量的稳定性。如果势函数V 不能成为Lyapunov 函数,那么根据分数维梯度系统任一平衡点处的线性化系统都只有实特征值这一性质,可通过求解其线性化系统的特征根来分析解的稳定性:如若特征根全为负实根,则解是渐近稳定的;如果特征根存在正实根,则解是不稳定的。
1.3 举例
二自由度系统为

试将其化为α=2 阶的分数维梯度系统,并研究零解的稳定性。
解 由系统的运动微分方程(1)得
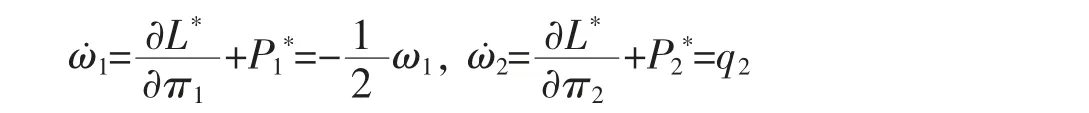
令,a1=q1, a2=q2, a3=-ω1, a4=-ω2。
由方程(8)得

因为

所以条件(10)不满足,此系统不是一个通常梯度系统。 但满足条件(12),所以该系统是α=2 阶的分数维梯度系统。
由式(13)可以求出势函数V 为

势函数V 在a1=a2=a3=a4=0 的邻域内正定,由Lyapunov 定理可知:零解a1=a2=a3=a4=0 是稳定的。
2 相对运动动力学系统的分数维梯度表示及其稳定性分析
2.1 系统的运动微分方程
系统的运动微分方程有形式[2]

2.2 系统的分数维梯度表示及其稳定性分析


势函数在a1=a2=0 的邻域内正定,根据Lyapunov 定理可知:零解a1=a2=0 是稳定的。
3 变质量力学系统的分数维梯度表示及其稳定性分析
3.1 系统的运动微分方程
系统的运动微分方程有形式[2]

设系统(28)非奇异,即设

则可由方程(28)解出所有广义加速度,记作

令

则方程(31)可写为

其中

引进广义动量ps和Hamilton 函数H

则方程(28)可以写为
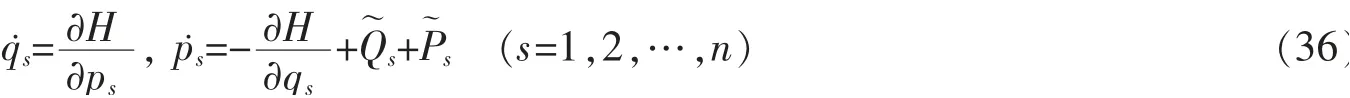
其中

方程(36)还可写成如下的形式

其中

3.2 系统的分数维梯度表示及其稳定性分析
一般来说,系统(33)或者(38)都不是梯度系统,对于方程(33),如果满足条件

则是一个α=2 阶的分数维梯度系统。 对于方程(38),如果满足条件
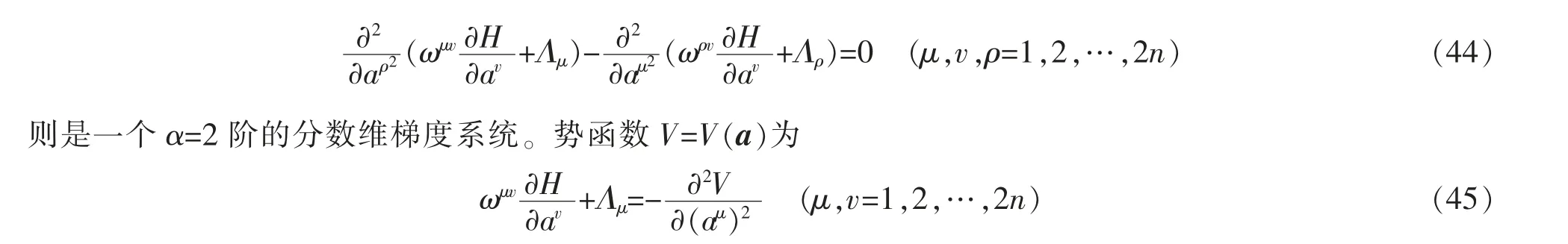
方程(33)或者方程(38)在条件(43)或条件(44)下,可以化成阶α=2 的分数维梯度系统,如果势函数V在解的邻域内正定,可以利用Lyapunov 定理来研究解的稳定性,也可利用Rumyatsev 定理来研究系统部分变量的稳定性。
3.3 举例
一变质量质点以水平角β 的初速度v0射出后,在重力场中运动,其质量变化规律为m=m0exp(-γt),其中m0,γ 为常数,假设微粒分离的相对速度vr的大小为常量,方向永远与v0相反。 试将系统的运动微分方程化为α=2 阶的分数维梯度系统,并且研究其零解的稳定性。
解 系统的Lagrange 函数和反推力分别为

其中,q1=x,q2=y 分别为水平坐标和铅垂坐标,广义力为

4 结语
研究了准坐标下完整系统、相对运动动力学系统和变质量完整力学系统这三类系统成为α=2 阶的分数维梯度系统的条件,并给出势函数V。 若势函数V 可以取为Lyapunov 函数,则可以利用Lyapunov 定理来研究解的稳定性,也可利用Rumyatsev 定理来研究系统部分变量的稳定性;如果势函数V 不能成为Lyapunov函数,则可以根据其线性化系统的特征根的正负来判断解的稳定性。 例题说明了方法的有效性。
- 苏州科技大学学报(自然科学版)的其它文章
- 关于整函数的周期性研究
- 拓展的灰色GM(1,1)模型及其应用
- 关于高阶线性复微分方程整函数解的Borel 方向
- Several theorems of Helly type for spherically convex sets
- Doping of strontium in MoS2 widened d-spacing of plane (101)and piezo-enhanced photocatalytic evolution of hydrogen from ammonia borane upon near-infrared irradiation
- Covering and illumination of convex bodies

