基于CEEMDAN 法的隧道爆破信号趋势项去除❋

张 佳 赵 岩

①山西工程科技职业大学(山西太原，030031)

②中国矿业大学(北京)力学与建筑工程学院(北京，100083)

引言

爆破施工由于经济效益好、回报率高、操作易行等优点已被广泛应用于隧道掘进、矿山开采、坝体修建等大型土建工程中[1-3]。 然而，爆破施工带来的飞石、有害气体及爆破振动等附加产物均会对人体及周边环境造成不利影响。 其中，隧道爆破施工引起的振动效应极易危害建(构)筑物的正常运营及结构安全。

爆破振动信号分析是研究爆破振动效应的主要途径[4-5]。 爆破振动信号采集过程中，受采样环境及测试仪器的影响，采集到的信号往往会出现时程波形偏离中心基线的现象，即产生趋势项[6]。 受趋势项的影响，实测信号的时域分析及频谱分析准确性下降，甚至会出现低频信号失真的现象。 因此，有必要在信号分析前对爆破振动信号进行趋势项的消除处理。

目前，信号趋势项消除的方法主要包括最小二乘拟合法[7]、小波法[8]、EMD(empirical mode decomposition)法[9]、EEMD(ensemble empirical mode decomposition)法[10]、VMD(变分模态分解，variational mode decomposition)法[11]等。

最小二乘法通过多项式拟合逼近原始信号，去除信号中的趋势部分，但其去除效果与多项式函数的阶次选择有关，受主观影响较大。 小波法适用于非稳态信号的处理，但选取不同小波基函数、不同分解深度可能会得到不同的结果。 因此，以上两种方法均要求研究人员具有一定的经验。

EMD 法根据信号特征可以将原始信号分解为一系列频率由高到低排列的本征模态分量，不需要过多的经验就可以识别信号趋势项，具有自适应性；但EMD 过程中存在端点效应及模态混叠等问题，影响识别效果。 为了解决EMD 法存在的问题，EEMD法、CEEMD (complementary ensemble empirical mode decomposition)法[12]、VMD 法、PEMD[13](PCA 联合EMD)法等改进方法被应用于信号预处理中。 EEMD 法与CEEMD 法以EMD 法为基础，在信号中加入高斯白噪声来抑制模态混叠；但受算法本身限制，分解过程中常常会残留白噪声，影响分解效果。VMD 法通过迭代搜寻变分模型最优解，自适应地实现信号的频域剖分，可有效识别低频信号；但VMD法分解效果受信号频率及振幅的影响较大，只有在特定频率、振幅范围内才能得到满意效果。 PEMD法在EMD 法中引入主成分分析，得到多个完全正交的模态分量，解决了模态混叠的问题；然而，PEMD法只重构了累计贡献率超过85%的主成分[13]，并未真正对信号趋势项进行识别。

为解决上述问题， 引入一种基于 CEEMDAN[14-16]法的趋势项去除方法。 CEEMDAN 法以EEMD 法、CEEMD 法为基础，很好地解决了分解残留白噪声的问题；同时，相比于VMD 法、PEMD 法、自适应连续波法等，CEEMDAN 法不受信号自身条件限制，具有较强的自适应性，可提高识别精度。

1 CEEMDAN 趋势项去除

1.1 CEEMDAN 原理

EEMD 法及CEEMD 法解决了EMD 法存在的模态混叠问题，但分解过程中并不能完全消除添加的噪声信息，从而影响信号趋势项的消除效果。CEEMDAN 法[17-19]法从两方面解决了分解存在的问题:1)每一次分解完成后加入成对正负高斯白噪声；2)每分解得到一阶本征模态分量，随即进行1次平均计算，直至整个分解过程结束。 如此操作，可以在EEMD 法及CEEMD 法的基础上解决白噪声的残留问题。

1.2 趋势项判别方法

采用均值比法[20]识别CEEMDAN 法分解得到的本征模态分量u及余项R，判断哪些分量包含信号趋势项。

1)求得原始信号、模态分量u以及余项R的均值为:

式中:n表示信号长度；ul为第l个模态分量(l＝1，2，…，L)。

2)计算得到每个模态分量及余项与原始信号的均值比:

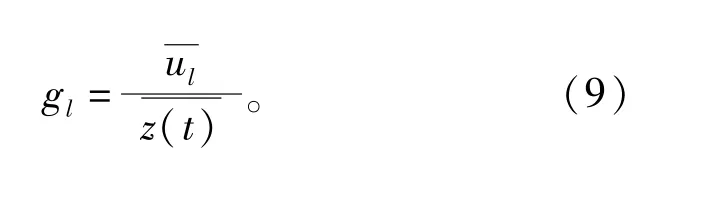
3)从余项开始，反向累加余项及各个模态分量的均值比G，直至G ＞0.95:

4)当G≥0.95 时，停止计算，认为第L列至第P列余项及模态分量之和为信号趋势项。

2 仿真计算

为了验证引入的CEEMD 法趋势项消除方法的可行性及普适性，首先利用正弦信号v(t) ＝(1 ＋0.5sin0.5π)sin165πt添加人为趋势项，从而进行仿真计算。

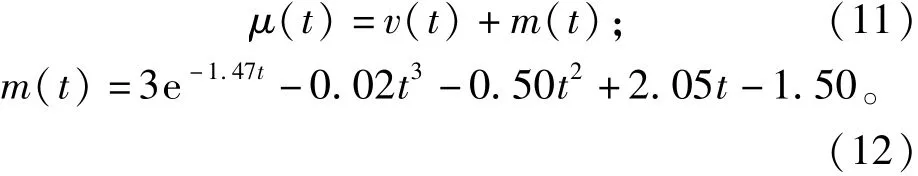
式中:v(t)为无趋势项信号；m(t)为人为添加的趋势项；μ(t)为添加趋势项的混合信号。

为模拟真实监测环境中复杂的监测条件，人为添加的趋势项包含线性、多项式及指数型3 种趋势项模式[21]。

人为添加趋势项如图1 所示；添加趋势项前、后的仿真信号见图2。

图1 趋势项时程曲线Fig.1 Time history curve of the trend item

图2 初始信号及混合信号的时程曲线Fig.2 Time history curves of initial signals and mixed signals

利用CEEMDAN 法将混合信号μ(t)分解为13个本征模态分量及一个余项，并计算模态分量及余项与初始信号的均值比，计算结果见表1。

从表1 可知，余项R与u13的均值比累加值超过0.95。 根据均值比法，可以认为R与u13的重构信号为信号的趋势项。

表1 模态分量及余项与初始信号的均值比Tab.1 Mean ratio of the modal components and the residual term to the initial signal

作为对比，分别应用EMD 法及EEMD 法识别信号趋势项，并将EMD 法、EEMD 法、CEEMDAN 法识别筛选出的信号趋势项与人为添加的趋势项绘制于图3。

图3 不同方法识别的仿真信号中的趋势项对比Fig.3 Comparison of trend items in simulation signals identified by different methods

由图3 可知，EMD 法、EEMD 法、CEEMDAN 法3 种方法均可以从仿真信号中提取趋势项，但不同分解方法会得到不同的识别结果。 其中，CEEMDAN 法提取结果更接近人为添加的趋势项。

为了进一步验证CEEMDAN 法分解在识别信号方面的优势，分别计算3 种方法提取出的趋势项与人为添加趋势项m(t)的平均误差、最大误差及均方根差，计算结果见表2。

表2 不同识别方法的统计性参数Tab.2 Statistical parameters of different identification methods

由表2 可知: 与EMD 法相比，CEEMDAN 法提取结果的平均误差、最大误差及均方根差分别下降79.69%、61.62%、42.76%；与EEMD 法提取结果相比，CEEMDAN 法的平均误差、最大误差及均方根差分别下降80.67%、70.30%、42.76%。 因此，证明CEEMDAN 法识别筛选出的趋势项与原添加趋势项相似度最高。

综上所述，CEEMDAN 法在数值仿真领域应用效果良好，为后续实测爆破信号中的应用奠定了一定的理论基础。

3 实例分析

以京张高铁某隧道爆破工程为例，研究CEEMDAN 法在实测爆破信号趋势项识别中的应用。 隧道位于河北省张家口市宣化区陈家庄附近，穿越草帽山主山脉。 隧道围岩主要为全风化凝灰岩。 凝灰岩具有中等膨胀性，遇水力学性质会出现明显劣化，给隧道爆破施工带来了困难。 图4 为隧道进口施工场地布置图[22]。

图4 隧道场地布置Fig.4 Site layout of the tunnel

利用TC-4850爆破测振仪采集现场爆破振动信号，采样频率为5 000 Hz，测振仪最小工作频率为5 Hz，可以通过配套的处理软件对实测信号进行分析。 具体测点布置见图5[23]。 典型爆破信号时程曲线及功率谱密度如图6、图7 所示。

图5 测点布置Fig.5 Layout of measuring points

图6 典型爆破振动信号的时程曲线Fig.6 Time history curve of typical blasting vibration signal

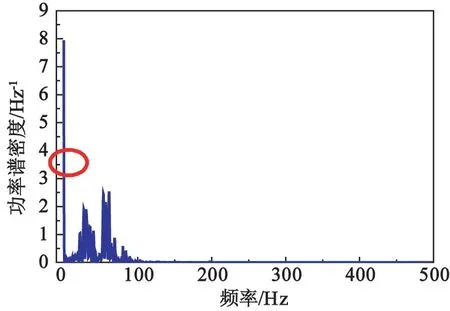
图7 典型爆破振动信号的功率谱密度Fig.7 Power spectrum of typical blasting vibration signal

由图6 可知，受监测环境及低频振动的影响，爆破振动信号在起点处表现出明显的零点漂移。 从图7 信号功率谱密度可以看出，在0 ～5 Hz 范围内，爆破信号存在明显的低频超高异常幅值，严重影响了信号分析的准确性。 因此，有必要在信号分析前对实测信号进行趋势项消除处理。

首先，利用CEEMDAN 法将实测信号分解为15个本征模态分量及1 个余项，具体波形如图8 所示。计算各个模态分量及余项的均值比，结果见表3。

图8 本征模态分量及余项的波形Fig.8 Waveform of eigenmode components and the residual term

表3 各模态分量及余项与原始信号均值比Tab.3 Mean ratio of each modal component and the residual term to the original signal

由表3可知，余项R与模态分量u15的均值比累加值超过0.95，根据均值比识别准则，余项R与模态分量u15可以视为信号趋势项有效组成部分。 因此，在原始信号的基础上去除R与u15分量，得到消除趋势项的修正信号及功率谱密度曲线如图9 所示。

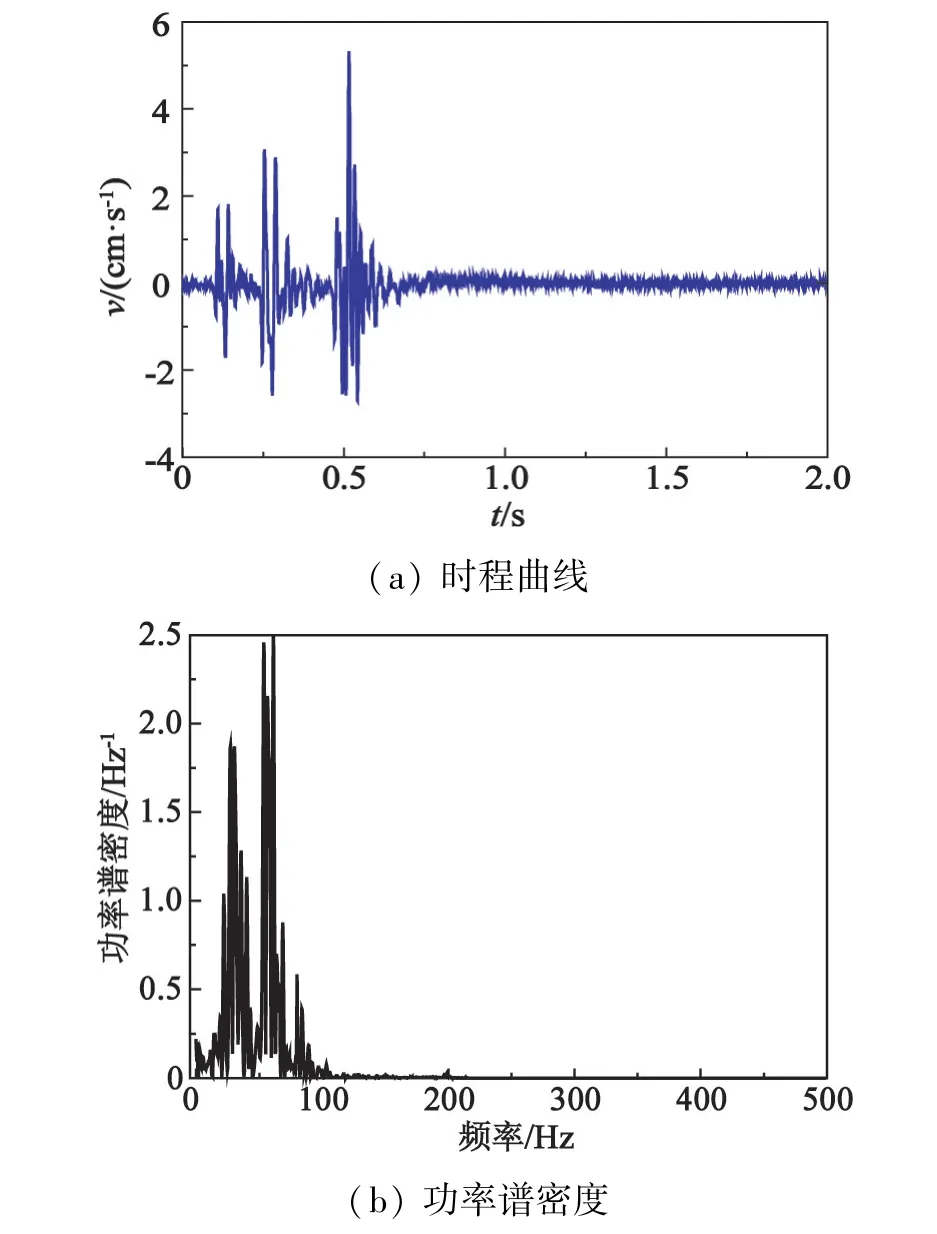
图9 去趋势项后振动信号的时程曲线及功率谱密度Fig.9 Time history curve and power spectral density of blasting vibration signal after the removal of trend item

对比图6 与图9(a)可以发现，经CEEMDAN 法去趋势项处理后，基本消除了爆破信号中的零点漂移现象，信号的基线偏离问题得到了解决。 此外，由图9(b)可知，经预处理后的爆破振动信号功率谱密度消除了原始信号频谱中的超高幅异常低频分量，修正信号的主频集中在62 Hz 附近，满足爆破信号主频率的分布范围[24-25]。

4 结论

以京张高铁某隧道为工程背景，引入一种基于CEEMDAN 法消除隧道爆破信号趋势项的方法，并通过数值仿真验证了其普适性。

1) CEEMDAN 法通过优化算法消除了EEMD法及CEEMD 法中存在的残留白噪声，可以应用于爆破振动信号的趋势项识别。

2) 数值仿真结果显示:CEEMDAN 法可以有效地去除仿真信号中添加的人为趋势项；与EMD 法及EEMD 法相比，CEEMDAN 法识别趋势项的精度更高，CEEMDAN 法筛选出的结果与人为添加的趋势项具有更好的相关性。

3) CEEMDAN 法可以有效地去除原始爆破实测信号中的趋势项，经CEEMDAN 法处理后的修正信号解决了爆破振动信号零点漂移及基线偏离问题。 依据信号功率谱密度，原始信号的超高异常低频分量被去除，信号主频回归到爆破振动信号主频率分布范围，为后续爆破振动信号的准确分析奠定了基础。