镜像铣削加工奇异区域刀具路径优化

章绍昆，毕庆贞，王宇晗

上海交通大学 机械与动力工程学院，上海 200240

航空航天领域广泛采用重量轻、结构强度高的大型薄壁件作为飞行器外表零件，如飞机蒙皮、火箭燃料贮箱等。大型薄壁件尺寸大、厚度薄、刚性弱，材料去除量大，加工过程易发生振动和变形[1]。传统的化铣方法由于精度低、污染高，已无法满足新型飞机蒙皮等大型薄壁件的制造质量要求[2]。镜像铣削是一种针对大型薄壁件开发的新型加工技术[3]。镜像铣削系统配备两个镜像对置的五轴机床，分别为铣削头和支撑头，如图1所示。其中铣削头搭载主轴系统，加工时完成材料去除功能；而支撑头与铣削头镜像对称，加工时从背部为薄壁件提供局部支撑，提高加工区域刚性，抑制振动减小变形[4]。同时，支撑头上可以集成传感器，在线测量零件变形、剩余壁厚等信息，使得加工误差实时补偿成为可能。与化铣相比，镜像铣削降低了加工成本，提高了加工效率和精度，是大型薄壁件加工技术的发展趋势。

图1 镜像铣削系统原理Fig.1 Principle of mirror milling system

由于铣削头和支撑头均为五轴机床，在加工时不可避免地存在五轴运动奇异点问题[5]。在奇异点附近机床动态性能急剧下降，一方面直接影响机床的运动精度，另一方面机床减速严重，造成切削力突变，两者均影响大型薄壁件的壁厚精度和表面质量，降低加工效率。

现有的五轴加工奇异点避免方法主要针对刀路规划、后置处理和实际加工3个阶段展开。在刀路规划阶段，可以通过优化刀轴矢量来避开奇异区域。Affouard[6]、Yang[7]和Wan[8]等将各刀位点的刀轴矢量拟合为样条曲线，通过对样条曲线控制点进行微调，保证刀轴矢量避开五轴机床奇异区域，提高刀轴矢量的光顺性。Castagenetti[9]和Lin[10-11]等定义了刀轴矢量的可行域，在可行域内实现刀轴矢量的优化，进而避开奇异区域，以获得更好的加工质量。王浏宁[12]通过监测刀轴矢量与旋转轴的夹角，对处于奇异区域的刀位点进行优化。Tajima和Sencer[13]通过实时路径规划避开奇异区域。Lartigue[14]和Lu[15]等针对侧铣加工，通过调整刀路控制点来修改刀路，提高了奇异点附近旋转轴的光顺性，保证了加工精度。周金强[16]和李冬冬[17]等通过刀位点插值降低了S试件加工奇异区域的非线性误差。在刀路规划阶段可以根据工件模型信息，有效地控制由刀轴方向改变引起的加工误差，在避开奇异点的同时保证加工精度，因此应用较为广泛。在后置处理阶段，Sørby[18]对非正交机床进行运动学建模，进而在后置处理中对奇异点附近的旋转轴运动量进行微调，以提高刀路在奇异区域的鲁棒性。值得注意的是，这类方法在调整旋转轴运动量时不可避免地会引入加工误差。Munlin等[19]在后置处理中通过最短路径规划来降低奇异点附近的运动误差。王丹等[20]通过线性插值来提高奇异区域的加工精度。在实际加工阶段，Cripps[21]和王瑞秋[22]等详细地分析了奇异点存在的原因及其影响，提出了将工件倾斜装夹来避开奇异点，该方法受限于工件和刀路的实际形状。Anotaipaiboon等[23]通过优化机床结构来避免加工奇异点。

综上所述，现有方法主要通过修改刀轴矢量来实现奇异区域内的刀具路径优化。但对于镜像铣削而言，为了保证壁厚实时测量的准确性和稳定性，刀轴矢量必须垂直于工件表面[24]，而直接修改刀轴矢量的方法会使得刀轴矢量偏离工件法向，影响壁厚测量的准确性和稳定性，无法满足镜像铣削的加工要求。

针对镜像铣削过程中存在的奇异点问题，首先，利用机床旋转轴运动学变换模型分别推导铣削头和支撑头旋转轴微分运动关系，分析奇异点存在的原因，定义奇异区域范围。然后，提出镜像铣削加工刀路约束条件和刀路光顺性度量方法，建立刀路优化模型。将刀路映射到参数域内并拟合为样条曲线，对于穿过奇异区域的刀路通过优化模型对参数域内的刀路曲线进行微调，使得优化后的刀路更加光顺，以提高加工精度和表面质量，减少奇异区域内的加工时间。最后通过镜像铣削加工实验验证本文所提方法有效性。

1 镜像铣削系统运动学变换与奇异点分析

以图2所示的镜像铣削实验平台为研究对象。其中，铣削头为AC双摆头结构机床，其旋转轴标记为A1轴和C1轴，行程分别为[-90°,90°]和[-360°,360°]；支撑头为AB双摆头结构机床，其旋转轴标记为A2轴和B2轴，行程分别为[-65°,65°] 和[-65°,65°]。

图2 镜像铣削实验平台Fig.2 Experiment platform for mirror milling

从旋转轴运动学变换模型及其微分运动关系出发，分别分析了铣削头和支撑头的奇异点和奇异区域范围及其影响。

1.1 铣削头运动学变换与奇异点分析

铣削头为AC双摆头结构机床，其运动学变换模型和微分运动关系的推导过程在文献[25]中有详细的叙述，为便于读者理解，做简要描述。铣削头旋转轴运动学模型的表达式为

(1)

式中：[i,j,k]T为五轴铣削刀路刀轴矢量；A1和C1为机床A1轴和C1轴的旋转量。

根据旋转轴运动学模型可以得到其逆变换为

(2)

式中：atan2(y,x)为点(x,y)的方位角，定义为

atan2(y,x)=

可以看到，对于同一刀轴矢量[i,j,k]，旋转轴在A1∈[-90°,90°]和C1∈[-180°,180°]行程范围内总存在两组对应的基础解(A1,1,C1,1)和(A1,2,C1,2)，且A1,1+A1,2=0°，C1,1-C1,2=±180°。其中，k决定了A1轴的旋转量，而IJ平面中点(i,j)的方位角决定了C1轴的旋转量。鉴于所用镜像铣削系统C1轴行程为[-360°,360°]，相比基础解所在区间多了一个周期，因此C1轴相应地多了2组解，共存在4组解。

对式(1)求偏微分，得到铣削头旋转轴微分运动关系为

(3)

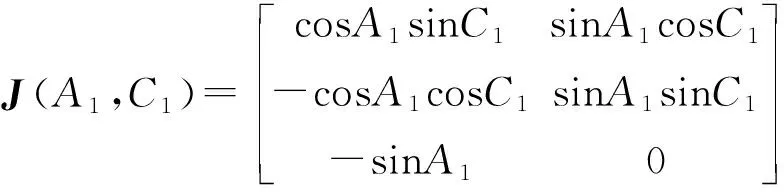
当A1=0时，J(A1,C1)为非列满秩矩阵，无论C1轴旋转量为多少，刀轴方向始终不会改变，即机床在此处损失了一个旋转轴的运动能力[25]。此时机床旋转轴处于奇异状态，对应的刀轴矢量[i,j,k]T=[0,0,1]T为铣削头的奇异点。

当A1≠0时，从旋转轴微分运动关系可以得

(4)

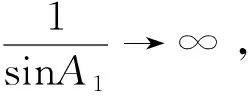
当A1轴位于奇异区域内时，一方面，机床动力学性能难以满足旋转轴角度的剧烈变化，机床减速严重，造成切削力的波动，影响加工精度，且降低加工效率；另一方面，由于机床旋转轴运动与刀尖点运动存在非线性关系[25]，在短距离内旋转轴迅速转动，造成刀尖点运动的非线性误差，直接影响加工精度和表面质量。

1.2 支撑头运动学变换与奇异点分析

支撑头的A2轴和B2轴旋转量分别记为A2和B2。利用文献[26]建立的支撑头运动学变换矩阵，可以得到支撑头旋转轴运动学模型为

(5)

将式(5)对A2和B2求偏微分，可以得到支撑头旋转轴微分运动关系为

(6)

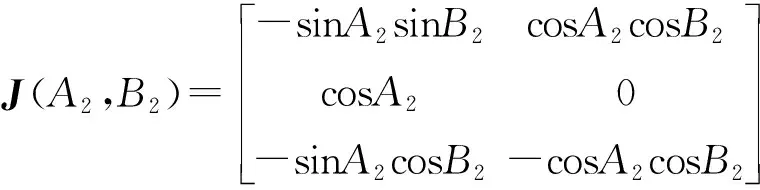
当A2=±-90°时，J(A2,B2)为非列满秩矩阵，对应的刀轴矢量[i,j,k]T=[0,±1,0]T为支撑头的奇异点。考虑到支撑头A2轴的行程为[-65°，65°]，离支撑头奇异点较远，因此在镜像铣削加工中可以不必考虑支撑头的奇异点问题。

从上述分析可以看出，在镜像铣削系统的旋转轴行程范围内，仅铣削头存在奇异点，而支撑头无奇异点。因此，刀具路径优化方法仅考虑铣削头的奇异区域。

2 镜像铣削奇异区域内的刀具路径优化

2.1 镜像铣削加工刀具路径规划约束条件

在镜像铣削过程中，支撑头与铣削头镜像同步运动，并通过集成在支撑头轴线上的超声波测厚传感器实时测量当前加工位置的剩余壁厚，进而实现壁厚闭环控制。为了保证厚度测量的准确性，支撑头轴线应时刻与工件表面法向一致，即

V=nS

(7)

式中：V=[i,j,k]T为当前刀位点处的刀轴矢量；nS为加工曲面S在当前刀位点处的法向。

为了保证传感器测量的厚度为当前刀位点铣削后的剩余壁厚，还需要保证镜像铣削刀路在当前刀位点的有效切宽可以完全覆盖支撑头轴线，即刀路切宽大于刀具底刃半径:

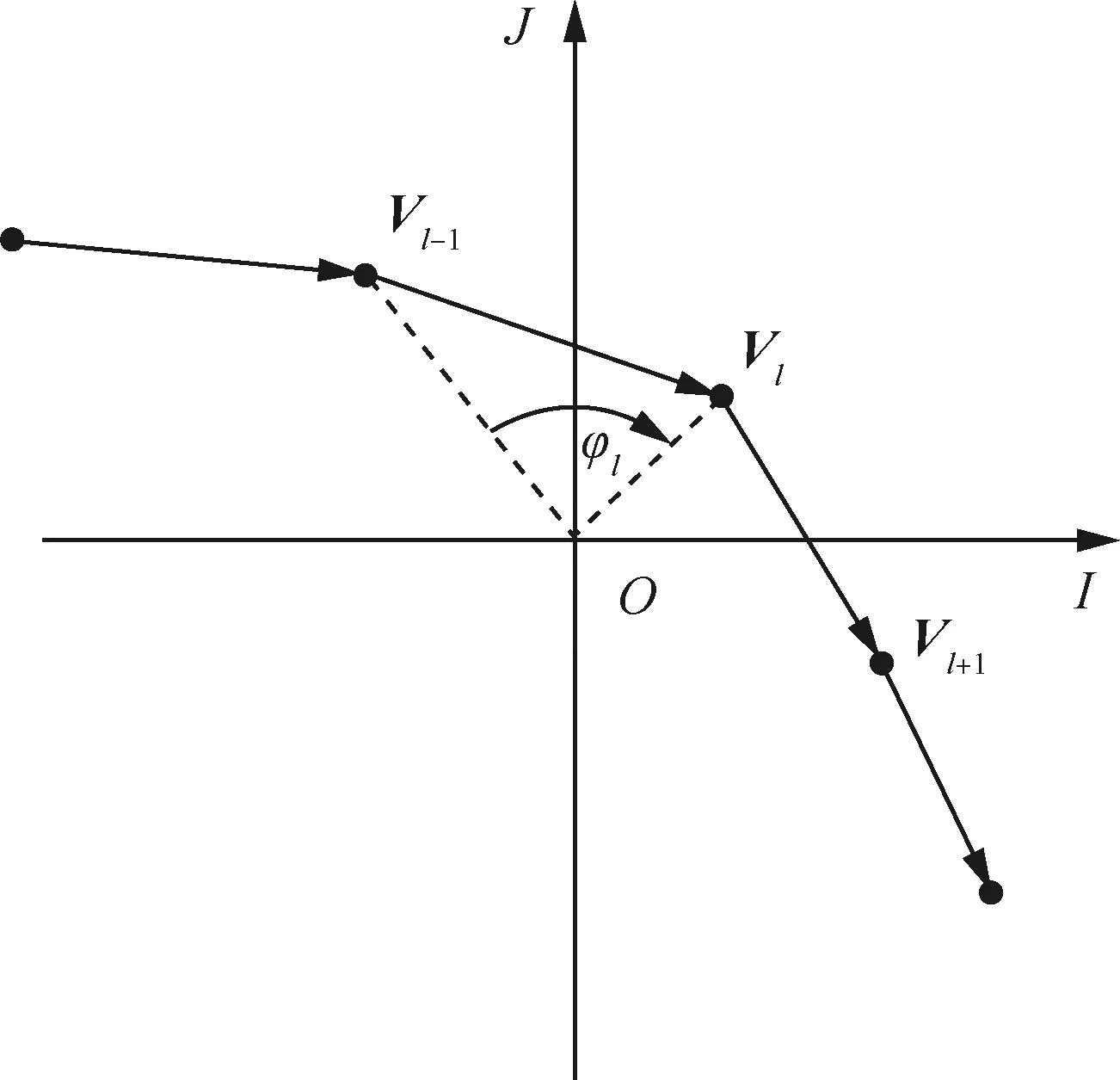
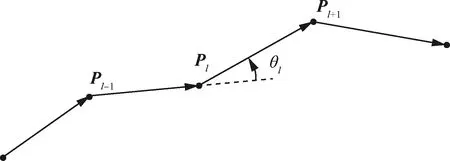
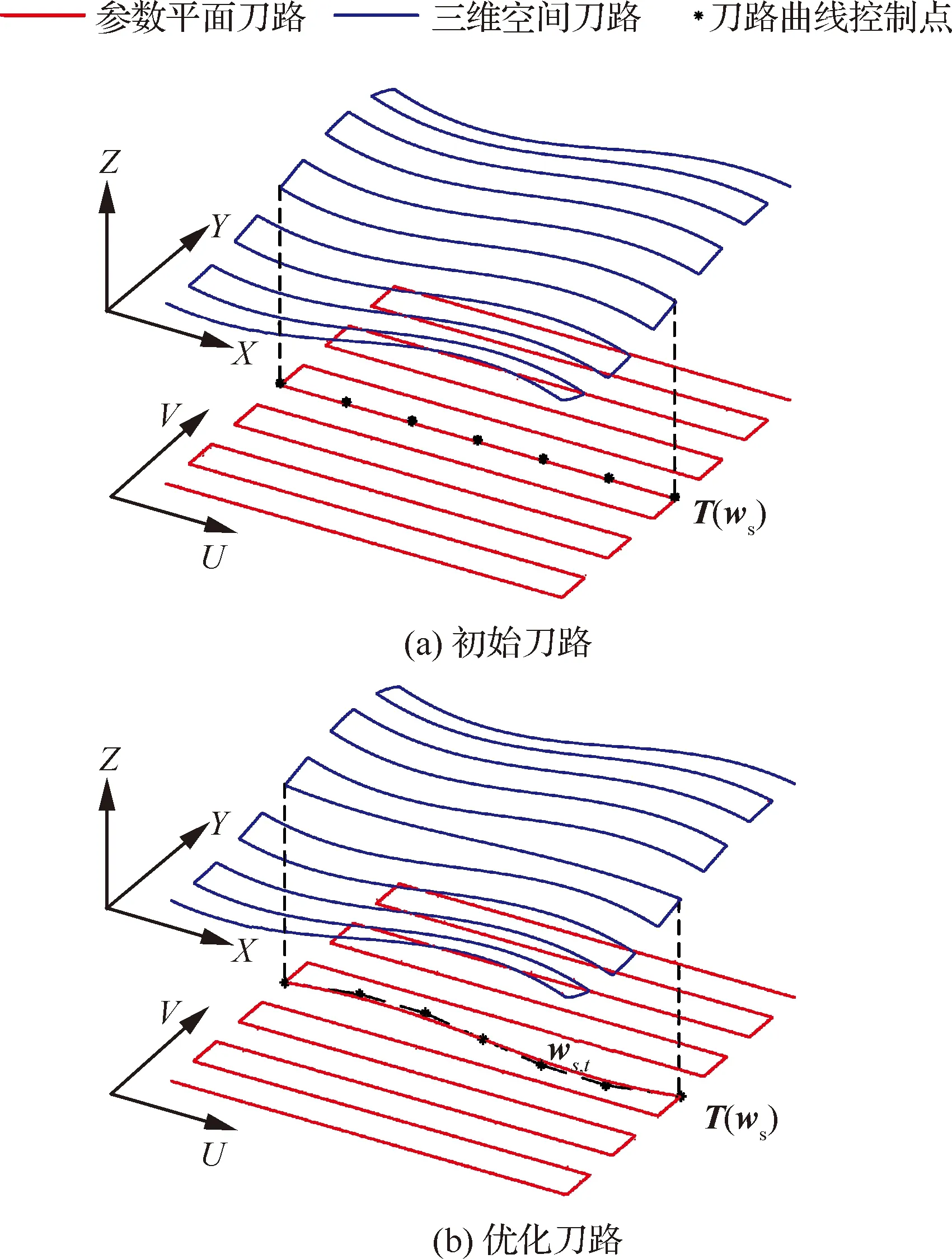
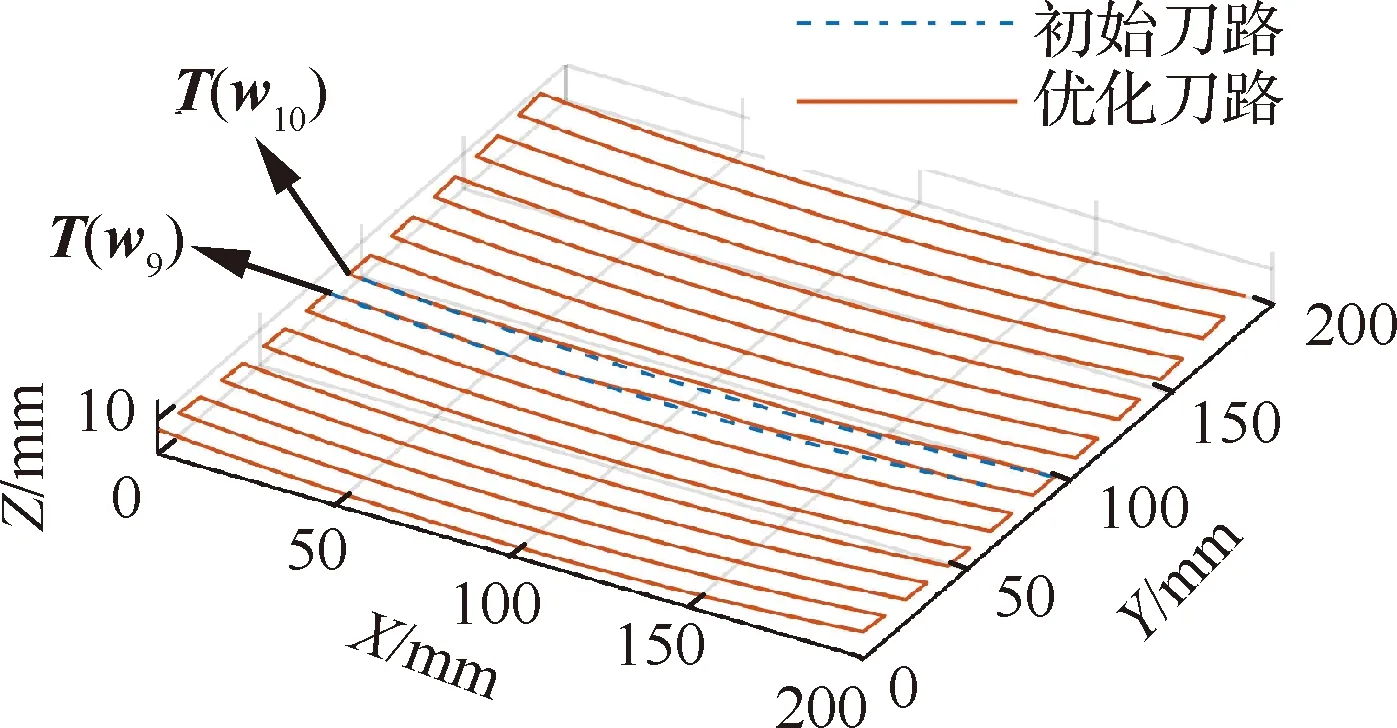
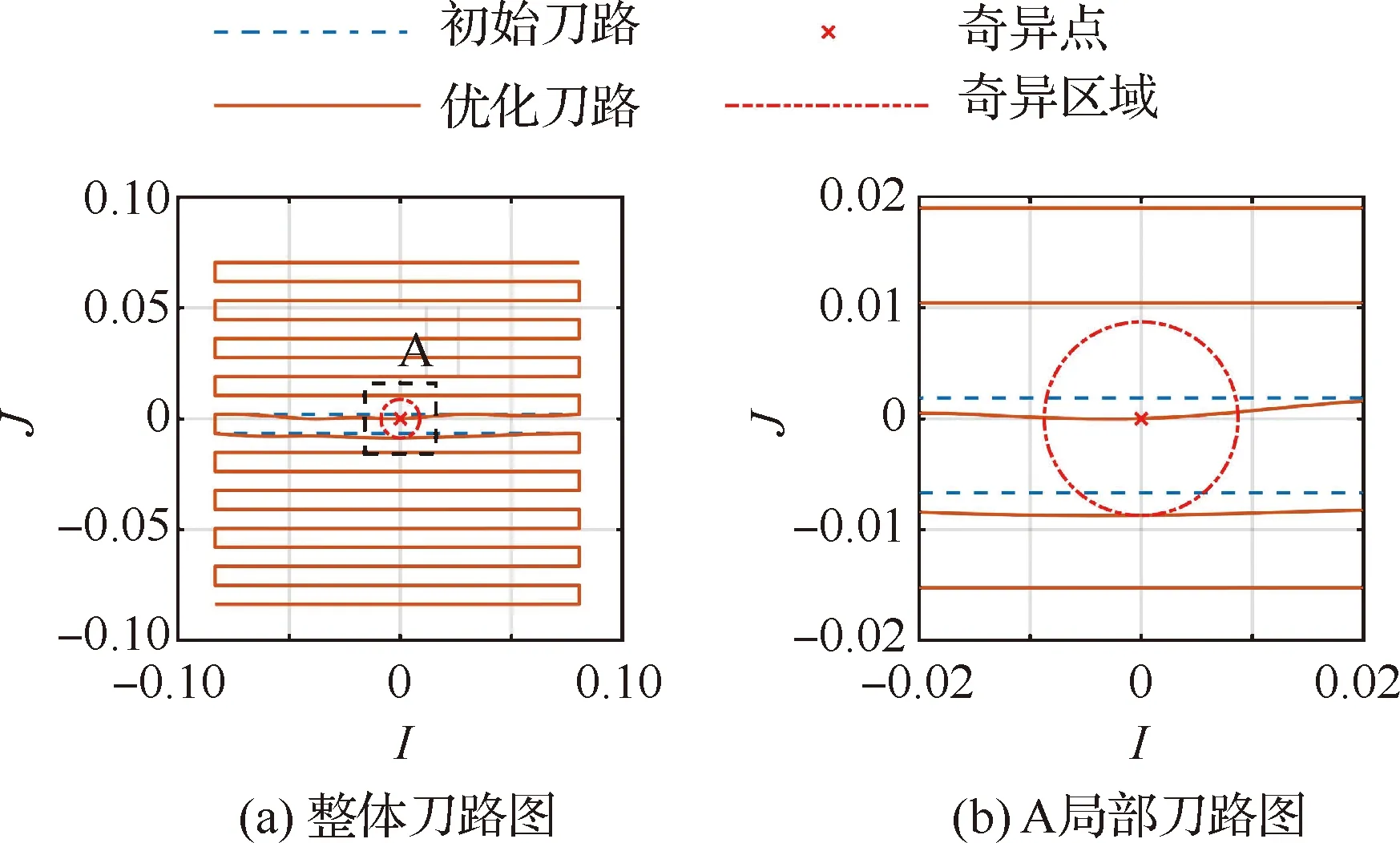
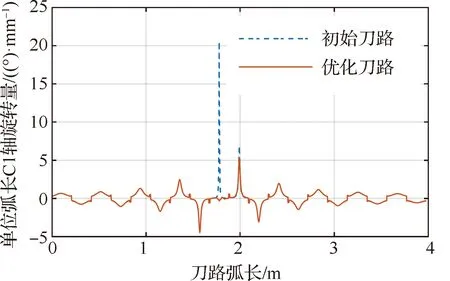
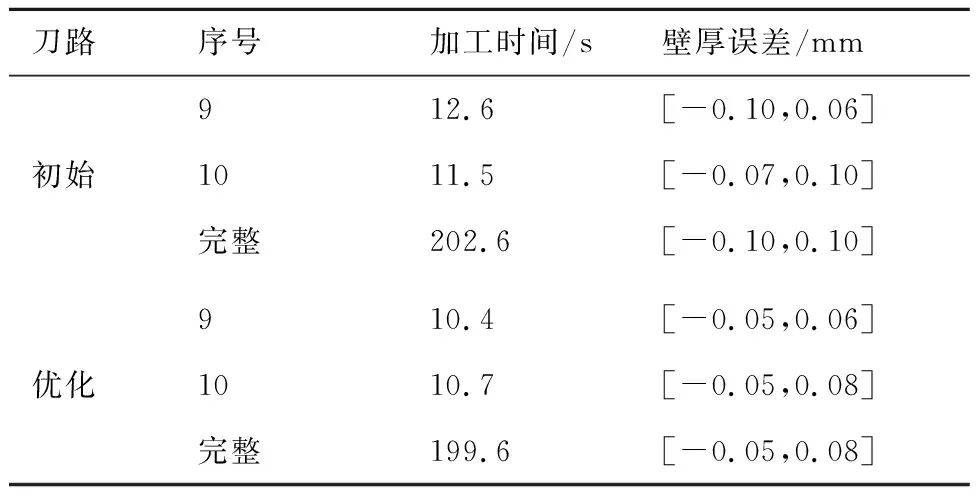
r

(8)

式中：a为当前刀路的径向切宽；r为刀具底刃半径。

2.2 刀具路径光顺性指标

在奇异区域内，铣削头A1轴的旋转量很小，旋转量变化值相应较小，但C1轴旋转量可能较大，造成C1轴在奇异区域内运动不连续。刀具路径优化的目的就是使得铣削头C1轴运动尽可能光顺。从上一节的分析可以知道，刀轴矢量在IJ平面内投影点(i,j)的方位角决定了C1轴的旋转量，因此可以(i,j)的方位角变化量来度量刀轴矢量的光顺性，如图3所示。

图3 刀轴矢量光顺性度量示意图Fig.3 Tool axis vector smoothness measure schematic

第l个刀位点Pl对应的刀轴矢量为Vl=[il,jl,kl]，从刀轴矢量Vl-1到Vl在IJ平面内的投影点方位角变化量为

(9)

考虑到在[-180°,180°]范围内C1轴存在两组解，当∠Vl-1OVl超过90°时，另一组方位角变化量小于90°的解为最优解。

在刀路单位弧长内方位角变化量越小，那么可以认为旋转轴运动越光顺，因此定义刀轴矢量光顺性度量为

(10)

式中：|Pl-Pl-1|为从第l-1个刀位点到l个刀位点的刀路长度；n为刀位点个数。

为了提高奇异区域内刀轴矢量的光顺性，需要调整刀轴矢量以避开奇异区域。由于镜像铣削刀路要求刀轴矢量与工件表面垂直，在修改刀轴矢量的同时，刀位点也必须随之修改，由此可能引起刀路的刀尖点运动不光顺。因此在度量刀轴矢量光顺性的同时，还需要度量刀尖点运动的光顺性。如图4所示，对于第l个刀位点Pl处的刀尖点轨迹转角定义为前后刀路的夹角，即

(11)

对应的，刀尖点运动光顺性可以表示为

(12)

图4 刀尖点光顺性度量示意图Fig.4 Tool tip point smoothness measure schematic

2.3 刀具路径优化方法

现有方法一般通过直接优化加工刀路的刀轴方向来避开加工奇异点，但对于镜像铣而言，刀轴矢量必须与工件表面垂直，因此只能通过在曲面上调整刀位点来实现奇异区域内的刀路优化。

为便于曲面上的刀路调整，将初始刀位点映射到曲面的UV参数平面内，并拟合为三次B样条，如图5(a)所示。第s条刀路在参数平面内用三次B样条表示为T(ws)，其中ws=[ws,1,…,ws,t,…,ws,m]∈m为第s条刀路的形状控制参数。刀路优化时，在满足切宽约束条件的前提下，以刀路刀轴矢量和刀尖点光顺性度量值的加权和最小化为目标，通过调整刀路形状控制参数ws即可实现刀路的优化，如图5(b)所示。

详细的刀路优化方法如下：

1) 在曲面上构造t条初始刀路，将刀位点投影到UV参数平面内并拟合为三次B样条T(ws),s=1,2,…,t。

2) 对于第s条刀路，根据刀路是否穿过奇异区域，确定刀轴矢量和刀尖点光顺性度量值的加权和:

(13)

式中：N为所有穿过奇异区域的刀路序号集合，s∈N表示该刀路穿过奇异区域，而s∉N表示该刀路不穿过奇异区域；λa为刀轴矢量光顺性权重；λt为刀尖点光顺性权重。λa和λt的大小会影响刀路优化结果。对于镜像铣削刀路，一方面刀尖点轨迹光顺性直接影响零件表面质量，另一方面在奇异区域附近刀轴矢量方位角变化量φl明显大于刀尖点轨迹转角θl，为了保证刀尖点光顺性对优化结果的约束能力，一般设定λt>5λa。在实际应用中，可根据刀路对刀轴矢量和刀尖点的光顺性要求适当调整权重。

图5 刀具路径优化方法Fig.5 Toolpath optimization method

3) 在满足镜像铣削切宽约束的前提下，以刀路刀轴矢量和刀尖点光顺性度量值的加权和为目标函数，将刀路优化转化为最小化问题：

s.t. 1.1r≤a≤1.9r

(14)

式(14)为约束优化问题，可以采用微分演化算法进行求解，求得每条刀路曲线控制点修正参数。

4) 根据优化后的刀路修正参数更新刀路曲线控制点，得到优化刀路。

3 实验验证

为了验证所提方法的有效性，在飞机蒙皮实验件上分别采用初始等参数刀路和优化刀路进行镜像铣削加工实验。

实验所用机床为图2所示的镜像铣削实验平台。蒙皮实验件材料为6061铝合金，尺寸如图6所示，毛坯壁厚为6 mm，切削区域为200 mm×200 mm型腔。实验所用刀具直径为20 mm，圆角半径为3 mm，底刃半径7 mm，2刃。实验主轴转速为8 000 r/min，进给率1 200 mm/min，名义径向切宽约为11 mm。采用微量润滑对加工区域进行冷却。

实验前，先采用等参数法生成19条初始刀路，如图7中的蓝色虚线所示。实验所用镜像铣削系统的插补周期为4 ms，C1轴最大转速3 000 (°)/min， 单步旋转量上限设定为25°，根据文献[10]的方法，可得奇异区域边界为ε≈0.5°，即A1<0.5°的范围为铣削头奇异区域，如图8中的红虚线所示。将初始刀路的刀轴矢量投影到IJ平面上，如图8中的蓝色虚线所示。并对初始刀路进行后置处理，得到单位刀路弧长C1轴的旋转量，如图9中的蓝色虚线所示。可以看到，第9、10条刀路会穿过机床的奇异区域，对应的C1轴旋转量也会发生突变，其中第9条刀路的最大单位弧长C1轴旋转量达到了20.54 (°)/mm。因此，需要对第9、10条刀路，采用2.3节提出的优化方法对加工刀路进行优化。考虑到实验所在奇异区域刀尖点轨迹转角较小，可适当提高刀尖点光顺性权重，即λt=10，而刀轴矢量光顺性权重设定为λa=1。优化后的刀路如图7中的橙色实线所示，其刀轴矢量在IJ平面内的投影和最大单位刀路弧长C1轴旋转量分别如图8和9中的橙色实线所示。优化后的第9条刀路刀轴矢量直接穿过奇异点，此时A1轴反向旋转，最大单位弧长C1轴旋转量下降到了-0.31 (°)/mm。而第10条刀路的刀轴矢量则避开了奇异区域，其最大单位弧长C1轴旋转量从6.90 (°)/mm下降到了5.34 (°)/mm。可以看到，本文所提的优化方法可以有效地优化奇异区域内的加工刀路，提高旋转轴运动光顺性。

实验时，先后采用初始刀路和优化刀路对实验区域进行加工，两次实验的目标壁厚分别为5 mm和4 mm，加工过程中实时采集工件剩余壁厚。加工后的零件表面如图10所示，两次实验的加工时间和壁厚误差统计如表1所示。

图7 实验刀路对比Fig.7 Experimental toolpath comparison

图8 实验刀路刀轴矢量在IJ平面上的投影Fig.8 Projection of tool axis vector of experimental toolpath on IJ plane

图9 刀路单位弧长C1轴旋转量对比Fig.9 Comparison of C1-axis rotation amount per unit arc length of toolpath

图10 加工表面对比Fig.10 Comparison of machined surfaces

从图10(a)和表1可以看出，采用初始刀路加工得到的工件表面在奇异点附近存在明显刀痕，零件剩余壁厚误差为[-0.10, 0.10] mm。这是因为在奇异区域内，初始刀路单位弧长的C1轴旋转量大，一方面造成了较大的刀尖点运动非线性误差，另一方面刀尖点移动速度明显减小，切削力发生突变，造成轴向切削力与支撑力不平衡，引起工件局部变形。两者既增加了壁厚误差，又使得奇异区域内的工件表面留下了刀痕。而优化后的刀路在奇异区域内的旋转轴运动较为光顺，壁厚误差降低到[-0.05, 0.08] mm，且奇异区域无明显刀痕。

表1 实验结果对比Table 1 Comparison of experimental results

对比表1中两次实验的加工时间可以看到，对于穿过奇异区域的第9、10条刀路，采用本文所提方法优化后，刀路旋转轴运动更加光顺，对应的加工时间分别减少了17.5%和6.9%，而整个实验区域加工时间减少了1.48%，奇异区域内的加工效率得到显著提升。

4 结 论

1) 通过建立镜像铣削系统铣削头和支撑头的旋转轴运动学模型，从微分运动的角度分析了奇异点产生的原因及其对加工质量的影响。分析结果表明在镜像铣削系统的有效行程内，铣削头存在的奇异点会影响加工质量和加工效率，支撑头无奇异点。

2) 在刀轴矢量和切宽约束下，基于光顺性指标的镜像铣削刀具路径优化方法保证了奇异区域内旋转轴运动的连续性，提高了加工质量和加工效率。