滚压强化表面状态特征的疲劳演化及抗疲劳机制研究进展
韩坤鹏,张定华,姚倡锋,*,谭靓,周征
1. 西北工业大学 航空发动机高性能制造工业和信息化部重点实验室,西安 710072 2. 西北工业大学 航空发动机先进制造技术教育部工程研究中心,西安 710072
航空发动机是一种高度复杂和精密的热力机械,被誉为“工业皇冠上的明珠”,它直接影响飞机的性能、可靠性及经济性,是一个国家科技、工业和国防实力的重要体现。随着我国新型飞机的研制以及军机数量的大幅增长和更新换代,发动机的需求也在逐年增加。现有航空发动机多采用高强度合金作为其主体结构和主承力构件,主要涉及发动机涡轮盘、压气机盘、压气机叶片、传统系统轴承等以疲劳为主要失效模式的关键构件,它们决定了航空发动机的性能。据统计,航空构件中疲劳失效占80%以上。因此,航空发动机构件的疲劳性能与航空发动机的使用寿命息息相关。
表面完整性是指为保持和提高材料的固有力学、物理、化学、生物等使用性能而需使材料表面所具有的不同于基体的特定状态和性能[1-2]。表面完整性内涵包括表面状态和表面性能两个部分,两者是相互关联的,表面状态决定或影响表面性能,表面性能体现或反映表面状态[1]。表面完整性概念自提出以来就受到普遍重视,研究成果得到广泛应用,特别是航空航天等涉及国防安全的领域。大量的试验研究已经表明表面完整性对构件疲劳性能有着重要的影响[3-9]。但是,切削加工零件表面存在着各种各样不可避免的因成形制造带来的缺陷,如加工刀痕、划伤、表层组织损伤、夹杂物等,使得零件的表面完整性远远不能满足其设计要求,需要进一步的表面处理来改善其表面完整性,进而提高零件的服役性能。
常用的表面强化工艺有喷丸、激光喷丸和滚压强化等,滚压强化指的是由液压驱动的滚压球(或者滚压轮)在工件表面进行滚压加工,使表面产生塑性变形,引起材料表层性能的改变,其原理图和实物图如图1所示,滚压设备可以安装在数控机床上,通过数控系统方便的控制滚压路径和精度,甚至可实现对复杂曲面的加工。滚压强化作为一种表面处理技术,能够引入较深的残余压应力、降低表面粗糙度和在表层形成纳米晶等优点,这些表面状态特征能够有效降低裂纹萌生和裂纹扩展速率,显著提高零件的疲劳性能[10-11]。但零件的表层残余应力、显微硬度等表面状态特征在服役过程中是不断演化的,表层残余压应力在某些情况下甚至会消失,这些改变会显著影响滚压强化工艺所带来的强化效果[12-13]。因此,揭示滚压强化表面状态特征的服役演化机理,对实现表面完整性控制,实现航空发动机长寿命高可靠具有重要的理论意义。
本文将重点阐述滚压强化表面状态特征的演化及抗疲劳机制的研究现状,总结研究中存在的仍然未解决的问题或者亟需要深入研究的问题,以期为滚压强化的研究和发展提供方向和思路方面的参考。

图1 滚压加工原理图及实物图Fig.1 Schematic diagram and physical drawing of deep rolling
1 残余应力演化研究现状
残余应力是当没有外力作用时,物体维持内部平衡存在的应力,产生残余应力的原因主要有三种,即不均匀塑性变形、不均匀热和不均匀相变。滚压强化工艺能使材料表层产生非均匀塑性变形,导致在不同部位之间出现相对的压缩或拉伸变形,从而在材料表层引入残余应力场[14],残余应力场的分布能显著影响裂纹萌生位置和扩展速率,在热载荷和机械载荷作用下,材料内部会发生微观塑性变形,导致残余应力场在零件服役过程中发生松弛,进而对零件的疲劳性能产生显著影响。鉴于残余应力场演化的重要影响,国内外学者针对此问题展开了广泛的研究。
Gill等[15]针对滚压Ti-6Al-4V以及IMI679在常温和高温下的低周疲劳残余应力演化进行了试验研究,结果表明残余应力松弛深度在400 μm到500 μm,常温低周疲劳情况下,残余应力松弛程度小于残余应力峰值的50%,高温低周疲劳试验情况下残余应力最大松弛程度可达到峰值残余应力的70%。可以看出,服役温度是残余应力演化的关键影响因素,Nikitin和Besel[16]针对奥氏体钢AISI304做了更为详细的研究,他们同样分析了机械载荷下温度对残余应力松弛的影响进行了分析,结果如图2所示,温度载荷为600 ℃时,残余应力热松弛量大约为30%(280 MPa),在室温到200 ℃之间,机械载荷引起的松弛量主要依赖于温度,而温度在200~600 ℃之间时,机械载荷引起的松弛量依赖于应力幅值。此研究结果可确定特定情况下何种因素对残余应力松弛起到关键作用,从而可通过控制该因素减缓残余应力松弛,达到提高构件寿命的目的。
此外,Nikitin和Besel[16]还分析了600 ℃纯温度载荷下以及600 ℃温度载荷和280 MPa机械载荷共同作用下的残余应力松弛行为,结果如图3所示,从两种情形下的残余应力松弛量可以分析得到纯机械循环载荷下残余应力松弛量。此研究结果量化了特定情况下热载荷和机械载荷导致的残余应力松弛量,对实现构件服役过程中残余应力松弛量的进一步精确控制十分有利。
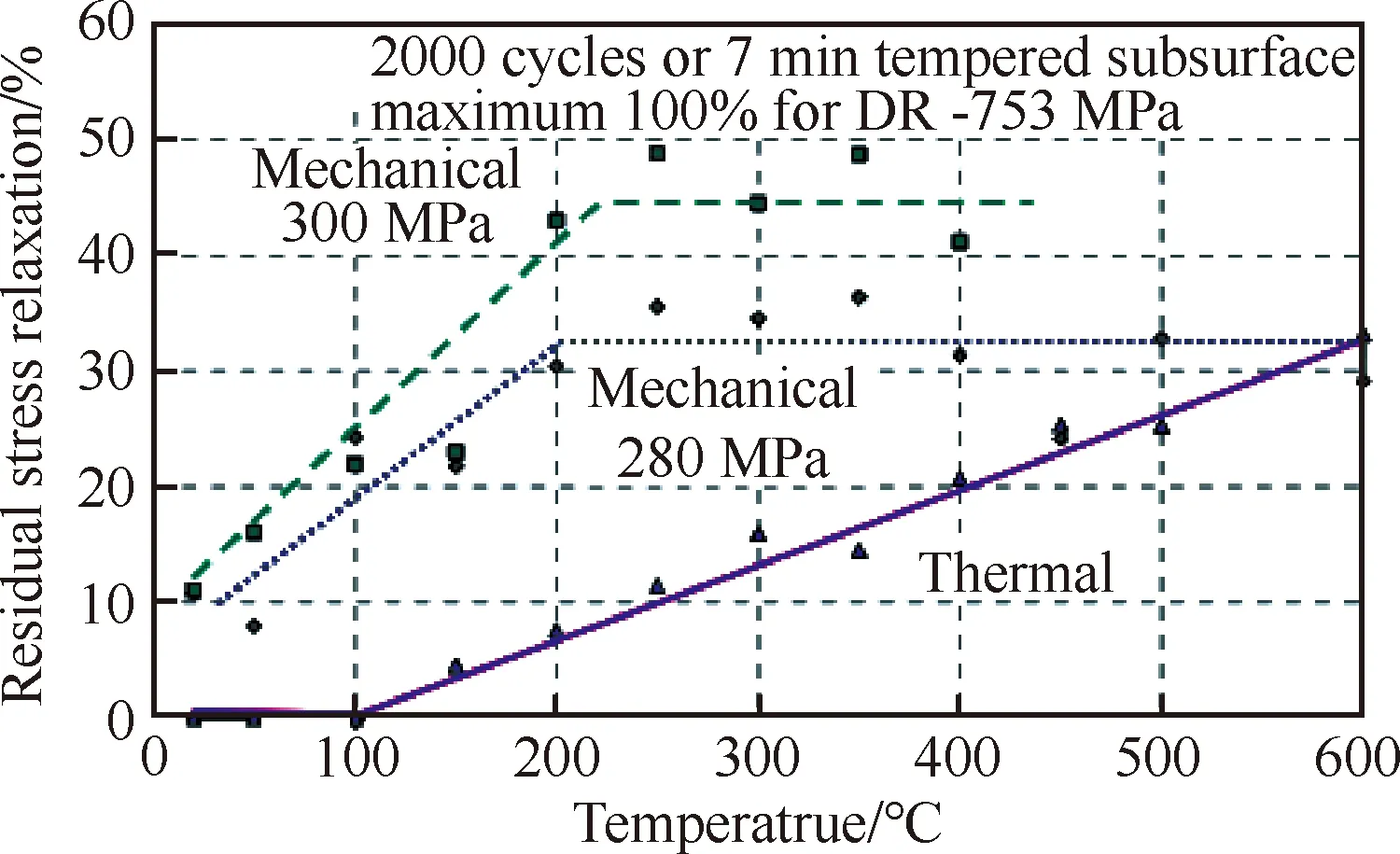
图2 机械载荷下温度对残余应力松弛的影响[16]Fig.2 Effect of temperature on residual stress relaxation under mechanical load[16]
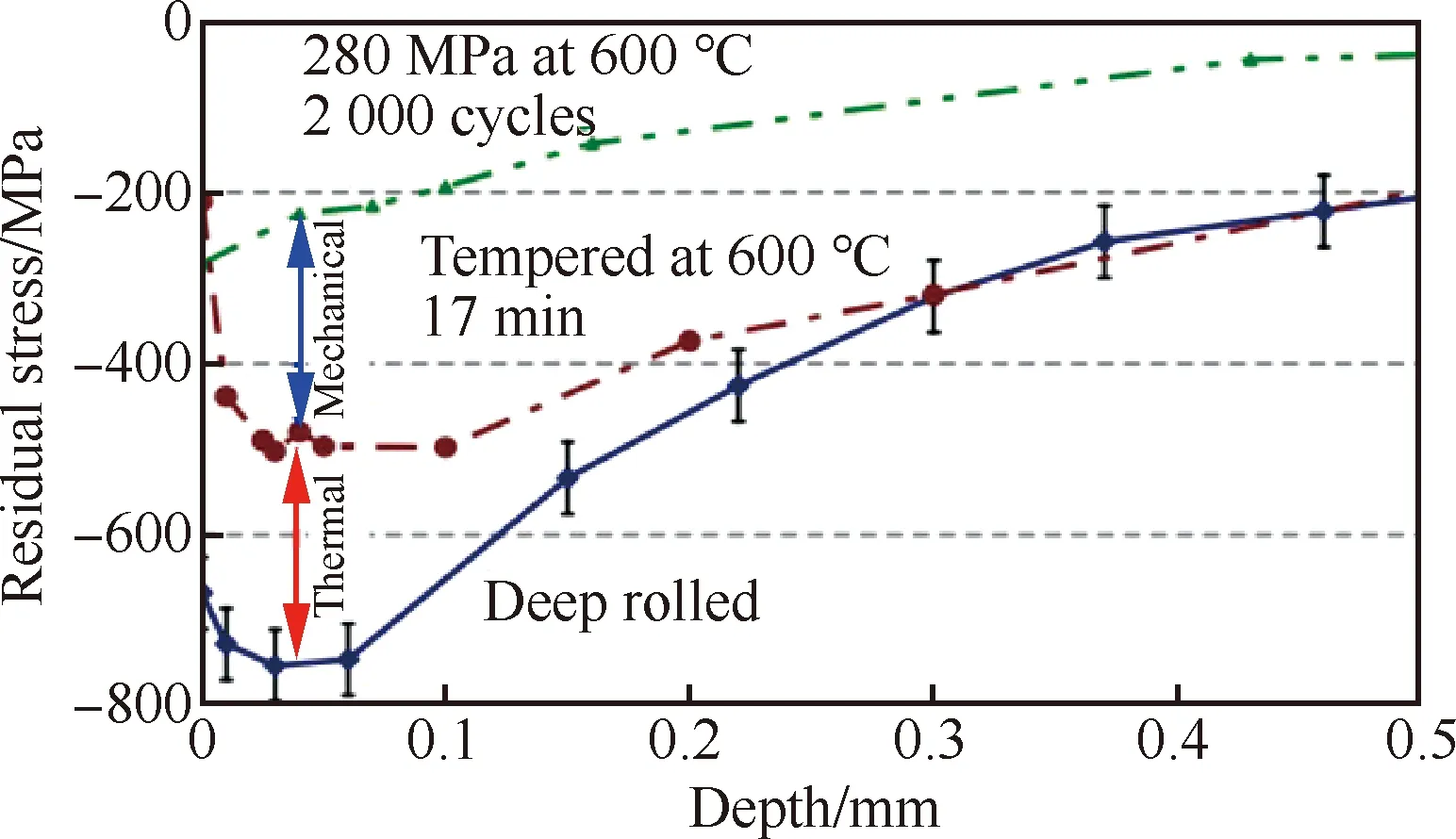
图3 机械载荷与温度载荷对残余应力松弛贡献量[16]Fig.3 Contribution of mechanical load and temperature load to residual stress relaxation[16]
Nikitin和Besel[16]还研究了残余应力在不同温度及不同暴露时间下的残余应力演化行为,结果如图4(a)所示,温度200 ℃时,残余应力经过100 h才出现松弛;而当温度为600 ℃时,仅1 h残余应力即发生了松弛。除了上述研究内容外,他们还对室温下应力幅值350 MPa时不同循环周次下的残余应力演化行为进行了分析,即仅考虑机械载荷对残余应力演化行为的影响,结果如图4(b)所示,残余应力随着循环周次的增加松弛量不断增加。
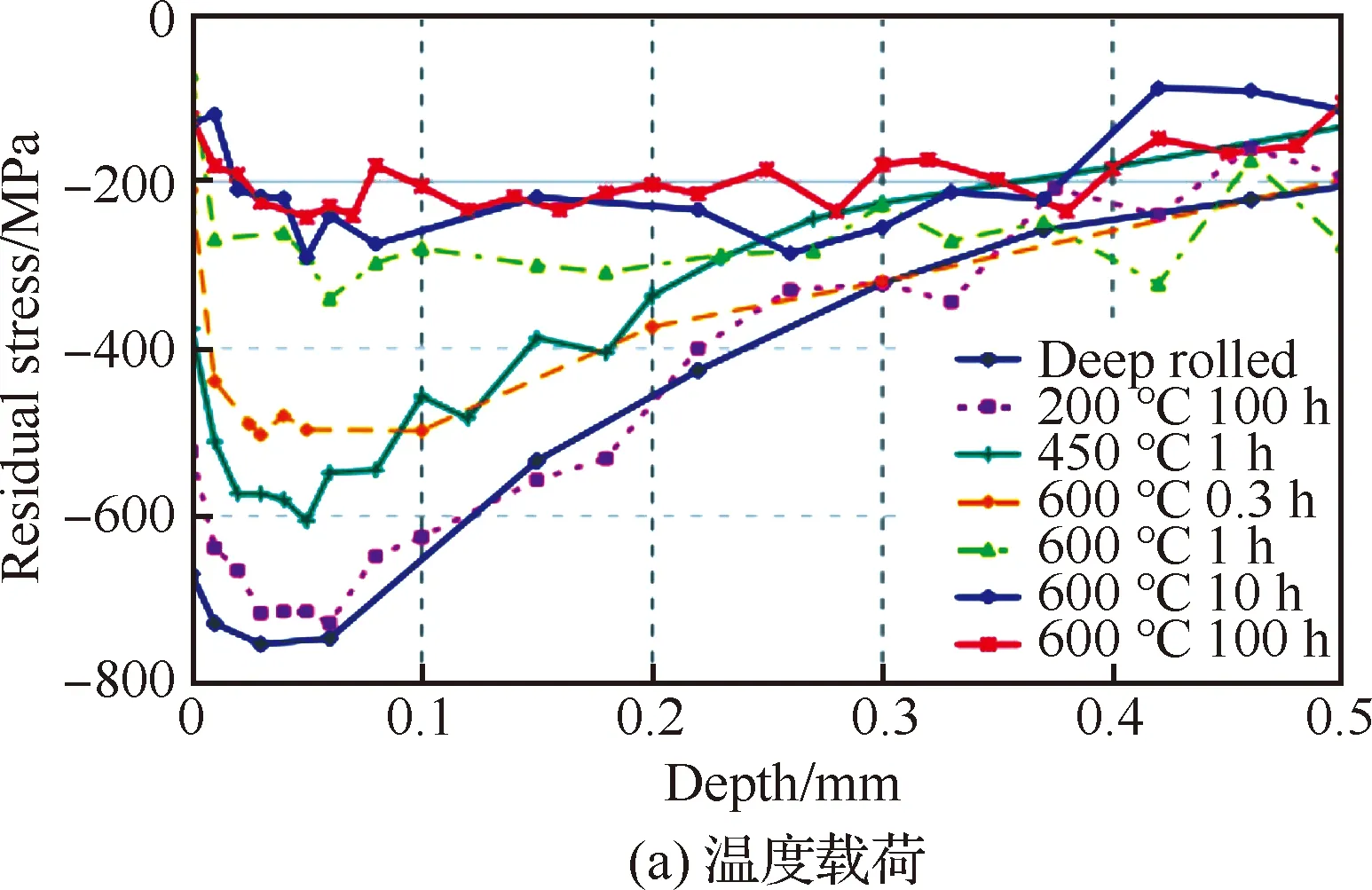
图4 温度和机械载荷对残余应力松弛的影响[16]Fig.4 Effect of temperature and mechanical load on residual stress relaxation[16]
因此,机械载荷对残余应力演化也有着十分重要的影响,学者们在这方面也进行了大量的研究,例如,Saalfeld等[17]研究了不同应力幅值(R=-1)对滚压SEA 1045钢圆棒试样残余应力演化的影响,结果如图5所示,随着应力幅值的增加,残余应力松弛的更快;对于990 MPa应力幅值来说,前500个循环,残余应力迅速减少,在之后的循环中逐渐完全消失。
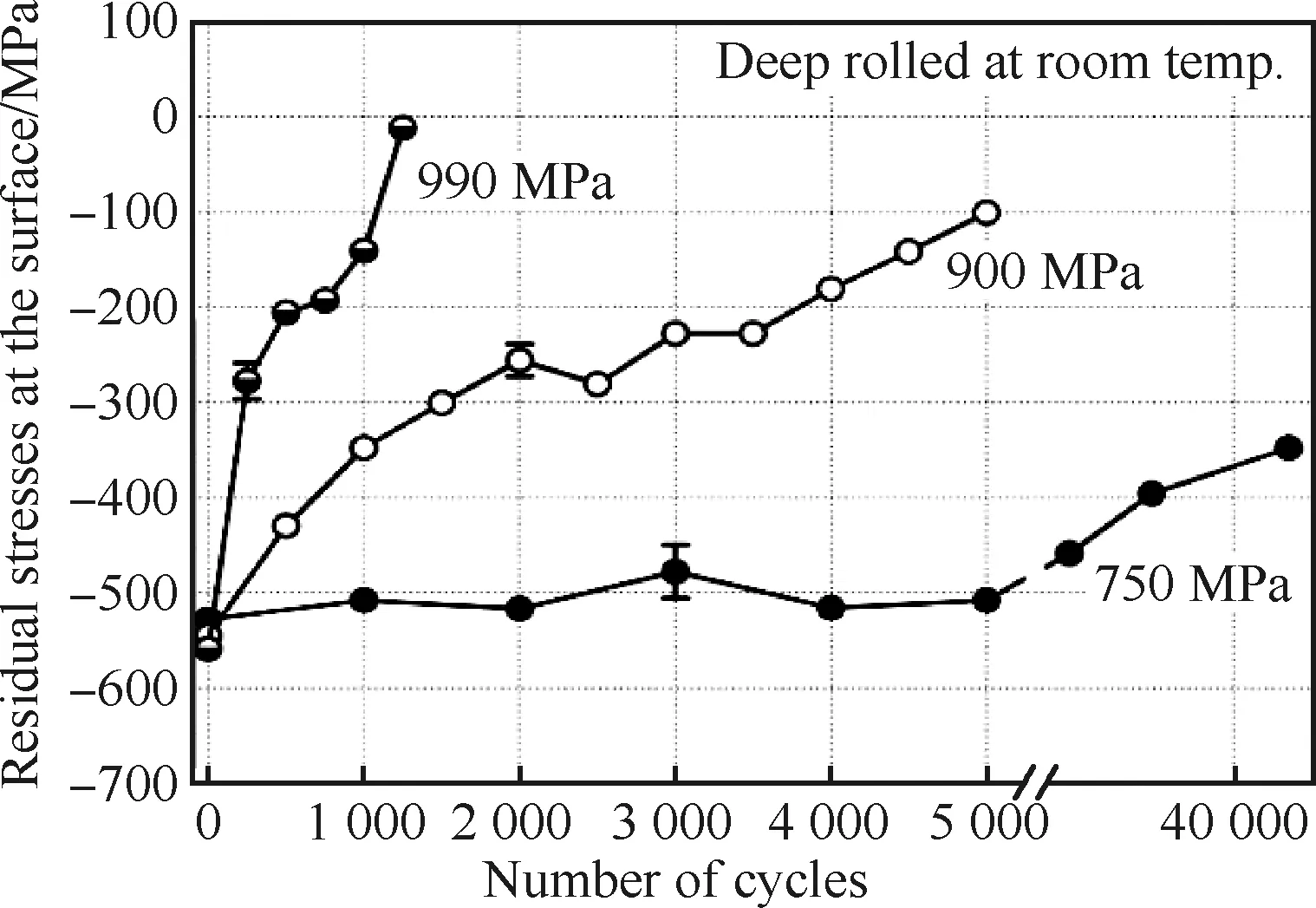
图5 应力幅值对残余应力松弛的影响[17]Fig.5 Effect of stress amplitude on residual stress relaxation[17]
Benedetti等[18]对喷丸工艺做了类似的研究,他们对3种喷丸参数加工的7075-T651 铝合金薄板反转弯曲疲劳下的残余应力演化开展试验研究,发现在低周疲劳下,残余应力在第一循环发生明显松弛,之后趋于稳定;在对应于5X106循环寿命的载荷下,即载荷较低的情况下,残余应力一直处于稳定状态。探求机械载荷对残余应力的影响规律对控制构件的受力,进而控制残余应力松弛量具有重要的理论指导意义。
除了热载荷和机械载荷对残余应力演化产生影响外,学者们还发现了其他一些影响因素。James[19]研究发现Al2219-T851表面强化处理产生的残余应力沿深度方向的分布梯度变化越大,残余应力松弛速率越快。此研究结果可为实现更高疲劳性能的残余应力沿深度方向的分布设计提供理论支撑。Chin等[20]发现加工工艺引起的硬化程度越高,残余应力松弛率及松弛量越大。此研究表明在改性强化中要控制表层的硬化量,较低的硬化量可减缓残余应松弛,进而有利于提高零件的疲劳寿命。Sano等[21]研究了不同R比对残余应力演化行为的影响,结果如图6所示,R比为0.1时,表面残余应力没有显著减少,R比为-1时,残余应力在第一循环显著减少,然后保持在大约150 MPa直到循环载荷结束。研究结果表明通过控制服役过程中所受载荷的形式可以有效控制残余应力的松弛行为。
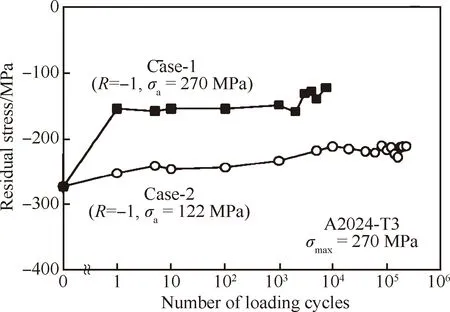
图6 R比对残余应力演化的影响[21]Fig.6 Effect of R ratio on residual stress relaxation[21]
You等[22]通过对缺口和无缺口平板试样的对比研究发现缺口能限制残余应力的松弛。此研究成果为残余应力松弛的控制提供了一条新的路径。
因此,残余应力的演化十分复杂,其与温度、应力幅值等因素都有着直接的关系,为实现残余应力在服役载荷下的演化行为的预测,有些学者针对不同情形下残余应力的演化建立了相应的预测模型。残余应力在热载荷下松弛是学者很早就注意到的现象,通过探索其中的规律,发现残余应力在纯温度载荷下的松弛行为符合Zener-Wert-Avrami方程:
(1)
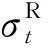
一些学者针对强化表面在热载荷作用下的松弛行为的研究发现试验数据与Zener-Wert-Avrami方程之间的预测值符合的很好[23-24]。
还有些学者通过分析残余应力在机械载荷下的松弛行为建立了相应的模型。例如,Kodama[25]根据喷丸试样表面残余应力演化试验数据建立了残余应力线性对数衰减模型,模型简单有效,但此模型只能预测第一循环之后的残余应力,其具体表达式为
(2)
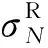
Han等[26]对焊接钢件在循环载荷下的残余应力演化行为进行了研究,针对不同载荷加载情况建立了残余应力松弛模型:
(3)
式中:σapp为加载应力;σy为屈服应力。
此模型可对包括第一循环在内的所有循环周次的残余应力松弛进行预测,但模型是针对焊接件建立,对其它情形是否适用有待进一步研究,但建模的思路可作为其他情形的参考。
Zhuang和Halford[27]考虑残余应力大小和分布、硬化程度、交变应力、平均应力的大小以及加载循环周期数建立了低塑性滚光加工零件表面残余应力演化经验模型,其表达式为
(4)
式中:σa为应力幅值;R为应力比;Cw为硬化量;A2和m2为基于循环应力应变响应的材料常数;B为残余应力松弛率。
此模型虽考虑了更多的影响因素,有助于提高模型的适用范围和预测精度,但模型仅通过有限元分析数据进行了验证,缺少真实试验数据的验证,有必要结合具体试验数据对模型进行进一步的验证或修正。
另外,一些学者发现第一循环残余应力松弛规律和机理有别于后续的循环周次,残余应力在第一循环的松弛量有时很难用准确的公式去精确表达[28-29],所以有学者探索了新的方法针对第一循环的残余应力演化进行建模,例如,Mauduit等[30]研究了喷丸TRIP 780薄板试样在反转弯曲循环载荷下的残余应力松弛现象,采用有限元法建立了第一循环载荷内残余应力松弛行为的模型,揭示了残余应力松弛机理。但是,模型虽可以对不同受力情形下的第一循环残余应力松弛进行预测,仿真中却主要考虑了喷丸引入的残余应力,没有充分考虑喷丸对表层带来的硬化效果,表层的硬化会对材料的本构产生影响,影响仿真结果的准确性,因此,此仿真方法还有待进一步完善。
从上述针对残余应力演化行为的试验研究和预测建模可以看出,目前针对滚压强化残余应力演化的研究相对来说比较少,且研究的内容基本上都是对强化表面残余应力演化进行研究,很少涉及到不同深度的残余应力的演化,也未见有学者针对不同深度的残余应力演化建立模型,不同深度的残余应力演化的建模涉及的因素会更多,简单的经验建模精度很难有保证,需深入研究残余应力松弛的机理,分析不同深度残余应力松弛之间的相互影响,选取合适的理论和方法才能建立有效的针对不同深度的残余应力演化预测模型。
2 显微硬度演化研究现状
显微硬度是材料抵抗压入弹塑性变形抗力的一个重要性能,直接反映了材料在加载过程中的应力应变与卸载后的弹性回复及塑性压痕特征,而且在工程中非常便于应用,因此在表征表层力学性能特征时多采用显微硬度来间接反映表层的强度、塑性和抗弹塑性变形能力[31]。滚压强化可以使材料表层发生硬化,使表层硬度提高,并沿深度方向逐渐下降到基体硬度。硬度的提高可以提高零件的耐磨损性能,有益于材料的抗疲劳性能的提高,但材料在服役环境下,由于力和热的作用,材料内部位错滑移等现象会对材料的硬度产生影响,使材料硬度不断发生变化,对零件的疲劳性能产生影响,目前笔者未发现有针对滚压强化硬度演化方面的研究,现就学者对其他工艺的研究情况进行综述和分析,为滚压强化硬度演化的研究提供参考。
Zaroog等[32]研究了喷丸强度为0.005 4A、0.006 7A和0.009A的2024-T351铝合金薄板在两种载荷下的疲劳演化行为,结果如图7所示,发现第一循环后,载荷为15.5 kN时,硬度分别降为176 HV、188 HV和196 HV,而载荷为30 kN时,分别降为170 HV、181 HV和188 HV; 10 000 循环后,载荷为15.5 kN时,显微硬度分别降为143 HV、147 HV和155 HV,而载荷为30 kN 时,分别降为137 HV、139 HV和141 HV。可以看出机械载荷的增加会导致显微硬度下降量的增加。
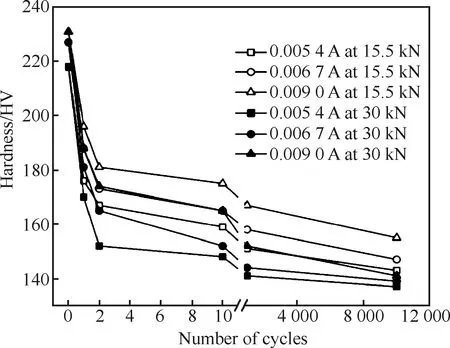
图7 不同机械载荷幅值对喷丸显微硬度的 演化的影响[32]Fig.7 Effect of different mechanical load amplitudes on microhardness evolution of shot peening[32]
Isa等[33]也就机械载荷对显微硬度的影响问题展开了研究,结果如图8所示,他们通过分析喷丸碳钢狗骨试样52 MPa(屈服应力的20%)和208 MPa(屈服应力的80%)循环载荷下显微硬度的变化,发现循环周次较低时显微硬度的变化是无序的,随着循环周次的增加显微硬度呈现下降趋势。
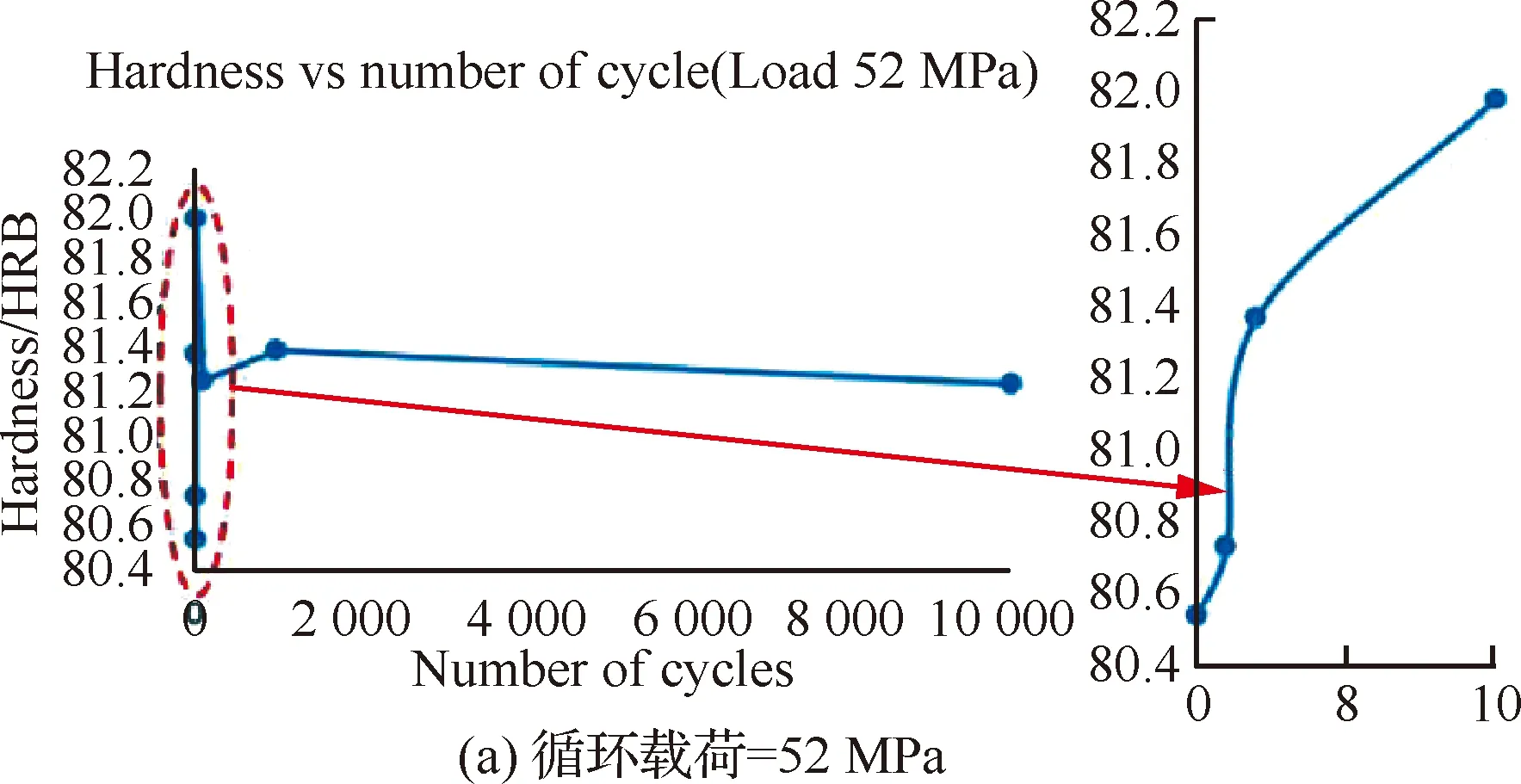
图8 低循环周次下显微硬度的演化[33]Fig.8 Microhardness evolution in low cycles[33]
钟丽琼等[34]研究了载荷形式对显微硬度演化的影响,对比了喷丸和未喷丸TC11拉压以及拉拉两种高周疲劳试验过程中显微硬度的变化,结果如图9所示,拉压疲劳后,未喷丸试样表层硬度值沿深度方向呈小幅上升趋势,喷丸试样表层硬度沿深度方向出现明显的梯度降低的现象;拉拉疲劳后,与拉压疲劳相比,未喷丸试样和喷丸试样表层硬度值都有所增加,且未喷丸试样表层硬度沿深度方向梯度上升趋势明显,喷丸试样表层硬度沿深度方向梯度变化不明显,但拟合的曲线呈现平缓下降趋势。
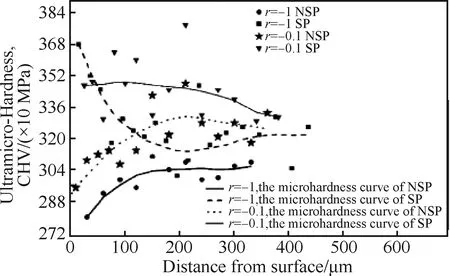
图9 不同载荷形式对显微硬度演化的影响[34]Fig.9 Effect of different loading forms on microhardness evolution[34]
Li等[35]研究了械研磨工艺形成的纳米层对碳钢疲劳行为的影响,结果如图10所示,显微硬度相对来说十分稳定,只是出现了轻微的软化。他们指出这一现象与超细晶材料在循环低应力载荷下初始应变能的释放以及晶粒内位错密度降低、位错滑移、部分晶界滑移产生的硬度下降是同样的原理。
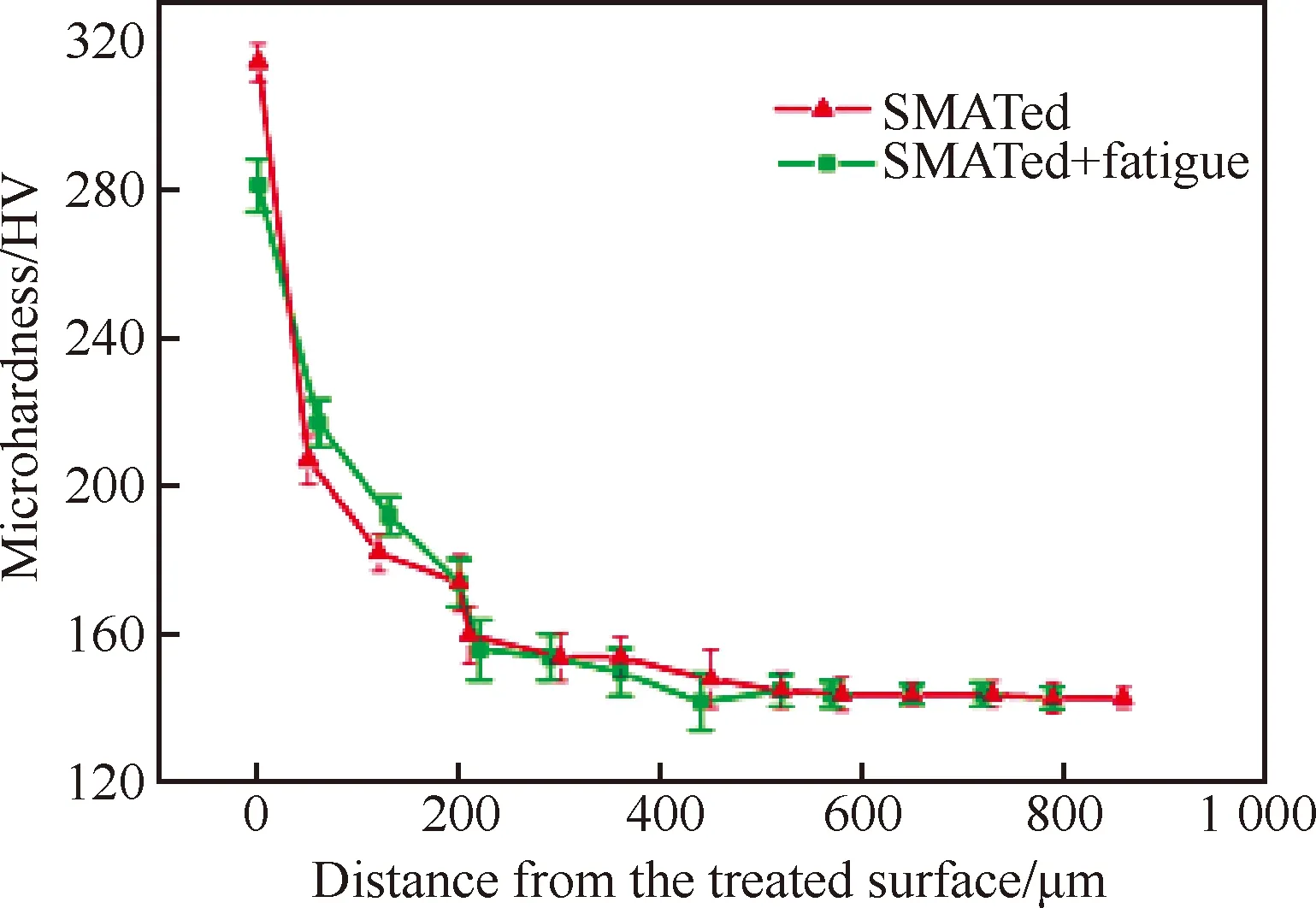
图10 机械研磨工艺显微硬度的疲劳演化[35]Fig.10 Fatigue evolution of microhardness induced by mechanical attrition treatment[35]
综上可知,目前不仅很少有学者对滚压硬度的演化开展研究,国内外学者对其他工艺,如喷丸、研磨等工艺的显微硬度在不同载荷及循环周次下的演化的研究方面也不够深入,大部分学者还是仅对演变规律做了观测描述,很少见学者从组织的角度去分析硬度的变化,因此,需要针对组织变化与硬度的变化之间的内在关联展开深入研究,揭示显微硬度的演化机理。
3 微观组织演化研究现状
滚压强化能够使材料表层发生塑性变形,增加位错密度,细化晶粒,但在服役环境中,由于热、力作用,表层组织的形态大小等都会发生变化,组织的变化与材料的疲劳性能息息相关,例如,晶粒细化可以增加晶界的数量,而晶界对裂纹的扩展起到一定的阻碍作用。因此,揭示微观组织的演化机理对提高零件的疲劳性能十分关键。
国内外学者针对疲劳过程中微观组织演化问题开展了大量研究。有学者针对微观组织在高温下的稳定性进行了研究,如Altenberger等[36]使用透射电镜观测了AISI 304和Ti-6Al-4V滚压加工后近表面纳米组织在高温下的变化,结果如图11所示, AISI 304的纳米组织最高可在600~650 ℃仍然稳定,而Ti-6Al-4V的纳米组织最高在650 ℃仍然稳定,且短时间承受900 ℃的高温,600 ℃以下保温5~20 min微观组织没有发生任何可见的变化。由此可见,不同的材料的微观组织在温度载荷下的演化有很大差异。另外,更值得说明的是此项研究的出发点是表面改性引入的表面状态和性质在服役条件下是否仍然稳定,如果表面改性引入的满足要求的表面状态和性质在服役条件下很快发生改变,那么对疲劳寿命的提高作用将微乎其微,这就对表面完整性设计提出了更高的要求。

图11 TC4及AISI304滚压微观组织的高温稳定性[36]Fig.11 High temperature stability of microstructure of deep rolling TC4 and AISI304[36]
还有学者针对微观组织在机械载荷下的演化进行了研究,毛淼东[37]研究了超声滚压TC4钛合金微观组织的低、高周疲劳演化行为,结果如图12所示,应变幅处于较低的0.4%水平时,晶粒大小没有明显变化,而应变幅提高到较高的1.2%时,TC4表面的纳米晶粒发生明显粗化。

图12 超声滚压TC4微观组织疲劳演化[37]Fig.12 Fatigue evolution of microstructure in ultrasonic deep rolling TC4[37]
Yan等[38]对热轧AZ31B镁合金微观组织在拉拉疲劳下的疲劳演化进行了研究,结果如图13所示,开始时的等轴晶粒在5000循环时迅速减小,并指出这是由疲劳过程中的动态再结晶引起的。此研究揭示了微观组织在不同阶段的演化规律,微观组织在整个寿命周期中的演化机理的清晰认知对表面完整性设计、提高构件的疲劳寿命具有重要意义。

图13 AZ31B镁合金拉拉疲劳过程中的晶粒细化[38]Fig.13 Grain refinement of AZ31B Magnesium Alloy during tension-tension fatigue[38]
Martin等[39]对正火SAE 1045喷丸后在循环应力载荷下微观组织的变化进行透射电镜观察,发现在450 MPa高应力幅值下变质层由于位错排列的改变导致微观组织中产生了胞状结构,在应力幅值较低的350 MPa和400 MPa仍然有晶胞结构的形成,但是晶胞结构较分散,而应力幅值为300 MPa时无晶胞结构形成。
Altenberger等[40]研究发现320 MPa机械载荷作用下,AISI304滚压强化试样表面微观组织中的马氏体成分在疲劳过程中呈现增加的趋势,而喷丸试样却没有发生这种现象,如图14所示,并指出这是由较高的缺陷密度(位错)引起的。他们还发现喷丸加工的AISI304试样形成的位错晶胞十分分散,并分析得出这是由于AISI304中奥氏体堆垛层错能较低,需要在较高应力幅值下才能出现位错晶胞结构所造成的。
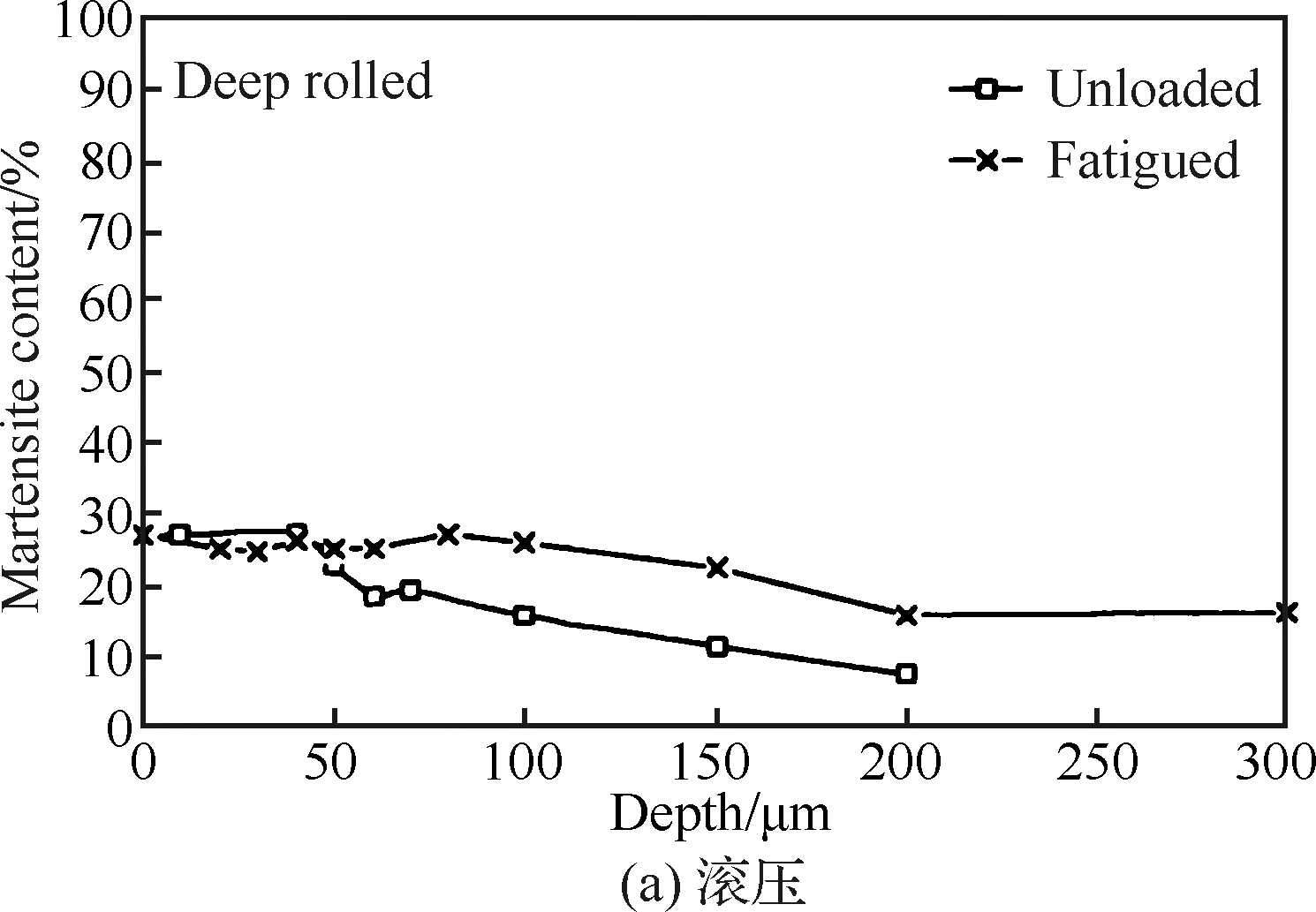
图14 滚压和喷丸组织疲劳过程中马氏体占比变化[40]Fig.14 Change of martensite proportion in microstructure of deep rolling and shot peening during fatigue process[40]
另外,他们通过分析还发现同一循环周次不同深度的组织形态也不一样,如图15[40]所示。值得注意的是研究内容涉及到的不同深度微观组织的演化在其他文献中很少见到,揭示其演化机理可对表面完整性分层设计提供理论依据。

图15 不同深度组织形态[40]Fig.15 Morphology of microstructure at different depths[40]
分析机械载荷对微观组织演化的影响不难发现,机械载荷下微观组织演化比较复杂,不同材料及载荷的大小差异都会对微观组织在机械载荷作用下的演化产生很大的影响,有时候甚至会出现完全相反的结果。
综合分析温度和机械载荷对微观组织疲劳演化的影响可知,目前学者虽对微观组织在疲劳过程中的演化进行了研究,但涉及到关于滚压强化工艺表层微观组织的疲劳过程演化规律的研究还是较少,对滚压工艺微观组织疲劳演化规律的认知尚不全面和清晰,比如疲劳过程中织构变化、孪晶类型、滑移模式等问题还有待研究。因此,需要针对滚压强化工艺微观组织疲劳过程中的演化展开深入的研究,进一步揭示其微观组织在疲劳过程中的演化机理。
4 表面状态抗疲劳机制研究现状
滚压强化目前已有一定的应用,在提高零件疲劳性能方面成效显著,弄清楚滚压强化带来的残余压应力层等特征是如何影响零件的性能的以及哪一个特征在哪个阶段的影响最为关键对优化滚压强化参数、进一步提高零件的寿命和可靠性显得尤为重要。
国内外学者对包括滚压强化在内的不同的表面强化方法进行了积极的研究,Yao等[41]研究了铣削、喷丸和抛光三种工艺的组合加工对TB6钛合金疲劳性能的影响,发现疲劳寿命与粗糙度值成反比;喷丸引入的残余应力和硬化层可显著提高材料疲劳性能,适当的组合可把裂纹萌生位置从表面转化为表面以下,如图16所示。
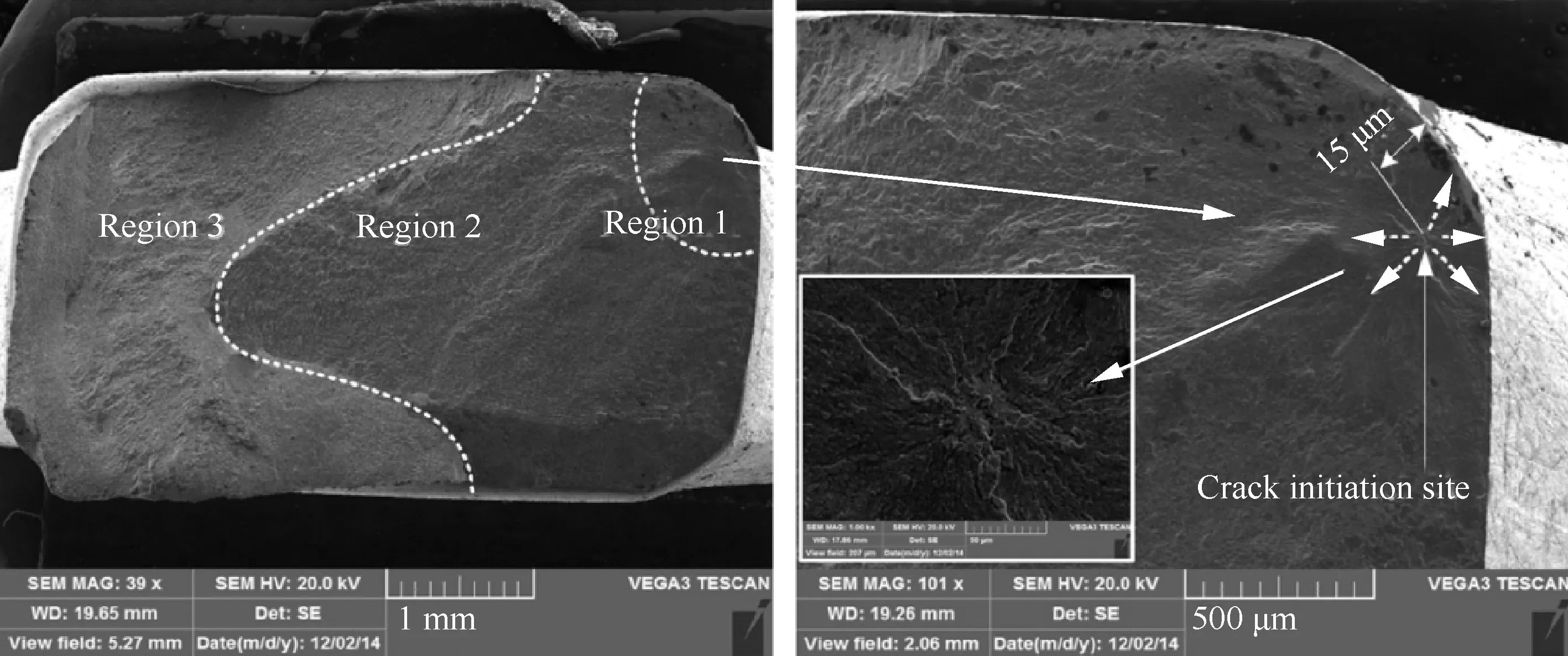
图16 裂纹从表面下萌生(加工顺序:铣削-喷丸-抛光-喷丸)[41]Fig.16 Crack initiation from subsurface (machining sequence: milling-shot peening-polishing-shot peening)[41]
Wu等[42]研究了喷丸强化对GH4169车削试样疲劳性能的影响,试验结果表明喷丸强化以后寿命显著提高,且同样发现喷丸引入的残余应力和表面硬化是寿命提高的关键因素;另外,由于喷丸引入的较高的表面粗糙度对寿命有不利影响,他们还研究了喷丸后抛光对疲劳寿命的影响,发现抛光以后寿命可进一步提高,从图17可以分析出寿命提高的原因,由于较低的表面粗糙度,疲劳源由原来的多源起始变为单源起始。

图17 裂纹萌生位置[42]Fig.17 Crack initiation position[42]
以上两位学者的研究不同于其它文献之处在于针对多种工艺的组合加工引起的疲劳失效及抗疲劳机理的改变进行了详细的研究,为提高构件疲劳性能的加工工艺及加工顺序的选择提供了理论依据。
另外,不少学者针对残余应力对抗疲劳机制的影响开展了更为深入的研究,Sun等[43]研究分析了残余应力沿深度的分布对裂纹萌生的影响,如图18所示,在外载荷超过疲劳极限的位置,裂纹开始萌生,但当适宜的加工参数引入更大的残余应力时,就需要更大的外载荷使裂纹萌生,且使得裂纹萌生位置出现在更深的位置,有效的提高了材料的疲劳性能。
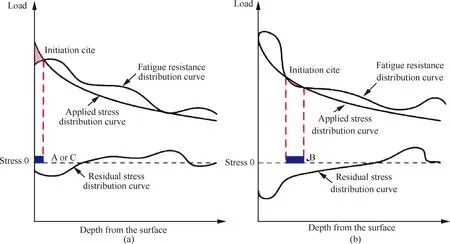
图18 残余应力分布对裂纹萌生的影响[43]Fig.18 Influence of residual stress distribution on crack initiation[43]
还有学者进一步分析了残余应力对裂纹扩展的影响[44],如图19所示,喷丸工艺引入的残余应力使得材料的疲劳极限增加,裂纹止裂区域扩大,但喷丸工艺与未喷丸工艺的疲劳极限曲线随着裂纹长度的增加逐渐收敛到一起,表明当裂纹长度较长时,残余应力对裂纹止裂的作用越来越弱。
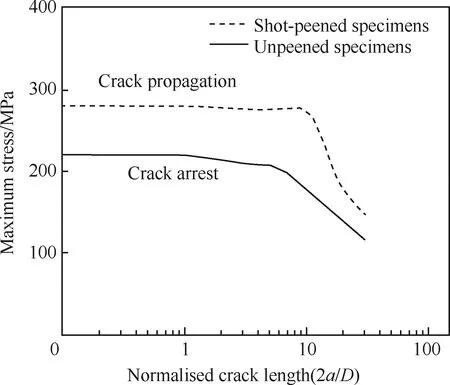
图19 残余应力对裂纹扩展的影响[44]Fig.19 Effect of residual stress on crack growth[44]
Galzy等[45]也针对滚压工艺引入的残余应力对疲劳性能的影响进行了研究,结果如图20和21所示,残余应力在第一循环的松弛使得靠近表面的残余应力变为拉应力,不再对阻碍裂纹萌生起作用,另外,当裂纹尖端应力强度因子超过一定值时裂纹才会扩展,当外载荷为5300 Nm时,裂纹会一直扩展,当外载荷为4500 Nm时,裂纹扩展到1 mm时将会停止扩展,但当裂纹长度扩展到1.5 mm时,过载情况下裂纹将不再停止扩展。
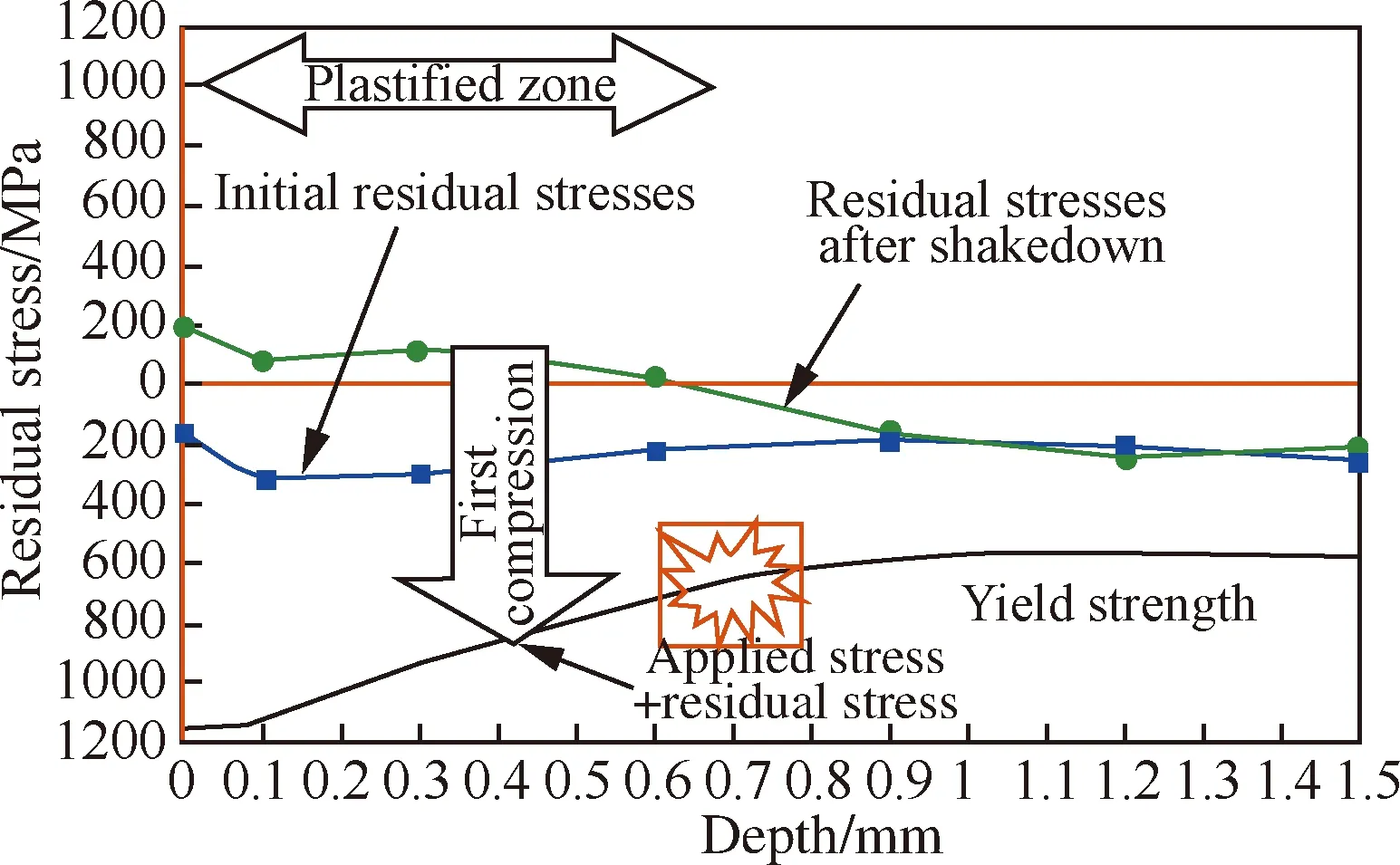
图20 残余应力的松弛对裂纹萌生的影响[45]Fig.20 Effect of residual stress relaxation on crack initiation[45]
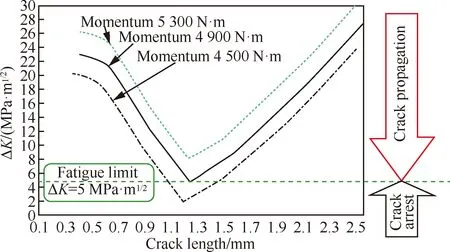
图21 应力强度因子对裂纹扩展的影响[45]Fig.21 Effect of stress intensity factor on crack growth[45]
Nie等[46]研究了TC11钛合金激光喷丸高周疲劳行为,指出在裂纹萌生阶段,由于残余压应力能够抵消一部分工作应力,阻碍裂纹萌生,提高裂纹萌生寿命;在裂纹扩展阶段,残余压应力能够降低应力强度因子,增加微裂纹闭合力,显著抑制裂纹的扩展。
他们还分析发现细化的晶粒能够降低晶粒滑移,阻碍滑移带的形成,大量晶界可以阻碍裂纹的扩展,特别是高周疲劳后期,随着残余应力的松弛,微观组织的改变更是疲劳性能提高的主要因素。Deng等[47]的研究也表明了组织对疲劳性能的重要性,他们对GH4169不同热处理组织疲劳裂纹扩展进行了研究,经过总结分析,提出了GH4169 裂纹扩展三阶段模型,如图22所示,在第一阶段,两种组织的裂纹均在氧化杂物处萌生并穿晶扩展,在第二阶段,直接时效热处理组织由于晶界氧化物作用表现为沿晶扩展,而特殊热处理组织,由于晶界δ相的阻碍作用,裂纹呈现穿晶和沿晶混合的扩展方式,第三阶段,δ相的作用仍然十分明显,直接时效热处理组织为沿晶断裂且周围出现很多微裂纹,而特殊热处理组织的主裂纹以穿晶断裂方式扩展且周围没有小的微裂纹产生。
从现有研究来看,国内外学者关于表面状态抗疲劳机制的研究主要集中在不同载荷下(如不同平均应力、不同温度等)残余应力分布、硬化层、应力集中等因素对裂纹源数量及位置、裂纹萌生和扩展速率等的影响,但鲜有学者在此研究基础上考虑表面状态特征的耦合影响作用,建立相应的疲劳寿命预测模型,因此,十分有必要针对滚压强化工艺,研究其对疲劳性能的影响,提取对疲劳寿命有着重要影响的滚压强化表面状态特征,建立疲劳寿命预测模型。
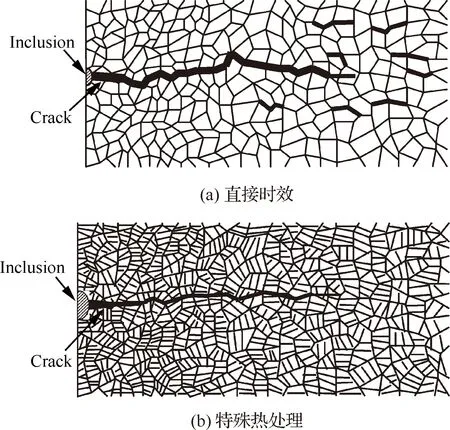
图22 裂纹扩展三阶段模型[47]Fig.22 Three-stage model of crack growth[47]
5 疲劳寿命预测研究现状
疲劳寿命预测的实现,可以避免产品设计阶段每次设计出新的结构都要做疲劳试验,节约大量的试验费用,还能为产品的检修周期、保修时间等提供重要的参考。由于疲劳寿命预测的重要意义,国内外学者针对疲劳寿命预测展开了大量的研究。
对于单轴疲劳而言,基于应力的寿命预测方法广泛应用于高周疲劳的预测,其方程如式(5)所示,此公式通常被称作Basquin方程:
σa=σ′f(2Nf)b
(5)
式中:σ′f为疲劳强度系数;b为疲劳强度指数;Nf为疲劳寿命。
对低周疲劳而言,通常使用基于应变的寿命预测方法,其公式为
(6)
式中:εa为应变幅值;εea为弹性应变幅值;εpa为塑性应变幅值;ε′f为疲劳延性系数;c为疲劳延性指数;E为弹性模量。
需要注意的是式(5)和式(6)是在对称循环载荷下的疲劳试验获得,而真实情况下载荷往往是不对称的、随机的,需要对公式进行修正。针对不对称载荷,即平均应力不为0的情形,学者们提出了不同的解决方案。对于载荷平均应力不为0的高周疲劳寿命预测,比较著名的修正方程有Goodman方程、Gerber方程和Soderberg方程等,其中Goodman方程表达式为
(7)
式中:σ-1为对称循环载荷下的疲劳强度;σm为平均应力;σu为抗拉强度。
对于载荷平均应力不为0的低周疲劳寿命预测,比较常见的是Smith-Watson-Topper(SWT)方法,其表达式为
(8)
式中:σmax为最大主应变平面上的最大拉应力。
而对于随机的变幅载荷通常使用Miner法则对疲劳寿命进行预测,其假设材料在疲劳过程中的损伤是线性累计的[48-49],按照Miner法则,N个循环造成的损伤
(9)
式中:Ni对应某一应力水平下的疲劳寿命。
但Miner法则没有考虑载荷加载的无序性问题[50],为解决此问题,学者们提出了一些不同的非线性损伤模型,比如Mesmacque等[51]将第i个水平的累计损伤定义为
(10)
式中:σedi为损伤应力,σi为第i个外载荷。
疲劳过程受力比较复杂,载荷往往是多个方向、多种形式的,对于多轴疲劳寿命,经典的预测方法有Sines准则、Crossland准则、Dang Van准则、Findley准则、SWT准则、Fatemi-Socie(FS)准则等,其中Sines准则、Crossland准则、Dang Van准则、Findley准则是基于应力的疲劳预测方法,通常应用于高周疲劳[52],而SWT准则、FS准则既能应用于高周疲劳,也能应用于低周疲劳[53]。由于疲劳损伤是个较为复杂的过程,学者们针对各自研究的具体情况,不断提出和应用新的寿命预测方法,比如Kluger[54]提出了一种基于临界平面法并考虑平均剪应力影响的多轴应力疲劳预测模型,模型损伤控制参数公式为
(11)
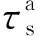
采用此模型对2017A-T4 和 6082-T6 铝合金试样在常幅值弯曲载荷、扭转载荷及两者结合的比例载荷下的疲劳寿命进行了预测,图23为2017A-T4铝合金的预测结果,可以看出不同载荷下的疲劳寿命预测值几乎全部落在了3倍分散带内。Kluger的模型不同于前人的研究之处在于,由于并不是所有材料对平均剪应力都敏感,以往的模型未考虑平均剪应力对寿命的影响[55-57]。
吴志荣等[58]借鉴FS准则和SWT准则的优点提出基于最大剪应变幅和最大剪应变幅平面上修正SWT参数的和作为疲劳损伤参数,具体公式为
(12)
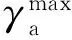
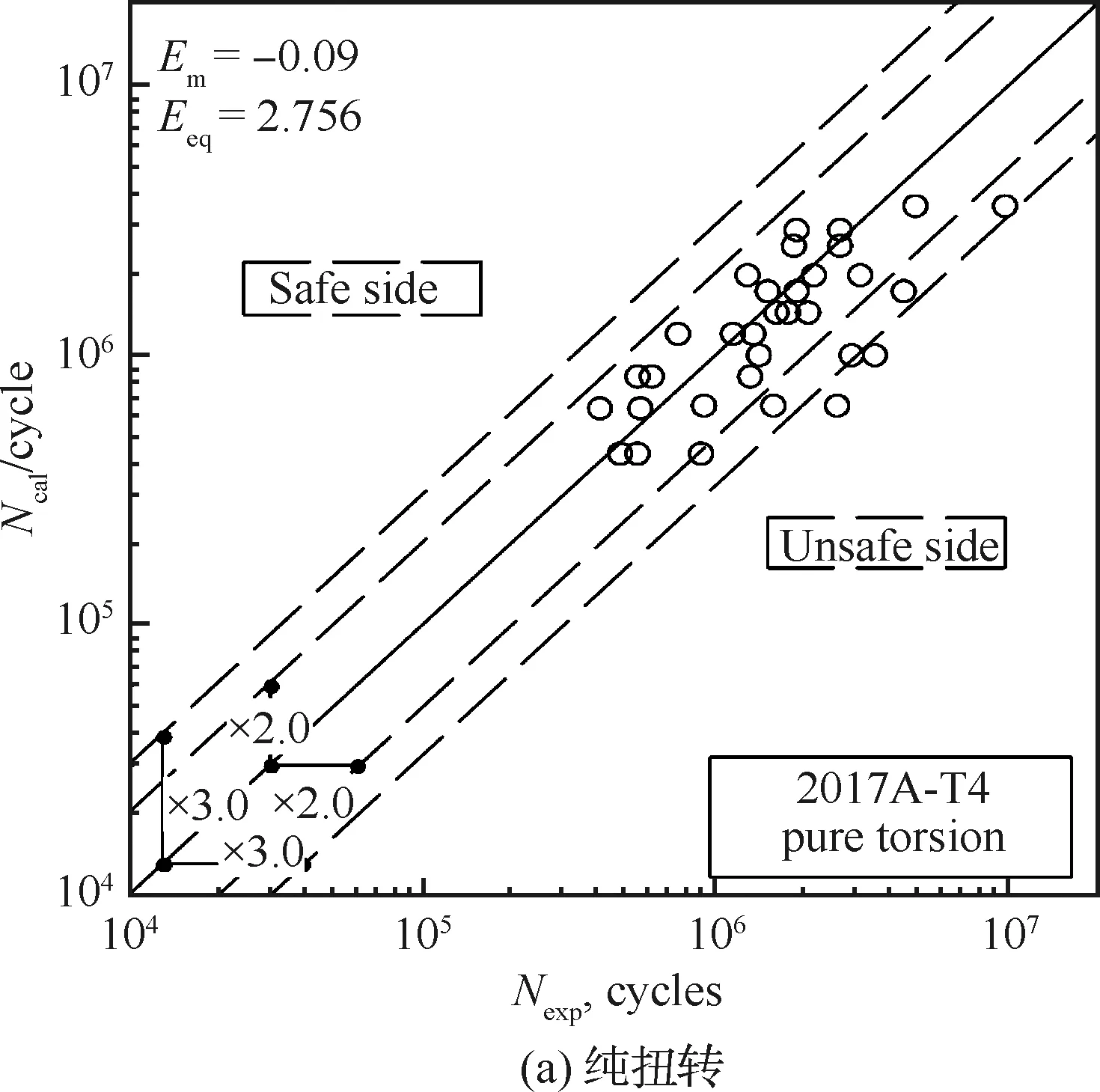
图23 不同载荷下Kluger模型预测结果[54]Fig.23 Prediction results of Kluger’s model under different loads[54]
采用纯Ti、BT9钛合金、304不锈钢等5种材料的多轴疲劳试验数据对模型进行验证,结果表明模型预测值大部分都落在2倍分散带内,图24为纯Ti和BT9钛合金的预测结果。
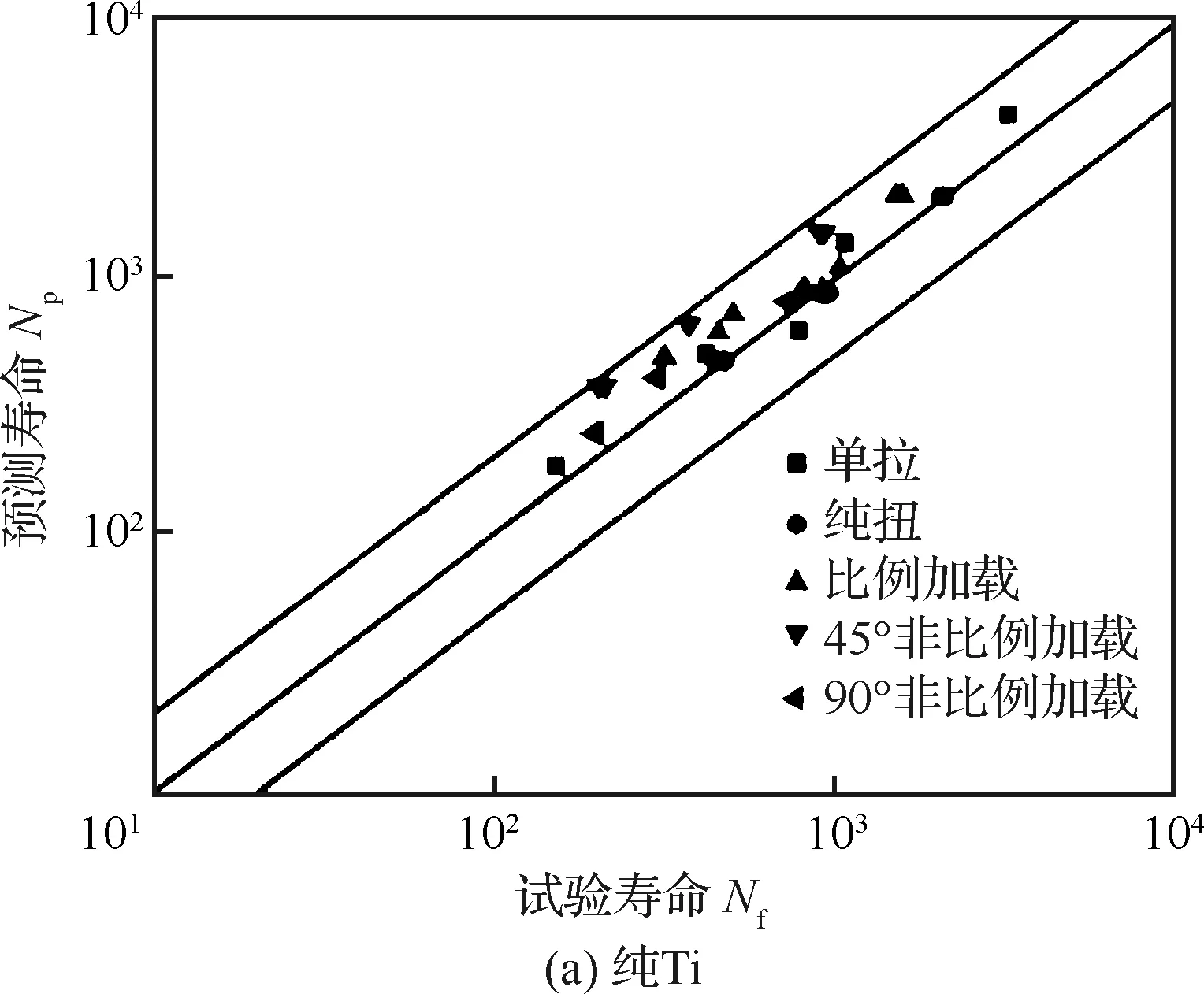
图24 吴志荣模型预测结果[58]Fig.24 Prediction results of Wu Zhirong’s model[58]
有些学者使用基于能量的方法对多轴载荷的疲劳寿命进行了预测,如Ahmadzadeh和Varvani[59]使用基于临界面能量的Varvani等3种疲劳损伤模型分别评估了变幅多轴载荷下SS304和Al7050-T7451合金的疲劳寿命,其中Varvani损伤模型具体公式为
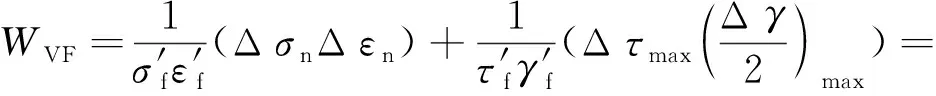
(13)
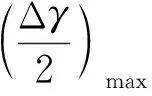
图25为3种能量模型预测结果,可以看出各模型的预测精度有所差别,但大部分的预测结果都在3倍分散带内。
还有学者针对缺口试样的疲劳寿命预测进行了研究,Wu等[60]采用基于关键距离的局部应力应变方法对TC4带缺口圆棒试样的多轴疲劳寿命进行了预测,方法原理如图26所示,点方法采用关键点的损伤参数作为疲劳寿命的计算参数,线方法采用平均值作为疲劳寿命计算的参数,所提预测模型的计算结果通过比例载荷和非比例载荷下两种缺口试样的多轴疲劳试验的验证,发现预测结果几乎都在3倍分散带内。
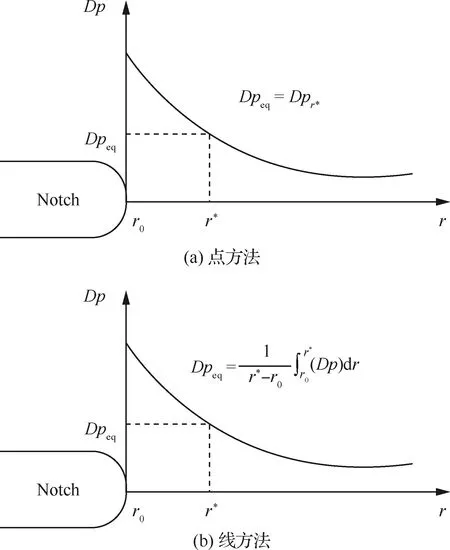
图26 关键距离方法[60]Fig.26 Critical distance method[60]
Berto等[61]使用局部应变能密度法对带V型槽的TC4圆棒试样多轴疲劳寿命进行了研究,结果如图27和图28所示,他们发现不同的应变能计算半径受载荷形式影响较大,并根据不同的载荷形式和应力比得出了相应的应变能计算公式,通过实验发现模型能够对不同载荷形式和应力比下的缺口试样疲劳寿命进行有效预测,预测结果均落在了设计的分散带内。
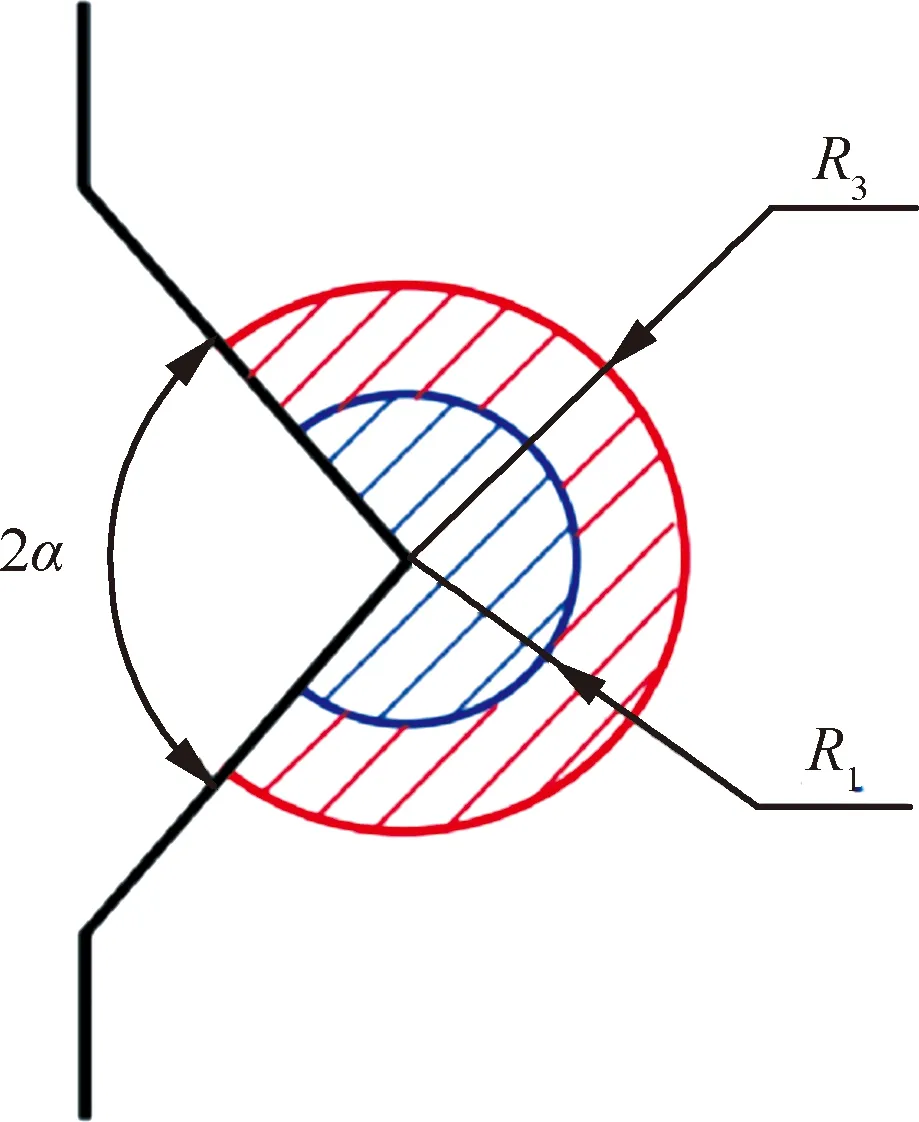
图27 不同的计算半径[61]Fig.27 Different calculation radius[61]
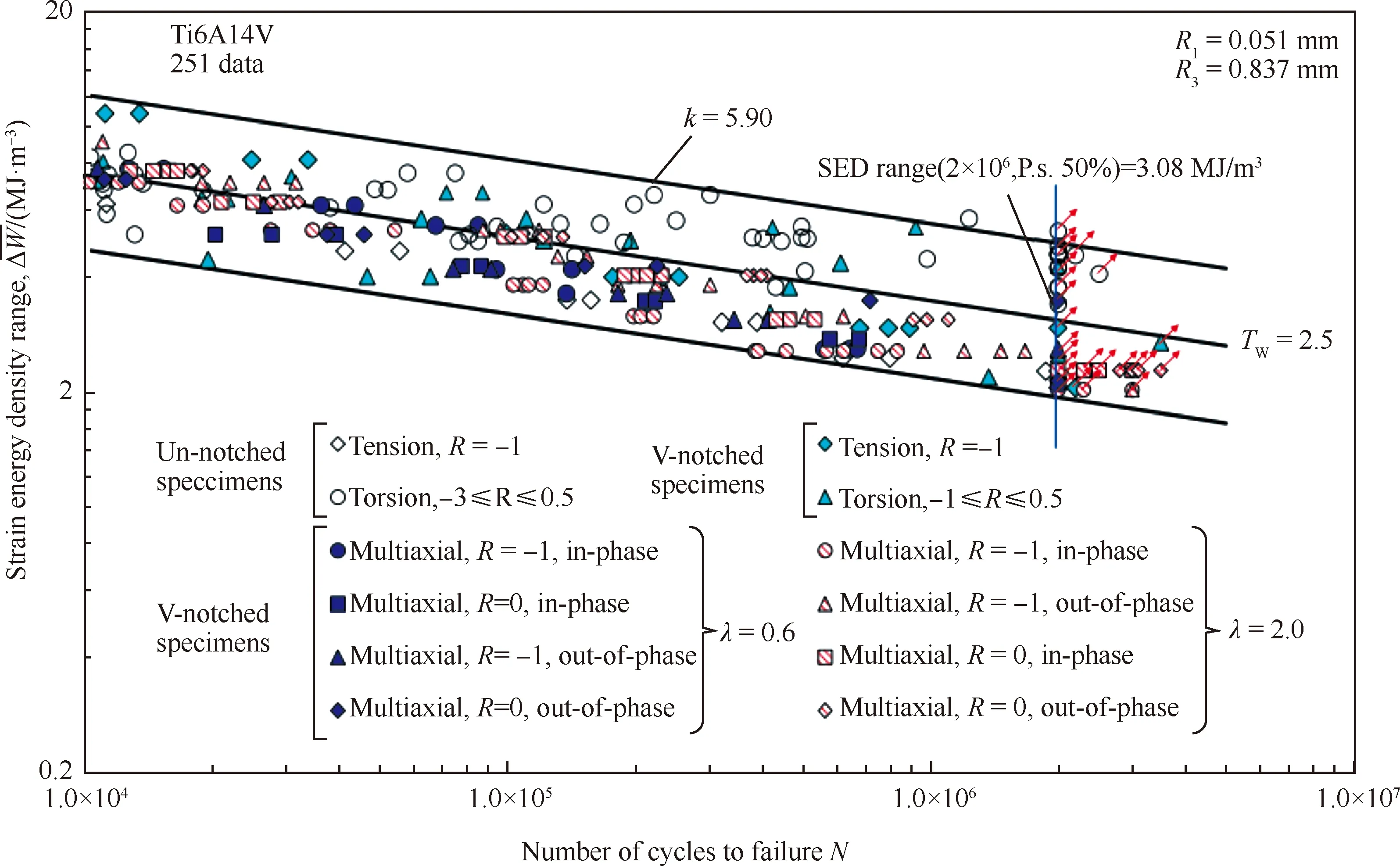
图28 应变能密度法预测结果[61]Fig.28 Prediction results of strain energy density method[61]
金丹等[62]采用有限元法和Smith-Watson-Topper法则结合的方法对非比例载荷下缺口疲劳寿命进行了预测,结果表明,大部分预测值都在2倍的分散带内。
另外,由于疲劳性能参数需要大量试验才能获得,有学者针对疲劳性能参数的获取方式进行了进一步的探索,如Shamsaei和Mckelvey[63]基于材料单向拉伸力学参数推导出了其疲劳性能参数,并使用不同的多轴疲劳模型对16种钢和高温合金比例和非比例载荷下的疲劳寿命进行预测,结果表明此疲劳计算方法是可行的,且合适的多轴预测模型的选取也十分重要。
从以上的研究发现,国内外学者提出了许多基于应力、应变或者能量等的疲劳寿命预测模型,但是很少考虑试样本身的残余应力等表面状态特征对疲劳寿命的影响,滚压强化会在零件表层产生残余应力等表面状态特征,这对零件的疲劳寿命有着十分关键的影响,因此,有必要在目前研究的理论基础上,探索一种考虑残余应力等表面状态特征的疲劳寿命预测方法。
6 总结与展望
作为表面机械强化中的一种,滚压强化具有比喷丸等工艺产生更为优异的零件表面特性,在未来的航空航天等领域的应用会越来越广泛。但是为了使零件的表面性能最优,实现零件长寿命、高可靠的目的,需要对滚压强化表面状态演化及抗疲劳机理展开深入的研究。通过对国内外表面状态特征的演化及抗疲劳机理的研究现状的总结,得出以下结论:
1) 目前对不同表面状态特征的演化研究都有了一定的基础,但是都存在一些不足之处。需要针对这些不足之处开展更为深入的研究,探究各表面状态特征的演化规律,揭示各表面状态特征的演化机理及内在联系,为表面完整性的设计提供理论依据。
2) 结合试验及有限元方法,进一步深入研究各表面状态特征及其演化与疲劳性能之间的关系,建立包含表面状态特征的适用于各种服役环境下的疲劳寿命预测模型。
3) 表面状态演化方面的理论及成果应用还比较有限,需充分挖掘其应用潜力,以军带民,扩展其应用领域和层次,提高其应用水平。

