虑及板坯几何和性能波动的薄壁件塑性成形数值模拟研究进展

崔笑蕾，詹梅,*，高鹏飞，李锐，王贤贤，雷煜东，马飞，张洪瑞

1. 西北工业大学 材料科学与工程学院 陕西省高性能精密成形技术与装备重点实验室，西安 710072 2. 陕西科技大学 机电工程学院，西安 710016 3. 中国航天科技集团公司长征机械厂，成都 610100

随着环境保护、可持续发展和节约型政策的实施，由金属塑性成形的薄壁件因容易实现轻量化、低成本、短周期制造，在航空、航天、汽车工业等高端装备领域获得日益广泛的应用[1-2]。大直径薄壁燃料贮箱箱底为代表的大型复杂异型曲面构件[3-4]，飞机机身、机翼蒙皮/壁板、复杂空心多层结构壁板，汽车行李箱盖内板零件、防撞梁和保险杠等[5-7]就是其中典型的代表。这类整体化、薄壁化、复杂化构件常采用具有轻质、高强度特性的铝(锂)合金、钛合金、高温合金等材料制造。这类构件通常采用整体薄板，通过内高压成形[8]、滚压成形[9]、冲压成形[10]、滚弯成形[11]、旋压成形[12]等塑性成形技术成形。

成形上述构件所需的大型薄壁板坯通常由轧制-热处理获得，成形中由于设备参数扰动、工装误差、模具损耗、热处理等原因，会造成板坯表面形貌参数波动、初始几何形状偏差、壁厚不均匀、微观组织不均匀、宏观材料性能波动等现象[13]。而且，针对无法直接成形的超大尺寸板坯，需要通过拼焊的方法成形，会进一步增加成形板坯的几何与性能波动特征[14-15]。大型超宽板坯/拼焊板中存在的几何和性能波动，会对后续塑性成形过程中变形行为与规律产生影响，可能会加剧变形不均匀性及产生起皱、过度减薄、开裂、厚度不均等多种成形缺陷的可能性，进而导致成形质量及成形极限下降[16-19]。而大型板坯的几何和性能波动呈现很强的分散性和随机性，定量表征和描述难度大，进一步增加了大型薄壁构件塑性成形行为研究与调控的难度[20-21]。因此，系统研究大型金属板坯的几何与性能波动特征对其塑性成形中变形行为的影响规律，掌握不确定性分析以及稳健调控方法，是实现大尺寸薄壁件高性能塑性成形制造的关键。

针对上述问题，国内外学者开展了相关研究并取得了一些进展。综述板坯几何和性能波动的表征及建模、板坯几何和性能波动对薄壁件塑性成形的影响以及虑及板坯几何和性能波动的薄壁件塑性成形不确定性分析与优化等方面的研究进展；并提出虑及几何和性能波动的薄壁件塑性成形研究中仍需研究解决的参数测量、表征精度、模型运算效率的提高，传递规律预测，优化算法的改进以及考虑多参数波动耦合作用下成形质量调控等问题。

1 板坯几何和性能波动的表征及建模

准确表征金属板坯几何和性能波动特征是建立考虑板坯几何和性能波动的大型薄壁件塑性成形有限元模型，研究其塑性成形规律与调控方法的前提。因此，开展精确的板坯几何和性能波动表征方法研究也成了近年来国内外学者关注的焦点。

1.1 几何波动表征及建模

根据板坯尺寸大小，板坯几何参数波动的数学表征及有限元建模主要步骤可归纳为两类，如表1所示。当板坯尺寸较小时，板坯的几何参数波动主要关注板坯表面形貌参数。板坯表面形貌参数由波距大于10 mm的宏观平面度、波距小于1 mm的微观粗糙度和波距介于二者间的波纹度以不同的幅值共同叠加而得[22-23]。所以，针对小尺寸板坯表面形貌波动特征，通常采用多尺度波动特征先离散分解再耦合的方法实现[24-27]：首先，对板坯表面形貌参数(平面度、波纹度以及粗糙度)进行测量并进行归一化处理，再通过离散分解法将板坯表面形貌参数的幅值分解到不同的尺度下，获得板坯表面形貌参数波动的数学函数；其次，在有限元模型中将板坯网格进行多尺度划分，分别为稀疏区域、中间区域、密集区域3种不同尺度；最后，针对不同区域的网格节点进行赋值，稀疏区域对应平面度，中间区域对应波纹度，密集区域对应粗糙度，实现多尺度参数的板坯表面形貌参数的耦合，生成满足粗糙度、波纹度和平面度叠加形状的表面形貌参数的多尺度表征，表面形貌参数及网格划分赋值区域示意图以及板坯表面形貌有限元仿真如图1及图2所示[24]。游洁[28]、王中宇[29]、陈国安[30-31]等均采用上述方法完成了板坯表面形貌参数多尺度建模与仿真。上述多尺度波动特征先离散分解再耦合的方法虽不受板坯表面复杂度的影响，但板坯表面形貌参数波动表征需要通过有限元法实现，易受板坯尺寸大小的影响，对于大尺寸板坯几何参数计算存在计算时间长、模拟过程复杂的问题；同时，节点分区域赋值的方法无法实现板坯几何参数波动的完全随机表征。

表1 板坯几何参数波动数值模拟步骤及方法

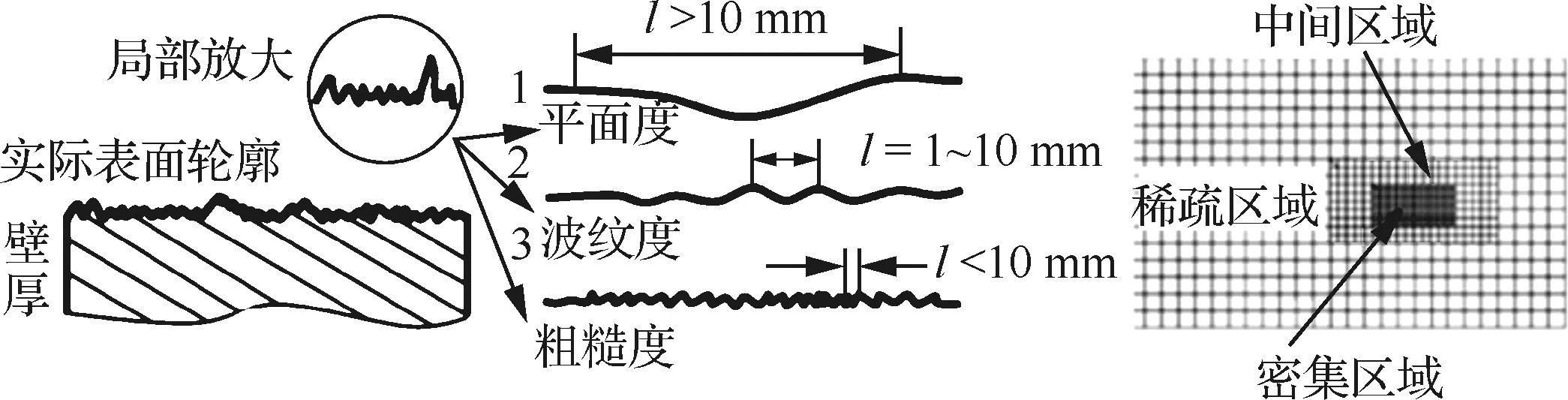
图1 表面形貌参数及网格划分赋值区域示意图[24]Fig.1 Diagram of surface topography parameters and meshing assignment region[24]

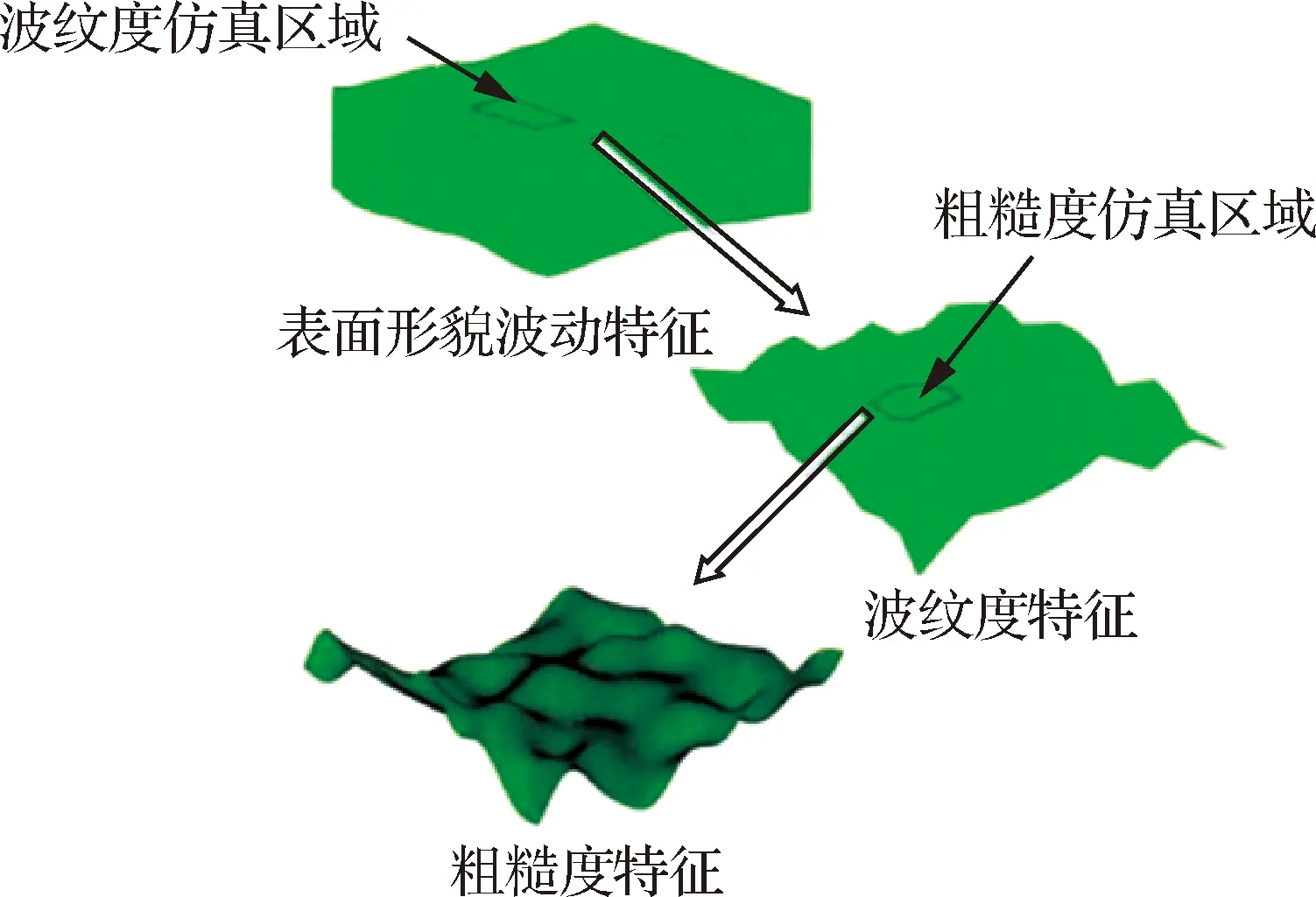
图2 表面形貌的仿真图[24]Fig.2 Simulation of surface topography[24]

Cui等[32-33]依据大型板坯实际测量的壁厚参数域，定义大型薄壁板坯壁厚3种波动类型：壁厚均值整体与基准值差别不大的基准型、壁厚均值整体超过基准值的偏厚型、壁厚均值大致小于基准值的偏薄型，以及±10%、±20%、±30% 3种壁厚波动幅度。同时，根据成形构件所需圆板在带状板坯的裁剪位置差异[34-35](平面度及壁厚波动示意图如图3所示[34])，定义板坯平面度波动类型：板坯中间2/3条带区域向下凸出型(下凸型)、板坯中间2/3条带区域向上凸出型(上凸型)、板坯两侧局部区域一上一下翘曲型(翘曲型)，其波动幅度有±0.5 mm和±1.0 mm 2种。例如壁厚偏厚型、波动幅度为±30%以及平面度上凸型、波动幅度为±1.0 mm板坯的有限元模型如图4[32]及图5[33]所示。

图3 平面度及壁厚波动示意图[34]Fig.3 Diagram of flatness and thickness fluctuation[34]

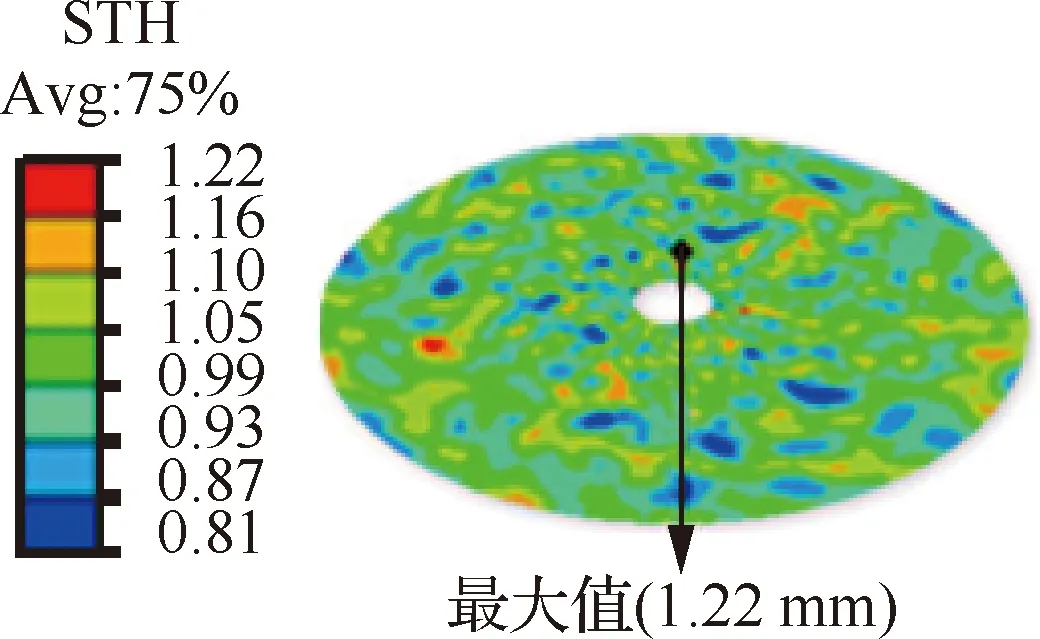
图4 板坯壁厚波动与分布[32]Fig.4 Blank thickness fluctuation and distribution[32]

Li等[36]将淬火后几何形状波动板坯平均分成25个小方块，测量每个方块中心的壁厚，确定实验板坯的厚度偏差为0.01 mm。对数据进行线性插值处理获得厚度分布，厚度分布图如图6所示，其中节点偏差坐标z(x,y)为

图5 板坯平面度波动与分布[33]Fig.5 Blank flatness fluctuation and distribution[33]

(1)

式中：z0为理想板坯表面在厚度方向坐标值；f(x,y)为壁厚测量范围内随机分布的值。

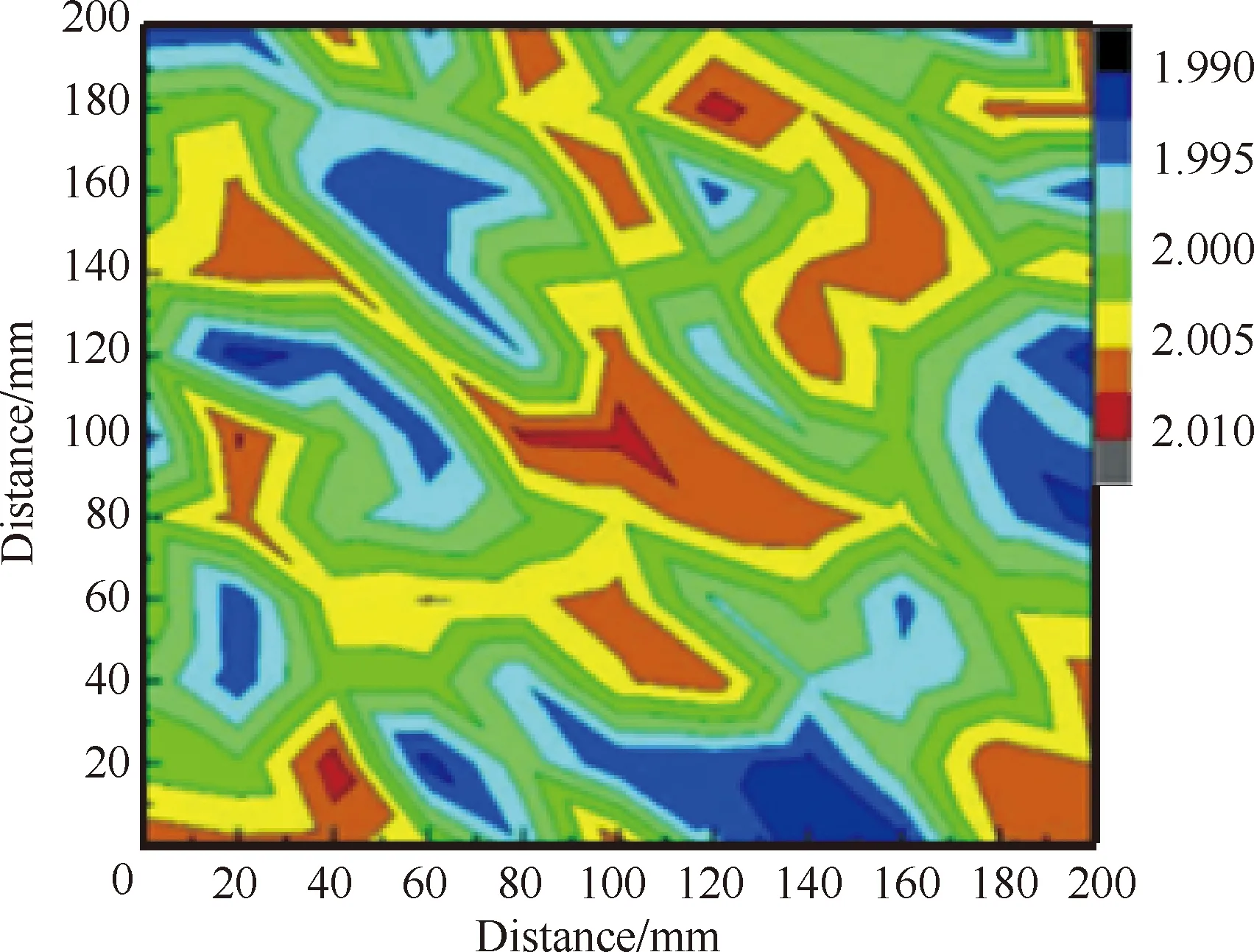
图6 初始板坯的厚度分布[36]Fig.6 Thickness distribution of initial blank[36]

1.2 性能波动特征表征及建模

材料性能是影响金属板坯塑性成形质量的关键因素，板坯在轧制以及再加工(如淬火或焊接)过程中性能(如弹性模量、屈服强度、抗拉强度以及延伸率等)会出现波动，且波动具有离散性与空间分散性[37-38]。国内外学者主要采用概率模型和分布模型来表征性能参数波动特征，并采用节点赋值[39]或子程序开发[40]方法将其耦合到有限元模型中实现板坯性能波动表征。

图7 主要素分析法流程[44]Fig.7 Process of principal component analysis[44]

Li等[46]将材料弹性模量的空间分布假设为一高斯分布的随机场，对随机场的离散采用级数最优线性估值法，即通过将随机场域离散为一系列节点a1,a2,…,an来降低计算代价，其中随机场在这些节点处的值由向量z=[y(a1,w),y(a2,w),…,y(an,w)]T表示，避免Karhunen-Loeve级数展开法[47]求解复杂的积分特征值问题。该方法能够有效实现随机变量的维度缩减，并实现材料性能波动的空间分散特征表征。

以上概率模型表征方法认为板坯材料性能参数间是独立的，并把每个分量分别用一维的概率分布进行描述，而分量之间通常不是独立的关系，表征材料属性的不均匀性波动的分布模型被提出，如Shi等[48]建立了铝合金板坯流动应力波动的分布模型，如图8所示，图中灰色区域为材料流动应力变化范围。他们将材料流动应力作为塑性应变的函数，并用一个随机的比例因子k表示，其变化量为S=k×S(ε)，其中k服从正态分布，S(ε)为应力应变初始表达式。针对金属板坯残余应力具有在板坯不同层有不同分布的特征，Zhang等[49]综合考虑铝板各部分的材料性能波动情况下，进行了铝板淬火后沿厚度方向的屈服极限性能差异对铝板进行了不同预拉伸量的仿真计算，推断出屈服极限性能的非均匀性极大地影响着预拉伸消除残余应力的效果。该方法在一定程度上提高了预拉伸后残余应力的仿真精度，但没有进一步考虑铝板弹性模量的性能差异，依然存在预测精度低、分布线形偏差大的问题。实际上弹性模量随塑性变形的变化而变化，该因素已经被证明对弯曲件的回弹量有很大影响。

图8 流动应力变化范围[48]Fig.8 Variation of material flow stress[48]

由于淬火和预拉伸过程均伴随着塑性变形，为此，秦国华等[50]将预拉伸铝板整体材料性能参数，泊松比，屈服强度，弹性模量，硬化指数分别代入相关计算公式中，获得各层的屈服极限、淬火后的弹性应变、等效淬火塑性应变及淬火后的弹性模量。根据各层的数据，通过多项式拟合可得沿厚度方向上的屈服极限曲线表征不同残余应力分布。在有限元建模中，铝板采用C3D8R单元进行网格划分，利用Static General分析步进行分析，铝板预拉伸后残余应力云图，如图9所示。针对焊接类金属板坯性能波动特征，Song等[51]和Zhan等[52]分别利用纳米压痕实验和显微硬度实验表征了热影响区内材料属性非均质性波动特征，建立了焊缝耦合细分热影响区本构模型，这类本构模型虽然考虑了热影响区内材料属性的非均质波动性，但未考虑连续变化特征。Xing等[39]利用纯板坯和焊接混合板坯试样单向拉伸试验所获的数据，基于等效混合法则，并结合接头显微硬度连续分布，建立了考虑焊缝、热影响区和母材性能连续变化的非均质材料本构，确定了如图10所示的2219铝合金拼焊板连续本构模型。

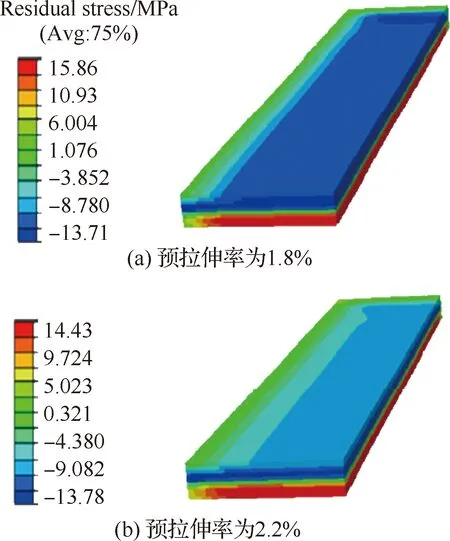
图9 预拉伸后残余应力云图[50]Fig.9 Cloud chart of residual stresses after pre-stretching[50]

图10 2219铝合金拼焊板连续本构[39]Fig.10 Continuous constitutive model of 2219 aluminum alloy welded blank[39]

2 板坯几何和性能波动对薄壁件塑性成形的影响

不可避免的板坯几何和性能波动会导致薄壁件塑性成形中出现缺陷，造成成形件质量不稳定和废品率升高。为消除或减小薄壁件塑性成形中出现的缺陷，提高成形件质量以及产品合格率，需分析板坯参数波动的影响规律。

目前，关于板坯尺寸(壁厚)、几何形状(平面度)波动对薄壁件塑性成形质量的影响规律分析较少。Cui等[32-33]基于虑及板坯尺寸、几何形状波动旋压有限元模型，分析了金属板坯壁厚、平面度波动特征对薄壁件成形质量的影响。获得了金属板坯壁厚波动对薄壁件头部、中部和口部(图11) 壁厚分布的影响规律，并给出了板坯选取指导性原则：如需将旋压件壁厚波动控制在25%范围内，建议板坯壁厚波动不超过(10%的波动，并且板坯头部尽量避免偏薄型，口部尽量避免采用偏厚型。同时，也研究了板坯平面度3种波动形式(下凸型、上凸型、翘曲型)和2种波动幅度(±0.5 mm及±1.0 mm)下旋压所得薄壁件头部、中部和口部不均匀变形程度的影响规律，发现如需将薄壁件不均匀变形程度控制在0.2 mm范围内，建议板坯平面度波动不超过±0.5 mm，并选用翘曲型板坯和中心平面度波动小的上凸型坯。

图11 薄壁成形件头部、中部和口部位置示意图[32]Fig.11 Schematic of head, middle and mouth positions of thin-walled forming part[32]

在板坯残余应力波动影响成形件质量研究方面，Abvabi等[53-54]建立了包括板坯减薄制坯和板坯轧制成形的模型，并以此研究了制坯过程引入的残余应力对轧制成形过程的影响，研究结果表明，与不考虑残余应力的模型相比，联合模型对轧制过程中形状缺陷的预测更为准确。Weiss等[55]在板坯厚度方向上设置残余应力分布，不同厚度下残余应力分布如图12所示，采用有限元法预测板坯在轧制前以及轧制壁厚减薄1.4%时材料弯曲过程中纵向应力的演化。研究发现残余应力对材料变形过程中的弹塑性转变有很大影响，并导致材料在随后的弯曲成形中趋于软化及使屈服应力降低。秦国华等[50]在考虑铝合金弹性模量变化的基础上，通过铝合金在不同拉伸率下的拉伸力学实验，获得了弹性模量-塑性变形的曲线，极大地改善了预拉伸过程的仿真模型，大幅度提高了预拉伸轧制方向残余应力的预测精度，实现预拉伸后残余应力分布曲线特征的实际趋同性。Li等[56]通过实验和有限元研究分析了考虑初始板坯参数波动的2219铝合金薄板淬火时的变形行为及成形机理。结果表明，淬火后薄板的变形形式主要有马鞍形、铲形和拱形3种形状。这些结果将为先淬火后塑性成形的多工步工艺中的变形调控提供参考。

图12 板坯减薄不同厚度时残余应力分布[55]Fig.12 Residual stress distributions for different thickness reduction[55]

在拼焊金属板对塑性成形质量影响方面，Adamus和Lacki[57]研究了由钛合金组成的拼焊板厚度变化对成形质量的影响。龚志辉等[58]研究发现在差厚拼焊板冲压过程中，忽略坯料阶梯形状会影响拼焊板冲压成形，从而影响实际焊缝线形成的位置及形状。雷新鹏[59]开展了2219铝合金拼焊板旋压成形大型薄壁异型曲面构件研究，发现构件口部壁厚薄、直径大，采用一道次拼焊板成形凸缘容易起皱，多道次强旋普旋结合成形能成功旋制出拼焊板薄壁异型曲面构件，如图13所示，①～⑤分别为旋压各道次成形后异型曲面构件大端轮廓形状示意曲线。

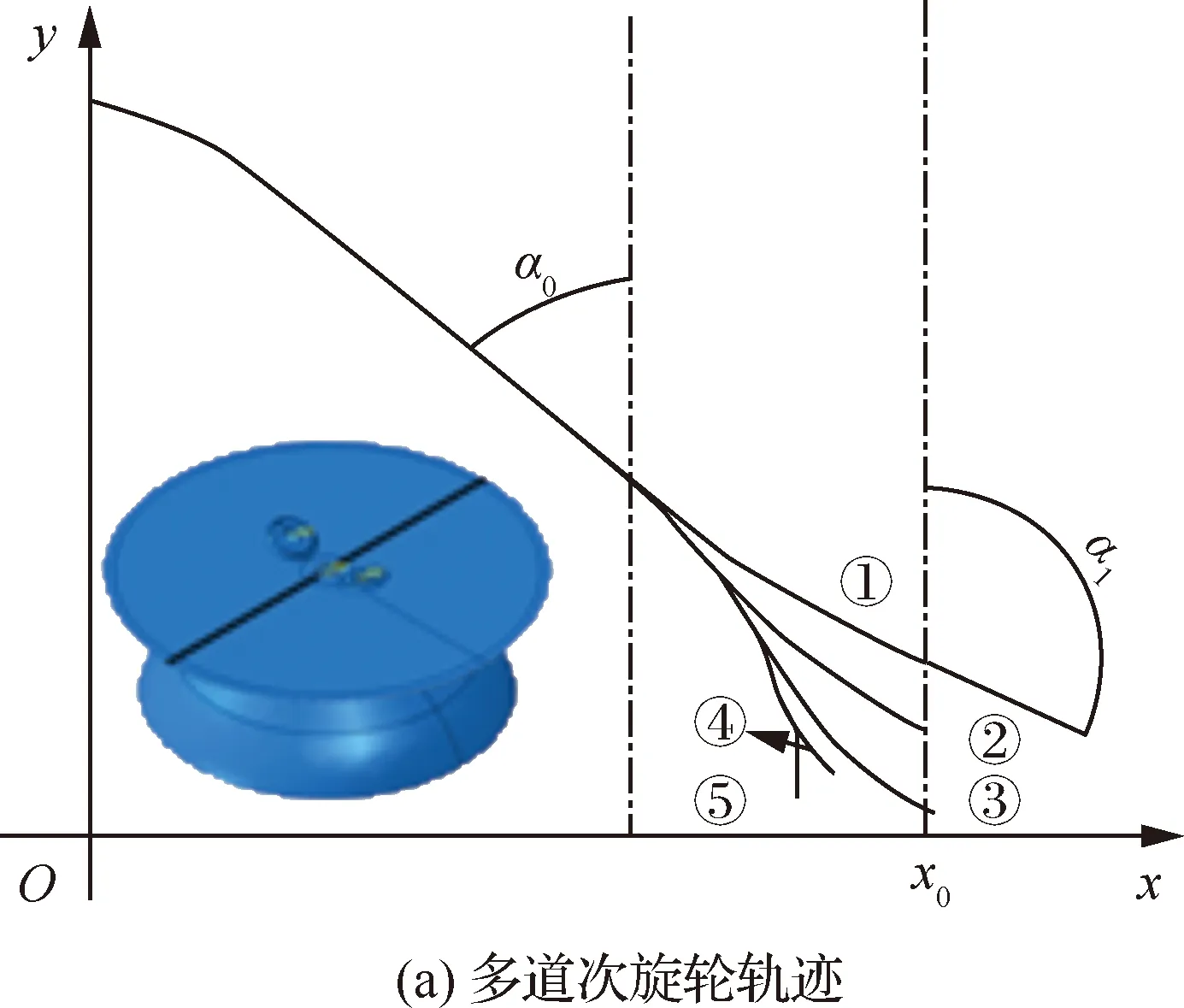
图13 拼焊板薄壁异型曲面旋压成形[59]Fig.13 Thin-wall special-shaped spinning with tailor-welded blanks[59]

3 虑及板坯几何和性能波动的薄壁件塑性成形不确定性分析与优化

为使成形件质量指标对波动因素的敏感性降至最低，获得较好的成形件质量或者合格率等规定目标，必须在工艺设计阶段将这些波动等不确定性因素纳入考虑，针对不确定性因素的研究通常采用不确定性分析以及稳健优化的方法[60]。在虑及参数波动的不确定性分析及稳健优化研究中，学者们将参数波动定义为不确定性或噪声。不确定性(噪声)参数按照来源性质可以分为三类[61-63]：随机不确定性、认知不确定性以及误差(数值不确定性)。随机不确定性以及误差来源于系统固有的偶然性，一般采用概率论和随机理论表征；认知不确定性来源于知识的不完备或缺乏相关信息，采用非概率方法，如：证据理论、模糊集、区间理论、随机集和概率盒等表征。不确定性分析方法有蒙特卡洛仿真、随机响应面法、多项式混沌展开法、基于可靠性分析的方法[64]以及Du等[65-66]提出的系统不确定性分析法和并行子系统不确定性分析法。稳健优化方法大体上可分成两类：第一类以经验或半经验设计为基础，如田口方法、响应面法、双响应面法、广义模型法等；第二类与优化技术相结合，主要有容差模型法、容差多面体法、随机模型法、灵敏度法、以及混合稳健设计等[67]。学者们综合地采用上述方法对虑及板坯几何和性能波动的薄壁件塑性成形过程进行了不确定分析与优化分析。

Kleiber等[68]以成形极限图为约束条件，利用响应面方法、可靠性理论方法分析塑性成形过程中由于摩擦、材料性能、厚度和压边力等波动的影响下，成形过程中板坯失效的概率。Zhang等[69]将响应面法与概率设计相结合，以零件的拉深成形为例，将材料参数视为不确定性因素，在给定坯料形状和模具的条件下，利用概率设计的

方法获得了最佳的压边力和摩擦系数组合。张骥超等[70]为了得到随机因子发生波动时对产品成形质量的影响，以侧围外板冲压成形过程为例，结合有限元模拟仿真技术、试验设计方法、响应面模型法，获得了在材料参数不发生波动的情况下的最优工艺参数；并同时通过蒙特卡洛模拟法分析了质量评价指标的均值与标准差，最后通过6σ(σ水平值大小是用来评价产品特性好坏的综合性标准，其数学意义为标准差，可用来衡量百万件产品的不良率)稳健优化方法获得了稳健性最好的工艺参数。孙光永等[71]等提出了构造双响应面模型的思想，分别建立了产品特性的均值与标准差的响应面代理模型；以及约束的均值和方差的响应面代理模型；在构造出代理模型的基础之上，结合6σ质量管理思想和建立的双响应面代理模型，构造了基于σ质量管理的板坯成形质量多目标稳健优化模型。稳健优化结果表明板坯成形质量的稳健性得到了显著性的提高。Lafon等[72]针对DP780钢U形板拉深，考虑材料性能屈服强度，抗拉强度以及壁厚的波动性，采用蒙特卡洛响应面建立波动参数与成形指标间模型，采用随机优化算法获得稳健优化问题的解(帕累托前沿)，优化结果表明通过控制成形工艺参数压边力可以减小U形板的回弹效应，减小板坯参数及工艺参数波动的影响。上述采用多项式响应面模型表达形式直观、操作方便，但若参数较多，采用多项式响应面时，响应面方程较为复杂，反而降低预测精度。

由于响应面法作为代理模型时对多参数问题预测精度低的局限性，有些学者引入了Kriging代理模型方法，该模型在描述非线性程度较高的问题中具有更好的预测效果[73]。黎凯等[41]在金属板坯冲压稳健优化过程中，考虑材料性能波动的情况，采用Kriging方法[74]建立拉裂、起皱及平均减薄率与设计参数之间的代理模型。以拉裂、起皱为基础的约束条件，以平均减薄率为基础的优化目标，通过蒙特卡罗模拟法分析不确定性因素下平均减薄率的均值和方差，采用遗传算法对问题进行求解，结果表明考虑材料性能波动以及代理模型波动的稳健设计方法能有效地降低拉裂、起皱约束失效概率，提高冲压件成形质量和工艺稳健性。李方义等[75]将拉深成形中的摩擦因数作为波动参数，采用非线性区间数值规划对其进行描述，以厚度不均程度最小和起皱最小为目标函数，采用Kriging近化模型提高优化效率，基于多目标遗传算法和序列二次规划算法的混合优化算法获得了压边力和拉深筋阻力的Pareto最优解。胡静等[76]针对板坯拉深成形工艺中设计变量波动的影响，将稳健设计与板坯塑性成形有限元仿真、代理模型相结合，提出了基于Dual-Kriging模型的稳健设计方法，并将其运用到盒形件的压边力、凸模半径、摩擦系数稳健设计中，提高了方盒件成形质量的稳健性。谢延敏[77]为减少冲压成形过程中波动因素引起的成形质量波动，同时克服传统的静态代理模型方法全局近似精度低的问题，提出基于动态Kriging 模型的冲压成形工艺稳健设计方法，该方法可以对模型进行优化时采用全局优化自动搜索算法进行求解，不断通过试验设计方法对样本和代理模型进行更新提高代理模型的精度。优化结果表明，将动态Kriging模型与稳健设计方法结合应用到板坯冲压成形中，对零件的最终质量有较好的控制效果。

采用最短距离法评估不确定性及稳健性方面，Shi等[48]提出了一种结合有限元法的不确定性分析和工艺优化方法，并在金属旋压工艺中得到了应用。在对材料流动应力、板坯壁厚和旋轮进给率3个随机波动变量进行概率建模的基础上，采用蒙特卡罗响应面法和拉丁超立方抽样构造响应指标(成形件最小厚度和总旋轮力)与波动参数间代理方程即响应面。进一步采用最短距离法[78]来研究响应指标的概率分布对系统评估分析，以研究响应超出所需边界时的故障概率，采用控制变量法[79]对工艺响应进行优化以符合3σ质量要求。Rahman和Wei[80]提出了一种利用最可能点作为参考点的单变量方法来近似多元函数，以预测结构和机械系统在随机载荷、材料性能和几何形状变化下的失效概率。但是最短距离法正态化时在设计点累积函数和密度函数当量转换时的误差较大[81]。

为进一步减小代理模型误差以及获得更稳健的可靠解，众多其他不确定性分析及稳健优化方法被提出，如Sahai等[82]以回弹最小为目标，板坯厚度、模具间隙、弹性模量及屈服强度为不确定性因素，应用序列优化及可靠性评估法对翻边工艺进行了参数优化。汤禹成和陈军[83]针对高强度钢板拉伸成形中存在的噪声因素，提出了基于支持向量机和重要度抽样的板坯成形工艺稳健设计方法，结合优化算法求解既满足质量可靠性又保证质量目标的最佳成形工艺参数。Jiang等[84]将摩擦系数作为U形件拉深成形过程中的不确定因素，回弹量作为目标函数，基于非概率不确定优化方法，获得了优化的台阶型变压边力曲线。田少许[60]提出了一种基于序列近似的薄板拉深成形变压边力设计方法。变压边力为设计变量，薄板拉深成形质量评价指标为目标函数和约束，构建了薄板拉深成形变压边力为多目标优化模型，基于多宽度RBF神经网络和序列采样策略建立了关于目标函数和约束的序列近似模型，在此基础上，采用遗传算法对薄板深拉深成形变压边力设计问题进行优化求解。这些不确定性分析及稳健优化方法的计算精度得到了提高, 但精度的提高往往以牺牲计算效率为代价，需针对工程设计选择合适的不确定性分析与稳健设计的方法。

4 结论与展望

用于塑性成形的大型金属板坯存在不可避免的几何以及性能波动显著增加复杂薄壁件塑性成形中变形的复杂性，导致成形质量及成形极限下降，极大制约了大型薄壁件的精确成形。从板坯几何和性能波动的表征及建模、板坯几何和性能波动对薄壁件塑性成形的影响以及虑及板坯几何和性能波动的薄壁件塑性成形不确定性分析与优化等等方面综述了相关研究进展。同时，基于这些方面，考虑未来可能的研究方向有：

1) 金属板坯几何及性能波动参数测量、多尺度表征方法及建模

金属板坯成形前要经历铸造、改锻、轧制、挤压、拉拔或卷焊等多个工序和道次的复杂热力加载制备过程，设备工艺参数扰动、工装误差、模具损耗等产生的加工公差，往往不可避免导致板坯出现几何及性能参数波动、微观组织波动等现象。为建立精准模型并指导薄壁件精确成形，需要进一步优化波动参数测量技术，探究板坯几何和性能波动特征以及微观组织波动耦合的全尺度表征新方法；同时，基于参数波动特征表征，建立高效精确的全尺度参数波动的薄壁件塑性成形有限元模型。

2) 金属薄壁件塑性成形过程中参数波动因素测量及耦合作用分析

金属薄壁件塑性成形过程中波动的因素多，测量难，且具有时变的特征。目前多数研究仅考虑板坯几何及性能等少数成形参数的不确定性并假设参数的波动为正态分布，但是实际成形过程中，模具参数、工艺参数、摩擦接触状态下多场加载条件以及环境温度也会出现波动，且波动概率分布函数可能是非正态分布。因此，需要结合实验测量方法、概率统计、随机模拟或模糊理论等，深入系统研究初始板坯、成形过程和环境参数等物理性波动的测量及其耦合作用规律。

3) 金属薄壁件成形过程中不确定波动传递规律和预测

金属薄壁件成形是多重非线性过程，不确定性因素贯穿整个成形过程，如初始板坯几何及性能波动的不确定性，成形过程中成形参数波动的不确定性；对成形过程进行不确定性分析及优化过程中的统计模型样本容量带来的波动、建立的有限元模型自身数值计算波动、以及参数与成形质量间代理模型波动等的不确定性。上述不确定性因素如何传递，对成形过程及成形件质量及精度的影响也尚未得到重视。因此，需要结合实验设计、精确抽样方法、智能优化以及专业质量预测系统等，深入研究复杂薄壁金属件塑性成形过程中不确定性波动传递规律和预测。

4) 虑及参数波动的不确定性或稳健性的多参数多目标多约束优化设计算法和方法

各国学者相继提出通过主成分分析法、敏感性分析法、试验设计对成形参数进行影响程度分析的同时采用回归模型、响应面分析法、支持向量机、神经网络方法分析建立成形参数与成形质量指标间的代理模型并分析其的影响；同时在大数据和计算机高速发展的影响下，优化方法也将更大程度地依赖于机器学习以及仿真算法等，如蚁群算法、模拟退火法等已经应用于过程系统的优化过程中。但是金属薄壁件成形过程设计是多参数多目标多约束的非线性优化设计问题，并且塑性变形具有时变性和复杂性特征，因此，如何提高代理模型的预测精度并发展基于不确定性或稳健性分析的高效可靠性和稳健性优化算法，是虑及参数波动塑性成形中仍需探索的方向。

5) 虑及参数不确定性波动的金属薄壁件精密塑性成形质量控制

成形参数不确定性波动将导致成形过程中变形状态表现出时变特征，进而积累影响整体成形过程，发展在线检测与动态调控方法以实时调控成形状态，控制成形质量是未来发展趋势。即，开发虑及参数波动的金属薄壁件精密塑性成形特征实时测量与表征系统，该系统可以实时感知成形状态，并将其数据化处理存储；建立成形条件与成形状态间关系模型，并基于预期成形质量综合评价指标，采用优化算法获取与参数波动匹配的工艺方案及规程；将匹配方案及规程发送到制造执行系统，并按之组织生产，实现在线检测与动态调控的成形成性一体化制造。