微纳米压痕测试技术：发展与应用

王赵鑫，赵宏伟

吉林大学 机械与航空航天工程学院，长春 130025

随着国家对航空航天及武器装备持续关注，推动着军工自主化，然而仍面临诸如航空发动机、新型材料及高端智能电子元器件等技术瓶颈。材料是一切高新技术的支撑和先导，由于航天器核心零部件往往服役于复杂苛刻加载工况下，例如被誉为“现代工业皇冠上的明珠”的航空发动机涡轮叶片、万米高空飞行的民用航空器、高超声速飞行器及可重复使用飞行器等，因此针对复杂零件材料力学性能测试技术的需求更为迫切，特别是提高接近材料真实服役条件下材料的微观变形损伤机制和性能演变规律的测试能力，是提升核心零件性能稳定性和使用寿命的关键。

传统材料力学性能测试技术通常仅能给出材料宏观力学参量，对复杂载荷条件下材料微观力学行为、服役性能(力、热和电磁等)演化规律及其与组织结构演变间的相关性规律、交互作用机制就很难给出定量解释，因此针对微小尺度材料测试技术应运而生，例如选择微区利用聚焦离子束(FIB)去除材料制备微柱/微梁进行均匀应力/应变加载试验。然而，该技术需要破坏性样品制备、严格的测试条件和大量的操作时间，这使得该技术推广仍存在很大壁垒。另外一种有潜在应用前景的测试技术是微纳米压痕测试方法。

本文着重针对微纳米压痕测试技术的发展与应用进行概述和总结。首先对微纳米压痕测试技术发展历程简要回顾，接下来对微纳米压痕测试系统、经典数据分析方法以及纳米压痕测试技术固有存在的尺度/尺寸效应进行介绍。进而为发展多场耦合环境下微纳米压痕测试表征技术，简要描述典型磁电弹性材料在力-电-热-磁多场耦合环境下接触力学行为的解析模型。重点对目前一些在航空航天领域的应用与机遇进行分析，比如评估材料在高/低温加载环境和电/磁场耦合加载环境下的性能演化规律。旨在促进对微纳米压痕测试技术潜在发展机遇的理解，并对其所面临的问题和挑战进行概要总结。

1 微纳米压痕测试技术的发展

一个多世纪以来，压入测试技术一直是表征各种材料力学性能最常用的方法之一[1-3]。最早可追溯至20世纪初提出的定量硬度测试方法[1]，传统的压入测试技术是利用已知几何形状的硬压头以预设的压入深度或者载荷作用到较软的样品表面，通过测量残余压痕的尺寸计算相关的硬度指数，也就是众所周知的显微硬度测试技术。

随着高分辨力测试设备的出现使连续控制和监测整个压入过程的载荷和位移变化成为可能，仪器化压入测试技术(也称为深度-传感压入测试技术)应运而生[4]。相较于显微硬度测试技术，仪器化压入测试技术所能够表征的材料力学参量不再局限于硬度和弹性模量这2个基本的参量，同时也涵盖了材料屈服强度[3,5-7]、加工硬化指数[7-9]、断裂韧性[10-11]、蠕变/应力松弛[12]以及残余应力[13-15]等。极为简便的样品制备过程、无损伤的作用区域也有利于满足高通量的小尺度材料测试需求，比如薄膜/涂层、纤维等[16-17]。

近年来，应用于航空航天等领域的新型材料正在向低维化、功能化与复合化方向飞速发展，在微/纳米尺度作用区域上开展微纳米压痕测试已被广泛用作评价材料因微观结构变化而诱发力学性能变化以及获得材料物性转变等新现象、新规律的重要工具。然而，为了更好地揭示材料工程性能和变形行为，单纯依靠仪器测试精度的不断提高显然是不够的。接近服役环境下的微纳米压痕测试系统更具有应用潜力，并为多维环境空间材料性能的新发现提供了可能性[18]。此外，结合原位(InSitu)表征手段的微纳米压痕测试系统为揭示材料微区变形损伤机制提供技术支撑，甚至能够辅助构造一种理想的加载环境，比如扫描电子显微镜(SEM)腔室的高真空度可以有效避免材料高温下的氧化行为、低温下的结冰现象等。

2 微纳米压痕方法

根据不同行程的加载单元匹配不同量程、精度的检测单元，如表1[19]所示，微纳米压痕测试系统可以划分为宏观、微观以及纳观3种不同的表征范畴[19]。本节首先将根据驱动原理的不同介绍微纳米压痕测试仪器的工作原理及系统组成；其次基于压入载荷-深度(P-h)曲线阐述经典的试验数据分析方法，包括Oliver-Pharr模型、Cheng-Cheng方法以及有限元(FE)反求法；最后对微纳米压痕测试技术固有存在的尺度效应及尺寸效应进行讨论。

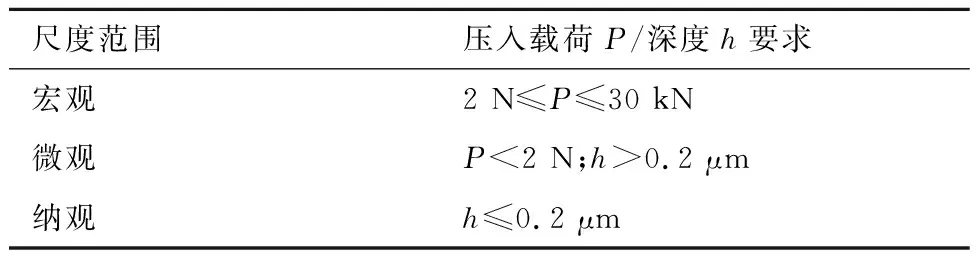
表1 微纳米压痕测试系统表征范围[19]

2.1 微纳米压痕测试系统

目前，基于不同的驱动原理所研制的商业化压痕测试系统已日趋成熟，部分商业化压痕测试系统驱动加载方案及产品优势特点情况如表2所示，然而不可否认国内尚缺乏同类商业化测试系统。图1所示为适用于不同尺度范畴的典型微纳米压痕测试系统，不难发现静电力驱动、电磁驱动以及压电驱动已成为目前纳米压痕测试系统最常用的驱动模式[20]。

表2 国外商业化压痕测试系统驱动加载方案及优势Table 2 Actuators and advantages of foreign commercial indentation testing systems

如图1所示，其中一种在商业化纳米压痕测试仪器应用广泛的驱动方式是依靠电磁加载线圈(即音圈电机)，通过支撑弹簧限制压杆在水平方向上的移动。理论上压头输出载荷与线圈输入电流成正比，并可以通过无限细分电流的方法以达到提高载荷加载分辨力的目的。然而，实际上却很难做到这一点，因为存在楞次定律引起的电气相互作用，对线圈进行精确控制是很困难的[20]。

图1 不同驱动原理的仪器化压入测试系统载荷-位移加载能力关系图Fig.1 Diagram of load-displacement relationship of instrumented indentation testing system with different driving principles

另外一种施加载荷的方法是利用静动极板间静电引力作用，不可否认这是目前载荷分辨力最高的驱动方法，最高可达1 nN(载荷噪声水平低于20 nN)。特别是在2018年，德克萨斯A&M大学微摩擦学实验室与美国Hysitron公司(现德国Bruker-Hysitron公司)合作，在商业化纳米压痕仪器的基础上引入多级梳齿极板结构，将压入载荷以及压入位移灵敏度提高了近20倍，进一步提高静电力驱动的分辨力[21]。然而，遗憾的是由于无法实现超过30 mN以上的载荷输出，限制了其在高载荷水平的应用[20]。

相比于难以控制的电磁驱动和高载荷水平的限制，基于逆压电效应的压电驱动原理更适合于小型仪器化纳米压入测试系统以及自行搭建实验平台的研究人员，如图1及图2(a)所示澳大利亚Fischer-Cripps实验室有限公司的IBIS系列仪器采用2级独立的LVDT传感器分别实时记录压入载荷和压入深度，并可独立构成闭环控制系统[20, 22]。该产品的最大特点在于其压入载荷数据不再源于软件模拟计算结果，而是载荷LVDT传感器实测值。图2(b)是瑞士Alennis公司标准款纳米压痕测试仪器[23]，它由集成有位移传感器的闭环压电促动器驱动，最大压入载荷为500 mN，最大压入位移为40 μm；图2(c)是由吉林大学赵宏伟教授团队自主研制的可集成在SEM腔室内的微纳米压痕测试仪器[24]。

图2 基于压电驱动原理的典型纳米压痕测试仪器Fig.2 Representative nanoindentation testing devices based on piezoelectric driving principle

除了上述驱动原理不同的加载单元以外，微纳米压痕测试系统通常还包括以下几个组成部分[20, 25]：

1) 检测单元：用于实时记录压头位移的变化量的高精度传感器(电容式或者电感式)。通常压入载荷由已知刚度的支撑弹簧的变形间接通过软件模拟获取；另外也有一部分测试系统采用独立检测策略直接提取压入载荷变化量(比如应变计式测力单元、静电梳齿结构的微力传感器)。

2) 位移调节单元：一个用于保证压头与测试样品表面作用区域的位置关系的二轴或三轴运动平台(不局限于伺服电机驱动平台)。

3) 压头：在压入过程中使测试样品表面产生残余压痕的工具头。根据不同的测试目的以及加载环境，需要选用特定形状(玻氏、维氏、立方角、球头、平头等)、不同材料物性(金刚石、蓝宝石、碳化钨等)的压头，特别应注意的是不同几何形状的压头适用的数据分析方法也有所区别。

4) 控制单元：用于实时高速采集、记录压入载荷/位移信号，并能够输出压入历程控制指令的计算机，同时在压入过程结束后能够对所记录的数据分析处理。

5) 观测单元：用于对压入测试前后作用区域的成像，通常采用安装不同放大倍数物镜的砖塔光学成像系统离位成像，或者利用纳米压痕压头原位扫描成像(比如Bruker TI 950)。后者的成像分辨力显然更高，但是对压头磨损程度也可能更为显著。

6) 其他附加单元：为适应不同材料的测试需求的其他组成部分，比如动态测试单元、温度加载单元以及氛围环境加载单元等。

2.2 压入载荷-深度曲线分析方法

区别于显微硬度测试技术直接观测残余压痕尺寸的方法，微纳米压痕测试技术是基于图3(a)所示的P-h曲线建立相应数学模型而后求解材料力学性能参数的方法[4]，图中，he为弹性恢复深度。

2.2.1 Oliver-Pharr模型

在过去30多年里，研究人员提出了多种不同的数学模型，其中应用最为广泛的数学模型是针对P-h曲线卸载段Doerner和Nix[26]提出的线性拟合模型以及Oliver和Pharr[27-28]提出的指数函数拟合模型。大量的试验数据表明P-h曲线卸载段的压入载荷与压入深度近似满足：

P=α(h-hf)m

(1)

式中：α为拟合系数；m为拟合指数；hf为完全卸载后的残余压痕深度。根据接触刚度(S)的定义，S可由P-h曲线卸载段顶端斜率dP/dh确定：

(2)

式中：hmax为最大压入深度。

图3 典型P-h曲线及其压痕形貌示意图Fig.3 Representative P-h curve and schematic of indentation profile

对于纳米压测试而言玻氏压头的应用最为广泛，由于其具有几何自相似特性，因此可以等效为锥形压头，在最大压入位置及完全卸载状态的纳米压痕剖面图如图3(b)所示,θ为等效锥形压头半锥角。根据式(3)计算出最大压入位置下的压头与试件的接触深度(hc)，进而可以推导出理想几何形状压头的接触面积(A)函数表达式：

(3)

(4)

式中：Pmax为最大压入位置的压入载荷；hs为压痕区域附近的弹性变形深度；ω为与压头几何形状有关的常数；ξ为投影面积系数(对于玻氏压头，ω=0.75，ξ=24.56)；a为最大压入位置的接触半径。此时根据式(5)和式(6)可以直接计算出测试材料的压入硬度(H)和压入折合模量(Er)：

(5)

(6)

式中：β为与压头几何形状有关的常数(对于玻氏压头，β=1.034)。当已知压头材料的弹性模量(Ei)和泊松比(υi)时(对于金刚石压头，Ei=1 140 GPa，υi=0.07)，测试样品的弹性模量(E)可以由式(7)计算出来：

(7)

式中：υ为测试样品的泊松比，一般取0.1～0.5之间。

尽管Oliver-Pharr模型通常能够给研究人员带来测试样品满意的弹性模量和硬度的解，但是不要忽略以下几个假设[27-28]：① 各向同性材料；② 半无限大、弹性半空间；③ 材料在加载阶段的变形为弹塑性变形，在卸载阶段仅有弹性变形回复；④ 刚性压头周围的材料仅发生凹陷变形；⑥ 不 考虑蠕变、黏弹性等与时间有关的变形。因此，为了提高Oliver-Pharr模型的普适性，针对特定试验条件的修正模型层出不穷，比如基于量纲分析解决材料发生凸起(Piling Up)变形的情况(Cheng-Cheng方法)[29-30]，薄膜基底对薄膜纳米压痕力学性能测试影响程度的修正[26,31-33]等。下面将详细阐述基于量纲分析和有限元仿真的Cheng-Cheng方法。

2.2.2 Cheng-Cheng方法

考虑用刚性等效锥形压头表征材料弹塑性行为，材料力学性能可以从单轴应力-应变(σ-ε)曲线提取：

(8)

式中：ε为应变；σ为应力；n为加工硬化指数；σy为测试样品的屈服强度。系数K等价于

(9)

式中：当n=0时，材料简化为理想弹塑性。

如图3所示，在P-h曲线加载段，压入载荷(Pl)和hc可以用材料弹塑性参量(E、σy、n和υ)、压头参量(θ)和压入深度(h)表示

Pl=f(E,σy,n,υ,θ,h)

(10)

hc=g(E,σy,n,υ,θ,h)

(11)

选取E和h为独立参量，基于量纲分析和Π定理，式(10)和式(11)可以写成

(12)

(13)

同理，在P-h曲线卸载段，压入载荷(Pu)可以表示为

(14)

对P-h曲线卸载段初始位置求导，S表达式为

(15)

而残余压痕的深度hr可由式(15)在完全卸载(即Pu=0)时获得,即

(16)

进而分别对P-h曲线加载段及卸载段积分求解压入总功(Wt)和卸载功(Wu)，其表达式为

(17)

(18)

则在压入过程中不可逆功(Wp)与Wt的比值与hmax无关，且Cheng Y T和Cheng C M[29]发现压入硬度与弹性模量之间存在如下关系：

(19)

式中：E可由式(7)推导计算而来。H/Er可用来间接反映材料的耐磨性和断裂韧性的强弱。

针对大量弹塑性材料微纳米压痕测试试验，如图4[34]所示，研究表明H/Er与Wu/Wt呈现线性关系，其中拟合程度(R)达到0.986 9。无需计算真实的接触深度，就能直接获得材料弹性模量和硬度参数。

图4 H/Er和Wu/Wt之间的关系 (用虚线线性拟合)[34]Fig.4 Relationship between H/Er and Wu/Wt with fitting line (dash curve)[34]

表3将简要对比经典Oliver-Pharr模型和Cheng-Cheng方法分析处理压痕数据的特点。

表3 经典Oliver-Pharr模型和Cheng-Cheng方法对比

2.2.3 有限元(FE)反求法

利用有限元模拟进行正反向分析是从压痕数据中提取材料特性的另一种方法。通常首先需要建立有限于模型并予以验证，判断其收敛性；其次代入特定参数运行模型，结合反向分析或者迭代算法得到压痕响应；最后参考压痕数据(试验中获取)，通过找到收敛的有限元模拟压痕响应，迭代提取材料的性能。该方法可以更方便地针对不同形状的压头及本构关系的材料提取压痕响应行为，但是不可避免地初始值的设定将对算法迭代次数及收敛性产生极大的影响。

然而，对于纳米薄膜等不便于试验的材料，数值模拟可能是一种很有潜力的提取材料压痕响应的方法。比如Yang等[35]基于有限元反求法评价SiCN涂层的弹塑性行为；Gupta等[36]结合纳米压痕试验和有限元方法首次提取氧化铟锡(ITO)透明导电薄膜材料的弹塑性特征。

2.3 压痕尺度/尺寸效应

众所周知，在不同尺度下即使对均质材料进行压痕测试，所提取的压入硬度值也存在显著区别，直观表现为“越小越硬”，这都归因于压痕尺度效应[37]。

压痕尺度效应包括材料固有尺度和外部试验尺度，其中材料的固有尺度取决于其微观结构特征(比如样品尺寸、晶粒/亚晶尺寸以及析出物间距等)的大小；外部试验尺度将直接由特定的压入条件引起，即著名的压痕尺寸效应(ISE)[38]。一方面如图5(a)所示，利用玻氏压头或者其他锋利压头压入不同晶粒及晶界位置，研究不同晶体取向及晶界对变形行为及力学参量的影响。另外，对于低维材料，比如薄膜、涂层及其他微小器件等，仅适合于纳米尺度压痕测试。如图5(b)所示，微米尺度压痕测试对表征多晶材料组成相的力学性能更为适用，也用于表征材料表面硬度及组成相力学差异。而宏观尺度压入测试可以忽略样品局部区域的不均匀性，并获得材料平均硬度值(HM)。结合大量压入试验结果，统计分析可得多晶材料宏观-微观硬度关系或者微观-纳观硬度关系，如西北工业大学的Wang等[39]分析多道次流动成形TA15合金不同微观组成相对材料宏

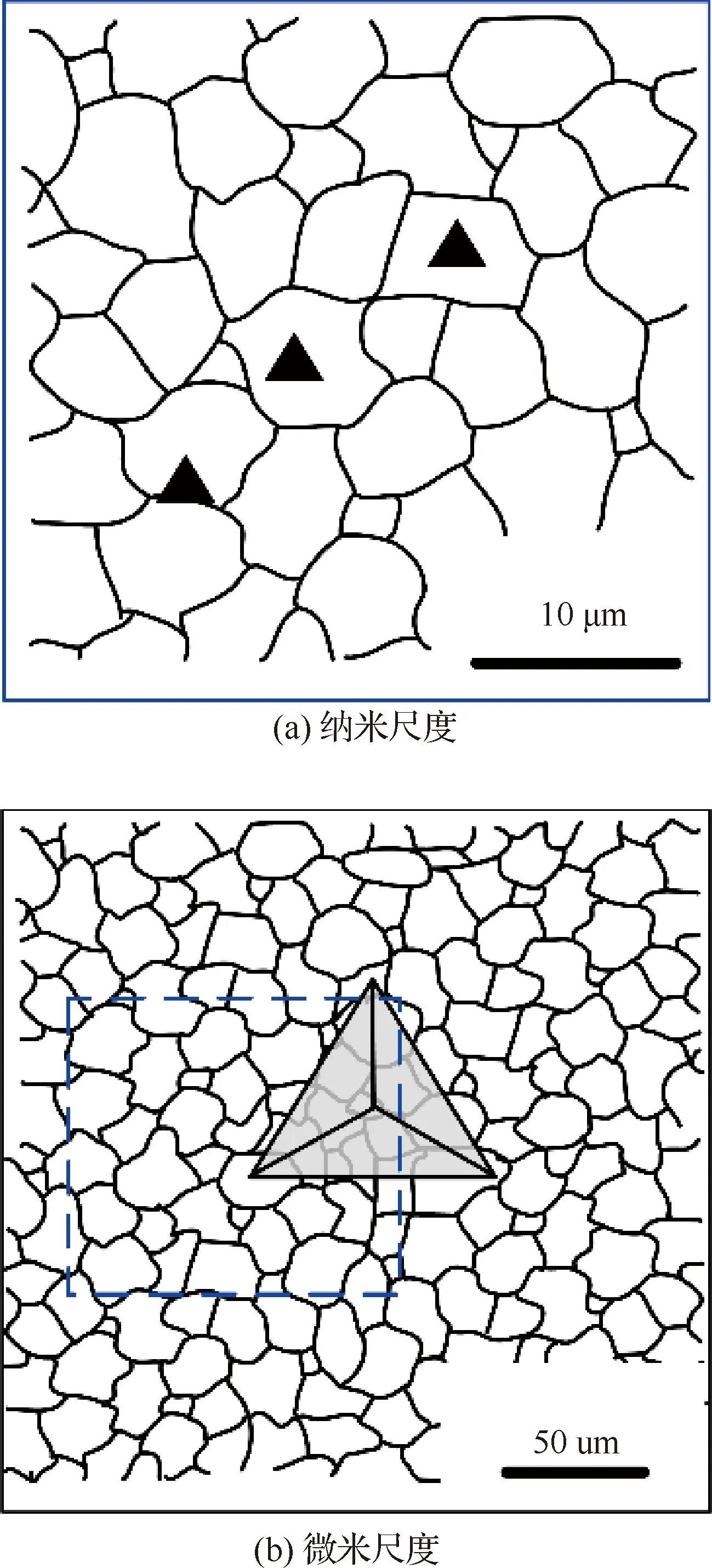
图5 玻氏压头压入多晶材料示意图Fig.5 Schematic of indentation on a polycrystalline material using a Berkovich indenter

观硬度的作用程度。然而，同时虑及宏观-微观-纳观3种不同尺度的研究尚不深入。

另一方面随着材料表征技术的不断发展，新的成像和表征技术作用尺度不断减小，为揭示材料新现象、新规律提供可能。自从1998年Nix和Gao等提出基于单晶金属材料几何必须位错(GND)的通用模型，ISE理论建模及多场耦合环境下ISE现象研究引起广泛关注[40-42]。式(20)和式(21)分别给出自相似的等效锥形压头Nix-Gao模型和适用于球头压头的Nix-Gao扩展模型[43]：

(20)

式中：h*为特征压入深度；Ho为宏观硬度；G为剪切模量；ρG和ρs分别为GND密度和统计存储位错(SSD)密度；c、b和r分别为泰勒因子、布拉格矢量和Nye因子，针对不同晶体结构时均为常数。如图6(a)所示，γ为锥形压头半锥角的余角(即γ+θ=90°)，同理，结合图6(b)所示，球头压头Nix-Gao扩展模型如下：

(21)

式中：R*为球形压头特征半径；R′为球形压头名义半径。

假设GND仅处于以a为半径的半球体内，根据式(20)和式(21)不难发现对于锥形压头GND密度与压入深度成反比，然而对于球形压头GND密度与压头半径成反比，与压入深度无关。下面仅以自相似压头为例，分析求解ISE模型的发展与局限性。

首先，经典的Nix-Gao模型已在微米尺度压痕测试中得到普遍认可，并被扩展到多物理场耦合环境下研究场强对ISE的影响，例如美国加州理工学院的Lee团队[44]对[0 0 1]取向的面心立方(fcc)和体心立方(bcc)单晶金属材料在160 K低温环境下发现温度对ISE存在显著影响，即测试材料的Ho和h*都与温度变量存在明显的函数关系。

图6 微纳米压痕压入示意图Fig.6 Schematics of micro- and nanoindentation

其次，经典模型仅考虑单晶纯材料，即忽略材料固有尺度作用，但是众所周知具有工程实际意义的往往是多晶、薄膜/涂层等材料，因此如前所述ISE将受到材料固有尺度的影响，典型的如图7[45]所示，湘潭大学周益春教授团队利用有限元方法分别对硬膜软基底(薄膜硬度Hf=5.07 GPa，基底硬度Hs=1.17 GPa)和软膜硬基底(Hf=0.72 GPa，Hs=12.75 GPa)单层膜材料考虑ISE影响下的薄膜固有硬度随相对压入深度的关系，并且类比Nix-Gao模型研究发现弹性模量与压入深度也存在如下关系[46]：

(22)

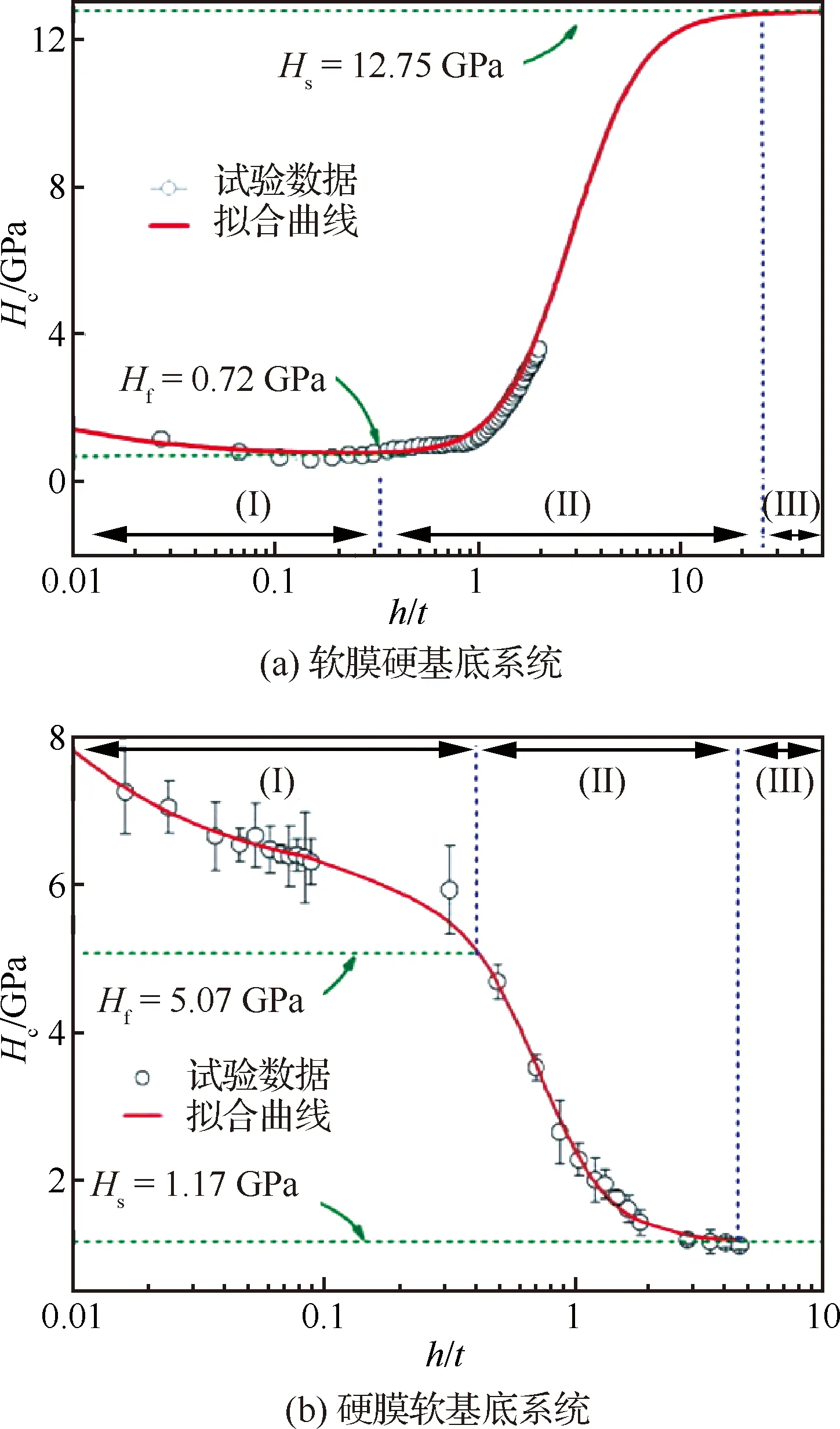
图7 复合硬度(Hc)与相对压入深度(h/t)函数图[45]Fig.7 Composite hardness (Hc) as functions of relative indentation depth (RID)[45]

如图8[40]所示，美国路易斯安那州立大学Voyiadjis等[40, 47]发现多晶材料由于晶界阻碍位错运动引起压入硬度不再随压入深度单调减小，而单晶材料则表现明显的单调性。

图8 单晶铝样品和多晶铝样品在0.1/s应变速率下的压痕响应对比[40]Fig.8 Comparison of nanoindentation response of a single crystalline Al sample with that of a polycrystalline sample at strain rates of 0.1/s[40]

最近研究材料在不同尺度、外部试验条件等耦合作用下求解ISE模型成为热点，比如英国莱斯特大学Gill和Campbell[38]利用球头压痕提取材料固有尺度，并将经典模型推广至多晶合金材料；美国路易斯安那州立大学Voyiadjis团队[41, 48]系统研究了典型双晶fcc金属材料在纳米压痕试验中存在的温度和速率压痕尺寸效应，以及基于应变梯度连续塑性理论有限元模拟揭示引起ISE的原因。此外，研究发现压痕尺寸效应也将直接影响其他力学参量的评估，比如屈服强度[49]等。

3 微纳米压痕测试应用

随着材料测试技术的不断发展，微纳米压痕测试技术逐渐发展成为一种高通量的力学性能测试方法[17]。然而，一方面由于材料真实服役环境往往与标准测试环境存在显著差异，此时测试出来的材料力学性能参数与真实服役环境下的存在很大的偏差；另一方面由于经典P-h曲线分析模型所需的假设前提可能在接近服役环境下的微纳米压痕测试技术中不在满足，从而引起较大的试验误差，甚至得到完全错误的结论(比如高温蠕变引起P-h曲线卸载段出现“鼻子”[50]，低温温漂效应引起P-h曲线严重右移[25, 51]等)。因此，致力于解决上述不足，纳米压痕测试技术迎来了新的发展机遇。

本节首先描述典型磁电弹性材料在力-电-热-磁多场耦合环境下接触力学模型，其次重点总结一些压痕测试技术在航空航天领域的应用研究及潜在机遇。

3.1 多场耦合接触力学模型

作为发展面向材料实际服役环境下的微纳压痕测试技术力学基础，典型磁电热弹性材料压痕问题日渐受到研究人员的关注[52-55]，并显著地促进微纳米尺度智能材料(如压电材料、形状记忆合金和磁致伸缩材料)的发展和应用。

针对压电材料的力电耦合压痕响应及压热弹问题早在20世纪90年代中期就已给出通解的计算方法，Ashida等[56]求解具有热效应的材料通解的一种常规方法是将热传导方程先行独立地求解，而后在通解中包含一个特解部分。区别于传统的压痕接触力学，需要额外引入电场矢量，包括压热弹性势函数、压弹函数、压电函数和电势用以描述耦合环境下的弹性场本构方程，进而推导出位移分量、场强分量、应力和电位移分量。

然而，上述方法得到的通解是由几个势函数构成的，由于势函数并不都是调和函数，因此导致一些研究结果无法直接应用[57]。浙江大学Chen等[58]首次将热传导方程与其他方程组耦合处理，进而重构出通解。研究发现此时计算获得的通解仍由多个势函数构成，但它们都是调和函数。通常求解热弹性或者压痕问题的数学方法除了势函数法[52]以外还有Hankel变换[59]和格林函数法，其中势函数法已经被被广泛应用到求解考虑热效应的三维裂纹问题以及压痕问题。

此外，考虑表面应力、表面磁电弹性效应及接触摩擦效应等影响因素对经典磁电弹性效应(MEE)通解模型进行补充推广[53, 60]，有助于研究纳米科学和纳米技术领域的成像机理[59](如压电响应力显微镜，PFM；磁电响应力显微镜，MFM)，并对多铁薄膜、锂离子电池单元、功能梯度磁电弹性等多相复合材料的压痕响应数值模拟提供理论支撑[53, 61-62]。

3.2 高/低温纳米压痕测试

众所周知，航空发动机作为飞机的“心脏”，其核心零部件涡轮叶片服役于恶劣的工作环境(高温、复杂应力)，对所用高比强度、高比刚度、轻质材料高温力学性能提出更为严苛的要求[63-65]。此外，热防护材料是运载火箭及高超声速飞行器在极端环境下安全服役的基石，研究其高温耐久性、氧化失效机理及可靠性对提高飞行器的生存能力有极大地推动作用[66-67]，例如美国哥伦比亚航天飞机的失事就是由于热防护系统的破损直接导致的。同时，飞行器在太空、月球或者其他星体表面考察作业时，表层防护材料往往需要承受交变温度载荷作用(比如月球表面温度-153 ℃～107 ℃)，而服役于航天器低温推进系统的液氢/液氧、液氧/烃类燃料贮箱绝热材料、密封材料往往承受低于-150 ℃[68-69]，例如挑战者号航天飞机O型密封圈低温硬化导致爆炸，造成直接损失12亿美元。因此，发展在高/低温加载环境下的纳米压痕测试能为研究材料在服役温度下的变形行为以及服役寿命预测提供重要理论支撑。

在过去的十几年来，如图9[18,70]所示，一些商业化及自制高/低温纳米压痕测试仪器被研制出来，温度范围从大约-150 ℃～1 100 ℃[18, 25, 44, 70-72](高/低温宏观压入测试仪器不在讨论范畴之内，比如北京大学与吉林大学合作开发的温度最高可达1 600 ℃的仪器化压入测试装置[73])，这其中包括集成在SEM腔室内的小型高/低温原位纳米压痕测试仪器，该仪器可实时原位监测压入过程中的压头与测试样品表面间的接触微区的滑移带扩展、表面材料剥离以及裂纹萌生等变形机制[74-75]。

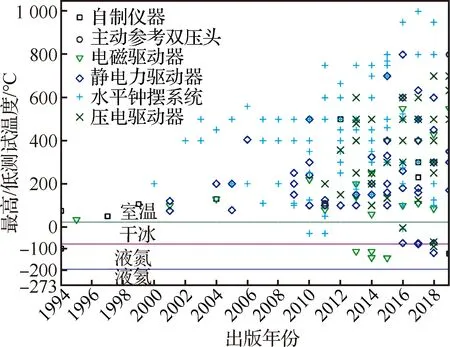
图9 近年来基于不同驱动原理的小尺度测试仪器的最高/低温度[18, 70]Fig.9 Maximum or minimum temperature of small-scale testing instruments based on different driving principles in recent years[18, 70]

高/低温纳米压痕测试技术为研究基于温度影响下材料相变、位错成核、剪切带激活以及材料脆-韧性转变机制提供有力工具[76]。其中，高温纳米压痕测试技术已经发展了近20年，被广泛应用于研究不同温度加载条件下热障陶瓷涂层、高温合金以及半导体材料的力学性能演化机制[73,77-80]，比如清华大学冯雪教授课题组利用基于氛围环境加载方式的高温纳米压入测试装置(Bruker TI 950)提出基于化学-机械耦合氧化机制，重点研究了扩散控制氧化过程中的应力-扩散耦合效应、纳米压入试验中氧化物形貌的应力诱导演化以及沿晶断裂裂纹前沿的应力氧化作用机制[81]，3种不同氧化处理过程的残余压痕尖端裂纹产生情况如图10[82]所示，其中仅在保载过程中进行氧化时观察到残余压痕裂纹的萌生，揭示了应力-扩散耦合氧化效应；瑞士联邦材料科学技术实验室的Wheeler团队，利用自制可集成在SEM腔室内的高温纳米压痕仪器，通过平压头作用在FIB切割出的微柱上(即微柱压缩试验)可直接观测到单晶硅受温度影响下的脆-韧转变行为[75]，现在他们所研制的高温纳米压痕仪器已实现产业化(Alennis®原位纳米压痕仪器)。

图10 残余压痕尖端区域形貌的透射电镜(TEM)图[82]Fig.10 TEM images showing morphologies in the tip area of residual imprints[82]

然而，正如香港大学的Feng和Ngan[83]研究发现接触温漂和蠕变效应直接影响到弹性模量的测试，尤其在800 ℃以上，P-h曲线卸载区域表现显著的负刚度现象(如图11[50]箭头所示)，关键原因在于蠕变效应，这一问题即使对于商业化仪器也同样存在。基于Ngan修正模型可知真实接触刚度(S)和计算值(Su)为

(23)

式中：P′为卸载速率；h′u为卸载段初始位置的位移率。

图11 800 ℃下镍基单晶合金典型P-h曲线[50]Fig.11 Typical P-h curve on single Ni-base alloy at 800 ℃[50]

但是800 ℃以上式(23)计算值偏大甚至仍为负值，因此清华大学冯雪团队[50]结合宏观幂律蠕变模型给出适用于800 ℃以上的蠕变修正模型：

(24)

式中：κ为一个无量纲正指数。

另一方面，消除压头与样品作用区域的接触温漂是耦合温度场的微纳米压痕测试技术基础。根据麻省理工学院Lee等[84]的研究，可通过式(25)计算从初始时间至t0时刻的一维温度漂移平均速率(U′)。

(25)

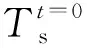
此外，从图9中不难看出，低温纳米压痕测试仪器发展兴起还不足10年，但是其已经在半导体材料相变研究、低韧-脆转变温度材料(比如纯锡)脆性断裂行为等研究中发挥着不可替代的作用，也为拓展纳米压痕测试理论提供新的机遇[86-87]。比如加州理工大学Lee团队利用自行组装的用于SEM下具有原位低温纳米压痕测试装置，对多种单晶金属材料(包括bcc结构的铌和钨；fcc结构的铝和金)低温下的ISE进行研究，发现温度作用下的尺寸效应不再满足于经典的Nix-Gao模型[44]；吉林大学赵宏伟教授团队自主研制的低温纳米压痕仪器如图12(a)[51]所示，首次根据统计规律(图12(b)[88]和图12(c)[88])发现温度加载范围从292 K降至210 K，(1 0 0)单晶硅纳米压入P-h曲线卸载段出现“突退(pop-out)”现象逐渐降低直至完全转变为“肘弯(elbow)”现象，结合拉曼光谱对残余压痕的测试，发现此时仅存在α-Si相而不再产生Si-Ⅲ/Ⅻ混合相，证明低温直接影响单晶硅在压痕卸载段的相变产物[88]。

值得一提地，赵宏伟教授团队[51]系统地提取低温纳米压痕仪的温度漂移速率，并提出削弱温漂的长时间预接触、接触铜线及低热扩散系数压头等方法。同时，针对hcp单晶蓝宝石压头，该团队详细讨论温度对压头力学参数及压头形状参数的影响，进而评估由此引起的弹性模量和硬度计算误差，如图13[51]所示。

图13 温度对压头及弹性模量的影响[51]Fig.13 Influence of temperature on tip and elastic modulus[51]

然而，由于低温微纳米压痕测试仪器开发周期长、测试成本高等原因导致其在航空航天材料测试领域的应用研究尚未见报道，并且通常被低温宏观力学测试替代，但是低温服役材料微区变形损伤及失效机理的研究对研发新材料有着关键作用。

3.3 电/磁场耦合条件下的纳米压痕测试

随着微机电系统(MEMS)及半导体行业的兴起与发展，功能材料(比如铁电材料、铁磁材料等)在应力/应变作用下的电/磁响应越来越受研究人员的关注。其中，有研究表明铁磁性/碳材料复合物不仅兼顾比重小、力学特性及耐候性好，并且利用铁磁性材料良好的磁导特性，能够干扰雷达吸波剂的选择，从而实现飞行器的隐身效果[89]，因此开展功能材料在电磁场耦合作用下的纳米压痕试验，研究力学加载对电磁特性影响等具有国防战略意义。

不同于传统宏观力学测试装置需要大型电磁场发生设备及特殊设计的电磁屏蔽夹具[90]，电/磁场耦合条件下的纳米压痕测试装置通常仅需更换特定压头并构成封闭的电/磁回路即可，特别是可以认为电学信号能够实时反映压入过程中的细节信息，换句话说电学信号的变化规律也可以作为一种原位监测手段[91]，比如2.2节所述的最大压入深度下接触面积可以根据实时电阻测量变化量(或电压-电流变化曲线)进行计算[92-93]，典型的通电纳米压痕测试仪器示意图如图14(a)[92]所示。

图14 典型电磁场耦合作用下的纳米压痕测试装置Fig.14 Representative nanoindentation testing devices coupling with electromagnetic filed

另外，通电纳米压痕测试也为在纳米尺度上研究半导体材料(比如硅、锗及砷化镓)在机械载荷作用下的变形机制、相变和电学响应提供技术手段，比如Pharr等[94]通过原位电学表征技术研究单晶硅纳米压痕过程中变形行为，由于电学信号对压入过程中局部Si-Ⅰ相变为Si-Ⅱ特别敏感，通过原位电学表征测试研究人员对单晶硅压痕加载和卸载过程中变形过程的演化有了更深的理解；Nowak等[95]对砷化镓纳米压入过程进行原位电学监测，有机地建立P-h曲线中的Pop-In现象与检测电流尖峰的联系，并且电流的陡增揭示了砷化镓发生由于压力引起的相变现象，推动研究人员对砷化镓塑性变形机制的深入理解；Nguyen等[96]在纳米压痕测试过程中实时测量接触电阻以监测压入过程中导体-半导体试样的分层失效现象，接触电流的突降与薄膜材料分层以及P-h曲线中的Pop-In现象相关。同时，原位通电纳米压痕测试技术也已用于表征功能材料机电响应特性[97]。

涉及电场和磁场共同耦合作用下的纳米压痕测试技术仅兴起于最近10年间，但是已经在铁电铁磁等对电磁场敏感的功能材料研究方面起到重要作用[98-100]。图14(b)[101]为北京大学方岱宁团队和吉林大学赵宏伟团队合作研发的电磁场耦合作用下的纳米压痕测试装置示意图。针对层状电磁复合材料LSMO/PMN-PT和PMN-PT/TbDyFe分别进行电场和磁场调控作用下的纳米压痕测试，其中不同场强作用下的P-h曲线如图15[102]所示，同时基于量纲分析方法发现了耦合电/磁场下的块体、薄膜等材料压痕耗散功与压入总功比值和硬度与弹性模量之间存在明显的线性尺度关系[99]：

-dkM+(k+l-kη0)

(26)

式中：M为场强强度；η为压痕耗散功；d和η0可由η-M拟合曲线计算获得；k和l为线性尺度关系拟合常数。

图15 电/磁场对纳米压痕行为的影响[102]Fig.15 Effect of electric/magnetic field on nanoindentation behavior[102]

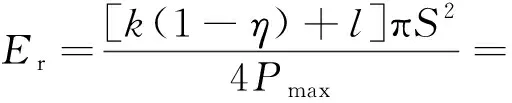
(27)

(28)

结合式(27)和式(28)可以直接确定电/磁场耦合作用下的材料力学性能，利用能量法能够有效地避免pile-up现象引起的接触深度计算误差[97]。此外，研究发现电/磁场对铁电/磁材料硬度、折合模量以及压痕能量耗散等力学参数有明显的调控作用[102]，这将间接推动铁磁性材料在隐身涂层开发领域的应用。

4 问题与挑战

尽管接近服役环境下的微纳米压痕测试技术已经取得了如前所述的重大突破，但是面临的问题与挑战仍然不容忽视，尤其针对测试仪器开发、测试数据可靠性保证以及分析方法的修正和发展。

对于再现服役环境加载功能的硬件集成、收发信号以及控制软件兼容处理就是面临的首要问题。一方面，无论是温度场加载还是电/磁场加载，通常都需要在微纳米压痕测试系统机械本体上装配调试。通常高温加载可以选用非接触的辐照加热方式[72]，磁场加载也无需压头与样品直接接触磁极，然而电场和低温的加载则恰恰相反，尤其对于-150 ℃以下的低温加载直接或间接接触制冷可能是唯一稳定可靠的方式[103]，因此需要合理布局、优化装配空间。另一方面，服役环境也将直接影响仪器化纳米压入测试系统精密传感器及驱动器信号的采集、记录和控制，比如超出传感器正常工作温度范围所产生非线性的漂移、复杂电磁环境导致载荷/位移噪声水平的显著增加等。另外不可否认的是对于接近服役环境下的纳米压痕仪器的控制系统还不完善，尤其对于研究机构自制测试仪器的功能及控制模式并不可靠，因此开发更有效的控制系统对复杂仪器设备显得尤为重要[104]。特别是针对诸如Bi-2233等超导材料服役环境的重构，由于涉及温度场与电/磁场同时耦合加载，这对纳米压痕测试仪器稳定性提出了更高的挑战。

其次，服役环境的重构将给整个纳米压入测试过程带来很多潜在的风险及不确定性(甚至影响结果的判断)。以高/低温纳米压入过程为例，温漂控制、温度均匀性、化学稳定性以及材料物性稳定性已被研究人员广泛关注[25, 72, 84, 105-107]，比如图16(a)[51]揭示了低温加载环境引起单晶锗压入过程中的温漂现象；图16(b)[105]发现熔融石英在不同温度下纳米压入过程中的温漂现象；图16(c)[84]和图16(d)[84]利用有限元仿真方法发现纳米压入塑性区域内温度不均匀性。另外，温度场加载不仅会影响到测试材料表面物性改变(产生氧化层或者结冰)，也同样对压头物性产生影响(比如加速磨损，热胀冷缩引起接触面积变化等)[105, 108]。

图16 在高/低温环境下典型材料温漂测量及接触微区温度分布Fig.16 Measurements of thermal drift for representative materials at high/low temperatures and contour plots of temperature at contact region

最后，经典分析方法可能对测试获得的P-h曲线数据处理不再直接适用，选择合适的分析模型或者采用修正处理是极为必要的，比如基于量纲分析方法计算电/磁耦合作用下铁电/铁磁材料的力学性能[102]、基于Tang-Ngan模型修正高温蠕变引起的负刚度现象[50]以及基于量纲分析方法修正高温Pile-Up现象引起的接触面积误差[109]等。此外，如前所述针对典型磁电弹性材料(即压电/铁电材料)力-电-热-磁多场耦合环境下接触力学模型已被不断完善与推广，但是相关报道往往集中在理论推导及数值模拟验证方面，很少有用于解释多场耦合环境下微纳米压痕试验现象和结果的研究。如何将力学理论用于指导测试技术和方法的发展值得思考。

5 结论与展望

本文重点讨论了接近服役环境下的微纳米压痕测试技术所取得的发展和应用。尽管微纳米压痕测试技术方法已经标准化(ISO 14577、ASTM E2546、GB/T 21838等)，但是面向航空航天领域的高/低温、电/磁场等多物理场耦合条件下的微纳米压痕测试技术仍处于起步阶段。在许多方面仍需要进一步研究探索，主要包括：

1) “工欲善其事，必先利其器”，目前国内高精度纳米压痕测试仪器主要依赖于国外进口，这将严重制约面向国家重大战略需求的基础性研究工作进程，因此研发具有自主知识产权、工程化应用背景的微纳米压痕测试仪器装备是国内科学界与工程界共同面临的重大而迫切的任务。

2) 基于目前微纳米压痕测试技术所取得的研究成果，常规压痕测试技术已趋于成熟。接下来如何构建更为接近材料真实服役环境(比如模拟太空中极低温、强辐照环境等)的微纳米压痕测试系统将成为新的发展方向，亟待解决的关键问题包含：① 再现服役环境加载功能的硬件集成、并行检测与协同控制以及复杂电/磁环境兼容技术；② 多物理场耦合作用下材料微纳米压痕测试数据分析模型及其与微观组织结构演变规律的映射关系。

3) 近年来常规微纳米压痕测试技术已在高速纳米压痕提取材料力学参数(如硬度和弹性模量)分布图上取得新的突破。这种高度局部化力学性能的海量数据集有助于研究多相材料显微组织特征与力学性能之间的联系，然而目前尚缺乏高速纳米压痕在多物理场耦合环境下的试验应用。

4) 经典数据分析方法的局限性已经被研究人员广泛关注。此外，涉及高/低温、电/磁场、高应变速率、强辐照环境等多物理场耦合作用下压痕测试表征方法尚未系统的建立，缺乏行业内的测试标准与技术规范。因此，在未来研发集成化程度更高、测试更为可靠并且面向材料更为真实服役环境的微纳米压痕测试方法有望为材料测试领域提供更多新颖的应用机会。