AutoScan系列复杂零件自动化三维测量装备开发与应用
李中伟,张攀,钟凯,李文龙
1. 华中科技大学 材料科学与工程学院 材料成形与模具技术国家重点实验室,武汉 430074 2. 华中科技大学 机械科学与工程学院 数字制造装备与技术国家重点实验室,武汉 430074
航空发动机机匣、叶片等关键零件形状复杂,成形精度难以控制,其制造水平代表国家的核心竞争力。三维测量不仅能够实现复杂零件的精度检测,还可为后续工艺优化提供基础数据,是保证复杂零件成形制造精度的关键技术。“中国制造2025”“德国工业4.0”等战略规划均阐明了工业零件三维测量和精度检测对于发展高端制造和智能制造的重要性,并将其列为重点研究内容。
现有自动化三维测量方法主要有线结构光法[1-2]和面结构光法[3-6]两类。线结构光法通过向被测物体表面投影线条获取一条线的三维数据,结构简单,测量精度高,但在效率方面存在较大局限。面结构光法向被测物体表面投影光栅条纹图案获取一个形面的三维数据,结构相对复杂,但测量速度快,数据密度大,是进行自动化三维测量的首选方法。基于面结构光和机器人的自动化三维测量技术,由机器人按照预先规划的测量视点和测量路径带动面结构光三维测头,从多个视角对复杂零件进行自动化三维测量[7-8],具有速度快、精度高等优势,是实现自动化三维测量的主流技术之一。
国内外许多机构对此技术进行了深入研究,并开发了相应的自动化三维测量装备,在航空、汽车等领域的复杂零件精度检测方面进行了推广和应用[9]。如:GOM公司研发的ScanBox系列自动化三维测量装备,可对航空发动机风扇叶片上的关键表面区域进行检测,达到微米级精度[10];Hexagon公司所研发的PartInspect L系列自动化三维测量设备,已应用于航空、航天等多个领域,精确重建出航空发动机叶片、叶盘零部件的轮廓形状和细节特征,进行误差分析[11]。除上述产业化公司外,天津大学、北京航空航天大学、华中科技大学与加拿大多伦多大学等学术机构在自动化三维测量技术方向也取得了良好进展。如:天津大学的杨守瑞[12]提出了一种基于面结构光和近景摄影测量技术的大型构件复杂曲面三维测量方法,结合工业机器人运动规划,实现了飞机蒙皮、汽车车身等大型复杂曲面的高精度自动化测量;多伦多大学的Liu等[13]提出一种3D扫描仪-机器人校准方法,降低了连续测量期间的数据拼接误差,有效提高了自动化测量的稳定性。
已有的自动化三维测量技术和设备在实际应用时仍存在以下问题:① 复杂零件的自动化测量视点规划仍以人工示教为主,规划效率低且难以获得最优视点;② 结构光三维测量设备的标定仍以离线标定为主,当应用于具有复杂工况的生产现场时,预先标定的系统参数易发生漂移,导致测量精度低;③ 多视测量数据拼接仍主要采用标志点拼接的方式,过程繁琐,且难以应用于高温零件自动化三维测量场景;④ 数据自动处理过程中,受工装夹具等支撑影响,测量数据中存在大量点云背景噪声,影响数据自动处理时的精度与稳定性。针对上述问题,国内外学者围绕测量视点自动规划、系统参数标定、多视点云配准、点云数据自动处理等关键技术开展了深入系统的研究,以进一步提高测量精度和自动化程度。
在测量视点自动规划方面,现有方法主要有产生-筛选、专家模式、综合模式等,其中产生-筛选模式算法简单,对参照模型依赖较小,应用前景良好。Sheng等[14]提出一种“平坦补丁”法(Flat Patches)针对平坦工件进行视点划分,在测量表面曲率较小的工件时具有良好的效果,但难以适用于表面曲率较大的工件。Chen和Li[15]提出一种将对象特征作为与表面法线相连的单个点进行重采样,然后以基于最小-最大标准的遗传算法计算最佳视点的方法,可适用于各向特征一致性较好的工件。Germani等[16]依据知识数据库,根据要验证的公差表面计算最佳视点位置,针对特定物体时效果较好,但通用性较差。Lartigue等[17]提出基于体素的测量路径规划方法,将零件表面划分为体素贴图,然后以可视性与测量质量为标准生成视点,与前几种方法相比,在零件复杂度适应性方面具有更好的性能,但其可视性计算方法仅针对单目面结构光三维测量设备,难以应用于更加广泛的双目面结构光三维测量设备。总体而言,前述几种方法大多在针对具有某些特定特征的被测零件进行测量视点规划时具有良好的效果,但在零件的普适性方面尚有诸多限制。
在测量系统参数标定方面,现有的方法仍以离线标定[18-21]为主,效率低且过程繁琐,难以应用于具有复杂工况的生产现场。Garbacz[22]、Dang[23]等将测量与标定同时进行,提高了标定的效率,但需使用特殊设计的精确标志点以保证匹配点对质量[24]。针对基于相位测量原理的面结构光技术可通过相位相关提供大量精确匹配点的特性,一些学者在测量中根据相位相关方法直接获取匹配点进行标定[25-29]。Bräuer-burchardt等[27-28]提出一种系统重标定方法,补偿了传感器和机械设备影响导致的标定误差。Zhao等[25]提出一种基于光束平差和相位匹配的双目相机实时标定算法,实现了大规模的精确测量。前述几种方法一定程度上可以提高参数标定的效率与精度,但通常要求光学几何参数有初步标定,且需使用大量匹配点对矫正光学几何,应用有所局限。
在多视测量数据拼接方面,现有方法主要为标志点拼接法[30],拼接精度高但过程繁琐,测量效率低。为此,有学者提出直接配准方法,采用顺序帧点云之间的特征、距离等约束进行配准,适用于具有复杂特征的零件,灵活程度高,但全局配准精度仍然较低。Newcombe等[31]提出一种基于Kinet传感器的配准方法,采用隐式阶段距离函数(TSDF)对测量点云进行融合,并利用光线投射算法实时获取重建模型表面数据,与当前帧进行配准实现实时定位跟踪,显著提高了单次配准的精度。Lefloch等[32]在其基础上以表面最大绝对曲率为参数计算误差权重,有效提高了单次配准精度,但其计算依赖于经验参数,难以适用其他复杂场景。前述两种方法可以提高单次配准精度,但难以消除全局配准累计误差,因此有学者采用全局优化算法对全局视点位姿进行优化。Henry[33]和Dai[34]等采用光束平差法(Bundle Adjustment,BA)算法优化全局视点位姿,但只针对稀疏三维点与视点,且依赖于纹理特征检测。Zhou[35]和Whelan[36]等采用非刚性配准方法将分层、错位点云进行扭曲变形,使得整体重建结果与局部形状一致,但对精度会造成严重影响。Lu和Milios[37]采用位姿图方式将全局位姿优化问题建模,以视点位姿为节点,两个节点之间点云配准结果为边,大幅提高了配准效率。Cao[38]和Yue[39]等在此基础上针对不同应用场景的重建点云进行配准优化,但未考虑配准点云的距离误差,仅对视点位姿与视点间相对位姿不一致进行优化。上述几种方法在顺序帧间配准精度和全局优化方面取得了较为良好的效果,但其关注的重点在于拼接数据的视觉效果,易造成重建点云表面形状失真,难以适用于工业零件的高精度三维测量。
在点云背景噪声自动去除方面,现有方法主要为将测量点云与CAD模型配准后按照距离准则去除点云背景噪声,但实际应用时由于点云背景噪声与被测物体点云紧密相连,导致配准过程难以收敛,影响数据自动处理的精度与稳定性。程云勇等[40]结合模型配准可靠性原则,在基准CAD模型上对配准基准点进行预规划,降低了噪声、体外孤点等无关数据造成的误匹配影响,其配准精度依赖于配准基准点的规划。Chetverikov等[41]将截断最小二乘法应用到对应点匹配中,选取欧氏距离排序靠前的部分匹配点对进行计算,可有效降低无关数据的影响。Jian和Vemuri等[42]采用高斯混合模型对点云配准算法进行建模,大幅降低了无关数据对配准点影响,但计算量大、花费时间长,难以满足实际工业生产需求。本课题组的程旭等[43]结合三维形状指数度量标准与非极大值抑制方法,优化选择具有高曲率特征的匹配点对进行配准,降低了噪声等无关数据对点云匹配的影响。上述几种方法在背景数据较少时具有良好的效果,但当背景数据过多且与物体紧密相连时仍会产生误匹配,致使配准过程无法收敛。
针对以上4个方面的问题,本文将系统介绍基于双目测头的自动化测量视点规划、基于耦合焦距比例约束的系统参数自标定、基于全局优化的多视测量数据拼接、基于自适应阈值ICP的点云背景噪声自动去除等关键技术;在此基础上,进一步介绍AutoScan系列自动化三维测量装备的研制,包括PowerVirtualPlan视点规划软件、PowerScan三维测量软件、iPoin3D数据处理软件的开发;最后介绍自动化三维测量装备在航空航天等领域的工程应用情况。
1 自动化三维测量关键技术
1.1 基于双目测头的测量视点规划技术
当前工业测量中多将面结构光技术与机器人技术结合以实现多个视点的自动化测量,获取大型工件的三维数据。现有设备一般采用人工示教对机器人进行视点规划,但效率低且安全性、稳定性无法保证。
为此,本文提出一种基于双目测头的测量视点规划技术,以实现复杂零件的自动测量。首先以双目测头单次最佳测量范围作为体元对模型进行区域划分;其次,根据体元六面等价原理将体元划分为6个视图,针对每个视图均匀生成候选试点;然后根据特征可视性及视角方向计算视点三维成像质量,筛选最佳成像视点;再建立机器人与测头的统一模型进行模拟仿真以判断视点可达性,得出最优视点,保证测量时机器人不发生机械干涉;最后对不同体元区域的视点进行全局统一,以机器人运动代价最小化为依据生成最佳路径。
为方便说明,以“测头”作为双目相机加投影仪的代称,测头中心为双目相机基线中心,测头视点位置即测头基线中心位置。生成视点时,需获取视点的三维坐标及测头姿态。为简化描述,默认测头基线与体元x-y平面平行,测头姿态为其基线与体元中心所决定的平面,默认测头左相机处于相对视点方位角增大的位置,光轴方向指向体元中心。为更好获取模型表面特征,采用非均匀有理B样条(NURBS)模型进行视点划分。对提取出来的每一特征曲面进行如下定义:S为曲面面积;Pc为曲面中心点,即曲面轮廓线上所有的顶点坐标值的平均值;niavg为第i个分区曲面法矢量,即轮廓线上所有顶点法向量矢量和的单位化矢量。
首先将双目测头的单次最佳测量范围作为体元,对模型进行划分。采用双目相机测量时,无需对投影仪进行标定,仅需考虑双目相机测量范围。双目相机的三维重建主要通过极线约束,寻找到两张图像上的对应像素点,再依据相机的内外参数重建出三维点云。为保证重建精度,其最佳测量范围需满足两个约束条件:① 处于双目相机的共同测量区域;② 处于双目相机的共同测量景深。因此,双目测头的单次最佳测量范围可定义为以景深为直径的球的外接立方体,据此对模型表面进行体元划分。
区域划分完成之后,对单个体元生成视点。如图1所示,测头的最佳测量位置多定义为两个相交光轴的交点或公垂线的中心处,但考虑测量时仅需测量表面,所以将最佳测量位置调整为光轴交点垂直于测头中心反向的1/4景深处。因此,测头的视点位置可以定义为一个以体元中心为中心,最佳测量距离为半径的球面。体元的6个 面相互等价,因此将其分为前、后、左、右、仰、俯6个视图以方便规划。每个视图中选取一部分测量区域作为候选视点的生成区域,如图2中俯视图所示红色区域,天顶角α∈[0°,60°],方位角β∈[0°,360°]。另一部分区域在多个视图中是重合的,重合天顶角度为15°,足以保证零件特征的完整性。如图3所示,在视点生成区域,先均匀产生初始候选视点,生成准则为天顶角和方位角间隔角度为15°。
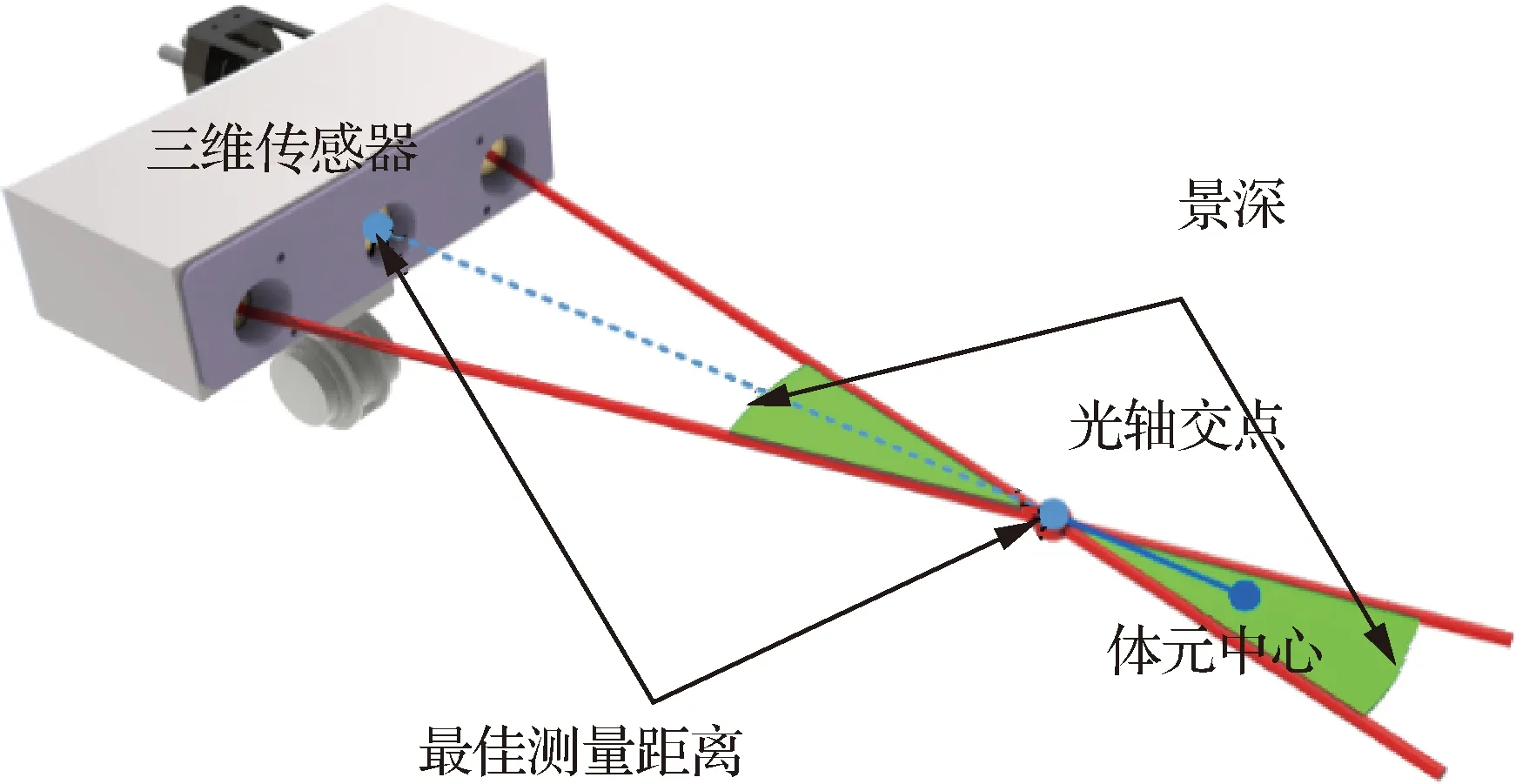
图1 双目测头最佳测量区域Fig.1 Optimal measurement area of binocular probe
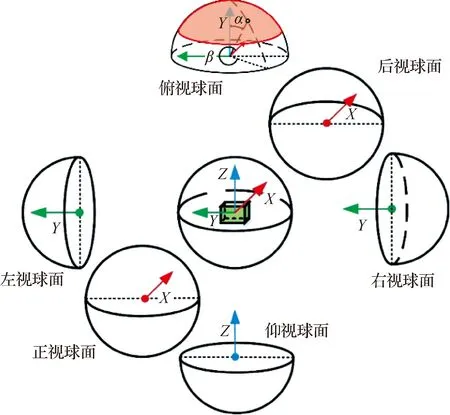
图2 体元测量区域划分Fig.2 Division of voxel measurement area
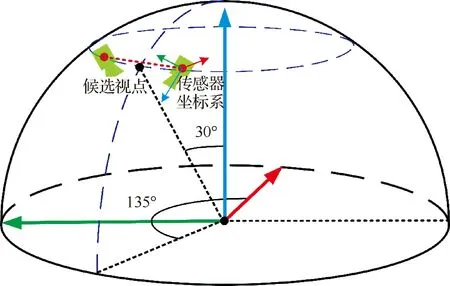
图3 单个体元俯视图的候选视点生成Fig.3 Generation of candidate viewpoints from a single voxel’s top view
初始候选视点生成之后,需根据其三维成像质量进行排序,筛选评估出最优成像视点。视点三维成像质量由对应特征的可视性及视角方向二者共同决定,因此需先判断对应视图测量区域所拥有的特征。划分流程如下:① 计算出特征曲面的平均法矢niavg;② 依据法矢方向所对应的天顶角与方位角进行视图划分,以正视图为例,法矢方向应为α∈[45°,135°],β∈[135°,225°];③ 若该视图分区内特征的曲面面积之和小于总面积的5%,则该分区对应的候选视点组不参与最优视点的筛选。特征划分完成之后,三维成像质量计算为
Fiq=mfvis+nfang
(1)
式中:Fiq为三维成像质量;fvis为特征可视性,代表该视点下光学可视特征的总面积;fang为视角方向参数,代表对应特征的测量效果;m、n为两个参数权重,分别设置为0.6、0.4。fvis的表达式为
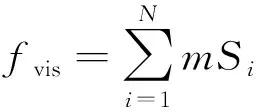
(2)
式中:Si为分区中特征的曲面面积,其取值表示为
(3)
发生干涉的判断准则为:依次连接曲面中心点Pc与视点、左相机中心、右相机中心,判断连线是否被曲面模型遮挡。fang的计算为
fang=tγ
(4)

(5)
θ=arctan(navg·npr)
(6)
式中:npr为测头法向量,由测头中心与体元中心连线决定;t为权重系数,不同的角度特征成像质量不尽相同;γ为比例系数,与特征可视性大小进行匹配;navg为面积加权法向量,代表着此视点下所有曲面法向量的加权方向,计算公式为
(7)
式中:niavg为第i个分区曲面法矢。
因此,可按照Fiq的大小对视点进行排序,从高到低依次验证视点可达性,选择最优视点。
最优成像视点筛选完成后,还需进行可达性判断,若无问题则生成最优视点,若存在问题则按照排序替换该视点。视点可达性的检测主要依靠机器人模拟仿真进行判断,其准确性依赖于机器人手眼标定的精度。为此,建立机器人与测头的统一模型,将测头位姿作为机器人的末端姿态,拍摄标定板进行定位构建转换关系以实现参数标定,从而更加方便地进行模拟。模型构建完成之后,通过机器人仿真进行碰撞检测以判断运动过程中是否存在机械干涉,确认视点可达性。
最佳视点构建完成后,还需进行视点的最优运动路径规划,以保证自动化测量的效率。本文先针对每个体元区域进行路径规划,以机器人的各轴转动角度之和最小为准则获得局部最优路径,然后将这些局部路径进行全局优化,得到全局路径。
如图4所示,通过对视点成像质量的计算和排序,以及可达性验证,能够获得一组可行的测量视点,并依据该组视点进行实际测量。测量结果中,转向节本体以外的数据为工装夹具,手动去除后进行配准,计算得到的数据覆盖率为91.3%(未获取数据多为夹具遮挡部分)。
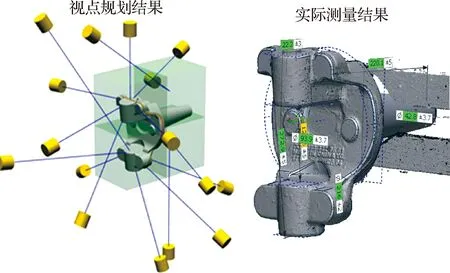
图4 测量视点虚拟规划与实际获取结果Fig.4 Results of viewpoint virtual planning and actual acquisition
1.2 基于耦合焦距比例约束的系统参数自标定算法
面结构光三维重建技术基本流程如图5所示,测量时,投影仪向被测物体表面投影多个频率的光栅条纹图案,相机同步进行拍摄。由于被测物体表面的几何形状变化,相机所拍摄的光栅条纹图案会发生变形,进而再根据算法依次进行相位计算、相位展开、立体匹配,最终按照三角测量原理重建出三维点云。三维重建算法依赖于预先标定的相机参数,实际使用时受工业现场高温、环境振动等因素影响会发生漂移,导致重建精度不稳定。

图5 面结构光三维重建原理图Fig.5 Schematic diagram of 3D reconstruction of surface structured light
为此,本文提出一种基于耦合焦距比例约束的系统参数自标定算法,实现变温、振动等复杂工况的高精度稳定测量。首先向被测物体表面投影多幅水平和垂直光栅条纹图像,通过四步相移算法进行解相求得相位图,再通过相位相关性原理进行对应点匹配,实现系统参数自标定,基本原理如图6所示,匹配函数为
(8)
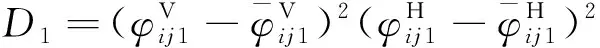
(9)
(10)
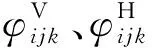
(11)
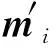
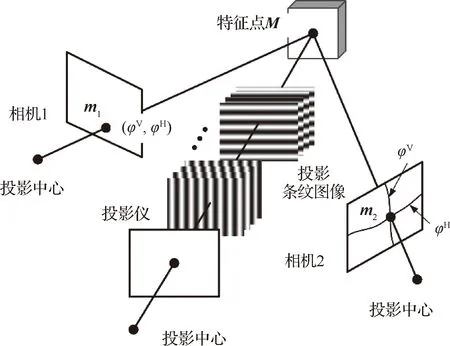
图6 相位匹配示意图Fig.6 Schematic diagram of phase matching
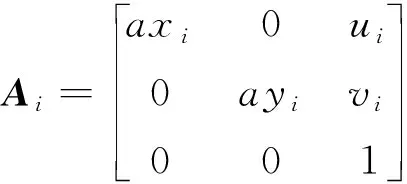
(12)
左右相机之间的位姿关系可定义为刚性变换,通过旋转平移矩阵进行表示。左右相机的图像则可根据极线几何关系,通过基础矩阵F进行关联:
(13)
式中:F为基础矩阵;[t]x为t向量定义的反对称矩阵;[t]xR为本质矩阵E,下标1和2分别代表左右相机。
将相机成像视作理想模型,则可通过经典的八点法求解出本质矩阵。为提高精度,可通过SNR对匹配点对进行筛选,去除低质量的匹配点对,从而计算出相对精确的相机相对位置。根据相机相对位置与相机初始内部参数对匹配点对进行三维重建,获取初始三维结构。但由于相机的内参只是进行粗略估计,因此三维结构并不准确,需进行优化,经典的最小重投影误差优化函数为
(14)
为验证参数自标定算法的精度与稳定性,本课题组搭建了一套基于面结构光技术的三维测量系统,在其加热过程中采用本文所提的自标定算法优化参数,针对标准陶瓷球棒进行连续多次测量,最终与传统方法所得到的结果进行对比,如图7 所示。传统方法在工作温度阶段绝对最大误差和标准偏差(Std)分别为0.022 mm和0.009 3 mm,而采用自标定后其绝对最大误差和标准偏差(Std)分别为0.016 mm和0.005 6 mm,证明了本文所提出的自标定算法可以有效提升测量结果的稳定性。
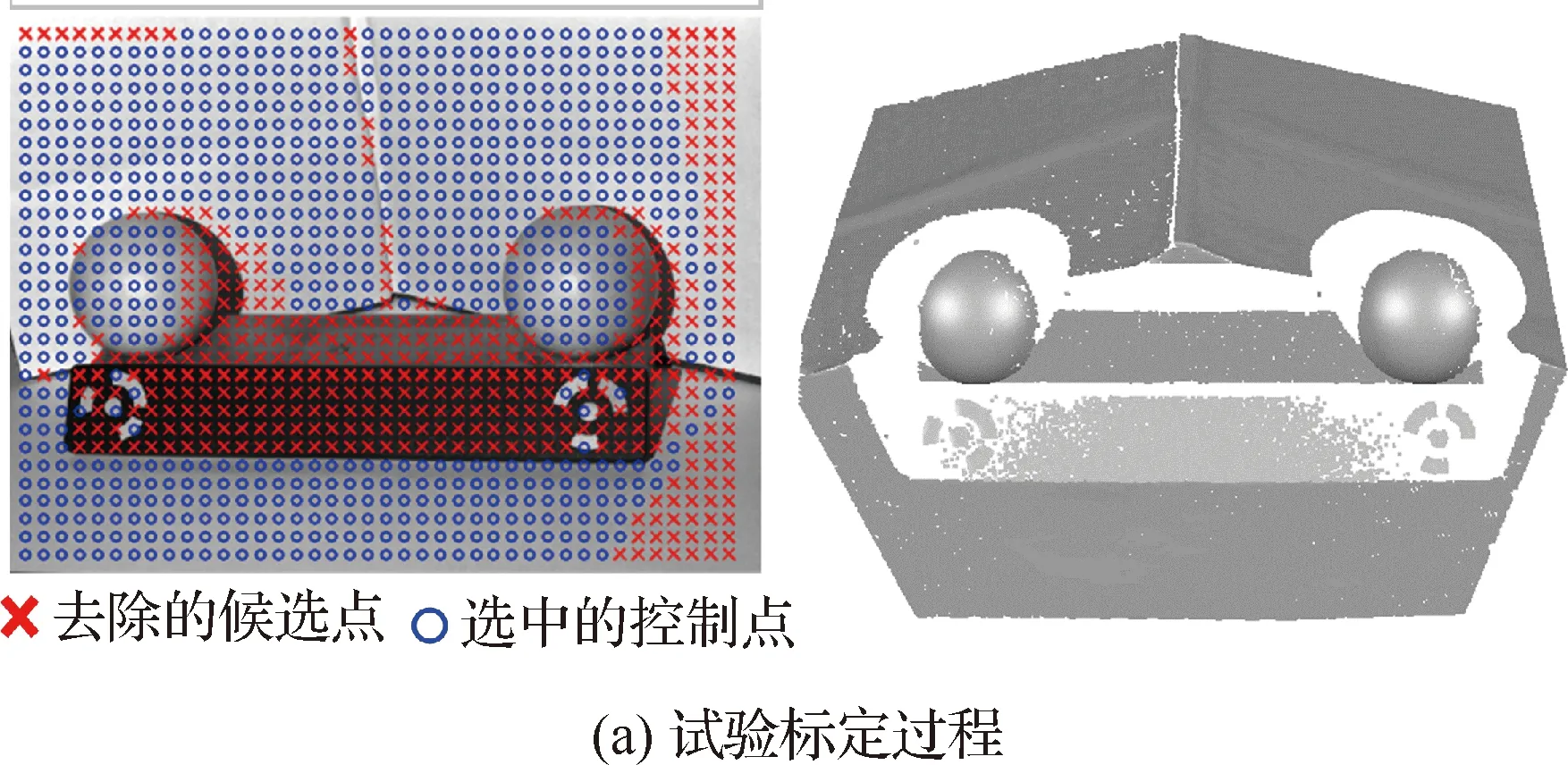
图7 自标定试验结果Fig.7 Self-calibration test results
1.3 基于全局优化的多视测量数据拼接方法
采用面结构光技术进行三维测量时,单个视角所获取的只是局部三维数据,需对多个视角的局部三维数据进行拼接配准以获得被测物体完整三维形貌。为保证测量精度,工业现场中最常用的拼接配准方法为标志点拼接法,但其过程繁琐、效率低,且难以适用于高温模锻件在线测量等领域。
为此,本文提出了一种基于位姿图全局优化的点云配准方法,针对具有显著特征的零件进行多视测量数据拼接,对标志点拼接法进行补充。首先依据曲率[32, 44-45]和几何形状一致性原则,采用深度图进行快速配准,实现相邻视点的初始位姿预估;然后结合初始位姿,对关键帧[46-47]进行回环检测[48-52],构建基于位姿图的全局多视点云优化模型以进行全局点云配准。
深度图配准方法主要依靠相机的正逆投影模型,根据相机参数,先采用逆向投影模型计算源深度图像上的点三维坐标(源相机坐标系),再根据源相机与目标相机的刚性变换矩阵(初始设为I),计算出三维点在目标相机坐标系下的坐标,继而求出目标深度图像上的对应点坐标。当源深度图像与目标图像上的像素点匹配后,相应的三维点也进行了匹配。此外,采用深度缓冲技术,当源图像中有多个点匹配到目标深度图像上同一点时,选取重建深度最小的像素点作为对应点。对应点计算完成之后,通过迭代方式计算出刚性变换矩阵。每一次迭代过程中,以上一次迭代计算出的矩阵作为结果进行深度图快速配准,再采用点到面距离衡量的方式构建误差方程,对相对位姿增量进行优化。误差方程为
Ereg=Egeo+λEcur
(15)
式中:Egeo为几何形状误差;Ecur为平均曲率误差;λ为比例因子。几何形状误差方程定义为
(16)
pi-1(x)′=ΔTi-1,iTi-1,ipi(x)
(17)
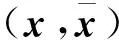
(18)
(19)
(20)
(21)
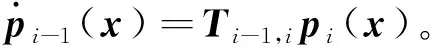
同理,根据图像扭曲的方式构建平均曲率误差模型,表示为
(22)
(23)
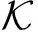
Ecur≈
(24)
(25)
(26)
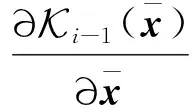
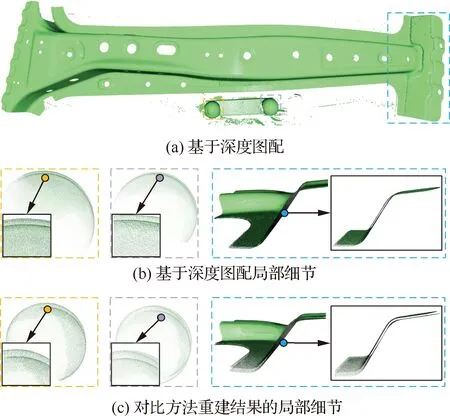
图8 三维重建结果对比Fig.8 Comparison of 3D reconstruction results
相对位姿计算完成之后,为可采用回环检测方式在位姿图框架下进行全局优化消除累计误差。采用深度配准时相邻位姿差别不能过大,因此对较大物体进行测量时最终帧数可能达几百。为加快速度提高效率,可先检测出关键帧,然后在关键帧之间进行回环检测,构建全局位姿约束关系。本文采用空间位姿距离作为标准对关键帧进行选取,遍历所有视点,当当前帧与上一个关键帧间的旋转距离或平移距离达到设定阈值时,即将当前帧作为关键帧。旋转距离与平移距离分别定义为
(27)
(28)
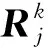
(29)
根据相对位姿以及相机投影模型,即可计算出两帧间深度图像的对应点数目(对应点需满足有效深度),再根据关键帧有效深度点总数,即可算出重叠比例。若重叠比例达到预设阈值,则进行重叠距离计算。重叠距离可根据对应点间的平均绝对误差进行计算
(30)
式中:N为对应点总数。
回环检测完成之后,可据此与相邻位姿关系构建全局优化模型。常用的方法一般为直接优化或位姿优化,对所有点云中的对应点的绝对误差进行优化:
(31)
式中:pw、qw分别为对应帧中对应三维点的世界坐标;nqw为qw的法向量。直接优化法虽然思路简单,但由于测量点云规模巨大,会导致全局优化缓慢甚至无法收敛的问题。位姿图优化法则是将全局位姿视为图节点,相邻局部位姿视为有向边,忽略对应三维点的距离关系,构建全局位姿与相邻局部位姿间的误差模型。
Ep-g(T)=∑e(Ti,Tj,Ti,j)Te(Ti,Tj,Ti,j)
(32)
式中:e(Ti,Tj,Ti,j)为i、j之间的绝对位姿与相对位姿的误差。误差方程可转换为李代数,再利用扰动模型根据非线性最小二乘法进行迭代优化,然后不断更新扰动项,最终获得优化的全局位姿。这种方法计算简单,但没有考虑对应点云的距离信息,难以保证最终点云拼接的精度。本文将这两种方法进行结合,构建出一种在位姿图框架下对多视点云的对应点距离绝对误差进行优化的方法,加快速度同时保证精度。几何形状距离函数为
(33)
考虑到刚性变换不影响对应点距离,且深度图点云配准帧间精度已经很高,因此可将式(33)近似变换为
(34)
运用扰动模型变换可得
(35)
将[-[pi]×I]定义为Gi,
(36)
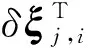
为验证多视测量数据拼接方法的准确性,如图9所示,采用基于全局优化的多视测量数据拼接方法对多个视角点云进行全局拼接。如表1所示,对全局拼接后所得到的标准球点云进行曲面拟合,得到标准球直径尺寸与球心距离,再和对应参考值进行比对分析误差。
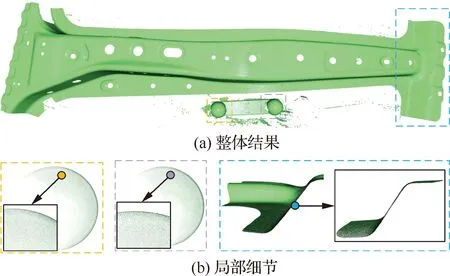
图9 全局优化结果Fig.9 Optimization results
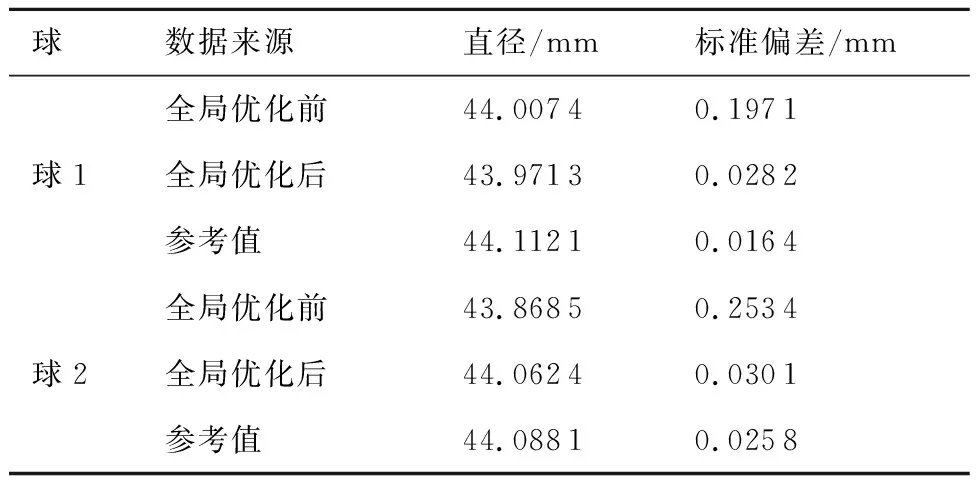
表1 标准球规试验结果Table 1 Standard ball gauge test results
1.4 基于自适应阈值ICP的点云背景噪声去除算法
在工业现场进行实际测量时,受生产线、工装夹具等复杂背景影响,最终得到的融合点云中会存在大量与被测工件无关的背景噪声数据,严重影响后续的数据分析处理等工作。
为此,本文以对应点间的欧式距离为依据,开发出一种基于自适应距离阈值ICP的背景去除算法。首先根据预标定位姿实现点云与CAD模型的初始粗配准,然后以测量点云与CAD模型之间的对应点距离为标准计算出每次迭代的距离阈值,不断迭代,最终实现点云与CAD模型的精配准,去除所有点云背景噪声。
生产线上的工件进行测量时一般不会进行刚性固定,因此同一批次不同工件所测量的点云数据在同一坐标系下位姿会有所不同。若采用固定距离作为阈值删除点云背景噪声,则极易导致点云背景噪声删除不全或误删有效数据。因此,本文采取由远及近的删除策略,将融合点云按照预标定的位姿转换到标定板坐标系下,同时将CAD模型预先放置在标定板坐标系下与其对齐。尽管每次测量时工件位姿会有一定偏差,但仍可实现测量点云与CAD模型的初始粗配准,为后续ICP精配准奠定基础。
实际生产过程中每次测量时工件位姿会发生偏移,采用传统的固定阈值距离ICP[53-55]算法容易导致误匹配的发生,因此本文以测量点云与CAD模型之间的对应点距离为标准,计算出每次迭代的自适应距离阈值,进行求解计算。设测量点云为P,模型点云为Q,以点到面的距离为标准进行点云配准,则公式为
(37)
式中:Nc为对应点总数目;ni为qi的法向量。
首先将测量点云根据预标定的位姿转换到标定板坐标系下,与CAD模型进行粗配准。然后以CAD模型点云上的所有点构建kd_tree,再遍历测量点云P中的所有点,根据CAD模型中构建好的kd_tree进行最近邻点搜索,构建匹配点对Ci。再依据匹配点对之间的欧式距离计算出此次迭代的距离阈值,计算公式为
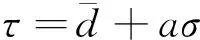
(38)
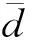
R=Rz(γ)Ry(β)Rx(α)=
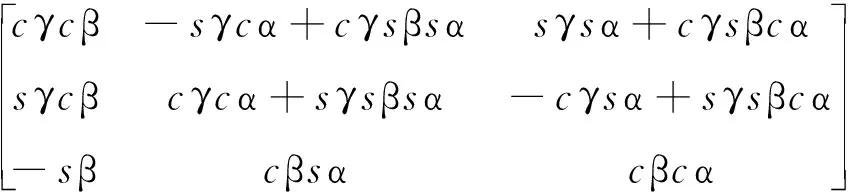
(39)
式中:c为cos;s为sin。设γ、β、α接近于0,则可将式(39)转换为
F(R,T)=F(α,β,γ,tx,ty,tz)≈
argmin(AB-C)2
(40)
(41)
(42)
(43)
B中的各个参数可以通过奇异值分解(Singular Value Decomposition,SVD)分解进行计算,从而获取旋转平移矩阵。不断迭代,直到满足迭代次数或达到收敛条件即可停止。
每次迭代可以去除部分点云背景噪声,当测量点云与CAD模型完全配准之后,即可根据距离将所有的点云背景噪声去除。图10为带有背景数据的转向节和外壳的迭代配准试验结果,尽管存在大量点云背景噪声,依然可迭代去除,最终与CAD模型进行精确配准。
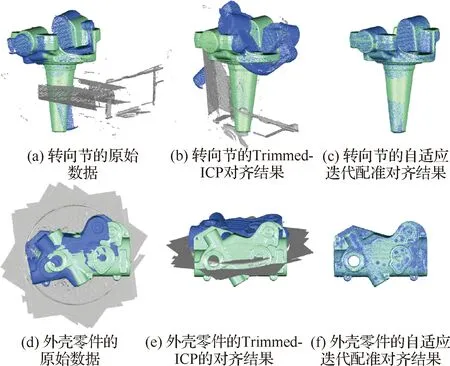
图10 数据配准实验结果Fig.10 Data alignment experiment results
2 装备研制
在第1节所述关键技术的研究基础上,本课题组开发出了基于面结构光的复杂零件机器人自动化三维测量装备。如图11所示,将面结构光三维测量设备安装在六自由度机器人上,配合高精度转台、导轨等运动装置,实现复杂零件的自动化三维测量和精度检测。测量前采用PowerVirtualPlan视点规划软件合理规划出测量视点,生成测量路径;测量时采用PowerScan三维测量软件控制机器人带动测头运动到规划的测量视点位置,依次对被测复杂零件进行三维测量,得到零件的三维数据;最后使用iPoint3D软件处理上一步得到的三维测量数据,对复杂零件的制造精度进行自动分析和检测。
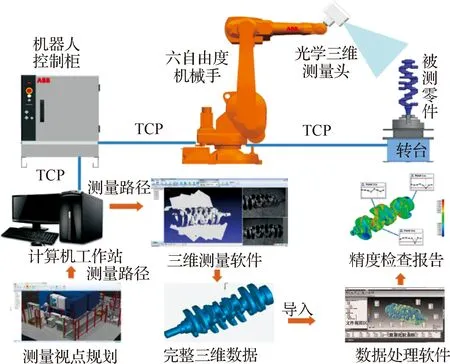
图11 基于面结构光的复杂零件机器人自动化三维测量技术原理图Fig.11 Schematic diagram of robot automated 3D measurement technology for complex parts based on surface structured light
2.1 PowerVirtualPlan视点规划软件
PowerVirtualPlan视点规划软件的功能为自动生成三维测量视点及规划测量路径。用户导入待测工件模型,设置参数后可自动地实现视点生成和路径规划。由于最终的运动是通过机器人来完成,需进行模拟,因此本软件在Robotstudio环境下进行开发。软件主要包括功能界面、模型显示界面、视点管理界面、信息输出界面等,如图12所示。
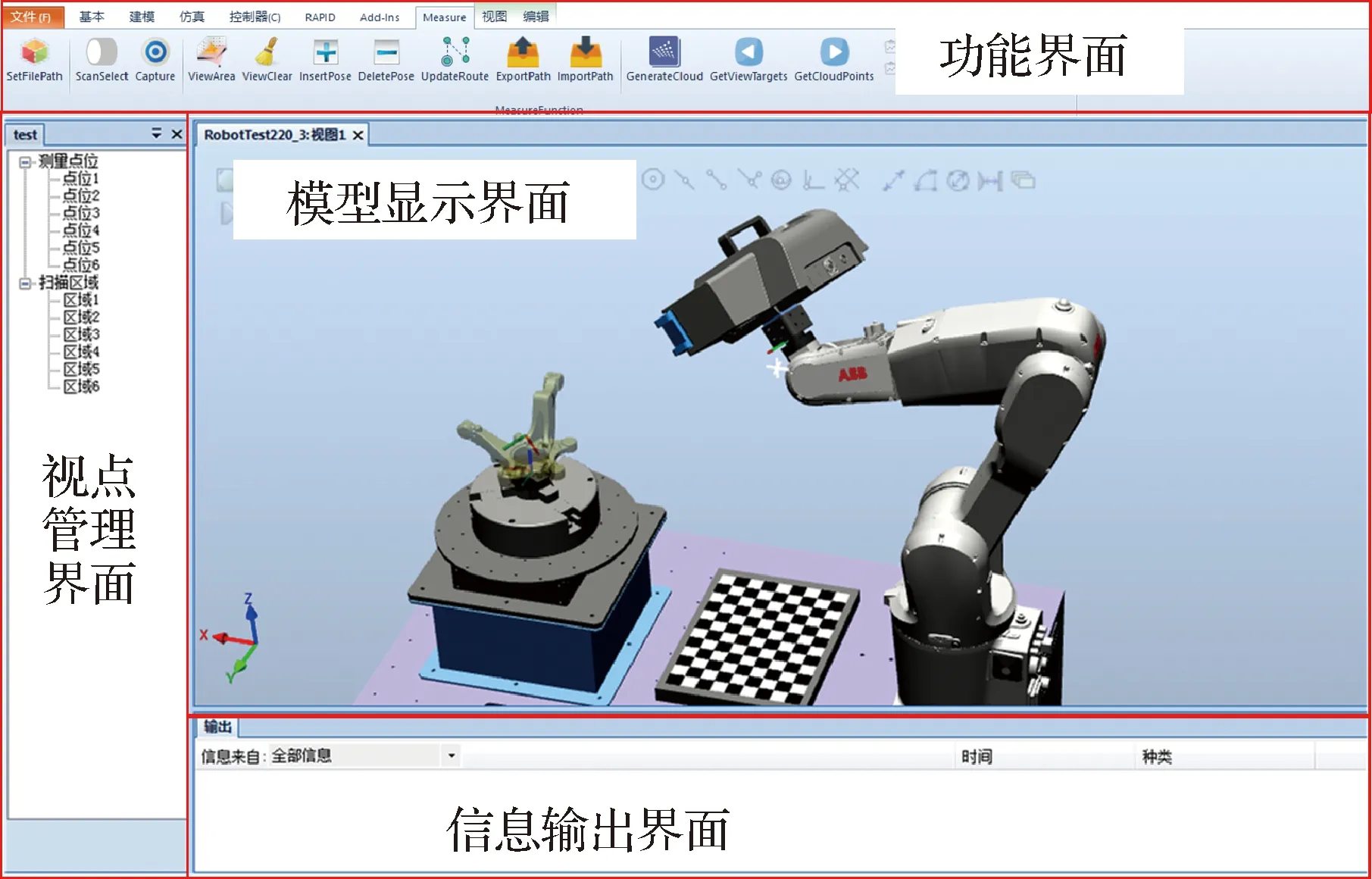
图12 PowerVirtualPlan 视点规划软件界面图Fig.12 Interface diagram of PowerVirtualPlan viewpoint planning software
功能界面主要显示软件可实现的功能,包括添加扫描模型、导入导出测量视点等;模型显示界面用于显示导入的机器人、测量设备和测量零件模型,在此界面可以自由拖动、缩放、移动、选择模型,以及点击零件表面选择想要测量的区域手动生成测量视点;视点管理界面生成测量视点工程树,对视点进行查看和管理;信息输出界面用来查看系统反馈的信息,会显示进行的操作成功或者失败,给出相应提示。比如判断机器人能否到达生成的视点,若不能则会提示“无法到达该视点”。
2.2 PowerScan三维测量软件
PowerScan三维测量软件主要是将结构光三维重建、系统参数自标定、多视测量数据拼接等自动化三维测量核心技术进行集成,同时添加与机器人、转台等的交互功能,实现自动化三维测量。如图13所示,PowerScan界面主要分为4个部分,分别是自动化三维测量控制界面、工程界面、点云显示界面和相机显示界面。其中,自动化三维测量控制界面主要负责整个软件的操作部分,包括整个软件的命令按钮,进行前端界面与后端算法的交互。工程界面、点云显示界面和相机显示界面则主要是显示一些文件以及图像、点云等数据,实现测量结果实时显示。
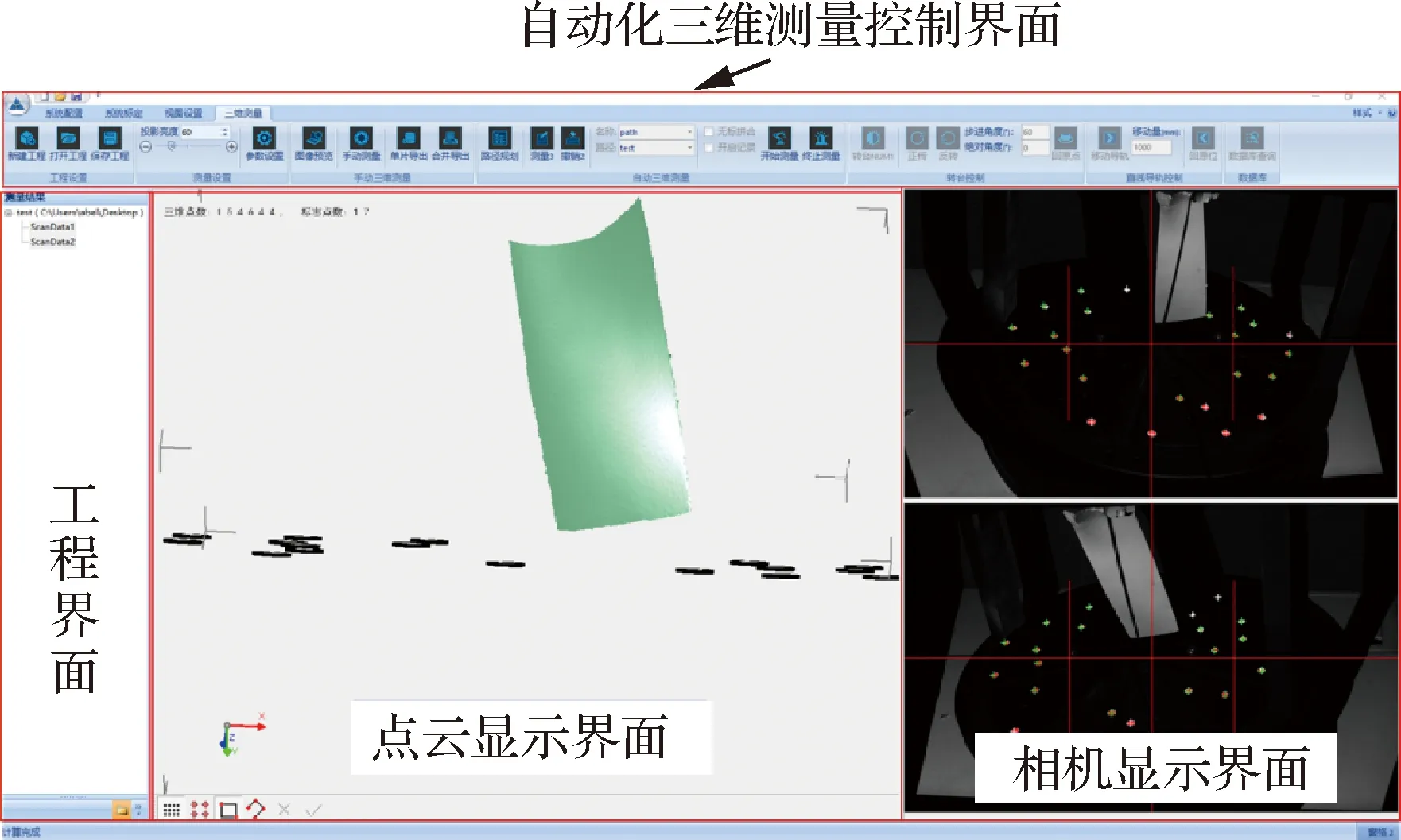
图13 PowerScan 三维测量软件界面图Fig.13 Interface diagram of PowerScan 3D measurement software
除此之外,为提高工业现场测量的速度,本课题组基于全流水线与前端并行的设计原则,提出一套基于FPGA平台的三维重建算法架构,完成了相位计算、相位展开、相位矫正、相位匹配、三维重建等多个模块的全新构建。相较传统的CPU计算架构[56-59]而言,测量精度基本一致,加速倍数可提高100倍以上。
2.3 iPoint3D数据处理软件
如图14所示,iPoint3D数据处理软件的主要功能是对最终测量得到的点云数据进行分析处理,分为通用模块与专用模块两个部分。通用模块主要包括常用的点云精简、光顺、模型匹配、报告生成等基本功能。专用模块则主要是针对特定场景,根据工业现场实际需求进行定制开发,目前已经有锻造曲轴检测、飞机蒙皮修边测量等专用功能[9]。
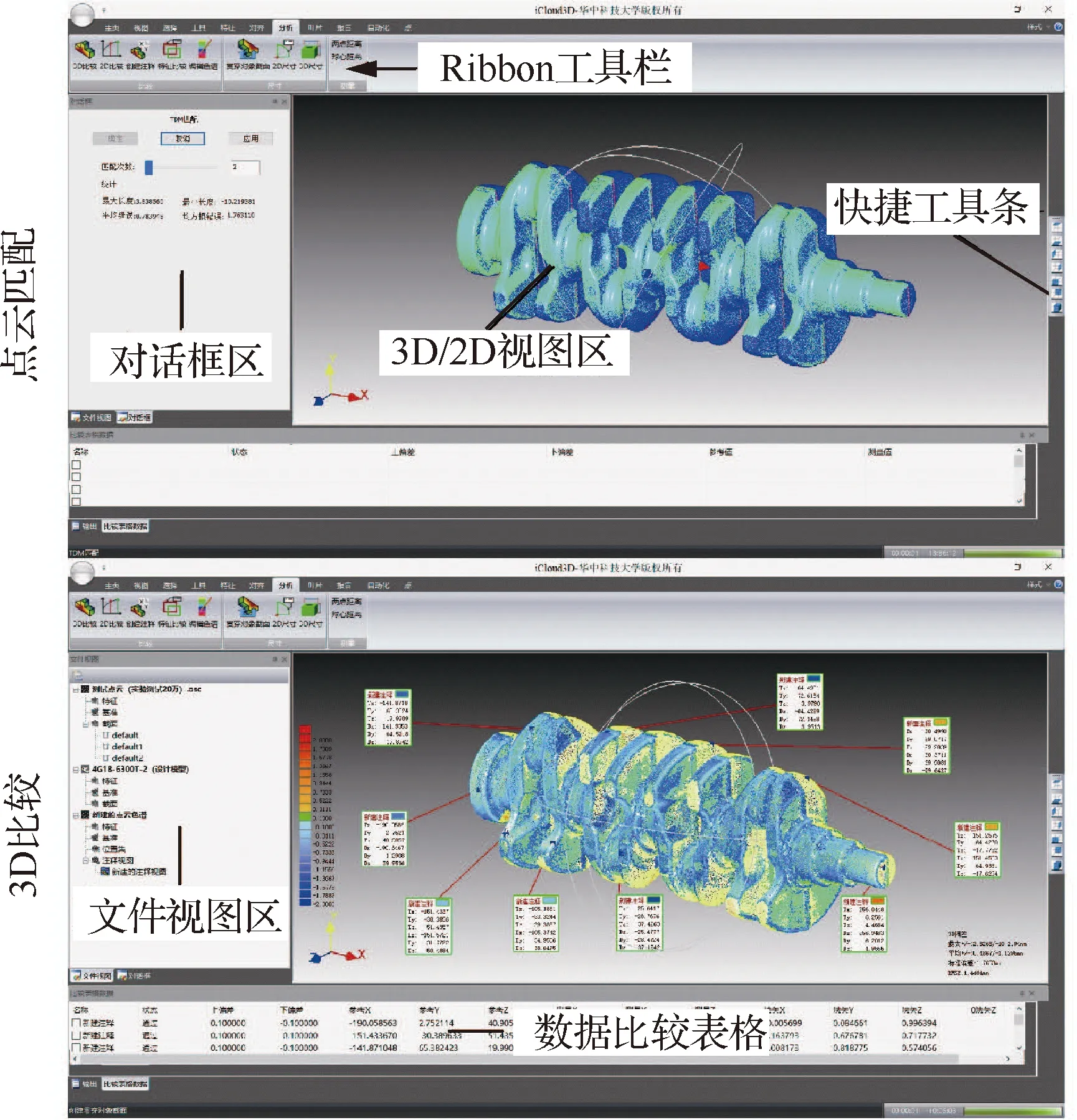
图14 iPoint3D 数据处理软件界面图Fig.14 Interface diagram of iPoint3D data processing software
2.4 系列装备研制
在上述3个软件的基础上,本课题组开发了AutoScan系列工业自动化三维测量装备,具备自动测量、自动拼接、自动分析、实时监控、定制化开发等功能,可用于产品生产过程中的首末件检测、线边抽检、线上全检,即刻判定产品是否合格并自动分拣,已通过惟景三维科技有限公司[60]进行产业化应用。图15所示分别为AutoScan1000、AutoScan2000与AutoScan-H这3种不同型号的自动化三维测量设备,可应用于单批次生产过程中,对首件及末件零件进行检测,帮助产品工序质量控制,用于预防机床、模具等部件受损导致的成批超差、返修、报废等情况,也可对多批次生产过程中的数据进行储存与管理,帮助优化工艺参数,提高零件加工精度,推动智能制造的发展进程。其中,AutoScan1000与AutoScan2000用于常温工件三维测量,搭载PowerScan系列常温三维测头。如图16(a) 所示,单次测量时间为0.4 s,单次测量范围可达430 mm×280 mm,单次测量精度最高可达±0.015 mm, 满足大部分工业生产的实际应用需求。AutoScan-H用于高温锻件三维测量,搭载PowerScan-H系列高温测头。如图16(b)所示,单次测量时间为0.4 s,单次测量范围可达430 mm×280 mm,单次测量精度最高可达±0.015 mm, 主要应用于高温物体测量,能够消除高温物体辐射对图像采集质量的影响,同时保证设备运行的稳定性,测量物体最高温度可到1 100 ℃。

图15 Autoscan系列自动化三维测量装备Fig.15 Automated 3D measurement equipment of Autoscan series

图16 PowerScan 系列蓝光面扫描三维测头Fig.16 Blue surface scanning 3D probe of PowerScan series
3 自动化三维测量工程应用
3.1 航空发动机机匣精度检测
航空发动机是飞机的核心部件,决定飞机的性能及使用寿命。发动机机匣作为整个发动机的基座,是发动机中最关键的承力部位,决定发动机的可靠性。发动机机匣形状复杂且壁薄(弱刚性零件),在加工过程中极易产生变形,导致最终加工精度低。为保证飞机的安全性能,使用发动机前需对发动机机匣的尺寸进行检测。传统方法一般采用三坐标测量机等对机匣进行检测,但受机匣复杂形状影响,难以获取机匣内部关键部位的几何尺寸。
本课题组与某航空发动机零件制造企业合作,首先采用PowerVirtualPlan视点规划软件对发动机机匣的CAD模型进行视点规划,生成最优测量路径并导出;然后采用PowerScan三维测量软件导入测量路径,控制AutoScan自动化三维测量设备在预规划的多个视点位置对航空发动机机匣进行检测,重建出机匣内外的整体三维点云并去除背景数据,整体测量时间为3~5 min,整体测量精度可达0.05 mm,如图17所示;最后可预先设定好模板,采用iPoint3D数据处理软件对重建的三维点云进行分析,检测机匣关键部位的尺寸,如图18所示。

图17 航空发动机机匣检测Fig.17 Aeroengine casing inspection scene
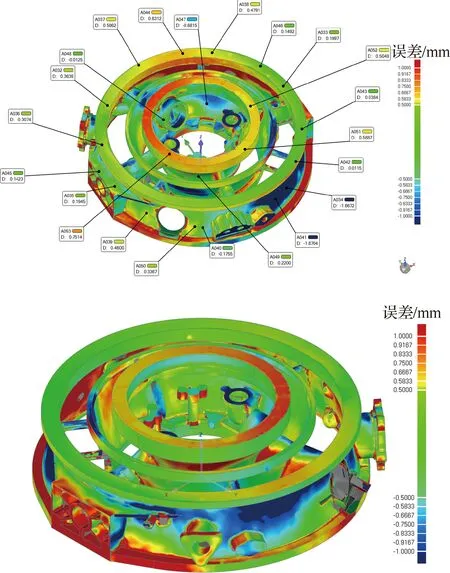
图18 机匣误差分析结果Fig.18 Result of error analysis of casing
3.2 航天用箱体精度检测及余量分析
箱体类铸件是航空、航天领域中的通用零件,结构复杂,加工精度要求高,加工之前需进行余量分布的检测。如图19所示,目前主要采用人工划线的方式进行余量分析,在检测平台上使用钩针和卡尺在铸件表面划出尺寸线,用以指导后续机加工,存在尺寸基准不统一、尺寸超差判定不准确、尺寸检测效率低等突出问题。

图19 人工划线Fig.19 Manual marking scene
本课题组与某军工单位合作,采用课题组自主研制的AutoScan自动化三维测量设备,对箱体类铸件进行了自动化三维测量,可自动完成多种航天用箱体类铸件自动化三维测量和精度检测,并根据测量结果自动进行余量分析,保证后续加工精度。
如图20所示,采用自动化三维测量设备获取到铸件完整的三维数据后(精度高于0.1 mm),数据分析软件将自动把测量数据和模型数据按照既定的方式进行对齐,以分析各加工面的加工余量,给出报告结果,实现铸件加工余量的快速测量,判断铸件是否合格。再根据报告结果,在数据处理软件中调整测量数据在x、y和z这3个方向的平移,使余量分布满足加工要求,如图21所示。
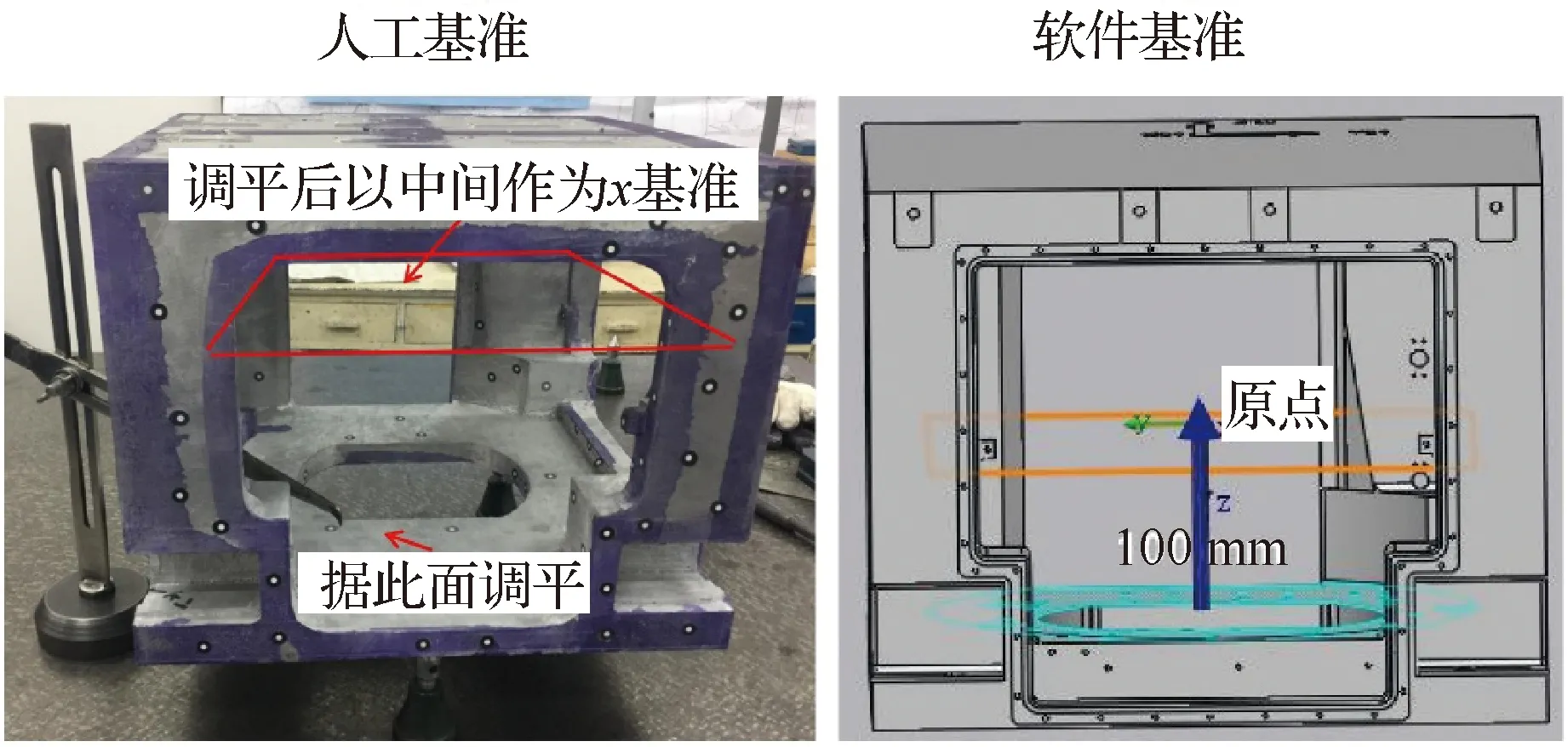
图20 测量数据与模型对齐Fig.20 Alignment of measurement data and model
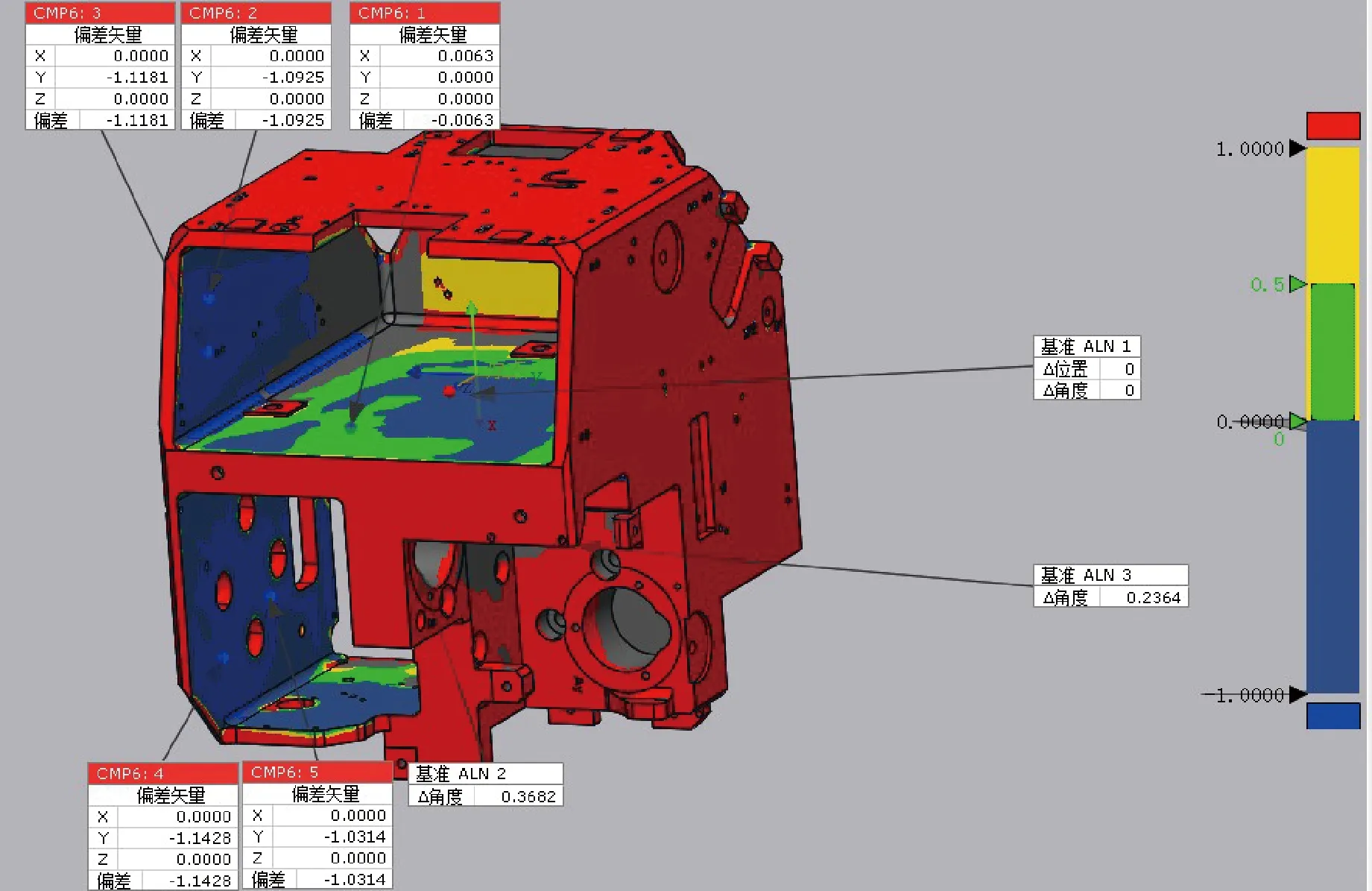
图21 加工余量分析结果Fig.21 Result of machining allowance analysis
3.3 高温模锻件测量
锻件是高端装备的关键承力部位,决定装备的安全性能。当前,汽车前桥等高温锻件多依靠三坐标测量仪或专用夹具检具进行检测,只能实现锻件的最终检测,无法在锻造过程中对零件的关键尺寸进行测量,难以满足生产制造的需求。现有的结构光三维测量技术虽然可以对普通零件进行实时检测,但对于振动工况下的高温锻件仍然无法实现稳定的高精度测量,难以实际应用。本课题组与某汽车车桥锻件生产企业合作,实现了高温、振动等复杂工况下的高温前桥锻件自动化三维测量。与传统方法相比,节约了人力成本,提高了生产效率。
图22为汽车前桥锻件生产线检测实景,采用机器人将生产线上的高温红热锻件放置在检测区域直接进行检测,然后根据检测结果运往相应的后续流程。检测过程中,锻件的温度在750~900 ℃ 之间,测量时间为28 s,精度可达0.15 mm。测量完成之后,如图23所示,采用数据分析软件将测量点云与CAD模型配准,对左右瓜头、钢板等关键部位的尺寸进行分析,判断锻件是否合格,实现废品的自动化分拣。如图24所示,还可对生产线上的锻件尺寸生产趋势进行分析,为之后 的锻造生产工艺优化提供基础数据。
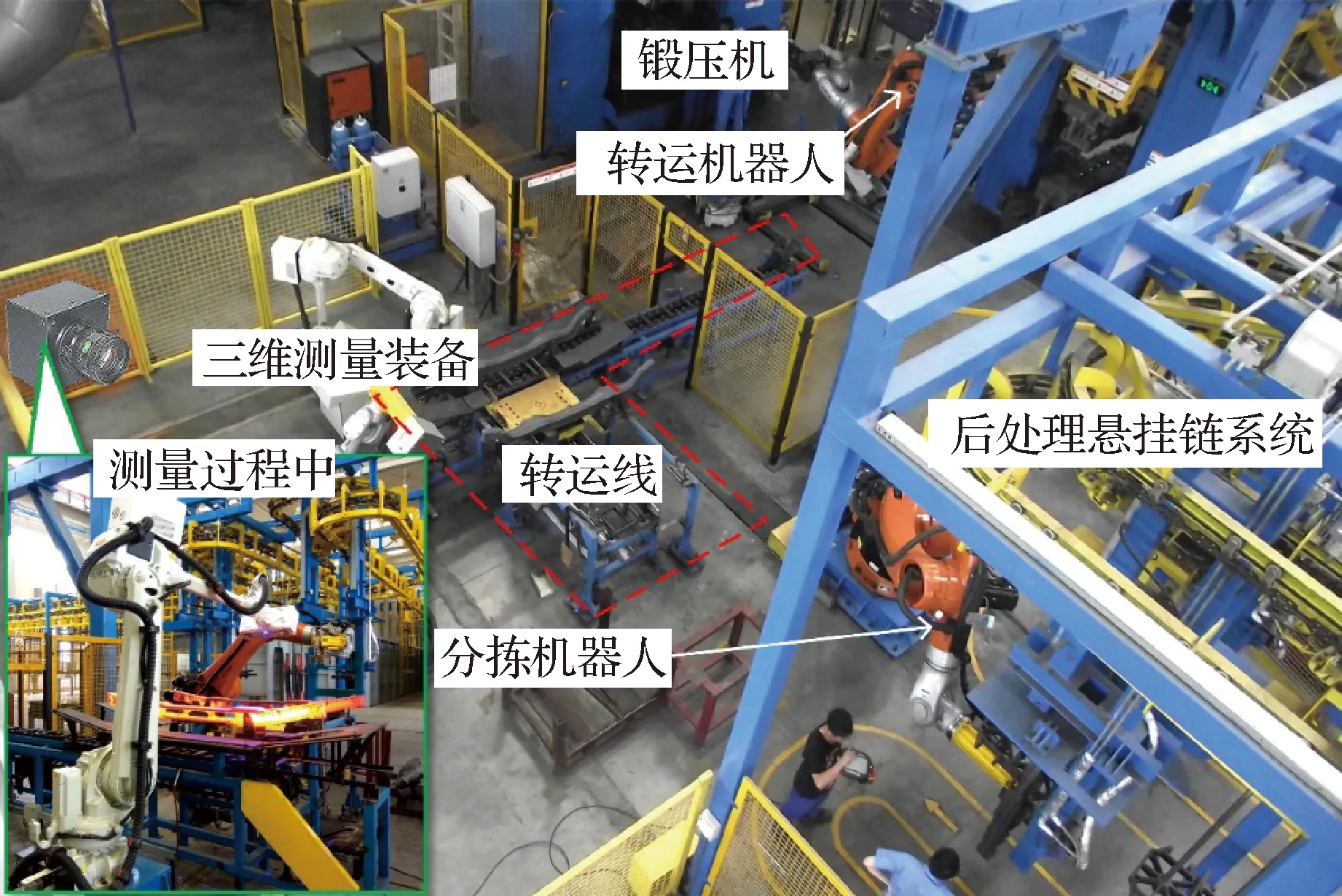
图22 高温锻件自动化三维测量现场Fig.22 Automated 3D measurement site for high temperature forgings
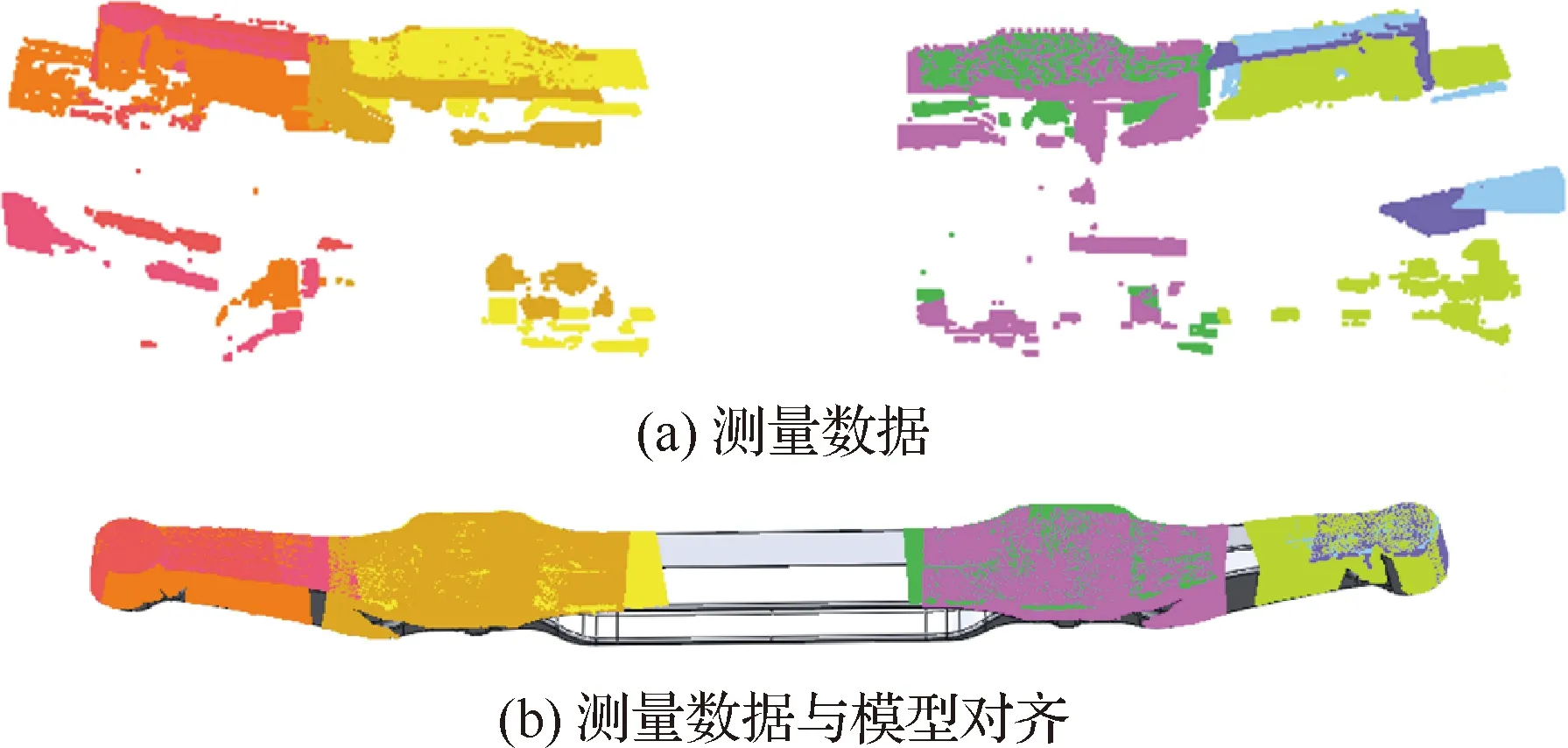
图23 测量点云与CAD 模型配准结果Fig.23 Registration result of measurement point cloud and CAD model
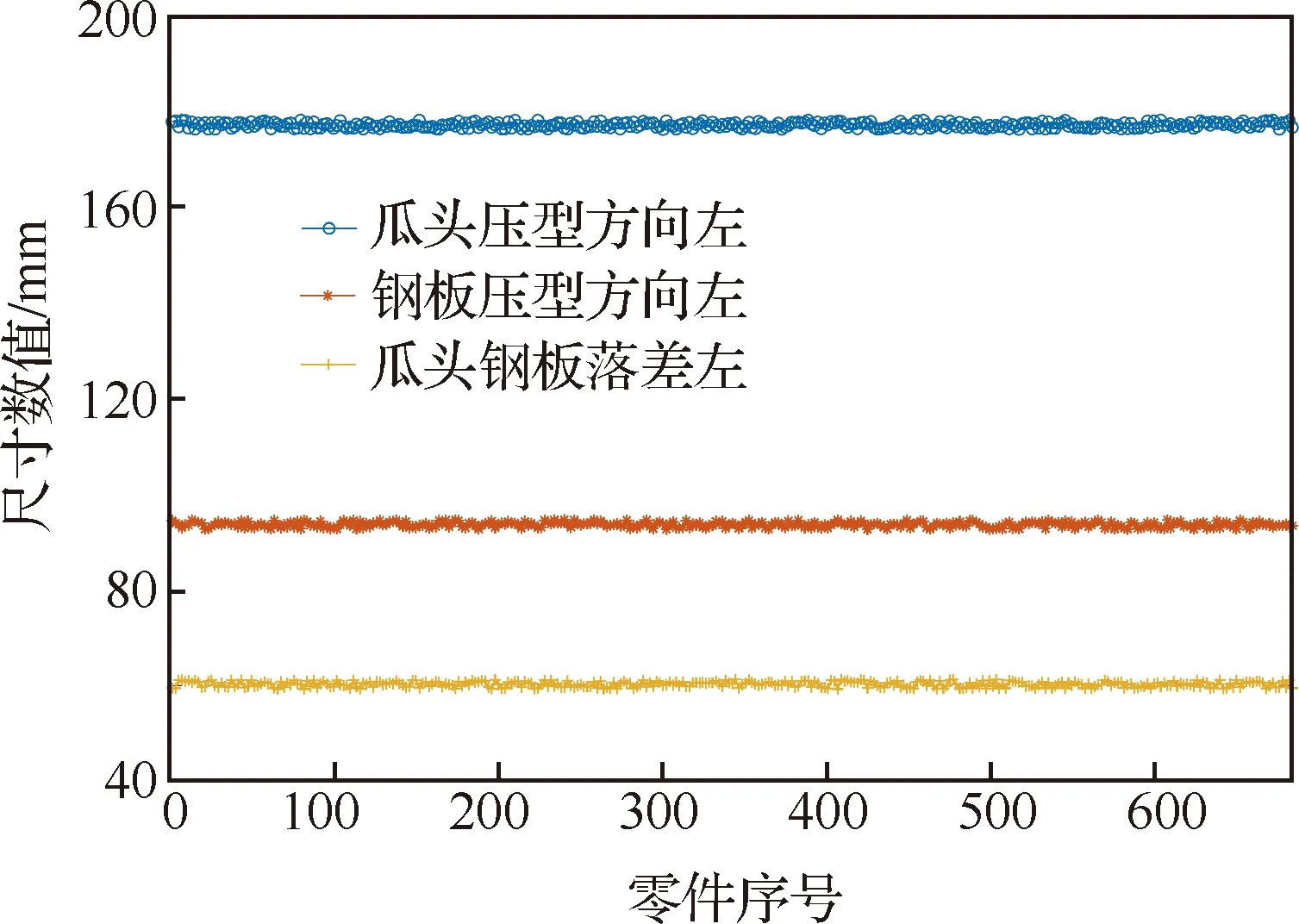
图24 锻件尺寸趋势分析结果Fig.24 Results of forging size trend analysis
4 结 论
基于面结构光的自动化三维测量技术是实现自动化三维测量的主流技术之一,在工业零件检测方面有着良好的应用前景。本文针对其应用中存在的视点规划效率低、离线标定过程繁琐、多视测量数据拼接精度低、数据自动处理稳定性差等问题,详细介绍了基于双目测头的测量视点规划、基于耦合焦距比例约束的参数自标定、基于多视图全局位姿优化的多视点云拼接、基于自适应阈值ICP的点云背景噪声数据去除等关键技术,以及基于这些技术的设备开发与应用。
基于面结构光的复杂零件自动化三维测量技术的发展趋势如下:
1) 随着技术的不断发展,对于零件的制造精度要求越来越高,相应的对于三维测量的精度要求也越来越高。因此,需要在相机参数标定、三维重建、多视点云数据拼接等方面继续改进,以实现更高的测量精度。
2) 现有的自动化三维测量设备在室内等稳定环境中可以实现较好的测量效果,但当处于阳光、高温、振动等复杂环境时,难以保证测量精度的稳定性。因此,需要在相机硬件与算法等方面进行改进,增强三维测量设备的适用性,保证其在各种环境中实现稳定测量。
3) 智能化的制造业应该根据生产过程中被加工工件的实际状况,实时修正程序,并调整生产工艺。当前自动化三维测量设备可以根据重建的三维数据对被测工件的实际状况进行分析,但难以直接给出工艺优化措施,仍需人工去进一步分析。因此,需要加强基于测量数据的工艺优化,对生产过程中的工艺参数进行自动调控,实现信息化和工业化的融合,推进生产制造过程的全智能化发展。

