基于径向基函数神经网络的地震液化侧移预测
范珂显 李 恒,2 张 祎,2
1 中国地震局地震大地测量重点实验室,武汉市洪山侧路40号,4300712 武汉地震工程研究院有限公司,武汉市洪山侧路40号,430071
侧移是液化区房屋、地下结构与公路、铁路、桥梁等生命线工程最主要的震害形式,其广泛性可与液化地基失效相比,而后果的严重性则过之。目前,液化侧移的预测方法主要有以下几种:数值模拟、模型试验、基于震害数据的经验方法和机器学习算法。其中数值模拟和模型试验精度最高,但是适用范围有限、成本高,不适合工程实践推广。基于震害数据的经验方法使用方便、适用范围广,易满足工程需求[1-9]。对于该方法,虽然前人提出的数学公式简明、输入变量和输出之间关系明确,但同时精度和适用性受到固定公式的限制。
为了更加准确、有效地预测场地液化侧移程度,本文考虑到震源机制的影响,在已有的震害调查数据中新增Kramer等[10]所提出的累积绝对速度(cumulative absolute velocity after application of 5 cm/s2threshold acceleration,CAV5)参数,并采用精度高、易训练的径向基函数神经网络(radial basis function neural network,RBFNN)对液化侧移进行预测。
1 数据库选取
1.1 累积绝对速度
Reed等[11]首次将累积绝对速度(cumulative absolute velocity,CAV)作为评估结构损伤的标准,其公式为:
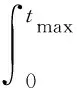
(1)
式中,a(t)为地震动加速度,t为时间,tmax为地震持续时间。
Kramer等[10]研究发现,小于5 cm/s2的地震加速度对孔隙水压力的贡献极小,因此提出大于5 cm/s2地震动加速度绝对值积分CAV5:
(2)
同时,Kramer等[10]利用太平洋强震工程研究(PEER)数据库提出计算浅层地壳地震的CAV5的衰减公式:
lnCAV5=3.495+2.764(M-6)-
0.464FN+0.165FR
(3)
式中,M为矩震级,r为震中距(km)。对于走滑断层,FN=FR=0;对于正断层,FN=1,FR=0;对于逆断层,FN=0,FR=1。该公式适用震级为6.4~7.9级,震中距范围为100 km以内。
1.2 数据整理
本文采用的数据库为文献[12-13]建立的有关液化侧移及其影响因素的历史数据库,总共有476个历史数据,主要来自中国、日本、美国等地的多次地震数据记录。考虑到地震的发震断层类型对地震液化的影响,因此使用式(3)估计CAV5,并将其加入数据库中进行分析。为了满足式(3)的使用条件,从已有数据库中剔除1906年旧金山7.9级、1964年阿拉斯加9.2级地震等11条数据,最终数据库如表1所示。
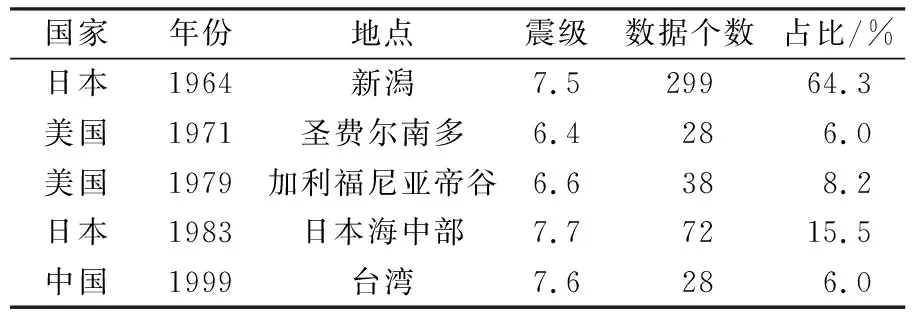
表1 液化侧移数据库
该数据库中包含226条临空情况(河岸、水渠、挡土墙等在地震中由于液化使整个土体向河或海中侧移)记录,239条缓坡情况(倾斜场地由于液化使液化土层以及上覆土层沿坡面整体滑移)记录。随机选取372组(80%)数据作为训练组,剩余93组(20%)数据作为测试组,各组参数范围如表2所示。

表2 数据库中的参数及其取值范围
2 RBFNN原理
典型的RBFNN由输入层、隐含层、输出层组成,其结构如图1所示。其中,输入层由输入矩阵的原节点组成;第2层为隐含层,由一组径向基函数构成,一般选择高斯函数作为径向基函数;隐含层的输出按权值叠加,得到RBF网络的输出。
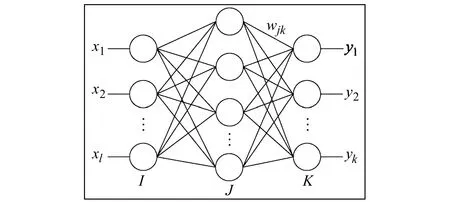
图1 RBFNN结构示意图Fig.1 Structure diagram of RBFNN
径向基函数神经网络的优点有:能够逼近任意的非线性函数,可以处理系统内难以解析的规律性,适合处理液化侧移这种非线性映射问题;具有良好的泛化能力,对不同场地环境均能起到预测作用;有很快的学习收敛速度,可以随着数据库的更新随时对网络进行训练更新。
3 预测模型建立
本文采用MATLAB 2019A中的神经网络通用函数newrb(P,T,Goal,Spread,MN,DF)来建立预测模型,其中P为输入矩阵,T为输出矩阵,Goal为均方误差的目标,Spread为径向基的扩展速度,MN为最大的神经元个数(即神经元个数到MN后立即停止网络训练),DF为循环过程中每次加进来的神经元个数。模型的建立需要对newrb函数中Spread、MN参数进行择优选取,以避免过拟合或欠拟合。
为了调整参数达到最优效果,采用社会群体优化算法(social group optimization,SGO)[14]进行参数寻优。通过MATLAB将SGO算法进行编程,得到SGO-RBFNN模型,优化流程如图2所示,设置种群规模N=10,变量维数D=2。

图2 SGO-RBFNN模型优化流程Fig.2 Flow chart of SGO-RBFNN model
分别使用数据库原有的7项参数和将震级、震中距2项参数用累计绝对速度CAV5进行代替的6项参数进行训练。以均方根误差(RMSE)为目标进行优化,得到训练完毕的网络,对训练组和测试组地震液化侧移进行预测。
4 预测结果
4.1 误差分析
图3为使用SGO-RBFNN模型得到的预测结果,图4为用CAV5代替震级、震中距后使用SGO-RBFNN模型得到的预测结果。

图3 SGO-RBFNN模型预测结果Fig.3 Prediction results of SGO-RBFNN model
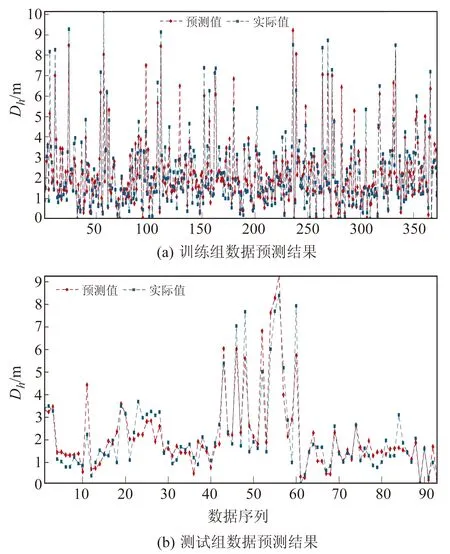
图4 SGO-RBFNN模型预测结果(CAV5)Fig.4 Prediction results of SGO-RBFNN model (CAV5)
采用决定系数R2、均方根误差RMSE以及平均绝对误差MAE评估模型性能。表3列出了上述2种模型与多元统计回归法(multiple linear regression,MLR)模型和遗传编程(genetic programming,GP)模型的各项指标的比较。可以看出,本文模型预测精度最高。这是因为地震参数CAV5较震级、震中距2项参数包含了更多的震源机制信息,因此可以在一定程度上提高预测的准确性。

表3 液化侧移预测效果对比
图5列出了MLR、GP、SGO-RBFNN模型的预测值与实际值的差异程度。可以看出,SGO-RBFNN模型的预测值基本在实际值0.5倍到2倍以内,而使用MLR和GP模型时,当实际侧移值在4 m以内会产生较大的预测误差。
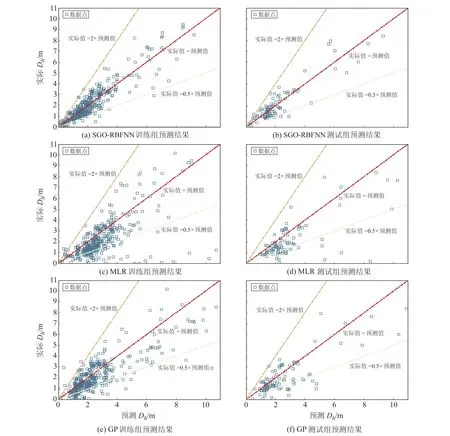
图5 液化侧移预测效果对比Fig.5 Comparison of prediction results of liquefaction-induced lateral spread
4.2 参数敏感性
为了对数据集中各项输入参数的重要性程度进行评估,将预测组数据的输入参数震级M、震中距R、可液化土层厚度T15、平均细粒土含量F15、平均粒径D5015、缓坡坡度S和临空面坡度W分别乘1.2和1.5的变化系数,然后再进行预测,所得到的性能评价指标见表4。
由表4可知,按照RMSE排序,参数震级M、震中距R、累计绝对速度CAV5、可液化土层厚度T15敏感性较高,对液化侧移影响程度较大;而参数平均粒径D5015、平均细粒土含量F15、临空面坡度W、缓坡坡度S对液化侧移影响较小。由此可见,地震因素对液化侧移影响最大,其次是土体因素和地质因素,场地因素对液化侧移影响较小。震级、震中距决定场地的地震动强弱,累积加速度表征地震动在整个地震过程中的累加效果,可液

表4 参数敏感性分析
化土层厚度决定场地的液化程度,因此,液化侧移程度更多地受地震、土体因素的影响。
5 结 语
本文基于已有的地震液化数据库和RBFNN方法,利用衰减公式引入地震参数CAV5,提出SGO-RBFNN地震液化侧移评估模型,经过试验得到以下结论:
1) SGO-RBFNN模型预测结果的决定系数R2、均方根误差RMSE以及平均绝对误差MAE均优于前人的模型,可以作为一种有效的地震液化侧移预测模型;
2)累积绝对速度CAV5包含震级、震中距以及断层类型的信息,可以有效替代震级和震中距对地震液化侧移进行预测;
3) 通过敏感性分析发现,对液化侧移预测较为明显的参数有震级M、震中距R、累积绝对速度CAV5、可液化土层厚度T15,而平均细粒土含量F15、平均粒径D5015、临空面坡度W、缓坡坡度S对液化侧移预测的影响较小。

