基于偏差改正的病态模型Liu估计的单位权方差无偏估计
丁斌芬 安洁玉
1 江西应用科技学院软件与区块链学院,南昌市联福大道1号,330100
当观测模型的系数阵呈良态时,最小二乘法能获得最优无偏的参数估值。然而,当模型的系数阵呈病态时,微小的观测误差会导致解的巨大波动,使常规最小二乘估计的解不可靠[1]。为此,学者们提出多种估计方法,如 Tikhonov 正则化、岭估计、截断奇异值分解(truncated singular value decomposition,TSVD)和Liu估计等[2-9]。目前关于病态模型的有偏性研究大都集中于Tikhonov正则化或TSVD 正则化[10-12],鲜有涉及Liu估计的相关研究。不同于Tikhonov 正则化,Liu 估计除含有正则化参数外,还额外引入了一个修正因子,因此可更加灵活地处理病态问题[7-9]。但由于引入了正则化参数和修正因子,Liu估计是有偏的。事实上,Liu估计正是通过牺牲参数估值的无偏性来换取其有效性。
基于以上研究,本文首先分析了由于引进正则化参数和修正因子而导致的Liu估计解及其残差的偏差;然后将偏差从残差中扣除,并利用偏差改正后的残差导出Liu估计的单位权方差估计公式;最后用数值算例和病态测边网算例验证公式的有效性。
1 病态模型及其Liu估计解法
测量上常用的Gauss-Markov模型为:
y=Ax+e
(1)
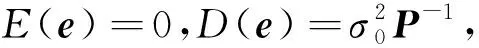
(2)
式中,N=ATA。当系数矩阵病态时,最小二乘解变得极不可靠。Liu[7]采用Liu估计解算病态模型参数,其在最小二乘准则的基础上额外增加了一个约束项,即
eTe+fTf=min
(3)
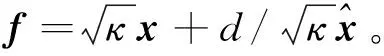
(4)
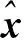
2 基于偏差改正的Liu估计的单位权方差估计
2.1 Liu估计的残差及其偏差
(5)
将式(5)代入式(1)中可得残差:
(6)
对式(6)两边取期望,得:
(7)
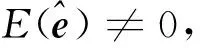
(8)
将式(8)代入式(1),可得残差为:
(9)
对式(9)取期望可得残差的偏差:
(10)
2.2 基于偏差改正的单位权方差估计
传统基于残差计算单位权方差的公式为:
(11)
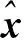
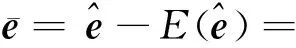
(12)

(13)
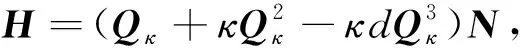
(14)
则方差阵的迹为:
(15)
由二次型的数学期望公式有:
(16)
(17)
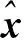
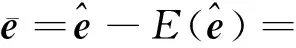
(18)
其方差为:
(19)
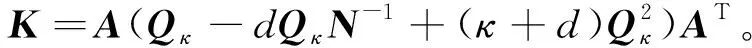
(20)
式中,
(21)
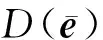
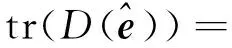
(22)
顾及式(16)可得单位权方差:
(23)
3 算例与分析
3.1 数值算例
Hilbert矩阵是一类典型的病态矩阵,假设A∈Rm×n为某一Hilbert矩阵,其元素构成为:
(24)
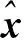
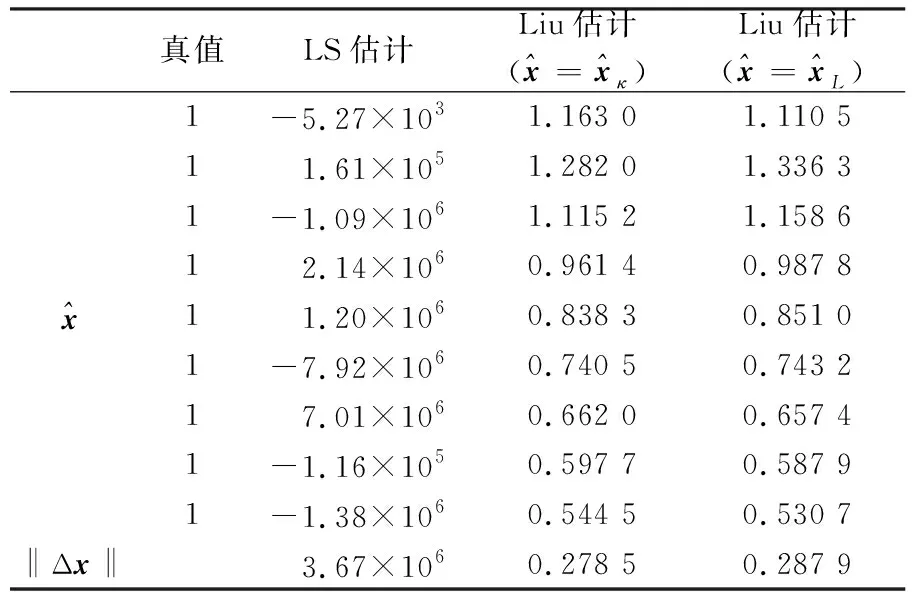
表1 σ0=0.1时不同算法解算的参数估值
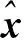
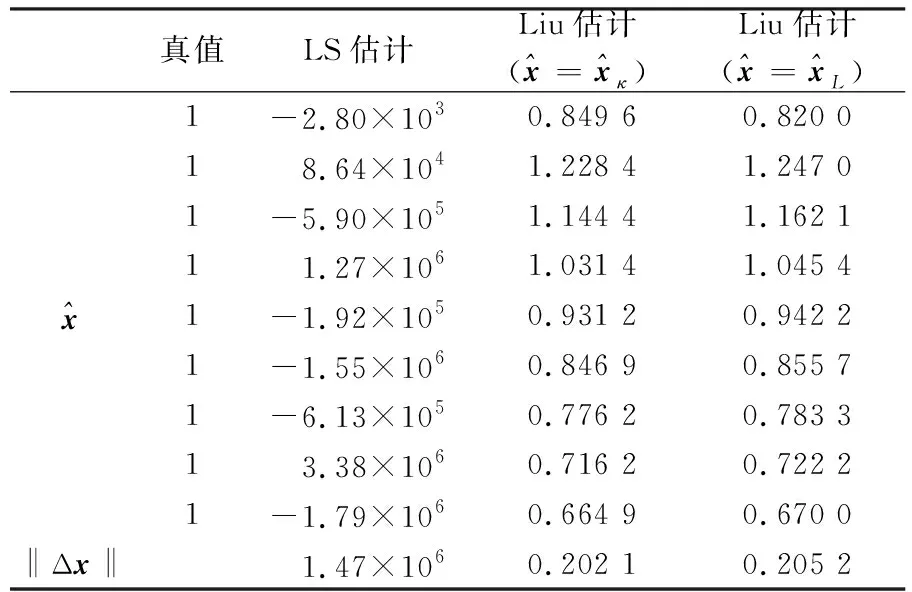
表2 σ0=0.01时不同算法解算的参数估值
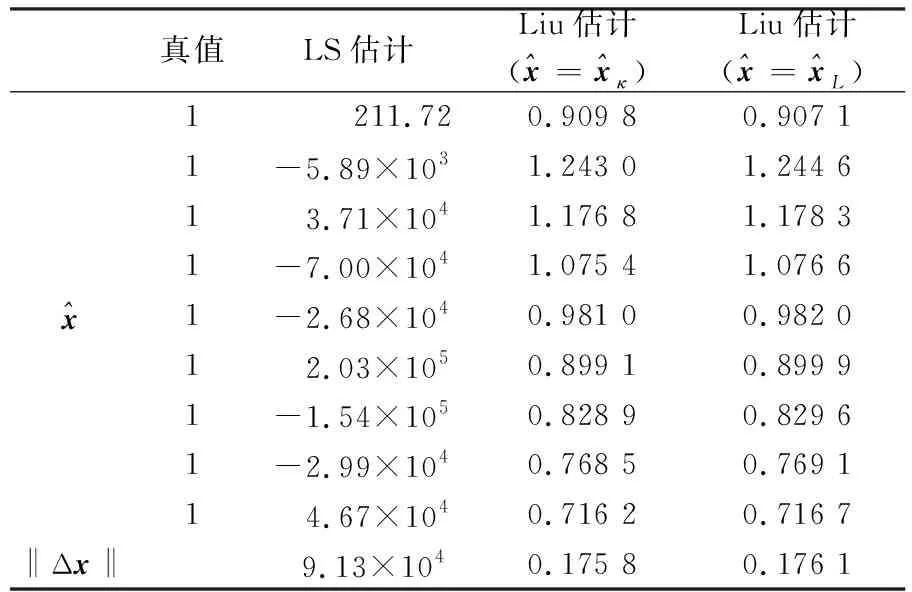
表3 σ0=0.001时不同算法解算的参数估值
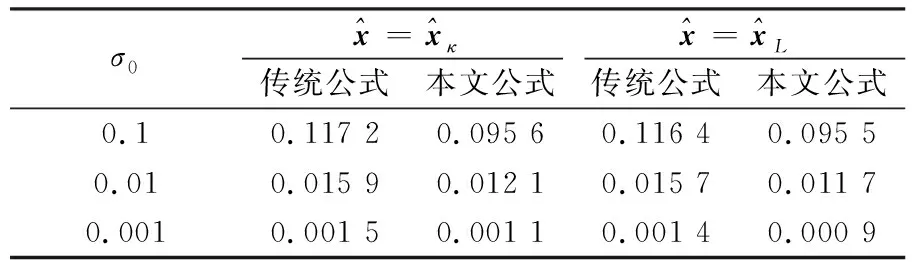
表4 本文公式和传统公式估计的单位权方差
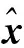
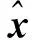
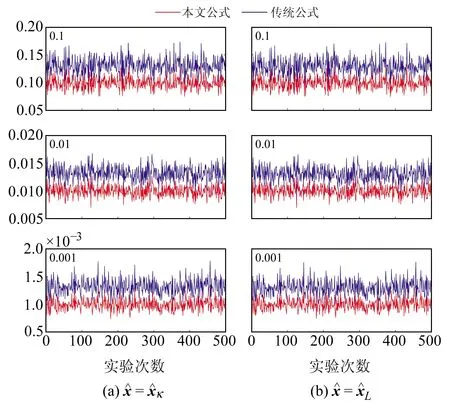
图1 500次实验2种方法估计的单位权方差Fig.1 The unit weight variance estimated by two approaches for 500 experiments
3.2 病态测边网算例
为进一步验证本文公式的有效性,模拟一个病态测边网。图2为网的点位平面分布,其中共有11个点位,包括9个已知点P1~P9和2个未知点P10、P11,P10和P11的真实坐标分别为(0,0,0)和(7,10,-5)。表5为P10、P11坐标及其到已知点的距离观测值,各观测值的精度均为5 mm。现要求利用这些距离观测值求解未知点的坐标。本算例中,由于测边网的几何构型较差,其观测方程的法矩阵条件数为4.585 1×103,存在病态。
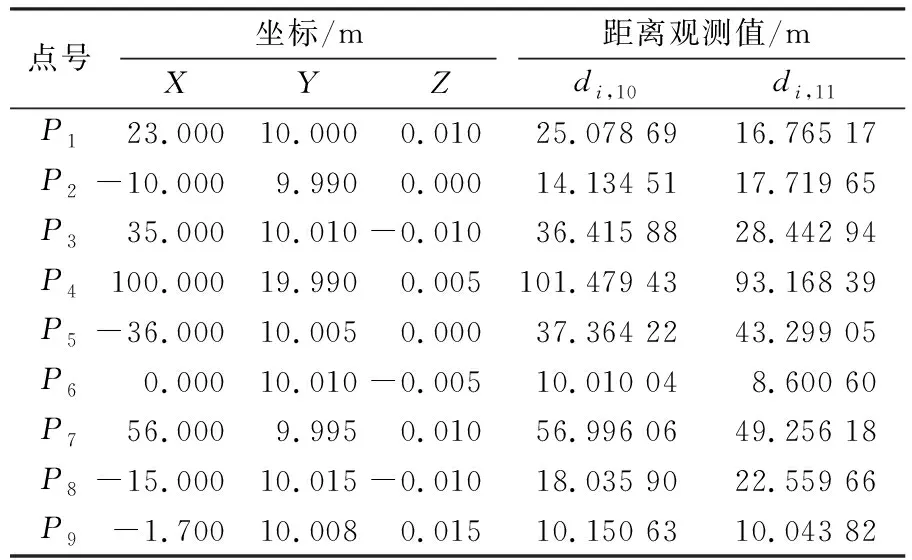
表5 控制点的坐标及距离观测值

图2 空间测边网的点位平面分布Fig.2 The distribution of the points of the space net in XY plane
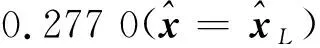
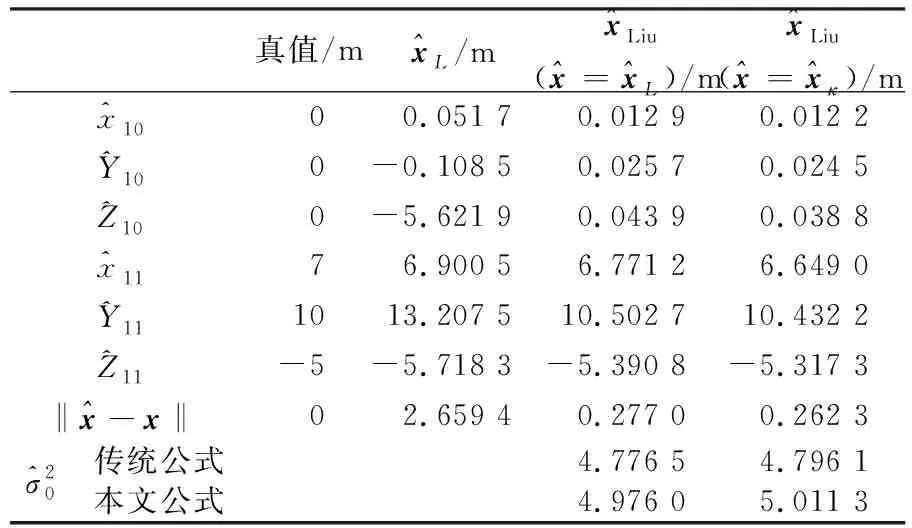
表6 不同算法解算的参数估值及与真值的差值范数
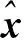
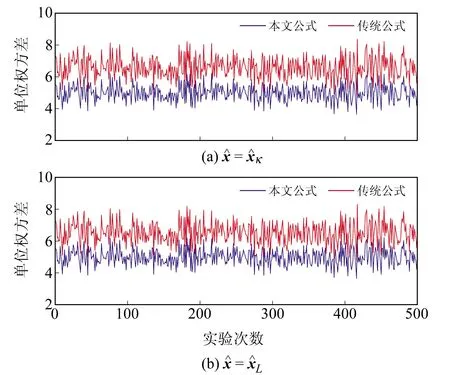
图3 500次实验2种方法估计的单位权方差Fig.3 The unit weight variance estimated by two approaches for 500 experiments
4 结 语
Liu 估计是病态模型的常用解法之一,其通过引入正则化参数和修正因子有效地削弱了系数阵小奇异值对参数估值及其方差的放大,但同时也引进了偏差,进一步导致其残差也是有偏的。本文首先计算了Liu估计残差的偏差,并将其从残差中剔除,得到偏差改正后的残差;然后基于向量二次型的数学期望公式,利用改正后的残差导出Liu估计的单位权方差估计公式;最后设计2个算例对本文公式进行验证。结果表明,残差中的偏差会严重影响单位权方差的估计,在将偏差从残差中扣除后,利用改正后的残差估计的单位权方差更符合实际情形。

