基于Focal损失SSDAE的变压器故障诊断方法

武天府，刘征，王志强，李劲松，李国锋

(大连理工大学电气工程学院,辽宁 大连 116024)

0 引言

电力变压器是电力系统运行的核心设备，准确诊断变压器内部潜伏性故障对于电网安全运行具有重要意义[1]。油中溶解气体分析(dissolved gas analysis，DGA)是诊断和检测变压器内部潜伏性故障的有效方法[2—3]，并在此基础上形成了三比值法、改良三比值法等变压器故障诊断方法[4—5]。此方法的基本原理是在变压器发生故障时，根据从变压器油中提取的特征气体含量算出相应的三对比值并赋予相应的编码，再由编码规则得到一组编码表，然后根据表中提供的诊断标准找到相应的故障类型。但上述方法在实践过程中逐渐显露出编码不全、判断标准过于绝对等缺点[6]。为了克服上述弊端，国内外学者展开了深入研究，部分学者提出了基于人工智能算法的变压器故障诊断方法，如专家系统[7]、支持向量机(support vector machine,SVM)法[8]、模糊理论法[9—10]、人工神经网络(artificial neural network，ANN)法[11]等。专家系统需要大量正确的专家经验，实际应用较困难[12]；SVM法本质上是二分类算法，变压器故障诊断为多分类问题，面对多分类问题，参数设置及构造分类器过程均较为繁琐[13]；模糊理论法需要人为设置初始聚类中心，诊断效果受初始聚类中心限制较大[10]；ANN法存在收敛速度慢，易陷入局部最优解的缺陷[11]。

上述变压器故障诊断方法均属于浅层机器学习方法，面对变压器故障诊断，存在学习能力不足、深层特征挖掘困难等缺点，进而影响变压器故障诊断效果[14]。相比于浅层学习方法，深度学习的本质是通过构造多隐藏层的神经网络，将数据进行非线性映射，可以实现对原始特征的深层挖掘及分析[15]。自编码器(auto-encoder，AE)是深度学习的重要组成部分，在无监督学习及非线性特征提取过程中扮演着重要角色[16]。通过堆叠多个AE形成栈式AE，能够提取原始数据中更深层次的信息[17]。

然而在针对分类问题的常见深度学习方法中，损失函数一般使用交叉熵损失，并未考虑样本不平衡对诊断结果的影响，而变压器运行及监测过程中较难获得完备样本。为此，文中提出一种基于Focal损失栈式稀疏降噪自编码器(stack sparse denoising auto-encoder，SSDAE)的变压器故障诊断方法。通过Focal损失来削弱因样本不平衡带来的不利影响。基于具体的算例进行了验证，结果表明文中方法具有良好的诊断性能。

1 SSDAE模型

1.1 AE

AE是一种经典的无监督网络，是实现无监督数据特征提取的一种方法。AE输出层与输入层神经元个数相等，输入层到隐藏层的部分为编码器，而隐藏层到输出层的部分为解码器[18],结构如图1所示。

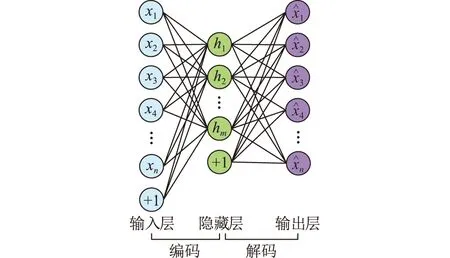
图1 AE结构Fig.1 AE structure

编码和解码的过程可分别由式(1)、式(2)表示，即：

h=f(W1x+b1)

(1)

(2)

式中：W1∈Rn×m为编码权重矩阵；b1∈Rm为编码偏置向量；W2∈Rm×n为解码权重矩阵；b2∈Rn为解码偏置向量；f(·)，g(·)分别为编码、解码过程非线性激活函数，一般采用Relu函数。

1.2 栈式稀疏自编码器(SSAE)

当AE中隐藏层节点数大于输入层节点数时，应对隐藏层施加一定约束。文中选择在损失函数中增加惩罚因子项，对AE进行稀疏性限制，进而构成稀疏自编码器(sparse auto-encoder，SAE)，SAE的代价函数为[18]：

(3)

(4)

(5)

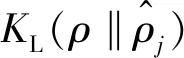
SAE仍为浅层学习模型，为了实现特征深度提取，可按照栈式结构对SAE进行堆叠，且前一层网络的输出作为后一层网络的输入，进而构建栈式稀疏自编码器(stack sparse auto-encoder，SSAE)。

1.3 SSDAE

SSDAE是在SSAE的基础上，对原始的输入数据加入噪声，将变化后的数据输入SSAE模型中，令其尽可能重构一个与原始数据相同的输出。对原始输入数据增加噪声通常有2种方式。一种是增加一个较小的随机扰动，通常为高斯白噪声，如式(6)所示。

(6)

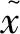
另一种是随机把输入向量中的一部分分量按概率赋值为0。文中选用第一种增加噪声方式，通过增加噪声，SSDAE迫使编码器学习提取重要的特征并学习输入数据中更加鲁棒的表征，同时增加模型的泛化能力。

SSDAE神经网络分为无监督预训练和有监督微调2个阶段。

(1)无监督预训练阶段。该阶段基于无标签样本数据，利用式(3)所示的损失函数，采用逐层贪婪训练策略，利用反向传播算法，依次实现SSDAE各层网络参数的训练。

(2)有监督微调阶段。该阶段去掉SSDAE的解码层，并加入Softmax分类层，基于交叉熵损失函数，利用反向传播算法对各层网络参数进行优化。其中交叉熵损失函数可由式(7)表示。

(7)

1.4 Focal损失函数

对于分类任务，通常采用交叉熵损失函数[19]。文中使用的变压器故障数据样本中，正常样本所占比例大且故障类样本之间存在着不平衡，使用交叉熵损失函数会使训练后的模型向样本多的类别偏移。Focal损失函数可以有效地解决上述问题，其公式为：

(8)

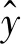
通过增加训练样本少的类别学习强度，减少训练样本多的类别学习强度，来消除类别样本不平衡对结果的影响。文中采用文献[20]的方法，具体而言，任意2个类别权重之比等于这2个类别样本数量的反比。设数据类别总数为N，则第i类的参数αi等于类别权重值，如式(9)所示。聚焦参数γ设置为2[21]。

(9)

式中：ni为第i类样本总数；αi为第i类样本的平衡参数；M为类别总数。

文中使用Focal损失函数来代替式(7)，减小样本数多的类别所对应的损失权重，增大样本数少的类别所对应的损失权重，使得模型更多地关注样本数少的类别，从而提高模型对变压器故障诊断的准确率。

2 基于Focal损失SSDAE的变压器故障诊断

2.1 输入量的确定

油浸式变压器内的油/纸绝缘材料在热和电场的作用下会逐渐老化和分解，产生少量的各种低分子烃类及二氧化碳、一氧化碳等气体。若有放电和过热故障时，油中溶解气体组分和含量会随之改变，因此，一般选取氢气(H2)、甲烷(CH4)、乙炔(C2H2)、乙烯(C2H4)、乙烷(C2H6)这5种气体作为特种气体来判断变压器的故障类型。由于这5种气体含量值差异较大，为了使SSDAE网络有良好的收敛性，将输入数据进行归一化处理，将各种溶解气体含量换算为[0,1]范围内的相对含量，如式(10)所示。

(10)

式中：x′i为归一化后的数据；xi为第i种气体的原始浓度数据；ximin，ximax分别为第i种气体浓度的最小值和最大值。

2.2 输出量的确定

参照IEC 60599规定，变压器故障类型包括局部放电、低能放电、高能放电、低温过热、中温过热及高温过热。可对变压器故障状态进行ont_hot编码，如表1所示。

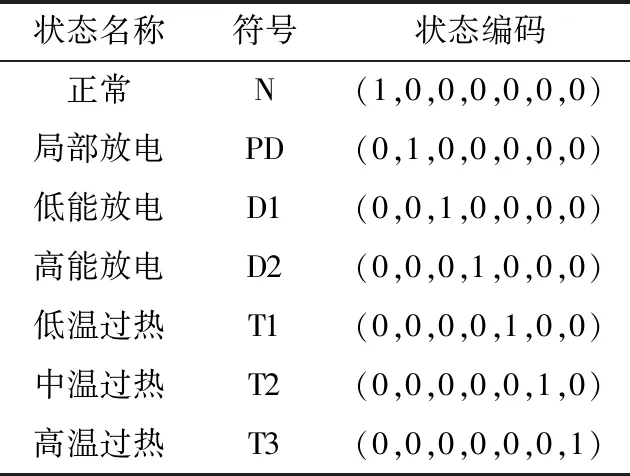
表1 变压器运行状态编码Table 1 Transformer operation status code

2.3 变压器故障诊断模型

变压器诊断模型输入为H2、CH4、C2H2、C2H4、C2H6这5种气体含量经过归一化后的值，首先加入解码层，以输出等于输入预训练网络参数；然后去除解码层，加入Softmax分类层，模型的输出为7个概率值，对应变压器的7个运行状态，取概率最大的标签所对应的故障类型为模型诊断结果。基本结构如图2所示。

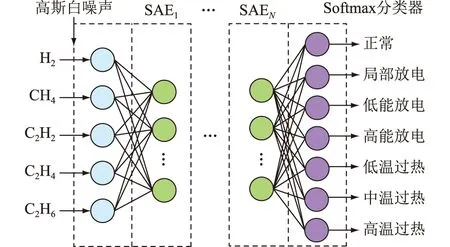
图2 变压器故障诊断模型基本结构Fig.2 The basic structure of transformer fault diagnosis model

建立SSDAE的变压器故障诊断模型需要经过1.2节所述2个训练阶段以得到最终的训练模型。为了加快训练速度，采用自适应学习率，学习率调整系数设置为0.5，最大迭代次数为1 000次。

2.4 变压器故障诊断流程

基于Focal损失SSDAE的变压器故障诊断包括数据预处理、模型参数设置、无监督预训练、有监督微调和输出分类结果5个过程，其诊断流程如图3所示。

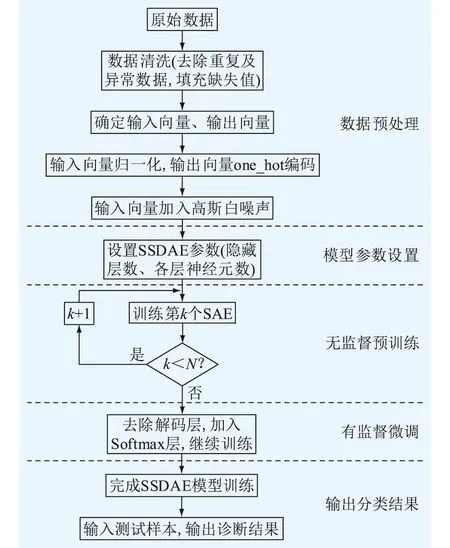
图3 变压器故障诊断流程Fig.3 Transformer fault diagnosis process

3 案例分析

为了验证基于Focal损失SSDAE的变压器故障诊断效果，选取某供电公司提供的变压器DGA故障数据，共1 518组。变压器的故障数据中存在人为或传感器等因素造成的重复或异常数据。重复数据会使模型更偏向于重复样本的类别，因此需进行数据去重。异常数据会使模型的准确率降低，因此使用Tukey′s test法对异常值进行检测，执行过程如式(11)和式(12)所示[22]。

UL=Q3+1.5IQR

(11)

DL=Q1-1.5IQR

(12)

式中：UL为上边界；DL为下边界；Q1为下四分位数，即25%分位数；Q3为上四分位数，即75%分位数；IQR为上、下四分位数差，即分位距。

异常数据的判断标准为大于上边界或小于下边界。检测到的异常数据被删除并视为缺失值。根据原始样本的7个状态，采用随机森林法对缺失值进行数据填充。

经过上述数据清洗，剩余892组非重复数据将用于后续模型的训练及结果预测。取各类样本的80%组成训练样本集，各类样本的20%组成测试样本集。各运行状态下训练样本及测试样本组成如表2所示。

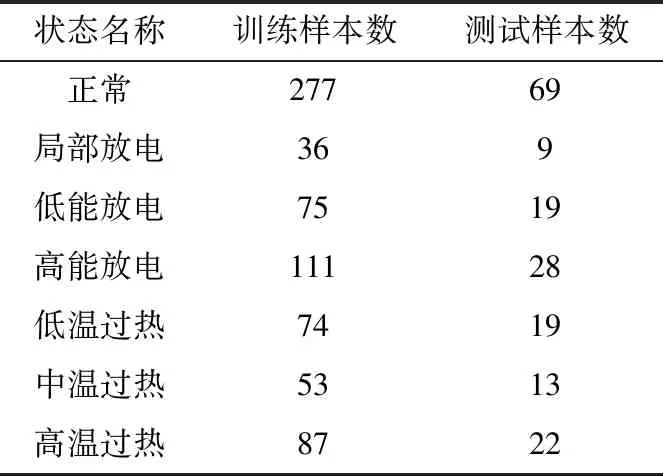
表2 故障样本统计Table 2 Fault sample statistics

为了使SSDAE模型有较好的效果，需先明确隐藏层及神经元理想数值。文献[22]指出，当隐藏层数超过3层时，很难优化权重，因此文中设置隐藏层的层数为3。隐藏层神经元的数目根据经验可由式(13)得出，对于所有的隐藏层使用相同数量的神经元个数。

(13)

式中：Nh为隐藏层神经元的数目；Ns为训练集样本数；Ni为输入神经元的数目；No为输出神经元的数目；α为任意取值变量，通常取1～5。由此可得到隐藏层的神经元个数分别为58，29，19，14，11，进而得出网络的最佳性能，如图4所示。

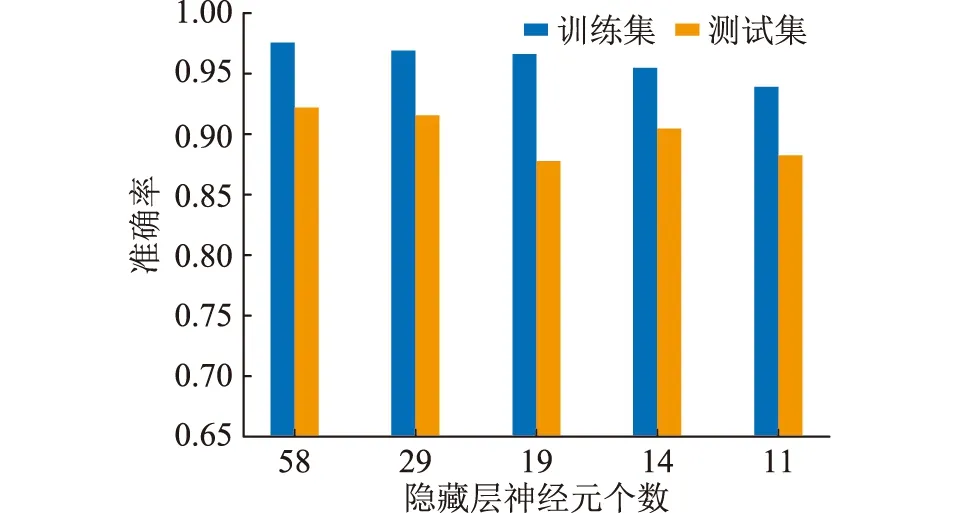
图4 隐藏层神经元数目对网络性能的影响Fig.4 Influence of the number of hidden layer neurons on network performance

由图4可知，当隐藏层设置为3层，且隐藏层神经元的个数为58时，模型的准确率最高。据此，文中所提的SSDAE网络的结构为：5(输入层)—58(第一隐藏层)—58(第二隐藏层)—58(第三隐藏层)—7(输出层)。

为了确定式(6)中系数μ的值，分别选取了0.001～0.01之间的10个值进行计算，并与未加入高斯白噪声的模型进行对比，得到结果如图5所示。在加入0.001倍的高斯白噪声后，模型的准确率得到提升。但是，随着加入高斯白噪声的增加，模型的准确率呈现下降趋势。为了使模型达到最好的效果，文中μ取0.001。

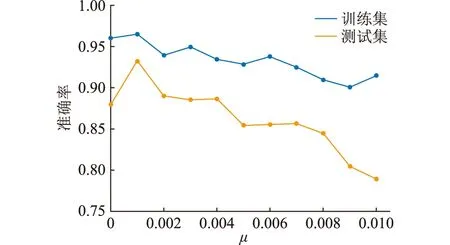
图5 高斯白噪声对模型准确率的影响Fig.5 Influence of Gaussian white noise on model accuracy

为明确SSDAE网络模型的性能，分别采用三比值法、SVM、决策树、随机森林、反向传播神经网络(back propagation neural network,BPNN)、SSAE+交叉熵损失函数和SSDAE+交叉熵损失函数对相同的数据集进行训练和故障诊断。SVM采用径向基函数(radial basis function,RBF)作为核函数，核函数参数设置为0.5，规则化稀疏设置为500；随机森林和决策树设置为默认值；BPNN输入层为5个神经元，隐藏层为58个神经元，输出层为7个神经元，输出层加Softmax分类器；SSAE+交叉熵损失和SSDAE+加交叉熵损失模型参数设置与文中方法一致。测试样本为179个，各故障诊断结果如表3所示，混淆矩阵的结果如图6所示,其中各个子图分别为各模型在变压器数据集上的混淆矩阵结果，图中色块颜色深浅仅代表数值大小。

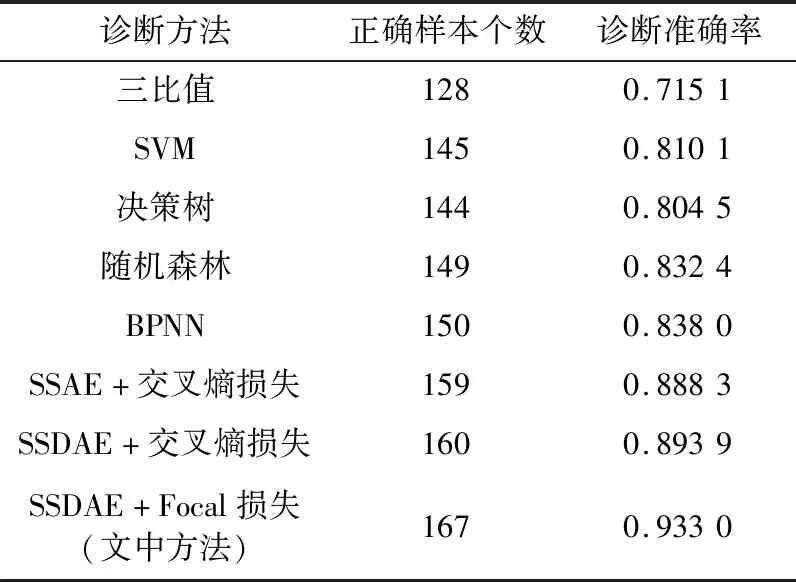
表3 不同方法诊断结果Table 3 Diagnostic results of different methods

由表3和图6结果可知：

图6 各模型在变压器数据集上的混淆矩阵Fig.6 Confusion matrix of each model on transformer data set

(1)三比值法故障编码少，部分故障用三比值法难于诊断，且三比值法的判断标准过于绝对,导致三比值法的准确率偏低。

(2)对于深层特征的提取能力，文中方法优于传统的SVM、决策树、随机森林和BPNN等浅层模型，其准确率也高于传统方法。

(3)在SSAE的输入向量中加入高斯白噪声，可以避免模型的过拟合，增加了模型的泛化能力。因此SSDAE模型的准确率高于SSAE的准确率。

(4)训练样本不平衡易造成模型产生偏向性，进而影响模型对故障的诊断效果。而在变压器的故障诊断中，样本不平衡无法避免，文中采用Focal损失函数可进一步降低样本不平衡的影响。

4 结论

文中分析了SSDAE的结构和原理，提出一种基于Focal损失SSDAE，利用变压器中的5种特征气体含量作为模型的输入量，7类运作状态作为输出量，经过训练得到了变压器故障诊断方法。有如下结论：

(1)SSDAE能有效地提取数据的深层特征，且加入高斯白噪声能提升模型的泛化能力，从而提高模型的分类准确率。

(2)在实际运行中，较难获得变压器的完备样本，主要表现为正常样本远多于故障样本且各故障类样本也存在不平衡，导致模型准确率偏低。基于Focal损失SSDAE能有效解决样本不平衡带来的准确率偏低的问题。

(3)与传统的机器学习方法，如SVM、决策树、随机森林和BPNN相比，基于Focal损失SSDAE的故障诊断方法具有更高的诊断准确率。

诊断模型的评价指标除准确性外，还有模型的稳定性。对于所提变压器故障诊断模型的稳定性文中并未涉及，有待后续研究。

本文得到中央高校基本科研业务费(DUT20RC(3)018)资助，谨此致谢！