基于偏最大信息系数与组合XGBoost的短期风功率预测
李科,黄东晨,陶子彬,熊欢,李浩文,杜业冬
(南瑞集团(国网电力科学研究院)有限公司,江苏 南京 211106)
0 引言
风能是一种可大规模商用的绿色可再生能源。由于风力发电具有强烈的间歇性和随机性,且周期规律不明显,当风电大规模并入电网时,可能对电网的安全及稳定运行产生不良影响[1]。因此,亟需发展精准的风功率预测技术。
围绕着短期风功率预测,国内外学者进行了诸多探索。自回归滑动平均模型(autoregressive moving average model,ARMA)假设当前时刻的值与前一时刻的值及随机干扰量均有关,具有一定捕捉时序信息的能力,是一种常用于风功率预测的时间序列分析模型[2]。但对于功率波动较大且无明显周期规律的风电场而言,使用ARMA模型会导致预测结果误差较大。人工神经网络(artificial neural network,ANN)[3—4]和支持向量机(support vector machine,SVM)[5]是另外2种经典的风功率预测模型。ANN能够自适应、自学习,以任意精度逼近任何非线性映射,非常适合描述风功率预测模型复杂与非线性的特点。但ANN训练时间长,调参过程较为繁琐,容易出现过拟合的情况[6]。相较而言,SVM有着较强的泛化能力,不易过拟合。然而,当训练样本大幅增加时,SVM的性能提升不明显[7—8]。
近年来,极限梯度提升(extreme gradient boosting,XGBoost)[9]算法由于在Kaggle、KDD等一系列大数据算法竞赛中表现优异,引发了大量的关注。XGBoost不仅在算法精度上较传统算法表现出色,同时也支持并行化运行,减少了模型的训练时间。此外,XGBoost还具有可移植性强、支持多数主流编程语言、集成了Spark等各类主流大数据平台等特性[10],这些特性增强了XGBoost的普适性,使得XGBoost在工程化应用方面具有更大的优势。目前XGBoost已经在光伏发电量预测[11—14]等多个领域有所应用。然而,仅使用单一预测模型存在一定的泛化问题,需要结合组合预测策略[15]。文献[16]以反向传播 (back propagation,BP)神经网络、线性外推和SVM为底层算法,构建一种动态调整权重分配的风电预测集成学习模型,获得了提高模型整体泛化能力的效果。然而,文中的方法缺少效率层面上的考虑。另外,在工程应用中,不同风电场适用的模型气象特征输入不同[17],需要有相应的算法选择合适的气象特征作为模型的输入变量。
综上所述,文中提出一种结合偏最大信息系数(partial maximal information coefficient,PMIC)特征选择算法的组合XGBoost短期风功率预测模型。首先,设计基于PMIC的特征选择算法,对风速、风向等常用气象特征进行优选;其次,以XGBoost为底层算法构建组合预测模型,实现对短期风功率的预测。算例结果表明,文中方法能有效提高短期风功率预测精度及计算效率,有助于工程化应用。
1 特征选择
1.1 风功率预测问题中常用的气象特征
据已有文献及现场情况,目前常用气象特征有:
(1)风速Vh,即风电场与地面相对高度为h米时的平均风速,在文中后续算例中,h的取值范围为{30,50,70,90,110}。
(2)风向Ddir,即风电场当地的平均风向。
(3)温度Ttemp,即风电场当地的平均温度。
(4)湿度Hhum,即风电场当地的平均湿度。
(5)气压Ppres,即风电场当地的平均气压。
在短期风功率预测问题中,风速是决定风电场输出功率的主导因素。由于地表粗糙度和大气热分层的影响,风速的分布并不完全遵循对数风廓线或指数风廓线,有时还会出现低海拔风速高于高海拔风速的情况。因此,在选择预测模型的特征输入时,可以考虑不同高度的风速,这样能够更好地表征风电场周围的大气特征[18]。
另外,根据文献[19],风速之外的因素也可能对风电场的功率出力情况造成影响。对于不同风电场,气象特征对输出功率的影响程度也不相同。例如,当风电场内风机空间布局密集程度较大时,尾流效应对风电场出力的影响尤其突出[20],此时风向对风功率有较大的影响。因此,需在建立模型前对特征进行选择。
1.2 基于PMIC的特征选择
最大信息系数(maximal information coefficient,MIC)是一种衡量变量间相关性程度的统计量[21],不仅能够刻画变量间的线性与非线性关系,还能够捕获变量间潜在的非函数关系。其主要思想为:如果2个变量之间具有一定的相关关系,对相应变量的散点图进行不同方案的网格划分,计算对应的互信息(mutual information,MI)值并且进行正则化,取这些值中的最大值,则该值为这2个变量的MIC。其中,MI值是衡量变量之间相关性程度的指标。给定变量X={xi},Y={yi},i=1,2,…,n,n为样本数目,其MI值定义为:
(1)
式中:f(x,y)为X和Y的联合概率密度;f(x),f(y)分别为X和Y的边缘概率密度。采用高斯函数对上述概率密度进行估计,至此,可进一步求得MI值。
给定一个有限二元数据集合D={(xi,yi)},i=1,2,…,n,将变量X划分为x个区间,Y划分为y个区间,则能够得到一个x×y的网格划分G。同样的x×y规格的网格划分方案有多种,对每一种方案,计算其MI值,取不同划分方案下Imi(X,Y)的最大值作为划分G的MI值。至此,定义集合D在划分G下的最大MI值为:
I*(D,x,y)=maxGI(D|G)
(2)
式中:D|G为集合D在G上的概率分布;I(D|G)为在该概率分布下的MI值;maxG为遍历所有可能的x×y网格G。
将所有划分方案下的最大MI值进行正则化,并组成特征矩阵M(D)x,y,定义为:
(3)
最大信息系数Imic定义为:
(4)
式中:B(n)为网格划分x×y的上限值。在文献[22]中,建议将ε设为0.6,即B(n)=n0.6。
然而,风电场相关气象特征之间普遍存在一定程度的耦合关系。为此,文中在MIC的基础上进一步引入偏互信息(partial mutual information,PMI),将MIC改造为PMIC,以消除耦合给特征选择带来的不利影响。
设X和Z为多输入系统中的输入变量,Y为输出变量。若X和Z之间具有耦合关系,将导致X和Y之间最大信息系数Imic(X,Y)的计算出现偏差。因此,文中应用条件期望mX(z)和mY(z)分别对X和Y中包含Z的信息剔除,分别记为U,V:
(5)
U=X-mX(Z)
(6)
V=Y-mY(Z)
(7)
式中:f(z)为Z的边缘概率密度函数。X和Y的PMIC记为:
Ipmic(X,Y)=Imic(U,V)
(8)
文中采用赤池信息量准则(akaike information criterion,AIC)[22]作为变量筛选的结束条件,即:
(9)
式中:ri为根据已选变量计算的Y回归残差;p为已选变量个数。随着变量的筛选,TAIC不断减小,当TAIC达到最小值时,最优自变量集合筛选完毕。
设输入变量集为F,输入变量为Y,最优输入变量集为S,FS为最大的PMIC值对应的候选变量。PMIC变量选择算法流程如下:
(1)将S初始化为空集。
(2)计算F中各变量与Y的最大信息系数Imic(Fi,Y)。
(3)选择使IMIC(Fi,Y)值最大的FS。
(4)计算TAIC值,并将FS移入S。
(5)若F≠φ,计算V=Y-mY(S);对于每一个Fj∈F,计算U=Fj-mFj(S)。
(6)选择使Imic(U,V)值最大的FS。
(7)更新TAIC值,若TAIC减小,则将FS移入S,返回步骤(5),否则终止筛选。
2 短期风功率组合预测模型
2.1 XGBoost算法原理
XGBoost是一种以决策树为基础的梯度提升算法,计算速度快,模型表现好。给定含有N个样本和M个气象特征的训练样本集D={(xi,yi)}(i=1,2,…,N,xi∈RM,yi∈R),RM为具有M个维度的实数集。XGBoost算法使用由K个回归决策树函数相加构成的集成模型对功率进行回归预测:
(10)
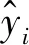
(11)

(12)
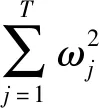

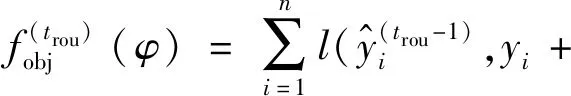
(13)
式中:ftrou(xi)为第trou轮增加的决策树函数;Ω(ftrou)为第trou轮对应的正则项,对以上目标函数进行二阶泰勒展开,并移除常数项,可得:
(14)
其中:
(15)
(16)
式中:gi,hi分别为损失函数的一、二阶导数。
通过对目标函数进行二阶泰勒展开,同时用到了一阶导数和二阶导数,有利于模型在训练集上更快地收敛。
综合式(12)和式(14),并定义:
(17)
则有:
(18)
对于一个确定的树结构qtree,其对应的最优化目标函数值为:
(19)
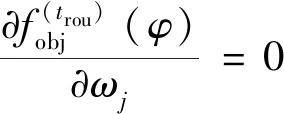
(20)
式(19)可用于衡量树结构qtree的质量。通常所有可能的树结构不可能被完全枚举出来,故XGBoost采用一种贪心算法,每次在已有的叶子节点中加入分裂。假设IL和IR为分裂后左右子节点的集合,设I=IL∪IR,则分裂后产生的信息增益如下:
(21)
式(21)通常用来评价分割的候选节点。
2.2 组合XGBoost预测模型构建
组合预测能有效综合多个单一模型的信息,减少单个模型的预测风险,提升算法整体的预测精度[23—24]。由此,文中结合前文阐述的基于PMIC的特征选择算法,构建以XGBoost为底层算法的组合预测模型。相应的训练流程如图1所示。
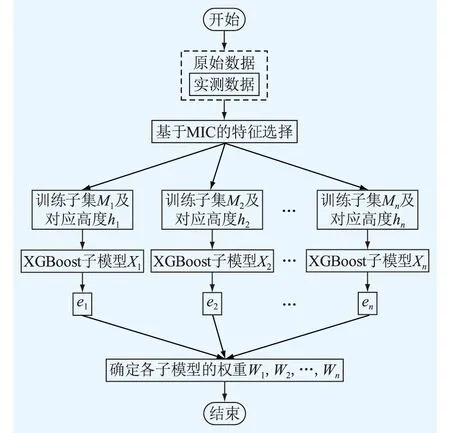
图1 组合XGBoost模型训练流程Fig.1 Training process of combined XGBoost model
(1)对原始特征集执行基于PMIC的特征选择操作。
(2)根据选择出的风速高度将相应的数据集分成n个训练子集{M1,M2,…,Mn}。
(3)利用XGBoost分别对n个训练子集进行训练,生成n个子模型X1,X2,…,Xn,利用测试集及均方误差对每个子模型的预测误差ei进行评估,计算公式为:
(22)

(4)利用熵权法对各子模型进行权重分配。
相应的预测流程如图2所示。

图2 组合XGBoost模型预测流程Fig.2 Forecasting process of combined XGBoost model
(1)对预测集进行包含特征选择在内的数据预处理工作,并根据风速高度将处理后的预测集分成n个预测子集N1,N2,…,Nn。
(2)利用训练流程生成的各XGBoost子模型X1,X2,…,Xn及对应权重W1,W2,…,Wn对测试样本进行计算,得出预测结果。
3 算例分析
3.1 数据集与模型评价指标
为充分论证文中所提方法性能,文中采用华东某风电场A、西北某风电场B的实测数据及历史数值天气预报数据进行了相关实验。其中,风电场A的平均风速较小,波动相对稳定;而风电场B则平均风速较大,波动性较强。表1和表2分别为2个风电场数据的数据概况及相关风电机组的主要参数。

表1 风电场A和B的数据概况Table 1 The data overview of wind farms A and B

表2 风电场A和B的风电机组主要参数Table 2 Main parameters of wind turbines in wind farms A and B
训练阶段的输入为测风塔不同高度的风速数据及风电场当地的平均风向、温度、湿度及气压数据,输出为实测功率。测试阶段的输入为对应的数值天气预报数据,输出为预测功率。对于短期功率预测,后一天的数值天气预报数据由预报供应商于前一天的6点前发布。
在数据预处理方面,采用文献[25]中数据预处理方法对训练集数据进行预处理。
在模型精度评价方面,参考国家电网颁布的《风功率预测功能规范》[26],选用均方根误差、平均绝对误差和合格率作为风电场功率预测的精度的评价指标,各指标的具体定义如下。
均方根误差:
(23)
平均绝对误差:
(24)
合格率:
(25)
其中:
(26)
式中:Pft为t时刻预测功率值;Pt为t时刻实测功率值;Sop为风电场的额定装机容量。
3.2 特征选择
为得到2个风电场的最优特征子集,利用PMI对MIC进行改造,构建一种基于PMIC的特征选择算法,相应的特征选择过程分别如图3、图4所示。对于风电场A而言,当第4个特征被选出来时,TAIC最小,为-86 275。对于风电场B而言,当第5个特征被选出来时,TAIC最小,为-97 553。相应的特征选择结果如表3所示。
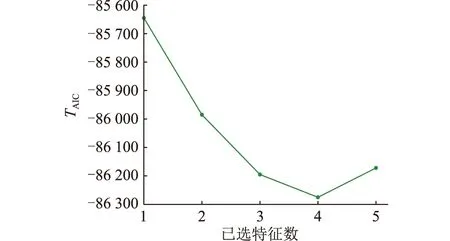
图3 风电场A对应的特征选择过程Fig.3 Feature selection process corresponding to wind farm A

图4 风电场B对应的特征选择过程Fig.4 Feature selection process corresponding to wind farm B

表3 风电场A和B对应的最优特征子集Table 3 The optimal feature subsets for wind farms A and B
表3中,如文中1.1节所述,V30,V70,V90分别表示30 m,70 m,90 m层高对应的风速特征。在不同高度的风速特征选择方面,风电场A比风电场B少选了110 m风速,这是由于风电场A风机风轮扫风范围所限。在其他气候条件选择方面,风电场B选择了风向和温度,风电场A则只选择了气压,表明不同风电场的输出功率对气候条件的敏感程度不同。
3.3 算法整体预测效果分析
为了验证组合XGBoost模型在解决短期风功率预测问题上的有效性,文中首先将未经特征选择的单一预测模型ARMA、SVM、BP、XGBoost、结合了PMIC的XGBoost(PMIC-XGBoost)与结合了PMIC的组合XGBoost(PMIC-CXGBoost)作为类比模型同时进行风功率预测,并从训练效率和模型精度两方面进行验证。
以风电场A中的训练数据为基础,图5为不同未经特征选择的单一预测模型在相同迭代次数下的训练耗时。可见,XGBoost模型训练耗时要远低于其他模型,展现了其在模型训练效率方面的优越性。其原因在于,XGBoost在效率上进行了多方面优化,包括基于列存储块的并行学习实现、采用缓存感知访问、外存块计算等。因此,选择XGBoost作为底层算法能使组合模型具备更高的计算效率。
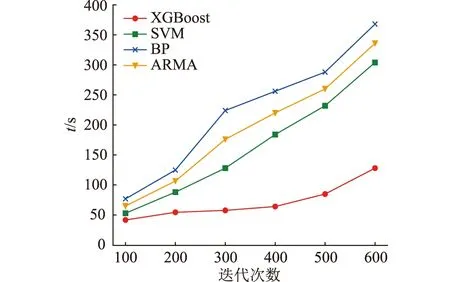
图5 模型训练耗时与迭代次数的关系Fig.5 Relationship between model training time and number of iterations
表4为不同模型对于风电场A和风电场B的预测结果。可见,风电场A具有远低于风电场B的均方根误差和平均绝对误差,同时也有更高的合格率,表明平均风速小,波动相对稳定的风电场的输出功率更好预测。当由风电场A切换到风电场B时,ARMA、SVM、BP的预测效果均急剧下降,而基于XGBoost模型,即XGBoost,PMIC-XGBoost,PMIC-CXGBoost仍能有10%左右的均方根误差及7%以下的平均绝对误差,合格率则均在87%上。统计结果表明,XGBoost在模型精度方面相较其他单一预测模型更加优越且稳定,这是因为XGBoost的设计同时考虑了学习能力与泛化能力。在学习能力方面,XGBoost是一种由若干决策树组成的集成学习模型,决策树的个数理论上可以任意大,意味着XGBoost可以更灵活地对训练样本进行拟合,从样本中学习更加丰富的信息。另外,XGBoost针对目标函数进行二阶泰勒展开,在对一阶导数进行保留的同时加入二阶导数,能够使模型在训练集上更容易收敛。在泛化能力方面,XGBoost 算法在正则项上对单颗树中叶节点的数量及叶节点的权重均进行了控制,避免模型出现过拟合,进而提升模型在训练集外的泛化能力。

表4 不同模型的预测结果Table 4 The forecasting results of different models %
比较单一XGBoost和PMIC-XGBoost:对于风电场A,PMIC-XGBoost的均方根误差和平均绝对误差相较单一XGBoost分别下降了1.39%和1.27%,合格率提升了1.65%;对于风电场B,PMIC-XGBoost的均方根误差和平均绝对误差也相较单一XGBoost分别下降了1.67%和1.16%,合格率提升了1.43%。该结果验证了基于PMIC的特征选择算法的有效性。
比较PMIC-XGBoost和PMIC-CXGBoost:无论是风电场A还是风电场B,PMIC-CXGBoost模型整体的均方根误差、平均绝对误差都要小于PMIC-XGBoost,其合格率也高于PMIC-XGBoost。其中,风电场A的均方根误差和平均绝对误差分别相较PMIC-XGBoost低了1.69%和1.84%,合格率相较高了2.44%;风电场B的均方根误差和平均绝对误差分别相较PMIC-XGBoost低了1.84%和2.1%,合格率相较高了2.61%。该结果表明,引入组合预测的思想后,预测效果有了进一步的提升。
表5比较了文中组合预测方法PMIC-CXGBoost与其他相近组合预测方法的性能,类比模型为文献[16]中的集成学习预测模型,底层算法的迭代次数设为300。文献[16]中的模型也将不同高度的风速作为模型的输入,底层算法则采用了BP神经网络、线性外推和线性SVM,对应风电场A和风电场B。与文献[16]中的集成学习预测模型相比,文中所提组合XGBoost不仅具有更优的精度,也具备更短的训练时间。

表5 文中组合预测方法PMIC-CXGBoost和文献[16]中的预测方法的对比Table 5 Comparison of the proposed combination forecasting method PMIC-CXGBoost and the forecasting method in reference 16
图6和图7分别为文中方法在2个风电场中风功率预测值和实测值的比较。可以看出,文中方法能很好地预测实测序列的变化趋势。

图6 风电场A中组合XGBoost预测值与实测值的比较Fig.6 Comparison of forecasting and measured values of combined XGBoost in wind farm A

图7 风电场B中组合XGBoost预测值与实测值的比较Fig.7 Comparison of forecasting and measured values of combined XGBoost in wind farm B
4 结语
针对当前短期风功率预测中存在的精度以及工程化应用问题,文中提出一种将PMIC特征选择与组合XGBoost相结合的预测模型。一方面,引入PMI对MIC进行改造,使相关特征选择算法不仅能得到对风功率影响程度较大的气象特征,也有利于消除变量间的耦合关系。另一方面,为兼顾算法的精度和效率,减少单个模型的预测风险,采用XGBoost作为底层算法构建组合预测模型。将2个具有较大差异的风电场作为算例进行验证,实验结果表明,结合了PMIC特征选择的组合XGBoost模型不仅在精度方面效果理想,在计算效率方面,也较相近组合预测模型有更好的效果,便于工程化应用。
在下一步工作中,将考虑将误差修正技术引入组合XGBoost预测模型中,使得算法整体上具备更好的反馈能力,以进一步提升短期风功率的预测精度。

