城市轨道交通不间断供电系统蓄电池容量改进整定算法
郭阳,李舜康,梁君,施祎辰,黄学良
(1.苏州轨道交通集团有限公司,江苏 苏州 215000)2.东南大学电气工程学院,江苏 南京 210096)
0 引言
我国的城市轨道交通弱电系统主要由通信系统、综合监控系统以及乘客信息系统等组成。不间断电源(uninterruptible power supply,UPS)对于电气设备、系统的可靠性至关重要[1],是信息和通信系统的关键组件,可通过保持系统电源的连续性和质量来确保可靠性[2]。UPS可以保障失电情况下弱电系统的可靠供电[3],因此目前国内轨道交通线路大部分采用了集中供电的UPS系统[4]。为了保证UPS装置可靠运行[5],需要根据UPS容量大小与后备时间要求配备蓄电池作为后备电源。
但在实际工程建设中,由于设计时缺乏准确的资料,估算中往往所保留的裕度过大,造成了UPS容量与蓄电池容量配置严重浪费。首先,蓄电池容量整定基于UPS额定容量,但估计UPS容量时一般仅将各系统所需要设备的预估负荷简单相加,再乘以一定的裕度系数,没有考虑不同类负荷特性上的差异,造成UPS提资和实际需求的较大差异[6]。其次,城市轨道交通系统蓄电池容量整定时是将设备看作恒功率模型[3],基于所带负载的总额定功率乘以最大供电需求时间计算蓄电池容量,没有考虑负载的运行特性及不同供电需求时间,导致蓄电池容量设计裕度过大。
针对UPS设计容量偏大问题的研究较少,文献[7]根据轨道交通实际运行情况,将实际负荷运行状况下的功率相加,并乘以一定的裕度系数,得出UPS新的容量整定结果。一方面,由于各系统需求分析和提资时就考虑了一定的安全裕度,而各设备长期工作时的容量一般低于其最大容量,导致设备本身的负荷率不会太高。另一方面,UPS下各负荷同时工作的场合较少,简单相加的结果和整体实际运行负荷相去甚远。且该方法更多依赖运行数据的统计结果和人为经验,缺乏对负荷特性的分析和足够的理论依据。
针对蓄电池定容问题,往往假定设备以UPS恒定功率运行,之后两小时作为后备时间计算电池后备容量。文献[8]指出,恒功率计算模型在计算不同后备时间负荷容量时会造成容量过大的问题。蓄电池的应用范围较广,在其他行业中同样存在定容问题,也有学者进行了相关研究。文献[9]针对发电厂蓄电池容量整定问题,采取容量换算法计算容量。该方法不但得出的结果偏大较多,而且需要电压水平校验。针对变电站内直流负荷的蓄电池容量计算问题,较多文献采用阶梯负荷法得到了变电站蓄电池容量计算的改进方法[10],但在进行直流负荷统计的过程中未对最大负荷做出预测。
为节约城市轨道交通不间断供电系统的蓄电池投资,加强对UPS及蓄电池容量整定二者关系的研究,提出一种新的容量削减方法。首先分析了传统UPS容量整定方法,指出其容量整定过大的原因。然后根据负荷的不同特性进行负荷聚类,对于波动性较大的负荷,利用负荷持续曲线(load duration curve,LDC)来模拟UPS所带负荷的特性,采用Weibull分布拟合该曲线以预测最大运行负荷;对于平稳负荷,采用负荷系数法预测最大运行负荷,将各类负荷预测结果之和作为蓄电池容量计算的基础。接着,根据不同负荷后备时间不同导致不同时刻放电电流大小不一致的性质,采用阶梯负荷法削减蓄电池容量。最后以苏州轨道交通3号线为例,削减了某车站通信系统的UPS蓄电池容量。
1 负荷聚类
负荷聚类分析是开展负荷特性分析、负荷建模等工作的基础[11]。对于轨道交通不间断供电系统所带负荷,有的负荷具有较大的波动性,其随着人流量等因素呈现周期性变化规律;有的负荷则较为平稳,与时序关联性不明显。因此,有必要根据设备的特点,通过对历史负荷曲线进行聚类,为后续最大负荷预测打下基础。
文中采用近邻传播(affinity propagation,AP)算法对UPS所带负荷进行特征分析,具体原理可参考文献[12]。相比其他聚类算法,AP算法具有精度高、速度快的优势[13]。此算法采取待聚类元素相似度矩阵,即取二者之间的负欧氏距离[14]:
(1)
式中:S(i,j)为场景i与场景j间的相似度;Ri,t,Rj,t分别为场景i,j在t时刻的状态。参考度p=S(k,k)表示第k个场景成为聚类中心的可能,p的初值关系到最终的聚类个数,将其设为矩阵的均值。
(2)
矩阵S(i,k)表征了场景k作为场景i聚类中心的概率。对于其他场景k′,S(i,k′)表示场景k′作为场景i聚类中心的几率,而a(i,k′)表示i对k′的认可度,两者之和就是k′成为i聚类中心的合理度。那么可定义场景k对场景i的吸引度为:
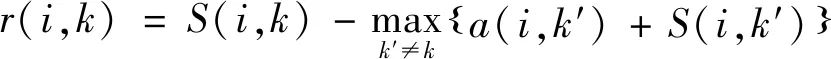
(3)
a(i,k)描述了场景i将场景k作聚类中心的倾向性,含义是:如果场景k是场景i以外的其他场景i′的聚类中心的倾向性很高,那么k成为i的聚类中心的倾向性也很高。

(4)
为了避免AP聚类算法迭代过程中的振荡,在每次迭代中加上[0.5,1]的阻尼系数λ。
rnew(i,k)=λrold(i,k)+(1-λ)r(i,k)
(5)
anew(i,k)=λaold(i,k)+(1-λ)a(i,k)
(6)
式中:rold,rnew分别为更新前、后的吸引度;aold,anew分别为更新前、后作为聚类中心的倾向性。
迭代完成后,首先判定聚类中心,当式(7)为正时,可将该场景作为中心。然后为每个j选择相应的聚类中心,即选择与场景j的吸引度和认可度之和最大的场景i作为场景j的聚类中心。
r(i,i)+a(i,i)>0
(7)
为评价聚类的效果,文中采用戴维森堡丁指数(Davies-Bouldin index,DBI)指标来评价[15]。具体聚类个数下的聚类效果,其值越小,聚类效果越好:
(8)
式中:K为聚类个数;Ri为第i类的最大合适度。可根据组内紧致度Gi和组间离散度Mij计算:
(9)
Mij=||Ai-Aj||2
(10)
式中:Ni为类i的场景数;Xj为类i的第j个场景;Ai,Aj分别为类i,j的中心;Mij为类i聚类中心与类j聚类中心的距离,反映了2类之间的离散程度。可以看出,Gi越小,第i类中场景与聚类中心越紧密。综合两者可计算合适度并给出第i类的最大合适度:
(11)
2 UPS实际最大负荷预测
对UPS下负载数据进行统计发现,不同负荷的波动性存在着较大差异。对于比较平稳的负荷,最大运行负荷只需在其历史最大负荷基础上考虑一定的备用。对于波动性较大的负荷,要提炼波动性特征并建立合适的预测模型,以真实反映波动特性。故文中分别采用2种预测,提出适应不同种类的最大负荷预测模型,以提供给蓄电池容量削减较为准确的UPS容量数据。
2.1 波动负荷最大负荷预测
地铁负荷和周边环境和人流量等存在一定的关联性,其特性不可能在短期内发生较大改变[16],可以根据其最近期的历史数据,形成等效LDC。LDC可以反映峰值和峰谷负荷之间的差异性,对其进行模拟可以反映该负荷的波动特性,因此可以通过该曲线进行最大负荷预测。
LDC是将设备功率按照从大至小的顺序重新排序后得到的曲线。在应用过程中常将其横、纵坐标互换,得到转置LDC。将转置LDC分别进行标幺处理后的曲线称为等效LDC[16],如图1所示。
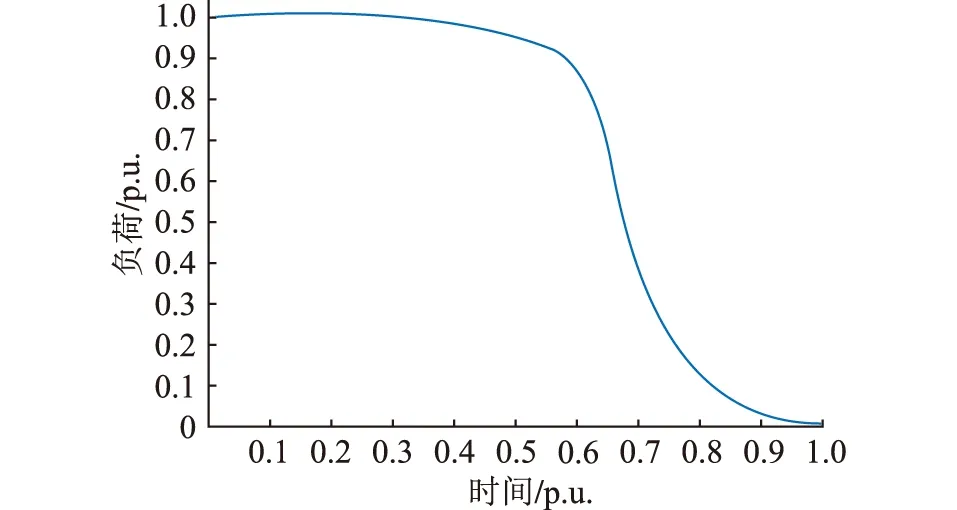
图1 典型等效LDCFig.1 Typical equivalent LDC
该曲线上的点为设备运行功率值大于该点的概率,如式(12)所示。
FLDC(x)=p(L*>x)
(12)
式中:FLDC(x)为负荷持续曲线;p(L*>x)为标幺值L*大于x的概率。由式(12)可知,可以用某种概率分布函数表述负荷特性。
经试验分析可知,大多数的LDC可采取双参数Weibull分布拟合表征。该分布曲线的双参数可以较好地表征功率曲线的形状与峰谷负荷信息。
由于等效LDC的定义与随机变量分布函数定义的累积方向不同,且曲线中最小负荷左边的部分恒等于小时数,需要对双参数Weibull分布做适当变换。得到实际LDC与等效LDC(Weibull分布函数曲线)的关系如式(13)所示。
(13)
式中:t为用电小时数;Pmin,Pmax分别为负荷最小值和最大值。
基于Weibull分布的LDC拟合模型为:
Fldc(x)=e-(x/c)k
(14)
拟合时,以上模型中的参数c与k可由非线性最小二乘法确定。
现分析拟合模型中参数与系统负荷的关系,以双参数Weibull分布为例,若假设负荷服从Weibull分布,则总用电量为:
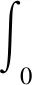
(15)
其中,
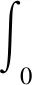
(16)
令:
s=(x/c)k
(17)
得:
(18)
其中Γ为gamma函数:
(19)
由式(18)可见,Weibull函数的参数c,k与平均负荷有紧密联系。参数c与总电量呈线性关系,而参数k则表征系统峰谷差的大小,间接影响系统总电量,均具有较为明显的物理意义。
拟合得到LDC并不能直接用于UPS最大运行负荷的确定,因为该曲线是基于历史数据的,还需要考虑UPS所带设备未来功率增长变动等情况。因此,文中提出采用基于双参数Weibull的功率曲线预测模型:
(20)
式中:λ为与预测相关的功率增长因子;β为与峰谷功率差相关的峰谷因子。β反映了预测负荷在最大值与最小值至今波动变化的情况,预测时可取0.8~1.2。β取值小于1.0时,表示高负荷时段所占比重增加;反之,表示比重降低,可以结合实际UPS负荷情况确定。
由以上分析可知,使用该模型对波动负荷进行预测,调整相关参数,即可有效预测未来的LDC和最大负荷。
2.2 平稳负荷最大负荷预测
对于用电较为平稳的设备而言,其负荷随时间变化的周期特性并不明显,采用传统的负荷系数法进行最大负荷预测似乎更为合理。文中将设备类型分为2类:连续运行负荷A和备用运行负荷B。其主要计算过程如下:
Pmax=xA+yB
(21)
式中:Pmax为最大运行负荷;负荷系数x一般为100%(当负荷为办公室电源时,x取90%),y为30%。
当得到不同类型最大运行负荷预测后,可根据后备时间和所在系统将其重新整合,得出UPS所带负荷的最终预测结果。
文中针对不同设备类型,采用不同的预测方法进行最大功率预测。选用的2种方法操作简单,参数少,预测精准且具有一定的物理意义。方法不仅可以表征历史数据,还可以设定模型参数,预测未来设备最大功率。如果用于新城市轨道交通不间断供电系统设计,可以采用相似地铁线路的数据拟合得到该曲线,并根据专家经验等设定不同的负荷因子即可。
3 基于阶梯符合法的蓄电池容量削减
根据分析,城市轨道交通通信系统蓄电池容量偏大的原因主要来源于UPS和蓄电池2个方面。文中将从蓄电池定容方面提出新的蓄电池容量削减方法。考虑到已经安装的UPS很难减容,用UPS最大预测负荷来进行计算,为后续站点容量整定提供借鉴。同时,考虑不同类负荷及其后备供电时间的关系,将蓄电池容量计算中的恒功率模型替换成阶梯负荷模式,进一步进行削减。
根据安装地点的不同,UPS所带负荷也不完全一致,不同负荷的后备时间要求也有所不同。基于第2章的预测方法,首先需要分析不同类负荷和其后备供电时间要求的关系。在此基础上,文中采用目前轨道交通蓄电池定容较少使用的阶梯负荷法进一步削减蓄电池容量[17],其步骤是按照各个阶段的放电电流分别整定各阶段的蓄电池容量,比较后取最大值[18—20]。该方法以终止电压不低于最低允许电压为前提,利用事故放电电流和容量系数求得经常负荷和事故负荷所对应容量,因此不需要校验放电电压水平,如图2所示。
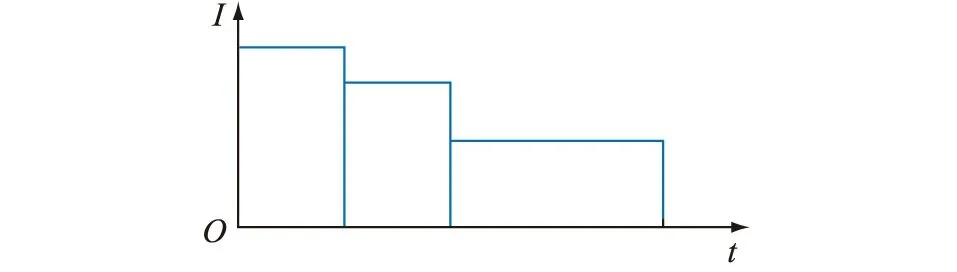
图2 阶梯负荷示意Fig.2 Schematic diagram of stepped load
根据放电电流水平的不同将放电过程分为不同的阶段,分别对不同阶段的蓄电池所需容量进行整定:
(1)计算第一阶段蓄电池放电所需容量。
Cc1=KkI1/Kc1
(22)
(2)计算第二阶段蓄电池放电所需容量。
(23)
(3)计算第三阶段蓄电池放电所需容量。
(24)
式中:Kk为裕度系数;Kc1为放电过程全阶段容量换算系数;Kc2为放电过程除去第一阶段容量换算系数;Kc3为放电过程除去第一、第二阶段容量换算系数;I1,I2,I3分别为第一、二、三阶段放电电流大小。
剩余放电过程以此类推,求出所有阶段所需的蓄电池整定容量后,取所需最大整定容量作为此次全过程放电最终容量整定结果。
综上,文中按照如下方法进行不间断供电系统蓄电池容量削减:
(1)根据UPS所带负荷进行负荷聚类,再根据负荷聚类结果将负荷分为波动负荷和平稳负荷。
(2)针对波动负荷,采用双参数Weibull模拟负荷曲线预测最大负荷;针对平稳负荷,采用负荷系数法进行负荷预测,并将二者预测结果相加,得出UPS所带最大负荷预测结果。
(3)根据最大负荷预测结果,采用阶梯负荷法,计算该预测结果下蓄电池所需容量。
4 轨道交通通信不间断供电系统蓄电池容量削减算例
苏州地铁3号线,是苏州市第四条建成运营的线路。该线路于2015年1月20日开始建设,2019年8月18日开始试运行,2019年12月25日开通。以苏州地铁轨道交通3号线某站通信系统为例,验证文中所提出的蓄电池容量削减方法。该车站UPS所承载负荷有:通信子系统包含的各项设备负荷,综合监控系统包含的各项设备负荷,乘客信息系统负荷以及自助检票系统负荷。
4.1 西津桥站原UPS及蓄电池容量计算方法
4.1.1 原UPS容量整定方法
在苏州地铁设计阶段,根据表1的各方提资,该车站通信系统总负荷为52.975 4 kW,保留一定安全裕度,根据功耗向上取整。苏州地铁3号线该车站负荷按54 kW配置,功率因数取0.8,采用80 kV·A的UPS作为电源主机。

表1 苏州地铁车站负荷提资统计Table 1 Statistics of load raising of Suzhou metro station
4.1.2 原蓄电池容量整定方法
基于上述整定方法确定的UPS容量后,假定设备以UPS恒定功率运行,蓄电池按每组39节配置,计算可得负荷电流I=134.999 A。以后两小时作为后备时间,根据国家标准[21],t和电池温度系数一般取15 ℃和0.006。取T=2,K=1.25,根据厂家提供数据放电系数η=0.61,带入容量计算公式:
Q≥KIT/(0.94η)
(25)
则相应所需蓄电池容量为588.59 A·h。
4.2 负荷聚类结果
对UPS所带负荷进行分析,根据不同类型负荷进行聚类分析,以车站为例,得到其中负荷聚类中心结果如图3。将车站UPS所带负荷分为3类时,此时评价指标DBI值为0.335 2,最低。将文中所用算法与传统K-means算法的聚类效果比较,此时传统K-means算法DBI值为0.54,表明聚类后各场景与AP算法得到的聚类中心间的紧致程度更高,且聚类中心间的离散程度更大,体现了AP聚类算法的优点。
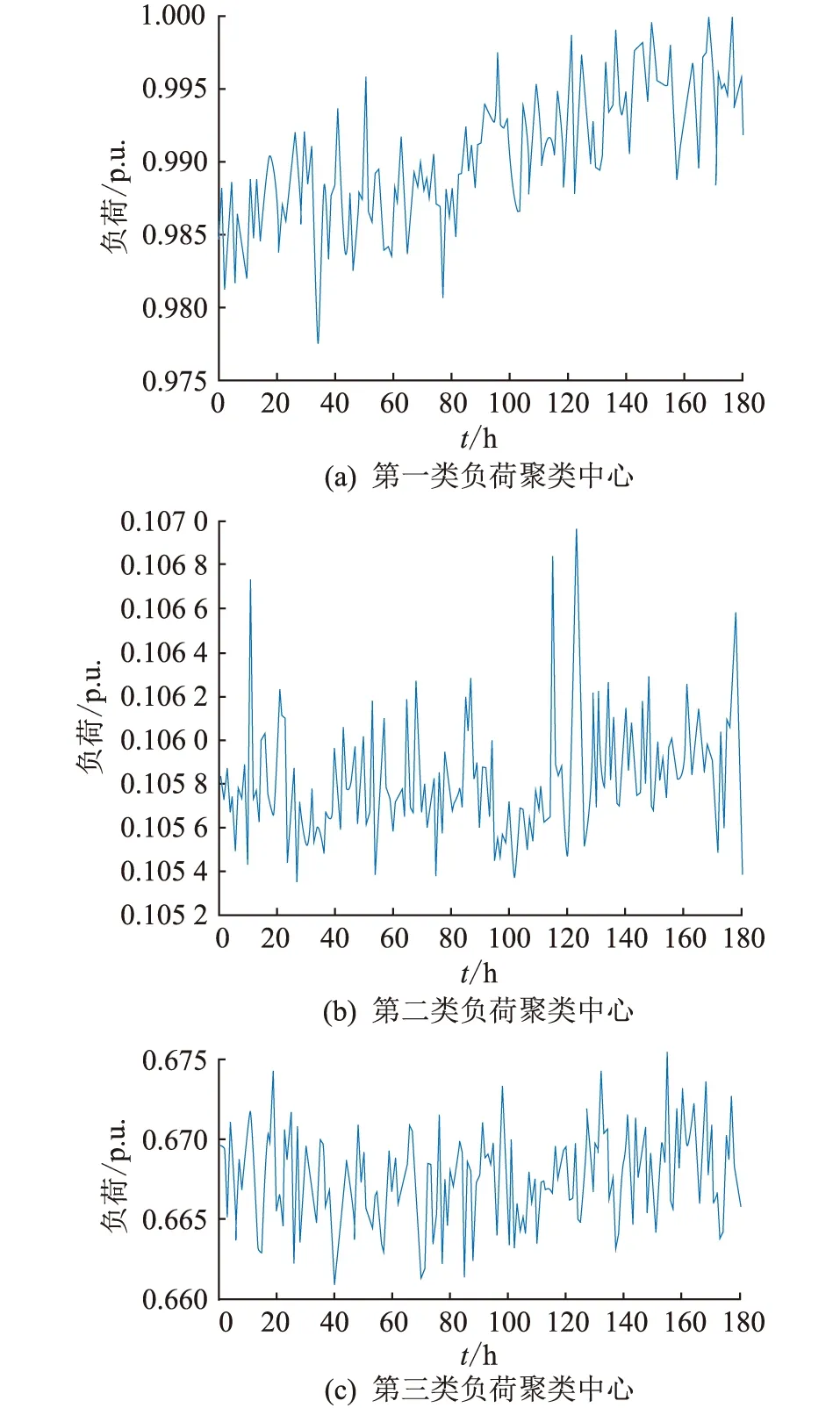
图3 车站UPS 3类负荷聚类中心Fig.3 Three kinds of load clustering center
综合监控系统和乘客信息系统为第一类负荷;自助检票系统前端设备、视频监控机柜2,3为第二类负荷;广播机柜、时钟、车控室插排等为第三类负荷。其中,第一类负荷由于检修和上下班出行高峰等原因,呈现出较强的时序相关性和波动性特征,在周末的时候整体功率呈现上升趋势。第二类和第三类负荷的时序特性并不明显,由于功率大小存在较大差异,因此分为2类,但二者的联系较为紧密且负荷特性接近,因此均可以采用稳定负荷的最大功率预测法进行预测。
4.3 车站UPS最大负荷预测
根据4.2节负荷聚类结果进行车站最大负荷预测,其中,波动负荷预测方法适用于综合监控系统和乘客信息系统,平稳负荷预测方法适用于其余2类负荷。
4.3.1 利用Weibull方法的最大负荷预测
对采集到的乘客信息系统数据进行标幺化处理,使其满足概率分布最大值为1的条件后,绘制LDC,如图4所示。
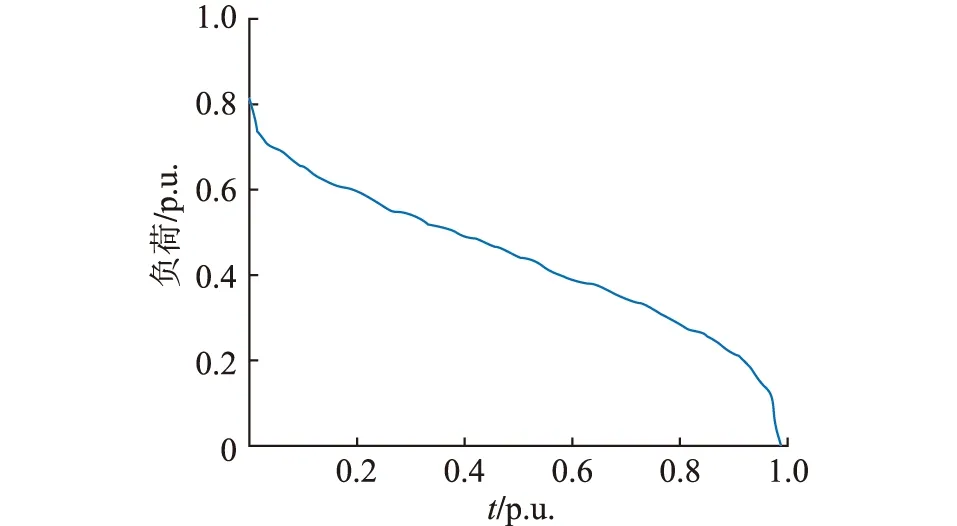
图4 车站乘客信息系统LDCFig.4 The LDC of the station passenger information system
可以看出,该LDC大致符合Weibull分布,采取第2章的负荷拟合方法,得出基于Weibull概率分布,结果如图5所示。
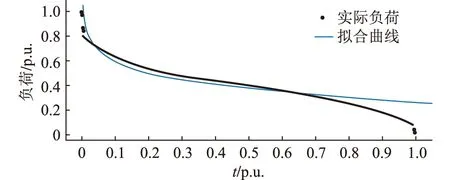
图5 车站乘客信息系统LDC拟合结果Fig.5 The LDC fitting results of the station passenger information system
由图5可以发现,当横坐标标幺值小于0.75时,拟合结果较好。当横坐标标幺值大于0.75时,由于Weibull分布右侧是不闭合的,而负荷曲线右侧是闭合的,因此出现了误差。对于此误差,没有必要纠正,这是因为:
(1)确定容量的过程中,往往更关注左侧负荷峰值情况,右侧常因检修或者其他原因导致负荷较低,参考意义不大。
(2)以下会将拟合曲线设定负荷预测参数后积分。此时Weibull分布的拟合概率大于实际概率,在积分后的总用电量大于将实际用电负荷简单相加,该部分即可作为部分安全裕度。
根据式(20),选取合适的系数,可以得出LDC预测模型。其中,根据专家经验,负荷增长因子λ取1.8,估计参数β一般在0.8~1.2之间,为防止高负荷时段有所增加并留有一定裕度,本次预测取值为0.8。
可得最大功率预测结果为:
(26)
式中:Esum为预测总用电量;P为预测功率;t为测量的总小时数。由此得出明年车站视频监控系统的负荷预测结果为3.13 kW,该值相比原来整定的负荷功率缩减了较大程度的裕度 。如果要保留更大的安全裕度,可以在此基础上再乘以整定后的裕度系数。
4.3.2 利用负荷系数法的最大负荷预测
除视频监控系统和综合监控系统外,其余2类负荷虽不属同一类,但其负荷均较为平稳,波动不大,与时间周期性关系并不明显,采用负荷系数法进行最大负荷预测较为合理。
对负荷特性进行分析,根据式(21)计算峰值负荷,裕度系数Kk根据专家建议取1.4,则得出其峰值负荷为8.45 kW。
4.4 车站蓄电池容量削减
据4.2节对苏州地铁3号线某车站通信系统负荷聚类结果显示,第一类负荷中包含乘客信息系统和综合监控系统;第二类负荷包含自主检票系统;第三类负荷包含通信子系统中各类负荷。表2则列出了该车站通信负荷的后备供电时间。
由表2可见,负荷聚类结果与工程中对各项负荷后备供电时间要求一致,说明了负荷聚类的合理性和必要性。由于两者的一致性,可以根据表2中不同后备时间内的事故放电电流,采用阶梯负荷法削减蓄电池容量。
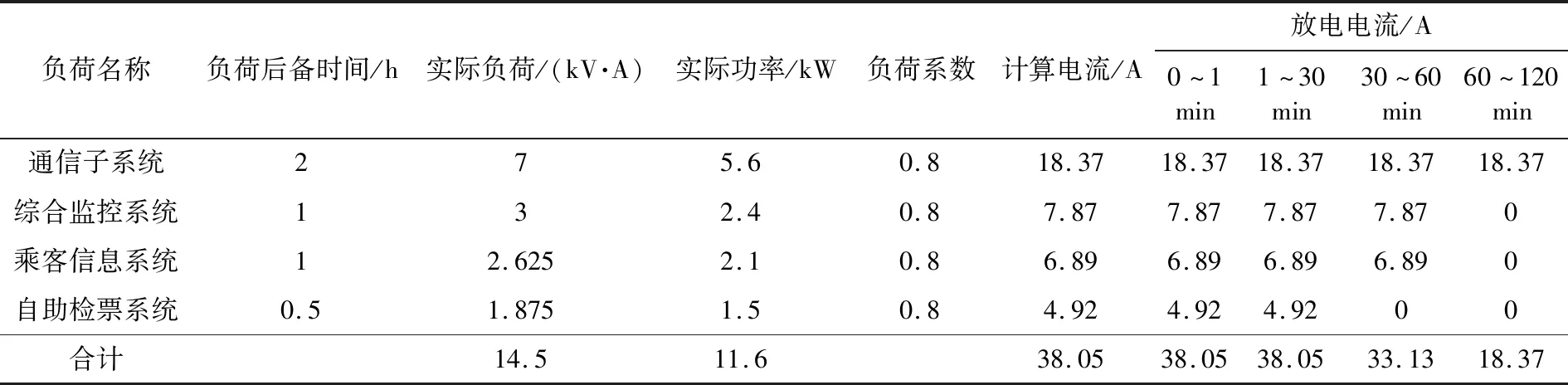
表2 地铁站负荷统计表Table 2 Load statistics of subway stations
绘制阶梯负荷电流曲线如图6所示。
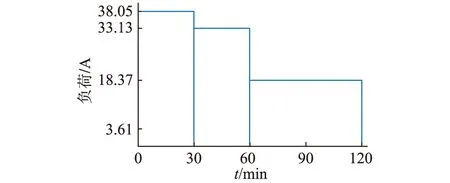
图6 地铁站负荷曲线Fig.6 Load curve of subway station
为保证直流设备的端电压大于最低电压要求,对于逆变电源装置电压波动以±10%考虑[22]。因此,集中UPS系统蓄电池放电终止电压按1.8 V考虑,电池选取阀控式密封铅酸电池。
本次容量整定时,Kk根据专家建议取1.4。根据定义,将放电分为4个阶段,放电初始阶段(0~1 min),第一阶段(1~30 min),第二阶段(30~60 min)和第三阶段(60~120 min)。其中,放电初始阶段无冲击性负荷,因此无需考虑冲击电流的影响。根据选定的终止电压和蓄电池型号以及放电时间,查询相关数据,得到不同时刻的容量选择系数表[7]。
按照不同的放电阶段,根据容量选择系数表计算不同时刻的蓄电池所需容量,并选取所需容量最大的阶段作为最终整定的结果,具体计算结果如下:
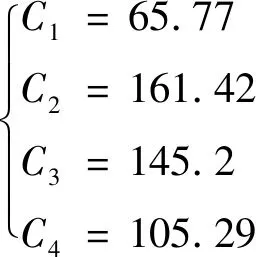
(27)
经计算,第二阶段计算容量最大,为161.42 A·h,选取容量为200 A·h。与原先计算方法整定的588.39 A·h以及不采用阶梯负荷法的整定值176.95 A·h相比,缩减了蓄电池所需的容量储备,避免了投资浪费。
5 结语
文中提出一种新的城市轨道交通不间断供电系统的蓄电池容量削减技术。针对UPS容量偏大的问题,对负荷进行聚类后针对不同类型负荷采用不同预测方法。考虑到传统恒功率模型没有计及负载的运行特性和供电需求,采用阶梯负荷法计算蓄电池容量。最后,将所提出方法应用于苏州轨道交通3号线通信不间断供电系统蓄电池的容量削减。与传统整定方法相比,文中采用的方法加强了UPS容量估算与蓄电池容量整定的关系,削减了UPS容量及蓄电池容量整定值,有效减少投资浪费。

