利用经验-过程混合建模方法优化华山松过程模型的参数*
薛海连 田相林 曹田健
(1.西北农林科技大学理学院 杨凌 712100; 2.赫尔辛基大学林学系 赫尔辛基 FI-00014;3.西北农林科技大学生态仿真优化实验室 杨凌 712100)
森林生长模型是森林生态系统动态模拟与森林经营规划的重要工具,依据模型构建方式,可分为经验模型、过程模型和混合模型(Kimmins, 2004)。传统的经验模型建模依赖大量样地调查数据,采用统计回归技术预估模型参数,准确可靠地预测林分生长和收获,但外推至建模数据之外的环境条件时应用受到限制。相比之下,过程模型的参数通过生理学观测获得,模型形式基于理论性植物与环境的关系,可外推计算环境变化对树木生长的影响(Weiskitteletal., 2011),但其结构复杂、参数繁多且参数值难以实测确定。混合模型采用半经验半机理的建模方式,一方面在机理建模的基础上结合部分经验模块,另一方面对部分机理模块进行简化,如基于生理学过程的3-PG(physiological principles in predicting growth)模型(Landsbergetal., 1997)和CABALA(CArbon BALAnce)模型(Battagliaetal., 2004)均是通过集成经验的异速生长模块来简化树木生长的机制模拟。虽然混合模型可简化模型结构且能够降低建模数据需求,但仍包含动辄数十或上百个参数。无论是过程模型还是混合模型,高维变量条件下的参数预估方法设计与选取一直是模型建模研究的焦点问题。
过程模型参数预估通常涉及树木生理、结构、功能性状等信息,这些信息往往具有一定的不确定性,有些参数甚至无法测量,只能间接推断。目前,过程模型参数预估方法主要包括同时拟合法(Sievänenetal., 1993; Vanclayetal., 1997)、Monte Carlo法(Hornbergeretal., 1985)、贝叶斯法(van Oijenetal., 2005; Siviaetal., 2006)和试错法(Mäkelä, 1997; 张廷龙等, 2011)等,其中,同时拟合法、Monte Carlo法和贝叶斯法均需先给定参数的参考值或可能的变化区间等先验信息,而后搜索计算似然值(Mäkeläetal., 2000; Mäkelä, 1988; van Oijenetal., 2005; Ewen, 2013)。如Minunno等(2019)研究CROBAS(a growth model based on crown and base dynamics)模型参数的不确定性时,基于芬兰国家森林资源连续清查数据,采用贝叶斯法校正欧洲赤松(Pinussylvestris)、挪威云杉(Piceaabies)和垂枝桦(Betulapendula)的CROBAS模型; 然而,为收敛至参数的完整联合后验分布,贝叶斯法在处理不可解析的高维模型时消耗大量时间,并需进行收敛性的反复测试(van Oijenetal., 2005; Hartigetal., 2012)。试错法主要基于实测数据、拟合数据、文献数据和专家经验等信息系统测试模型中的参数,是多数过程模型进行参数本地化的主要方法,如3-PG(Gonzalez-Beneckeetal., 2014; Xieetal., 2017)、BIOME-BGC(何丽鸿等, 2016; 曾慧卿等, 2008)和Tree-BGC(Koroletal., 1995)模型等。Mäkelä(1997)基于碳平衡原理开发的欧洲赤松CROBAS原模型,部分参数也采用试错法确定,并与林分生长经验模型预测结果进行对照。试错法相对简单易行,但变量过多时难以同时降低多个变量预测值与实测值的离差,且预测值累积误差会随着预测周期增加而逐渐增大。
模型预测准确性决定模型的应用价值,3-PG和CROBAS等过程模型之所以应用较广,也正是因其预测准确性较高(Weiskitteletal., 2011)。森林生物统计模型的可靠性还常通过不同模型的结果对比来评价。相对于Monte Carlo法和贝叶斯法,参数优化方法的优点是在处理复杂模型参数化时的收敛速度更快。不同于经典的非线性规划,种群算法(population-based algorithms)无需设定决策变量的经验初始值,对目标函数无可导可微的要求,特别是种群算法中的差分演化(differential evolution, DE)算法(Stornetal., 1997),结构简单、控制参数少、具有较强的全局收敛性和鲁棒性,更适合于解决复杂环境中的优化问题(盛万兴等, 2017)。目前,差分演化算法已被应用于包括森林经营规划(Pukkala, 2009; Arias-Rodiletal., 2015)在内的诸多领域(Lpez Cruzetal., 2003; Onwuboluetal., 2006),但其是否适用于过程模型建模仍有待证明。
本研究针对过程模型普遍存在的结构变量复杂、生理学数据获取困难的问题,以华山松过程模型CROBAS-PA(PA=Pinusarmandii)的参数优化为例,提出一种结合经验模型与过程模型的混合建模方法,探索在建模数据不足情况下预估复杂过程模型参数的有效途径。
1 研究区概况
华山松林分生长数据源于秦岭南坡中段的火地塘林区。该林区地处陕西省宁陕县境内(108°21′—108°39′E,33°18′—33°28′N), 海拔1 420~2 474 m,年均气温6~13 ℃,年降水量700~1 200 mm,属北亚热带和暖温带过渡地带。土壤主要为火成岩、变质岩、石灰岩母质上发育的弱酸性山地棕壤,厚度50~70 cm。火地塘林区华山松林面积占林地面积的22%(李悦黎等, 1993),主要分布在海拔1 600~2 200 m之间。
2 研究方法
2.1 数据来源
经验模型建模数据来源于457块角规绕测临时样地(角规系数为1)(表1),包括火地塘教学试验林场1990(244块)、2005(143块)和2013(70块)森林二类调查样地。2014年采集该林区31块20 m × 20 m固定样地的每木检尺数据(表1),按地位级(Ⅰ级13块,Ⅱ级14块,Ⅲ级4块)(吴恒等, 2015)分类,用于参数优化后的过程模型检验。

表1 华山松样地概况Tab.1 Stand attributes of P. armandii plots
2.2 经验模型及其参数预估
本研究建立的华山松经验模型QUASSI 1.0系统由式(1)~(6)构成。因缺乏优势木树高数据,故选取基准年龄时的林分平均高,即地位级指数SCI(site class index)作为立地质量评价指标。华山松林木材积与树高连年生长量在林龄30年前已明显下降(陈存根等, 1994),本研究以30年为基准年龄。式(1)为立地级导向曲线,采用Hossfeld方程,已知林分初始年龄和树高后,可由该式推算SCI并折算不同地位级指数下的树高生长过程(McDilletal., 1992);式(2)为林分密度指数(Stand density index, SDI)模型(Reineke, 1933),基于林分中立木度最高的部分样地通过参数拟合得到;式(3)和(4)是林分胸高断面积(G, m2·hm-2)模型和平均胸径(D,cm)模型,属于Schumacher模型形式(Schumacher, 1939);林分蓄积量(V, m3·hm-2)模型(式6)为华山松材积方程(陈存根等, 1996):
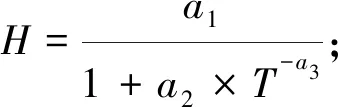
(1)
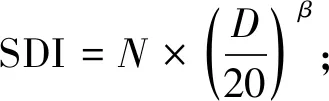
(2)
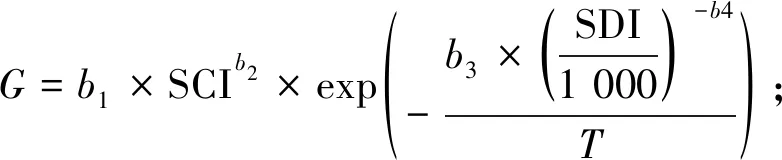
(3)
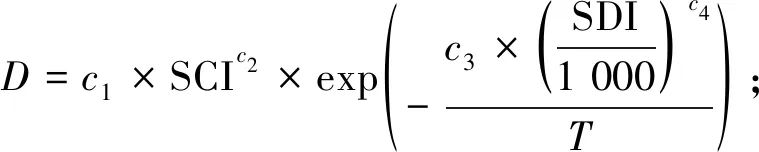
(4)
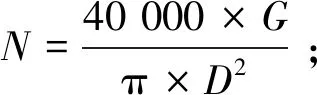
(5)
(6)
式中:H为树高(m);T为林龄(a);a1、a2、a3、b1、b2、b3、b4、c1、c2、c3、c4和β均为系数;N为林分密度(trees·hm-2)。
本模型构建数据来自表1描述的样地,参数估计值与检验见表2。
为保证检验样本独立性,按调查年份将数据分为3组(表1),采用交叉验证方法测试模型表现,最终以合并数据所获得的模型参数(表2)模拟林分生长。本研究筛选样地均为人工起源的华山松相对纯林,林分内部个体年龄差异基本在一个龄级范围内,按同龄林进行建模。式(1)为树高导向曲线,未考虑除年龄以外引起树高数据变异的因素,导致较低的决定系数。而胸径预测模型(式4)决定系数较低,是因为仅考虑了年龄、立地和林分密度3个因素,多数样地无法获取抚育、间伐、择伐的历史信息,导致数据中较高比例变异未被解释。

表2 华山松经验模型QUASSI 1.0参数估计值Tab.2 Parameter estimates of the empirical model QUASSI 1.0 for P. armandii
2.3 过程模型
华山松过程模型CROBAS-PA的原模型为Mäkelä(1997)开发的CROBAS,该模型在模拟单木各器官碳分配过程时提出3个假设(式7—9): 1) 树冠表面积(Ac, m2)与叶生物量(Wf, kg)异速相关; 2) 叶和细根生物量(Wr, kg)之比为常数; 3) 叶生物量和冠基处边材面积之比为常数(αq, m2·kg-1)(Shinozakietal., 1964)。
(7)
Wr=αrWf;
(8)
Aq=αqWf,(q=s,b,t)。
(9)
式中:Aq为各部分的边材面积;s、b、t分别代表树干、树枝、运输根;ξ′和z为参数;αr为细根与叶生物量比值。
模型链接了光合作用、呼吸作用、自然整枝、枯损等模块。华山松过程模型CROBAS-PA以初始叶生物量Wf、初始第一活枝高度Hs、林分初始密度N0为输入变量,计算模型的状态变量(亦称模型输出变量),包括林木各器官在20年间的边材面积和生物量、冠长、第一活枝高度等。
本研究通过改变细根与叶生物量比值αr和细根衰老速率sr(表3,Sr=srWf,Sr为单树细根每年的衰老量,单位为kg·a-1)反映立地条件变化,从而影响林木各器官的碳分配(Mäkeläetal., 2016; Mäkelä, 1997; Persson, 1980),即以第Ⅱ地位级参数为基准(αr=0.2,sr=1),计算CROBAS-PA第Ⅰ地位级(αr=0.1,sr=0.5)和第Ⅲ地位级(αr=0.25,sr=1.5)的参数。该方法的依据是细根与叶生物比值αr随立地质量提高而变小(Vanninenetal., 1999),即立地较差的林分会有更高比例的碳分配至细根,以提高养分水分吸收量。
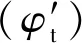
2.4 参数优化
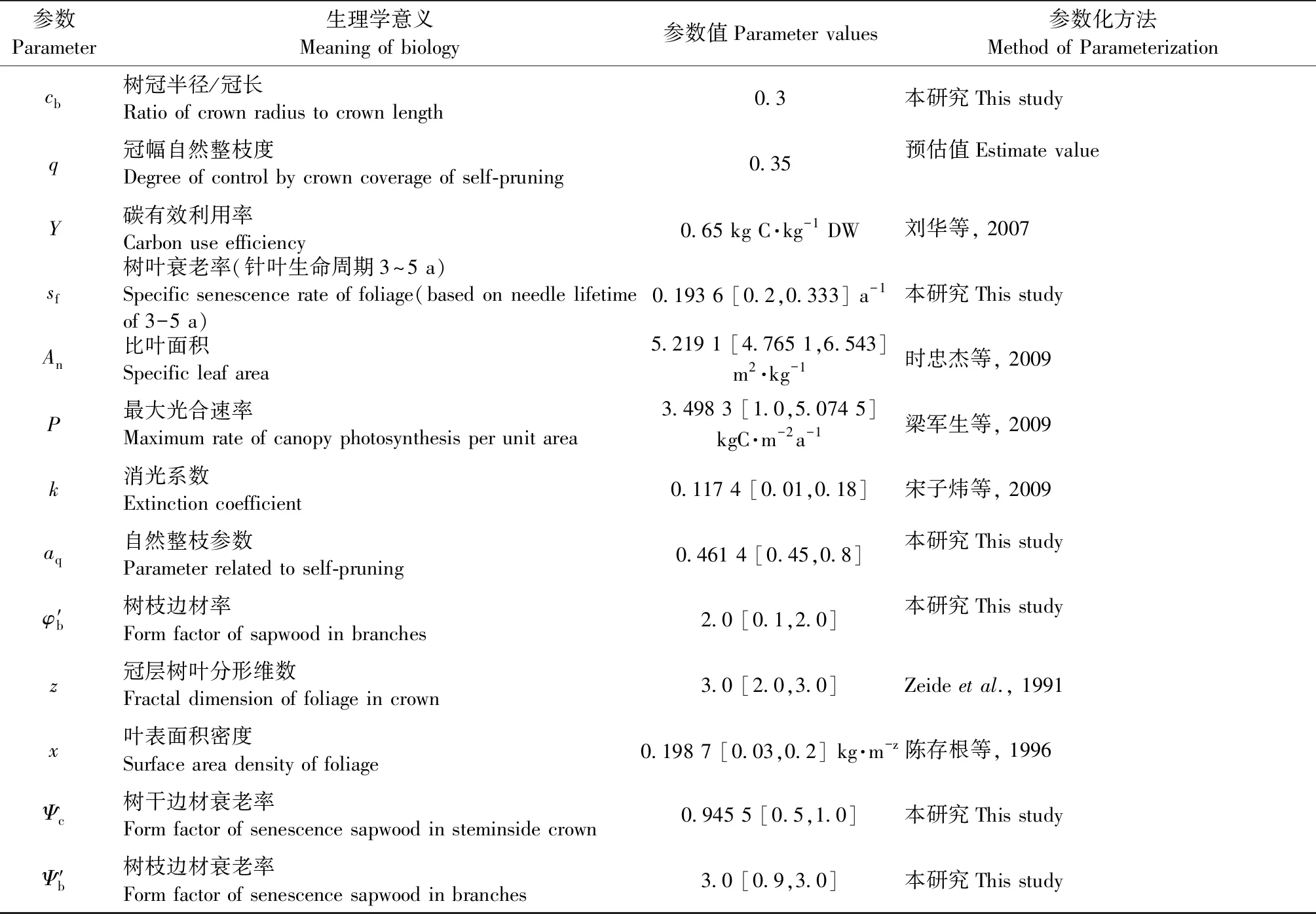
参数优化模型(式10—11)的目标函数设为过程模型CROBAS-PA与经验模型QUASSI 1.0在树高和生物量预测上的离差。
续表3 Continued
min{x1,x2,…,x10|Z0}f=∑dRRMSEd;
(10)
s.t.X=(x1,x2,…,x10),xj∈[Lj,Uj],
j=1,2,…,10 。
(11)
式中:Z0指林分初始状态;X=(x1,x2,…,x10)为决策变量x1、x2、…、x10所组成的向量,向量X中的10个元素是表3中的最后10个参数;Lj与Uj分别指xj的下界与上界;d为树高或树木各部分生物量;RRMSEd指各变量的相对均方根误差(relative root mean square error, RRMSE)。
分别利用经验模型QUASSI 1.0与过程模型CROBAS-PA模拟特定初始年龄、立地、密度条件下90块华山松样地生长过程,通过优化过程模型参数,最小化二者间的差异。样地具体信息为: 初始年龄20、30、40年,每个龄组中分别令地位级指数SCI=8、9、10、11、12、13 m,林分密度指数SDI=500、600、700、800、900。将初始年龄、SCI和SDI输入全林模型后,计算90块样地的林分初始状态及后续20年间的生长过程。20年间的叶、枝和根生物量变化可由CROBAS-PA计算,并与经验生物量公式(陈存根等, 1996)对比。
参数优化模型的决策变量选取过程模型CROBAS中基于生理学和物候学设定的10个参数,即树叶衰老率、树冠树叶分形维数、比叶面积、最大光合速率、消光系数、叶表面积密度、自然整枝参数、树枝边材率、树干边材衰老率和树枝边材衰老率。约束条件为这10个决策变量的可行域(表3)。
采用Storn等(1997)提出的差分演化算法(DE),该算法是基于“贪婪竞争”机制进行全局寻优的随机算法,通过父代变异、杂交的方式产生子代,而后由竞争机制选择最优解。DE的变异操作充分利用其他个体信息,增加了种群多样性,同时减少了单纯个体变异带来的随机性和盲目性。利用最优个体加随机个体差分法的变异方法,既提高了搜索速度,也降低了陷入局部最优的危险;但是若种群分布密度过高,也可能使其陷入局部最优。差分演化算法的初始群体从10个决策变量的可行域中随机抽取,10个决策变量的值和表3中的前26个参数一起输入CROBAS-PA模型进行优化计算,从中选取使目标函数最小的一组参数值。通过以下6个步骤执行优化搜索。
1) 初始化。产生初始种群,种群个体Xi=(xi1,xi2,…,xijD),其中xij∈[Lj,Uj],i=1,2,…,Np,j=1,2,…,D,D为自变量的维数。种群大小Np=45,缩放因子F=0.6,杂交概率CR=0.8。迭代次数Gm=50。
2) 评价初始群体。计算初始群体中各个体的适应值f(Xi),并记录最优值与最优个体。
3) 差分变异操作。在种群中随机选取不同的个体Xa、Xc、Xd、Xe、Xf,进行变异操作取得新的种群个体Vi:
rand/1Vi=Xi+F(Xa-Xc);
rand/2Vi=Xa+F1(Xc-Xd)+F2(Xe-Xf);
best/1Vi=Xb+F(Xa-Xc);
best/2Vi=Xb+F1(Xa-Xc)+F2(Xd-Xe);
current to best/1Vi=Xi+α(Xc-Xi)+F(Xa-Xc)。
式中:α为D维向量,其元素是[0,1]之间的随机数;F1、F2均为缩放因子(Liuetal., 2010)。
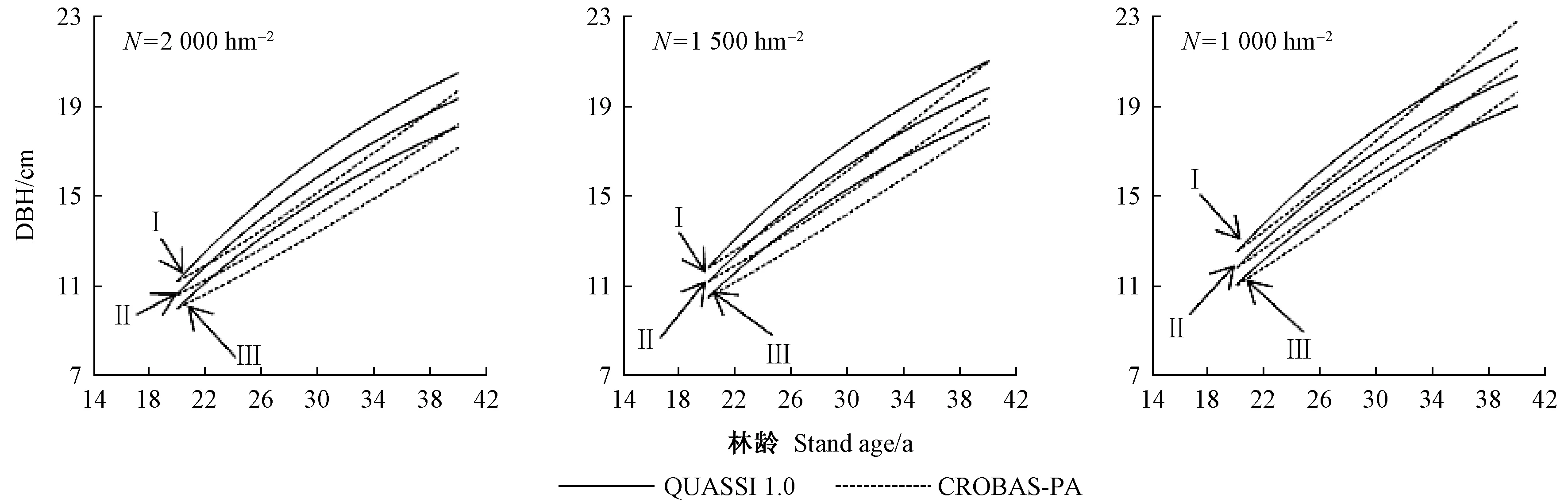
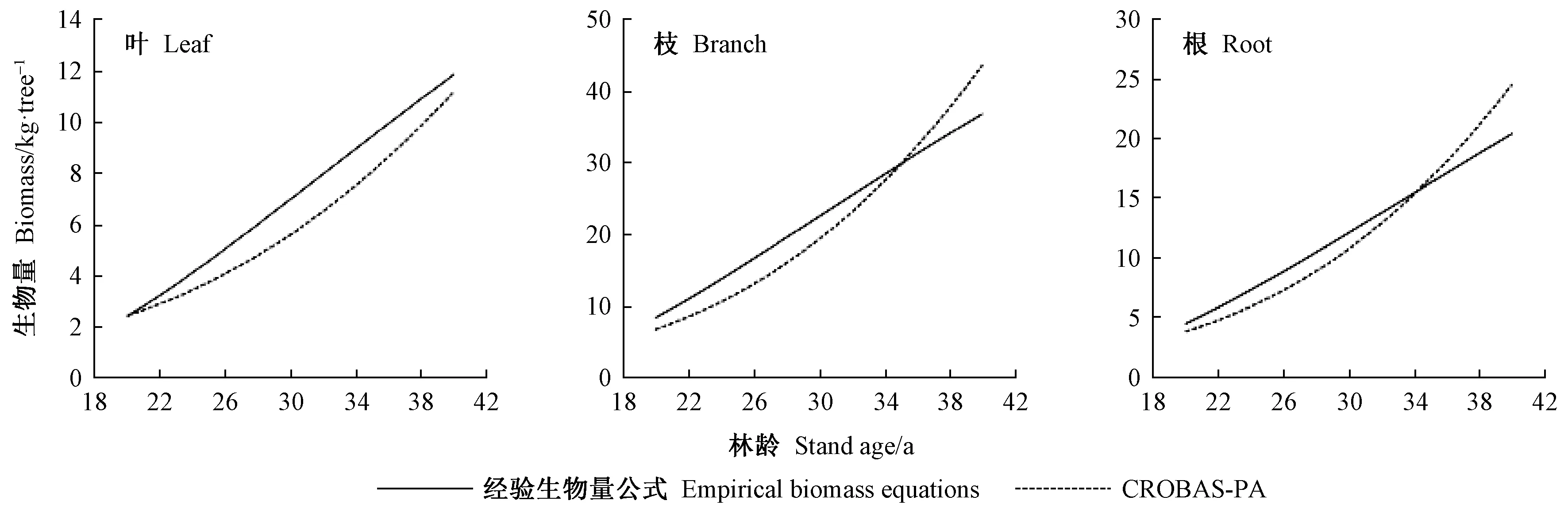
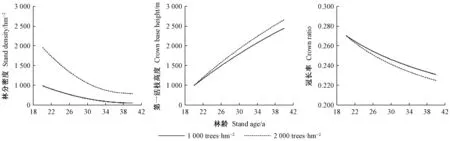
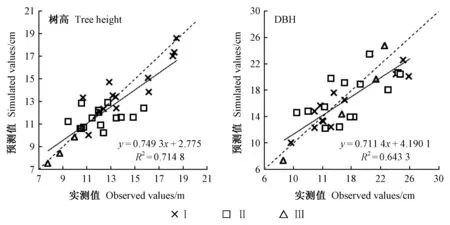
4) 杂交操作(二项式杂交)。若αj[0,1] 5) 选择操作。若f(Ui) 6) 检验是否符合条件。如果当前的迭代次数达到预定设置的最大迭代次数Gm,则停止迭代,输出最优解,否则转到步骤3。 本研究在优化算法选用时,比较了差分演化算法(DE)的6种变异方式(图1)。其中rand/2变异方式收敛速度最慢,best/1收敛速度最快,但变异方式rand/2与best/1之间的最优值竟相差5.8%。通过设置不同的初始种群,并测试其收敛结果,最后根据算法的稳定性和收敛速度选用current to best/1变异方式。 图1 算法DE的迭代过程Fig.1 Process of iteration of algorithms DE 为检验CROBAS-PA模型的准确性,以31块固定样地(表1)作为一组独立数据对参数优化后的过程模型进行验证。此外,设计不同立地(18种)、不同初始密度(5种)的90块样地(n=18×5=90),分别采用CROBAS-PA和QUASSI 1.0预测树高和胸径生长过程,而后对二者在20年间的树高和胸径预测差异进行统计学验证。使用经验模型QUASSI 1.0生成的90块虚拟样地可以避免过程模型参数优化因抽样非均衡带来的误差。具体虚拟样地包括5个林分密度指数(SDI=500、600、700、800、900)及3个地位级共18个地位级指数(第Ⅰ地位级SCI=12.3、12.7、13.1、13.5、13.9、14.3 m; 第Ⅱ地位级SCI=9.9、10.3、10.7、11.1、11.5、11.9 m; 第Ⅲ地位级SCI=7.7、8.1、8.5、8.9、9.3、9.7 m)。所用的统计量有平均误差(mean error, ME)、平均绝对误差(mean absolute error, MAE)和平均相对误差(mean relative error, MRE),3个统计量的绝对值越小,说明CROBAS-PA预测的树高和胸径越接近QUASSI 1.0 预测的树高和胸径,预测精度也越高。 本研究基于生理学意义选取12个参数(树冠树叶分形维数、消光系数、比叶面积、最大光合速率、树叶衰老率、叶表面积密度、自然整枝参数、树枝边材率、树干边材衰老率、树枝边材衰老率、细根与叶生物量比值和细根衰老速率)进行全局敏感度分析,该方法考虑了单个参数及多个参数间的相互作用对模型输出变量的影响。 应用Sobol法(Cukieretal., 1975)将过程模型全局灵敏度的目标函数设为CROBAS-PA与QUASSI 1.0在预测树高或胸径变化上的Nash-Sutcliffe效率(NSE)(Nashetal., 1970)。NSE常用于复杂模型灵敏度分析的目标函数(Yang, 2011; Nossentetal., 2011)。NSE的理论范围为-∞到1,通常0 本研究用于灵敏度分析计算的样地共36块(n=3×4×3=36,由QUASSI 1.0模拟),初始年龄分别设为20、30、40年,地位级指数SCI=6.5、8.5、10.5和12.5 m, 林分密度指数SDI=500、800、1 100。NSE具体计算公式如下(式12): (12) 过程模型CROBAS-PA与经验模型QUASSI 1.0的20~40年树高生长预测对比(图2)显示,CROBAS-PA预测的树高相较QUASSI 1.0低估0.1~1.0 m,且这种差异在地位级高的林分中更明显。在初始密度为2 000和1 500株·hm-2的样地中,CROBAS-PA预测的胸径比QUASSI 1.0低估0~1.1 cm,而在初始密度1 000株·hm-2中,CROBAS-PA预测的胸径比QUASSI 1.0高估0.6~1.2 cm(图3)。 图3 基于两种模型的不同立地与林分初始密度条件下林分胸径预测值Fig.3 Comparisons between two models for DBH developments under different site and initial density conditions 图4 经验生物量公式(陈存根等, 1996)与过程模型CROBAS-PA预测的叶生物量、枝生物量和根生物量Fig.4 Comparison between empirical biomass equations(Chen et al.,1996) and CROBAS-PA for foliage biomass, branch biomass, and root biomass predictions 图5 第Ⅱ地位级不同初始密度下的林分密度、第一活枝高度和冠长率的比较Fig.5 Comparisons of stand density, crown base height and crown ratio between stands of different initial densities in site classⅡ 本研究以中等立地与密度条件的林分为例(图4,第Ⅱ地位级、初始密度1 500株·hm-2),比较CROBAS-PA和经验生物量公式(陈存根等, 1996)预测的各器官生物量,结果表明,林龄在20~40年间,CROBAS-PA模型的叶生物量预测值偏低,枝生物量和根生物量的预测结果分别在林龄35年之前和34年之前偏低,但之后偏高。 经验模型通过林分密度控制来描述竞争,过程模型可通过第一活枝高和冠长率的变化反映林木竞争(图5)。林分枯损模块是基于林分密度指数进行构建的(Reineke, 1933)即密度高于给定SDI值的林分会自然枯损。CROBAS-PA基于林冠结构和光截留计算林冠内的荫蔽环境和自然整枝过程。密度较大的林分对空间和光照的竞争更激烈,第一活枝高度较高且冠长率较小(图5)。 固定样地实测值与过程模型CROBAS-PA预测值的相关分析表明,CROBAS-PA模型的树高和胸径预测值与实测值基本呈线性相关(图6)。即便31个用于对比的固定样地林分状况差别较大,如林龄从20到52年,林分密度从289株· hm-2到4 616株· hm-2,但树高和胸径的实测值和模型预测值的R2仍分别达到了0.714 8和0.643 3。 虚拟样地20年间的生长统计检验结果显示,CROBAS-PA模型在树高和胸径预测上存在低估,但误差较小(表4)。CROBAS-PA模型树高预测值的平均误差与平均绝对误差均低于1.03 m,平均相对误差小于5.59%,其中第Ⅰ地位级的预测误差略高,第Ⅲ地位级的预测误差则较低(表4)。CROBAS-PA胸径预测值的平均误差、平均绝对误差和平均相对误差分别小于0.36 cm、1.19 cm和2.59%,其中平均相对误差最高(2.59%),出现在第Ⅰ地位级; 最高平均误差(0.36 cm)发生于第Ⅱ地位级; 而平均绝对误差最高(1.19 cm)的为第Ⅲ地位级(表4)。 全局灵敏度Sobol分析表明(表5),最大光合速率P、树冠树叶分形维数z、消光系数k和比叶面积An对树高生长影响的总灵敏度系数排序最高,分别为0.444 3、0.361 0、0.312 9和0.301 0。胸径的总灵敏度系数排序最前的4个参数与树高一致。树高和胸径对各参数的一阶灵敏度系数之和分别为0.646 6、0.588 5,均小于1,说明该模型是不可加的,即非线性的。 图6 树高、胸径的实测值和预测值比较Fig.6 Comparison between observed and simulated values for tree height and DBH 表4 CROBAS-PA树高、胸径预测值的检验结果Tab.4 Model validation of CROBAS-PA on tree height and DBH predictions 表5 树高和胸径的一阶灵敏度系数和总灵敏度系数Tab.5 Sobol’s first-order indices and total-effect indices for height and DBH 参数优化后的过程模型CROBAS-PA可以实现华山松林木各器官生物量的预估,并预测不同立地与密度条件下林分胸径和树高的生长。灵敏度分析显示胸径和树高生长对比叶面积An、最大光合速率P、消光系数k和树冠树叶分形维数z较为敏感。 CROBAS-PA模型的树高、胸径预测误差与模型结构简化直接相关。Shcherbinina(2012)基于CROBAS预测短叶松(Pinusbanksiana)生长时,亦出现类似本研究中树高被低估的结果,其原因是细根与叶生物量比值αr的变化对树高生长的影响为间接过程(Mäkelä, 1997; Shcherbinina, 2012)。另外,本研究显示CROBAS-PA模型预测的树高生长受林分初始状态影响较小,但林分初始密度对CROBAS-PA模型预测的胸径精度有一定影响,林分密度越大时胸径预测偏差越大。由于本研究采用异速生长方程(陈存根等, 1996)约束华山松过程模型CROBAS-PA的生物量分配,简化了林分密度对叶生物量的影响,而根据叶生物量计算胸径生长,误差由此而生(图3)。 本研究的灵敏度分析证明比叶面积An、最大光合速率P、消光系数k对树高和胸径生长影响较高(表5),与Ewen(2013)的研究结果一致。Weiskittel 等(2011)指出过程模型对光合作用、光截留方面的参数是非常敏感的。增加An、P、k意味着光合作用增强,进而促进了胸径和树高生长。本研究对叶表面积密度x的灵敏度分析结果表明,叶表面积密度x对胸径和树高生长影响较低,树冠树叶分形维数z的影响则高于叶表面积密度x(表5),与欧洲赤松的CROBAS模型灵敏度分析结果类似(Mäkelä, 1997)。因为树冠树叶分形维数z是异速生长方程中的指数,其不仅影响叶生物量曲线,还影响该曲线的形状。 本研究的CROBAS模型是与年龄无关(age-independent)的林分生长模型,因而可用于模拟复层或混交林生长动态(Minunnoetal., 2019)。然而,这种与年龄无关的模型,通常无法描述树木衰老引起的生理组织代谢速率和碳利用效率的改变。Vanninen等(1996)对欧洲赤松林木(18~212年生)生物量的研究显示,细根与叶生物量在树木整体生物量的相对占比随年龄增加而减小,而与此同时,细根与叶生物量比值会随年龄增大而增大,本研究中参数细根与叶生物量比值和细根衰老速率对胸径与树高预测的全局灵敏度值相对较低(表5),因而未设定其与年龄的关系,但这种与年龄无关(age-independent)的模型简化会导致对不同龄级林木细根生物量估计的误差。因此,在构建与年龄相关(age-dependent)的生长模型时,应补充考虑这种变化。 本研究通过参数优化模型调试CROBAS过程模型参数,基于经验模型和过程模型的混合建模方法构建了华山松过程模型CROBAS-PA。研究表明,经过生物量异速生长方程和全林经验模型约束的华山松过程模型CROBAS-PA,可准确预测林分树高和胸径生长及林木各器官中的生物量分配。全局灵敏度分析显示,在CROBAS-PA模型参数中,比叶面积An、最大光合速率P、消光系数k和树冠树叶分形维数z的敏感度较高。研究证明,在有限实测数据和文献信息条件下,可在林分水平上通过经验模型约束保证过程模型预测的准确性。这意味着对于数据缺失情境下的复杂过程模型的参数预估,这种经验-过程混合建模方法有着特定的优势与应用潜力。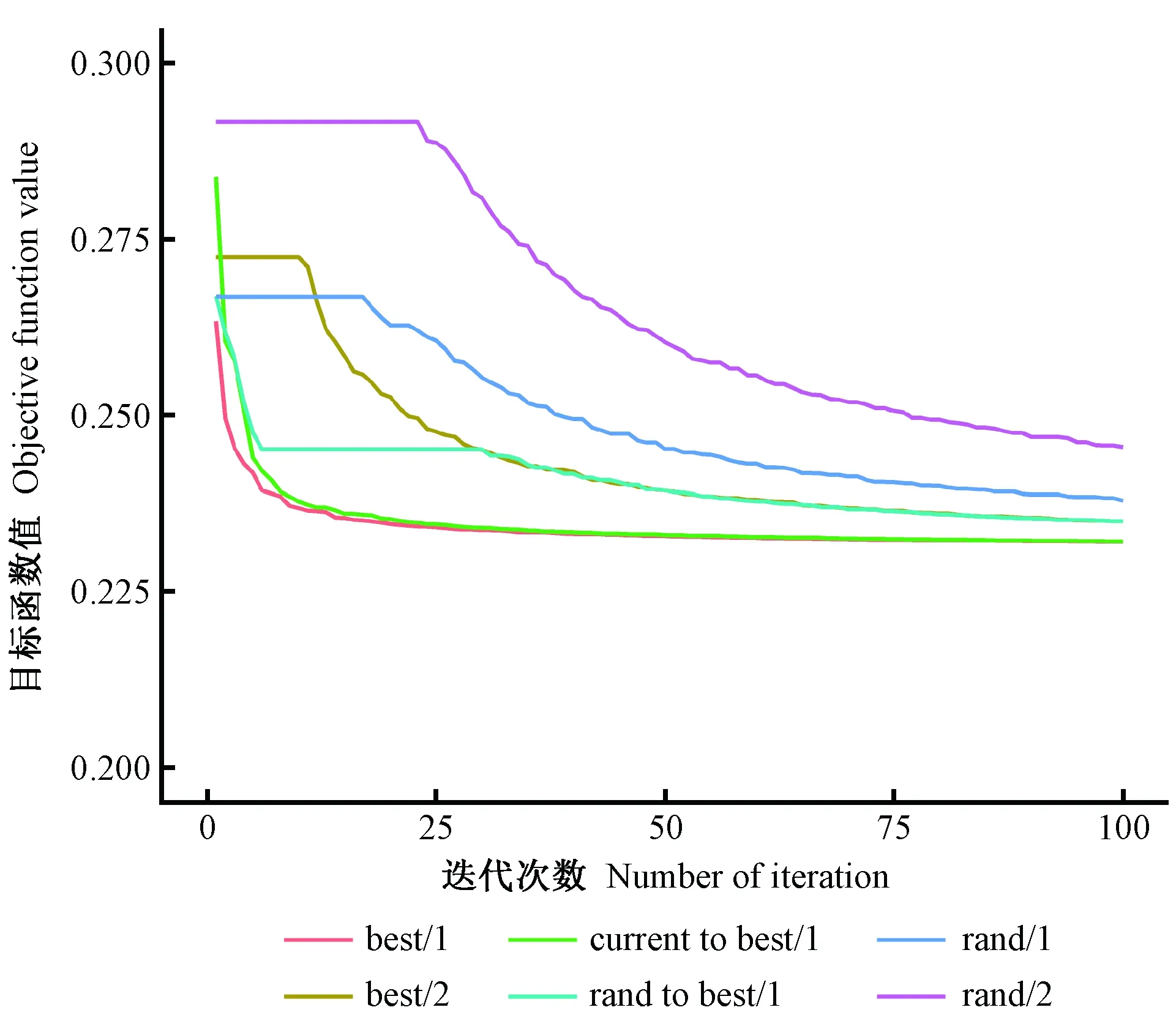
2.5 模型检验及敏感性分析
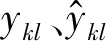
3 结果与分析
3.1 过程模型参数本地化
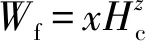
3.2 过程模型与经验模型比较
3.3 预测误差与参数敏感性


4 讨论
5 结论

