钢管-角钢组合输电塔杆件体型系数及背风面风荷载折减系数的风洞试验研究

牛华伟，刘淦彬，杨风利，张宏杰

（1.湖南大学 土木工程学院，湖南 长沙 410082；2.中国电力科学研究院有限公司，北京 100055）

输电塔由于自身独特的结构，对风荷载极其敏感，因此对于不同结构形式的输电塔风荷载计算和参数运用是必不可少的.体型系数和背风面风荷载折减系数是输电塔风荷载中的关键参数.近年来，钢管-角钢组合输电塔的运用越来越广泛，而对钢管-角钢组合输电塔的风荷载研究却很少.

目前，国内外针对输电塔等格构式结构的风荷载研究主要为测力[1]和测压[2]风洞试验.孙远等[3]通过高频天平测力试验得到了不同湍流度下格构式塔架的静力风和脉动风荷载.楼文娟等[4]对角钢塔身节段模型进行某一风速下的测压试验，获得了角钢杆件和节段模型的体型系数，改进了JEC 总计法的参数.杨风利[5]通过测力试验分析，得到3 个风速下两个角钢横担节段模型阻力系数，发现风速对角钢横担的阻力系数影响很小.Mara 和Ho[6]采用横担与塔身组合模型的测力试验，认为横担的气动特征较塔身复杂，美国规范得到垂直于线路方向的风荷载较小.卞荣等[7]通过不同的密实度、高宽比、湍流度的钢管塔身节段模型和单片桁架模型的测力试验，得到了节段模型体型系数和背风面风荷载折减系数.李正等[8]对某一典型钢管-角钢组合塔身进行两个风速下0°～90°风向角的测力试验，识别了不同风向角的阻力系数.杨风利等[9]筛选出有代表性的角钢和双拼角钢并对其进行不同间距比杆件遮挡测力试验，获得输电塔角钢杆件在空风场下的阻力系数和背风面风荷载折减系数，但是试验结果忽略了杆件及塔架整体的三维扰流影响.

国外规范[10-15]中除日本规范单独给出了横担结构的体型系数计算公式外，其他国家对于横担和塔身体型系数计算公式是相同的.中国规范[16]的体型系数计算公式主要通过背风面风荷载折减系数来体现，但是规范并未对角钢和钢管的折减系数进行区分.杨风利等[17]在塔身单片桁架测力试验中，发现角钢和钢管-角钢组合塔身的折减系数试验值较规范值低，钢管塔身的折减系数试验值与规范值较为接近.钢管和角钢的体型系数区别较大，背风面风荷载折减系数也有一定区别.国内外通过天平测力试验研究输电塔的体型系数，只能测得整体结构的气动力，无法获得杆件风荷载分布.对于高耸输电塔的杆件，不同位置风荷载不同，断面较小时，安全富余度不大，需准确计算风荷载.横担做测力试验时，需测得塔身和横担总力，再扣除塔身所承担的力，两次试验累计了更多误差.通过风洞测压试验研究塔身及横担的单根杆件体型系数和背风面风荷载折减系数时，杆件受到空间桁架节段中其他杆件的三维扰流影响，试验结果更有参考意义和运用价值.

本研究以500 kV 和110 kV 钢管-角钢组合输电塔为原型，考虑到钢管体型系数受雷诺数的影响，分别取一段塔身和横担进行3 个风速下的风洞测压试验，获得3 个风速下不同风向角的杆件体型系数及其风荷载分布，计算得到杆件和节段模型的背风面风荷载折减系数、单片桁架和节段模型的体型系数，并与各国技术标准进行比较分析.试验结果可为基于单根杆件到整体输电铁塔及其他高耸桁架结构的风荷载精细化计算提供参考.

1 风洞试验

1.1 工程背景

塔身和横担原型分别取自某500 kV 和110 kV高压钢管-角钢组合输电塔，其所处的区域均在海岸线附近，风环境复杂，大风天数多.因此根据横担和塔身的杆件特征，选取图1 框中塔身和横担为试验模型.

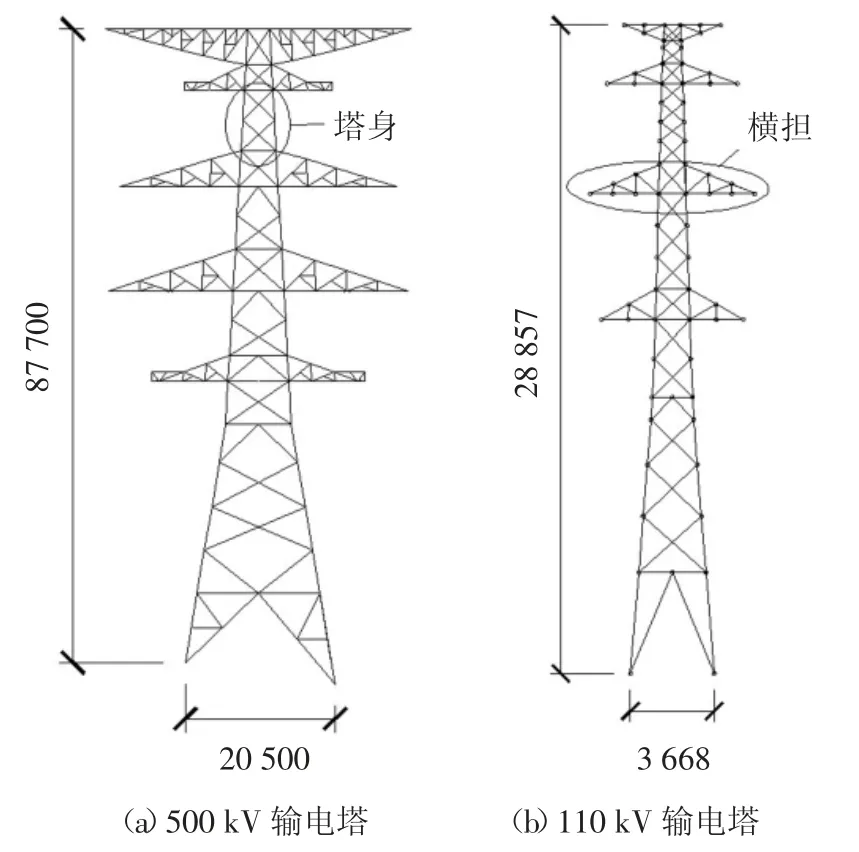
图1 钢管-角钢组合输电塔原型（单位：mm）Fig.1 Prototype of tubular-angle steel transmission towers（unit：mm）

1.2 节段模型设计

为保证模型能牢固安装，满足阻塞比5%等要求，设计塔身模型缩尺比为1 ∶8.5，横担模型缩尺比为1 ∶2.5.由于测压孔直径的限制，角钢杆件的肢厚很难按照比例缩尺，因此塔身和横担的角钢肢厚均设为4 mm.塔身缩尺后的钢管直径为45 mm，角钢肢宽为24 mm，横担缩尺后的钢管直径为80 mm，角钢肢宽18 mm.模型钢管和角钢分别用有机玻璃和ABS 板制作而成.塔身和横担节段模型密实度分别为0.300 和0.493，其钢管迎风投影面积占比分别为56.8%和87.0%.为消除风洞底部边界层的影响，模型下部连接一个20 cm 高的底座.整个模型装置安装在风洞转盘上，转动转盘获取不同的风向角.节段模型安装试验如图2 所示.

图2 风洞试验照片Fig.2 The photos of wind tunnel tests

由于塔身和横担都为双轴对称图形，测压点布置在模型迎风面和背风面的各一半，侧面角钢不布置测压点.角钢尺寸较小，考虑测压孔布置可行性，每个角钢测压层截面布置12 个测压孔.钢管测压层截面一周均匀布置20 个测压孔.当风向角为0°时，同一高度迎背风面的测压层是顺线向平行对应.横担和塔身节段模型的测压层布置位置及测压层截面测孔布置情况如图3 所示，其中GA、GB 和JA～JH为测压层，具体含义见表1（相对应的迎背风面杆件代号和编号一致）.塔身共布置352 个测压点.横担共布置376 个测压点.模型底部连接底板，测压管设置在角钢和钢管内部，顺杆件传至底板下方，防止测压管对杆件风荷载的影响.

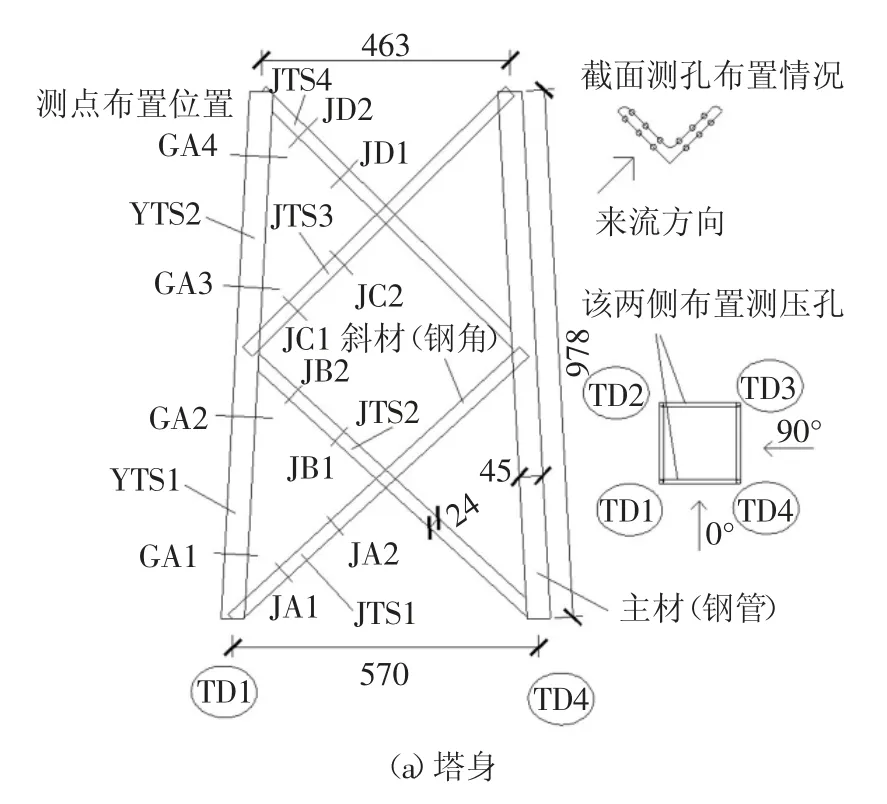
图3 节段模型测压层及详细测点布置Fig.3 Layout of pressure measuring points of section model

表1 输电塔角钢和钢管杆件编号Tab.1 No.of steel pipe and angle members

试验在中南大学风洞试验室高速试验段中进行，风洞宽3 m，高3 m，长15 m.测试风场为均匀流场，湍流度不超过0.2%.测压仪器为PSI 扫描阀，用澳大利亚TFI 公司的三维眼镜蛇探针测来流风速.风向角正对模型TD1、TD4 面时，阻塞比均小于5%.塔身节段模型试验风速为10.0 m/s、12.5 m/s、15.0 m/s，横担节段模型试验风速为10.1 m/s、12.6 m/s、14.5 m/s，两者的主材雷诺数都处于亚临界区间.试验风向角为0°～90°，每隔5°转一个风向角.

1.3 数据处理

每个测压点的风压系数：

式中：i 为测压点编号；Cp（i）为第i 个测压点的风压系数；p（i）为i 点处的风压；pr为参考点风压；ρ 为来流空气密度；vr参考点风速.

角钢和圆管每个测压层可以采用表面积分法得到风轴下体型系数，计算公式为：

式中：CD为测压层风轴下的阻力系数；CL为测压层风轴下的升力系数.di为测点i 所占的计算长度；d为测压层一周的计算长度；n 为测压层的测压点数；Cp（i）为测压层第i 个测压点的风压系数；αi为测压点所在杆件面的法线的水平投影与来流反向的夹角；βi为测压点所在杆件面的法线与水平面的夹角.

2 体型系数分析

2.1 角钢杆件体型系数与风速

限于篇幅，取塔身与横担各2 个角钢测压层，其体型系数随风向角的变化曲线分别如图4 和图5 所示.由图4、图5 可知，同一角钢测压层3 个风速下的体型系数随风向角的变化曲线几乎重合，来流风速变化对输电塔中角钢的阻力系数和升力系数几乎无影响，此结论验证了杨风利等[9]的结论.在背风面，由于迎风面杆件的干扰造成来流湍流度更大，此时不同风速体型系数随风向角的变化曲线也几乎重合.同一杆件的不同测压层的体型系数随风向角的变化曲线基本一致.同一风向角的不同测压层体型系数基本重合，表明体型系数沿角钢杆件的分布比较均匀，其中塔身曲线重合度更高.

图4 塔身同一角钢不同测压层3 个风速下体型系数随风向角变化曲线Fig.4 Variation curves of the shape coefficient with wind incidence angles under three wind speeds for the same angle of tower body with different pressure measuring sections

图5 横担同一角钢不同测压层3 个风速下体型系数随风向角变化曲线Fig.5 Variation curves of the shape coefficient with wind incidence angles under three wind speeds for the same angle of cross-arm with different pressure measuring sections

2.2 角钢杆件体型系数与风向角

同个角钢的不同风速下的不同测压层的体型系数变化曲线基本一致，因此把同个角钢的不同测压层不同风速的体型系数进行平均，得到单根角钢杆件的体型系数随风向角变化曲线，如图6 和图7 所示.

图6 角钢迎风面体型系数随风向角变化曲线Fig.6 Variation curves of the shape coefficient of windward side of angle with wind incidence angles

图7 角钢背风面体型系数随风向角变化曲线Fig.7 Variation curves of the shape coefficient of leeward side of angle with wind incidence angles

由图6 和图7 可知，无论在塔身还是横担中，角钢L 型朝向的不同，造成体型系数随风向角的变化趋势不同，体型系数主要有两种变化趋势.塔身和横担中的角钢摆放角度相似的，其体型系数随风向角变化曲线也是相似的.塔身的角钢空间位置更加相似，其变化趋势也更相近.当风向角在10°左右时，塔身和横担角钢的迎风面阻力系数和背风面升力系数都处于较大值.

表2 为0°风向角的横担和塔身的角钢体型系数.迎风面的塔身角钢阻力系数均值为1.77，横担角钢阻力系数均值为2.05，相对于ASCE 和AS 规范的2.0 规范值，分别相差-11.5%和2.5%，与杨风利等[9]试验提出1.93 的推荐值，分别相差-8.3%和6.2%.塔身角钢阻力系数较小，由于其长细较小，有末端效应[14].ASCE 规范提出0.3 的升力系数规范值，试验中只有JHD3 的升力系数为0.3，其他角钢升力系数均在0.1 左右.

2.3 钢管杆件体型系数与风速、风向角

钢管杆件阻力系数随风向角的变化曲线如图8所示，图例的V1、V2和V3代表试验从小到大的3 个来流风速.在0°风向角下，塔身和横担的迎风面的钢管阻力系数分别处于0.97～1.13 和0.90～1.05 之间，小于单圆柱阻力系数规范取值[14]的1.2.不同风速下迎风面的塔身和横担钢管测压层阻力系数曲线较为集中，而背风面测压层的阻力系数曲线较为分散.这主要是由于迎风面钢管几乎只有雷诺数不同，而对于背风面钢管，来流受迎风面杆件干扰造成其湍流度也不同，因此不同风速的阻力系数曲线较为分散.

图8 钢管杆件阻力系数随风向角变化曲线Fig.8 Variation curves of the drag coefficient of steel pipe with wind incidence

塔身钢管近似垂直于地面，当风向角大于80°，迎风面钢管被其他杆件遮挡，阻力系数不断减小.横担钢管由于倾斜角较大，当风向角由0°增加到90°时，测压层受到自身钢管和其他杆件的影响，阻力系数越来越小.

2.4 迎背风面钢管与串列双圆柱的阻力系数对比

对于钢管-角钢组合输电塔结构，在0°风向角时，来流经过迎背风面的两根钢管，此时钢管类似串列双圆柱绕流.塔身和横担钢管与铅垂面有2°～3°夹角，因此不同高度的迎背风面钢管测压层的间距不同.将本试验结果与国内外的串列双圆柱绕流试验结果进行对比，如图9 所示，其中横坐标s 为相对应的迎背风面测压层圆心间距和直径的比值，图例的塔身或横担雷诺数指的是塔身或横担的钢管处于该雷诺数下得到的试验值.实心和空心图例分别代表上、下游圆柱.

图9 0°风向角下钢管迎背风面阻力系数Fig.9 Drag coefficients of windward and leeward side of steel pipe under 0°incidence angle

郭明旻[18]和杨群等[19]通过均匀流中的测压试验得到参考文献数值，Alam 等[20]通过测力试验得到参考文献值.横担和塔身钢管上游的阻力系数处于0.90～1.13 之间，与杨群等的结果较为接近.横担钢管下游的阻力系数在0.25～0.45 之间，都处于参考文献的试验值范围内.塔身钢管下游阻力系数处于0.39～0.57 之间，比杨群等的试验值（0.38～0.43）稍大.

2.5 节段模型体型系数

为了解钢管-角钢组合输电塔整个塔段的风荷载分布规律，将0°风向角下的钢管和角钢各测压层的体型系数绘制到塔身和横担节段立面图上，取最大风速下的杆件体型系数，如图10 和图11 所示.

图10 0°风向角塔身各杆件下体型系数分布Fig.10 Distribution of the shape coefficients of each member in tower body under 0°incidence angle

图11 0°风向角横担各杆件下体型系数分布Fig.11 Distribution of the shape coefficients of each member in cross-arm under 0°incidence angle

由图10 可看到：1）总体上，角钢（斜材）阻力系数约为钢管（主材）阻力系数的两倍；2）阻力系数在迎背风面钢管沿杆件展长的分布趋势不同，在迎风面呈上小下大分布，在背风面呈中间大两端小分布；3）角钢的体型系数在迎背风面节段都呈上小下大的变化趋势，造成该现象的原因可能是由于输电塔塔身立面呈梯形，在下部的角钢杆件长细比比上部的角钢大；4）角钢的迎风面升力系数几乎为0，而背风面升力系数极大.背风面角钢L 型内角迎风，出现局部兜风效应[2]，此时其升力和阻力系数均较大.

由图11 可知：1）横担迎风面钢管阻力系数分布规律与塔身相同，都为沿杆件呈上小下大分布，但在背风面钢管则呈上大下小分布；2）横担的钢管直径与角钢肢宽相差较大，由于钢管对来流风的遮挡，对邻近的角钢来流起到了一定的削弱作用，因此靠近横担整体形心（对于一侧横担）位置的角钢体型系数较大，而靠近钢管位置的角钢体型系数较小；3）与塔身相似，横担背风面角钢也有局部兜风效应.

将各个杆件体型系数取杆件迎风面积的加权平均值作为整体节段的体型系数.由于结构轮廓变化较大的部位，如杆件连接处，往往很难布置测点，测压结果忽视了该部分的风荷载信息，因此该均值相较于真实值有误差.表3 为0°风向角下节段模型在最大风速中的阻力系数值国内外规范值的对比情况.美国、日本规范值与塔身试验值较吻合，而且日本规范值与横担试验值也较吻合.对于塔身规范值，除日本和美国规范外，其他规范值在1.95～1.99 之间，差值均为-7%左右.对于横担规范值，除日本规范外，其他规范差值均在-5%～-8%之间.除日本的其他规范值，相对于塔身和横担的试验值都偏不安全各国家和地区.

表3 0°风向角下节段模型阻力系数与不同规范值对比Tab.3 Comparison of drag coefficients of section models under 0°incidence angle with some standard values

3 背风面风荷载折减系数与不同规范对比

3.1 角钢杆件背风面风荷载折减系数

图12 为本试验角钢背风面风荷载折减系数和参考文献值的对比情况.0°风向角下单根杆件背风面三风速的阻力系数均值与迎风面阻力系数均值的的比值为角钢背风面风荷载折减系数.角钢遮挡距离与迎风面杆件宽度（肢宽）的比值为s.杨风利等[9]和Prud′homme 等[21]的杆件背风面风荷载折减系数都是通过测力试验获得.塔身角钢折减系数与参考文献都较为吻合，其中杨的最为接近，主要原因是杨的迎背风面角钢的L 型朝向角度与输电塔中的相同，而Prud′homme 等是角钢不同L 型朝向角度曲线再拟合的.横担角钢折减系数比较分散，远离横担形心（横担的一侧）的最外两根角钢（JHD1 和JHD4）折减系数比参考文献值偏小，比JEC 分别偏小16.1%和42.0%.

图12 角钢杆件背风面风荷载折减系数Fig.12 The shielding factors of angle members in tower body and cross-arm

3.2 钢管杆件背风面风荷载折减系数

计算0°风向角迎背风面输电塔钢管测压层阻力系数的比值，获得钢管背风面风荷载折减系数，如图13 所示，其中s 为对应的迎背风面测压层圆心间距和直径的比值.由图13 可知，试验值均在参考文献范围内.无论在塔身还是横担中，s 相近的钢管折减系数差值较大，图中试验值斜率均大于参考文献值斜率.塔身钢管折减系数比JEC 规范值偏小，横担靠下部的钢管折减系数与JEC 较吻合.类似参考的3种雷诺数下折减系数在亚临界区间，同一s 下，钢管折减系数均随雷诺数的增大而减小.

图13 钢管杆件背风面风荷载折减系数Fig.13 The shielding factors of steel pipe members in tower body and cross-arm

3.3 节段模型背风面风荷载折减系数

表4 为不同雷诺数下0°风向角塔身和横担的迎背风面单片桁架阻力系数和背风面风荷载折减系数，并与不同规范值的对比情况.

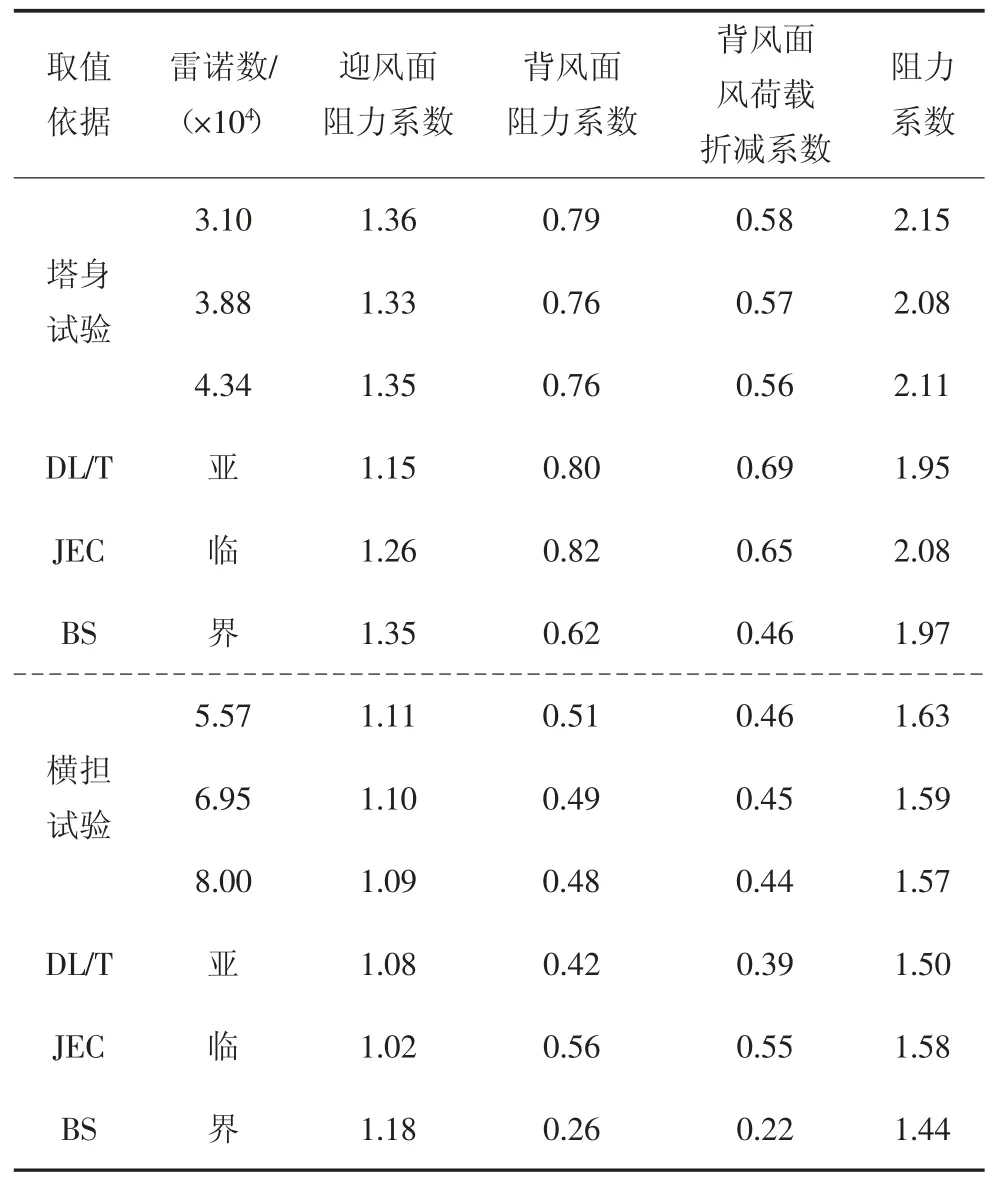
表4 0°风向角塔身和横担节段模型不同雷诺数下背风面风荷载折减系数Tab.4 The shielding factors of tower body and cross-arm section models with different Reynolds numbers under 0°incidence angle

由表4 可知，不同雷诺数下（本试验中）的单片桁架阻力系数和节段模型背风面风荷载折减系数的差值很小，节段模型的阻力系数也相差不大.塔身和横担的中国规范折减系数与试验值分别相差19.0%和-13.3%.日本规范（JEC）的折减系数较试验值大，而英国规范（BS）的折减系数较试验值小.英国规范的塔身单片桁架迎风面阻力系数和中国规范（DL/T）的横担单片桁架迎风面阻力系数都与试验值较为吻合.

4 结论

通过对钢管-角钢组合塔身和横担节段模型进行风洞测压试验，获得了3 个风速下塔身和横担迎背风面不同风向角下的角钢和钢管杆件体型系数，分析了单根杆件和节段模型的背风面风荷载折减系数，得到如下结论：

1）均匀流场下，来流风速对塔身和横担中的角钢体型系数几乎无影响.0°风向角下，塔身和横担中的角钢迎风面阻力系数均值分别为1.77 和2.05，与ASCE 和AS 规范值的2.0，分别相差-11.5%和2.5%.均匀流场雷诺数处于亚临界区间，风向角为0°时，塔身和横担中的钢管迎风面阻力系数分别处于0.97～1.13 和0.90～1.05 之间.

2）在0°风向角下，塔身角钢体型系数沿塔身节段呈上小下大变化.

3）0°风向角下塔身和横担节段模型阻力系数与日本规范取值吻合，本国规范取值分别偏小7.2%和4.5%.

4）塔身中的角钢背风面风荷载折减系数与JEC较吻合，远离横担（一侧）形心的角钢折减系数较JEC 分别小16.1%和42.0%.

5）在不同雷诺数下，塔身（3.10×104～4.34×104）或横担（5.57×104～8.00×104）节段模型背风面风荷载折减系数的差值很小，阻力系数也相差不大.