基于改进损伤算法及MCMC 车流模拟的混凝土桥梁疲劳寿命预测

王俊峰，黄平明†，韩万水，袁阳光，周广利，许昕

（1.长安大学 公路学院,陕西 西安 710064；2.西安建筑科技大学 土木工程学院,陕西 西安 710055；3.山东省交通科学研究院,山东 济南 250014）

截至2019 年末，全国公路桥梁已达87.83 万座，其中超过90%为混凝土桥梁.随着公路交通运输荷载的提高与运输频次的增加，公路混凝土桥梁承受着日以万计的车辆疲劳荷载作用，部分混凝土桥梁长期处于高应力工作状态，出现开裂、保护层剥落、钢筋锈蚀等病害，对混凝土桥梁的耐久性与安全性造成了极大的危害.为保障桥梁安全，避免潜在事故，在役混凝土桥梁疲劳寿命预测已成为当下的研究重点之一[1].混凝土桥梁疲劳寿命预测取决于两方面：1）预测准则的选择；2）应力幅谱的获取.

疲劳寿命预测准则是混凝土桥梁疲劳寿命预测的核心.诸多学者相继提出了Palmgren-Miner 线性累计损伤准则[2]（以下简称P-M 准则）、Marco-Starkey 模型[3]、Manson 双线性准则[4]、Corten-Dolan准则[5]等，其中Marco-Starkey 模型与Manson 双线性准则计算过程复杂，Corten-Dolan 准则相关参数变异性较大[6-7]，未能大范围应用.P-M 准则是工程领域预测疲劳寿命应用最广泛的准则，诸多学者应用其对混凝土桥梁的疲劳寿命进行了研究.Pimentel 等[8]、Xin 等[9]、黄华等[10]、张劲泉等[11]、邓露等[12]基于P-M准则，通过数值模拟的方法计算了标准疲劳车辆与随机车流下公路混凝土桥梁的疲劳寿命.孙晓燕等[13]、刘扬等[14]利用P-M 准则分析了车辆超载对钢筋混凝土简支梁桥疲劳寿命的影响.赵尚传等[15]基于P-M 准则建立混凝土结构疲劳寿命的极限状态方程，分析了不同加载频率下结构的疲劳可靠性及疲劳寿命.王春生等[16-17]基于P-M 准则与断裂力学方法，利用桥梁应力监测数据对不同截面类型的现役混凝土桥梁进行了疲劳寿命预测.李岩等[18]基于PM 准则提出了装配式混凝土梁桥横向联系的疲劳评估方法和框架.然而由于损伤累计算法的简化，使得P-M 线性准则虽然在操作上比较简便，但预测结果与真实寿命存在一定的差距，因此需要对损伤累计的计算方法进行修正.

获取准确的应力幅谱，最直接的手段是在目标桥梁上安装健康监测设备，获取目标桥梁的应力时程曲线[19]，但一般中小桥未配备监测系统，因此，在预测混凝土桥梁疲劳寿命时，随机车流模拟加载是学者们常采取的研究方法.韩万水等[20-22]首次将车型、车速、车重、车距等参数全面引入随机车流生成中，并进一步将微观元胞自动机（Cellular Automaton，CA）交通流模拟方法与Monte-Carlo 法相结合，建立了更加完整的交通流模型.程高等[23]、刘扬等[24]、王涛[25]、阮欣等[26]、殷新锋等[27]、Yu 等[28]也基于Monte-Carlo 法进行了多车道随机车流的模拟.林诗枫等[29]将车辆到达相关性引入随机车流生成中，产成的车流更加贴近真实状况.综上可知，车流模拟精细化程度不断提高，但混凝土桥梁疲劳寿命相关预测研究[8-14]均对随机车流模拟进行了不同程度的简化，如不考虑车道分布的差异性、忽略车队序列之间的相关性等，将对预测结果造成一定的影响.

本文提出一种基于改进损伤算法[30]及多车道精细车流模拟的混凝土桥梁疲劳寿命预测方法，利用一组钢筋混凝土空心板、T 梁变幅疲劳试验，验证了改进损伤算法对于混凝土梁桥疲劳寿命预测的准确性，并利用实测车流统计数据生成一组多车道随机车流，分析了一座钢筋混凝土简支T 梁桥的疲劳寿命，以期为混凝土桥梁疲劳寿命预测方法提供新的研究思路.

1 改进损伤算法及其验证

1.1 改进损伤算法

1.1.1 P-M 准则

20 世纪20 年代，Palmgren 第一次提出了基于线性准则的疲劳损伤累计原则.随后于1945 年，Miner将疲劳损伤量定义为D，并规定当损伤量D 达到1时，材料发生疲劳破坏，由此形成了P-M 准则，其数学形式为：

式中：D 为损伤累计量；ri为第i 个应力水平所造成的损伤百分比；ni为与第i 个应力水平相对应的循环次数；Nf，i为第i 个应力水平相对应的单级疲劳下的疲劳寿命，可由单级疲劳试验或者S-N 曲线得出.

1.1.2 损伤材料的S-N 曲线

对同一种材料进行多次不同应力水平S 下的单级等幅疲劳试验，得到多个疲劳寿命值N，两者之间存在固定的函数关系，即为S-N 曲线，表达式为：

两边同时取对数，S-N 曲线的线性表达式为：

式中：S 为应力幅值；N 为疲劳寿命；C 和m 为材料常数，可由试验获得.

在S-N 曲线中，m 为疲劳强度指数，是与构件疲劳细节相关的参数，根据统计分析[31]发现，对于同一种材料，m 值的波动很小，因此，对于同一种材料，m可认为是不变的.但C 值随样本的波动较大，材料内部的杂质以及初始缺陷会导致材料的初始状态发生改变，影响材料的疲劳性能.因此，可以认为C 值是与材料状态密切相关的参数，随着材料损伤的累计，应对C 值加以修正.

修正后的C 值与每一级荷载对材料造成的损伤相关，关系式为：

式中：Ci、Ci-1分别为第i 级荷载和第i-1 级荷载作用下材料的C 值；Di-1为第i-1 级荷载作用下材料的损伤值，可由Di-1=ni-1/Nf，i-1得出，ni-1为第i-1 级荷载作用下的循环次数，Nf，i-1为第i-1 级荷载作用下的单级等幅疲劳寿命.

因此，损伤材料的S-N 曲线表达式为：

式中：Nf，i为第i 级荷载作用下的单级等幅疲劳寿命.

对两边取对数，可得

1.1.3 改进损伤算法及疲劳寿命预测流程

通过计算材料的S-N 曲线，对材料累计疲劳损伤的算法进行修正，修正后即可通过改进损伤算法进行材料疲劳寿命的预测.对于一般的变幅疲劳加载而言，通常基于一个加载块进行变幅加载直至试件破坏，设一个加载块中应力幅的个数为Nblock，则改进损伤算法预测材料疲劳寿命的具体流程如图1所示.

图1 改进损伤算法及预测流程Fig.1 Improved damage algorithm and prediction process

1.2 改进损伤算法试验验证

带筋混凝土结构作为一种复合材料构件，有2种疲劳破坏模式：一是混凝土疲劳破坏；二是钢筋疲劳破坏.因此，需要确定哪种破坏方式占主导地位，文献[32]指出公路钢筋混凝土受弯梁在重复荷载作用下，适筋梁的疲劳破坏模式主要为钢筋的疲劳破坏，即带筋混凝土构件的疲劳寿命主要由钢筋控制，这一结论在国内外带筋混凝土疲劳试验中得到验证[6，32-33]，故可将带筋混凝土桥梁的疲劳寿命转换为梁体内受拉主筋的疲劳寿命，本文改进损伤算法的验证与应用均基于此结论展开.

公路桥梁承受的疲劳荷载幅为车辆荷载反复作用产生的结果，其疲劳荷载为多级变幅荷载.混凝土试件疲劳试验成本较高，为最大限度挖掘已有试验成果资源，选取一组钢筋混凝土梁[33]与预应力混凝土梁疲劳试验[6]对改进损伤算法进行验证.

1.2.1 钢筋混凝土梁疲劳试验

1）疲劳试验内容及结果

朱红兵[33]分别浇筑钢筋混凝土空心板梁与T 梁试件各9 片，用于静载破坏试验、等幅疲劳试验与多级变幅疲劳试验，试验梁模型参照实桥进行缩尺，空心板梁与T 梁试件的尺寸、材料特性见表1.

表1 试件尺寸、材料Tab.1 Specimen size and material

在室内进行疲劳试验时，为便于控制试验进程和适应MTS 试验机的特性，以一个荷载块作为一个加载周期，每一加载块包含由10 级加载等级组成的1 000 次循环荷载，这样处理加载方式虽然不是严格意义上的随机变幅荷载，但其控制简便，而且从试件的疲劳寿命尺度（百万次）讲，加载谱可认为是随机加载.此外，如此加载应力时程呈现周期性变化，对于验证改进损伤算法提供了极大便利.单个加载块荷载见表2，多级变幅试验加载示意图如图2 所示.混凝土试件疲劳破坏的标志通常为普通钢筋的疲劳断裂，因此钢筋混凝土试件中钢筋的疲劳寿命即为钢筋混凝土试件的寿命.多级变幅疲劳试验的试验结果为：空心板的疲劳寿命为110 万次，T 梁的疲劳寿命为137.8 万次.

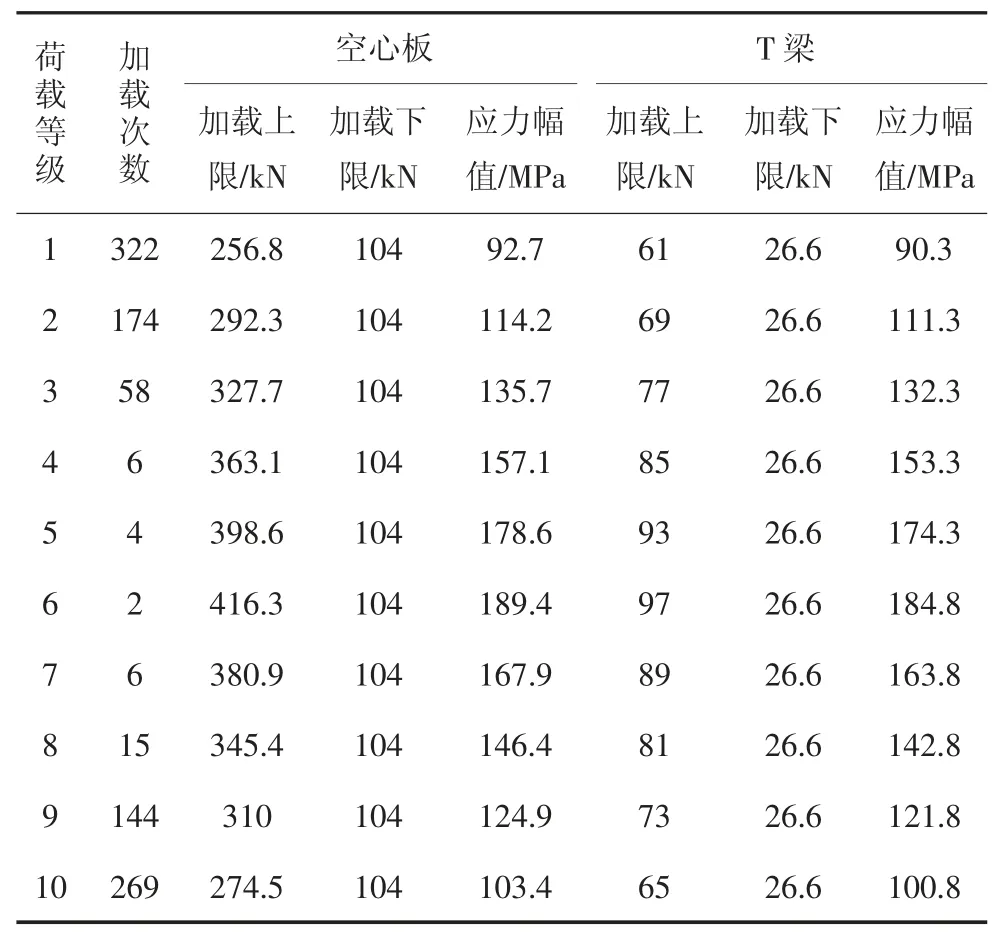
表2 单个加载块荷载Tab.2 A single loading block

图2 多级变幅试验加载示意图[33]Fig.2 Schematic diagram of multi-stage variable amplitude test loading[33]

2）改进损伤算法结果检验

文献[33]通过10 组钢筋混凝土试件等幅疲劳试验结果拟合得到了如下S-N 曲线：

式中：C=1012.8；m=3.191 1.

依据改进损伤算法疲劳寿命预测流程，在MATLAB 中进行全过程疲劳损伤及寿命预测.作为比较，同时计算了常规损伤算法的预测结果.常规损伤算法与改进损伤算法全过程损伤进程如图3 所示.

图3 全过程损伤进程Fig.3 Damage process of the whole process

从图3 中可以看出，常规损伤算法的损伤增长速度全程无明显增加，而改进损伤算法的损伤增长速度随疲劳加载的进程逐渐加快.各曲线与D=1 的交点横坐标即为试验梁的预测寿命.常规损伤算法及改进损伤算法的预测寿命见表3.

表3 不同方法预测钢筋混凝土梁疲劳寿命Tab.3 Prediction of fatigue life of reinforced concrete beams by different methods

从表3 可以看出，常规损伤算法的预测误差为45%～69%，改进损伤算法的误差不到8%，大幅减小了预测误差.

1.2.2 预应力混凝土梁疲劳试验

1）试验内容及结果

冯秀峰[6]完成了一组17 根混合配筋的预应力混凝土T 梁的等幅及变幅疲劳试验，其中包括3 根随机变幅疲劳试验，17 根预应力混凝土T 梁试件根据配筋情况分为3 组，3 组随机变幅试件编号分别为B1、B2、B3.混凝土立方体抗压强度平均值为64 MPa，普通受拉钢筋采用HRB400 级钢筋，预应力筋采用1860 级钢绞线，疲劳试验采用与1.2.1 节中类似的加载块的形式进行加载，单个加载块共20 级荷载，单个加载块的详细情形如图4 所示.图4 中Mu为加载上限值与试件静载试验极限抗弯承载力之比，3 组试件的静载抗弯承载力分别为170.5 kN·m、244.8 kN·m、269.0 kN·m.

需要指出的是，为增加随机性，原试验在加载过程中对单个加载块中各级荷载打乱了次序，并不是按照图4 所示由小到大的顺序，本文假定其按照图4由小到大的顺序进行加载.

图4 单个加载块示意图Fig.4 Diagram of a single loading block

3 组变幅试验构件的破坏类型均为纯弯段普通钢筋首先发生疲劳断裂，疲劳寿命分别为17.4 万次、39.2 万次、14.9 万次.

2）改进损伤算法结果检验

文献[6]通过等幅疲劳试验得到了混凝土中钢筋的S-N 曲线为：

同样利用改进损伤算法和常规损伤算法，计算3组随机变幅试验构件的疲劳寿命，常规损伤算法及改进损伤算法的预测寿命见表4.

表4 不同方法预测预应力混凝土梁疲劳寿命Tab.4 Prediction of fatigue life of prestressed concrete beams by different methods

从表4 可以看出，利用常规损伤算法时B1～B3的预测误差为30.37%～72.30%，改进损伤算法的误差为7.69%～56.18%，较常规损伤算法有明显下降，较1.2.1 节中钢筋混凝土疲劳试验误差大.分析其原因，可能是原试验加载块的随机性，导致原试验的加载顺序与本文验证时所采取的加载顺序不一致，且试件本身的随机性对结果也会产生一定的影响.

综合1.2.1 节与1.2.2 节的验证结果，5 组试件预测误差较常规损伤算法均有明显降低，除2 根预应力混凝土梁预测误差较大（53%～56%）外，其余3 组试件误差较小（小于8%），利用本文所提出的改进损伤算法能较大提高预测精度，因此该方法可用来预测带筋混凝土桥梁的疲劳寿命.

2 MCMC 多车道随机车流模拟方法

疲劳试验中，施加在试验梁上的荷载分为等幅荷载及随机变幅荷载，等幅荷载是为了获得试验梁的S-N 曲线，随机变幅荷载采取与真实荷载较接近的疲劳荷载.对于公路混凝土桥梁而言，直接承受的是往复行驶的车辆荷载，在疲劳试验中相当于随机变幅荷载.

利用实测交通数据拟合车辆荷载参数，通过蒙特卡洛（M-C 抽样）模拟随机车流是常用的生成桥梁汽车荷载样本的方法.多车道随机车流生成包含几个重要参数：车道选择、车辆到达、各车型质量、纵向轴距、轴重及车间距.根据交通数据可以对上述参数进行分布拟合，拟合手段包括参数化拟合和非参数化拟合2 种方法，其中参数化拟合对于抽样的精度及速度有利，但经常遇到参数化拟合程度较低或参数不易获取的情况.非参数化拟合常用核密度估计法.

车型质量、纵向轴距、轴重及车间距等不随时间变化的参数模拟在既有文献中介绍较多[18-27]，在此不再赘述.对于车道选择及车辆到达等时变参数，较多的研究中仅对各车道及各车型的比例因子进行抽样，忽略了车辆达到的相关性.文献[34]中指出车辆达到的序列符合马尔科夫链的特征，即一个状态空间中某一时刻的状态只与上一时刻t0相关，与t0之前的状态无关.同理，本文经过大量抽样试验，证明车道选择序列同样符合马尔科夫链的特征，这一结论在4.2 节车辆荷载模型中得到了验证，限于篇幅，在本节仅对算法步骤加以介绍.MCMC 法中适用性最广的算法为Metropolis-Hasting（MH）算法，本文采用MH 算法进行MCMC 抽样，其步骤如下.

1）计算车道（车型）之间的转换矩阵Q：

式中：Qji为j 号车道（车型）与i 号车道（车型）的转换频率；Nji为上一车道（车型）为i，下一车道（车型）为j的频数；Ni为i 号车道（车型）的总频数.

2）根据转换矩阵Q 计算车道（车型）的平稳分布π.

3）确定上一车道（车型）i：对于初始值的确定，常采用简单概率的手段进行抽取，如以均匀分布为概率密度函数的抽样.

4）根据转换矩阵Q 进行抽样，确定下一潜在车道（车型）j.

5）构建接受域α：

6）抽取（0，1）范围内的随机数u，若u＜α，则接受转移，即下一车道（车型）为j，否则不接受转移，即下一车道（车型）为i，直至样本总数达到要求，抽样过程结束.

上述为抽取车型及车道序列的全过程，将其与传统随机车流生成方法相结合，便形成了基于MCMC 的多车道随机车流生成方法，具体抽样流程如图5 所示.

图5 MCMC 多车道随机车流抽样流程Fig.5 MCMC multi-lane random traffic sampling process

3 基于改进损伤算法及MCMC 车流模拟的疲劳寿命预测方法

3.1 应力幅谱及S-N 曲线参数

一般来说，通过有限元模拟直接获取混凝土桥梁的精确应力幅值必须基于实体单元进行模拟，然而实体单元虽然精度较高，但运算量较大，修正难度高.实际操作中可建立单元数量少，计算精度相当的梁格模型，获取桥梁关键截面的弯矩影响面，通过随机车流加载获取关键截面弯矩值，利用理论公式获得钢筋应力值，使用雨流计数[35]获取关键截面的应力幅谱.

对于S-N 曲线参数的选取，近年来，国内外学者对钢筋混凝土梁及预应力混凝土试件梁，做了大量的等幅、变幅试验，提出了多种关于钢筋混凝土梁的S-N 曲线[6，32，36]，通过比较，最终选取1.2.1 节中提出的S-N 曲线作为混凝土桥梁寿命预测的依据.

3.2 钢筋疲劳应力

《公路钢筋混凝土及预应力混凝土桥涵设计规范》中规定[37]，对于正常使用状态下混凝土桥梁中钢筋应力值可利用式（11）计算.

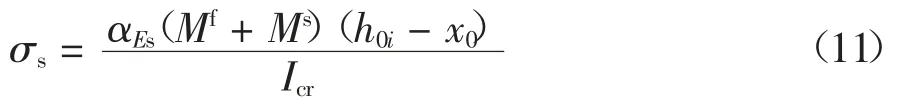
式中：σs为钢筋应力；αEs为钢筋与混凝土弹性模量之比；Mf为汽车荷载产生的弯矩值，应考虑冲击系数的影响；Ms为恒荷载下产生的弯矩值；h0i为第i 排钢筋距受压区边缘的高度；x0为受压区高度；Icr为开裂截面换算截面惯性矩.

由于应力幅值为波峰处的应力值与波谷处应力值作差而得[38]，因此恒荷载及开裂、下挠导致的初应力会对钢筋应力均值产生影响，而对钢筋应力幅并无贡献，因此本文在计算钢筋应力时仅考虑随机车流作用下产生的弯矩，即：

3.3 混凝土桥梁疲劳寿命预测流程

至此，融合改进损伤算法与MCMC 多车道随机车流模拟方法可以建立完备的混凝土桥梁疲劳寿命预测方法，实施流程如图6 所示.

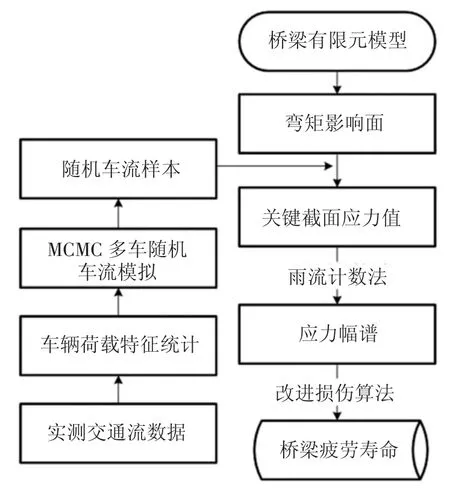
图6 混凝土桥梁疲劳寿命预测流程Fig.6 Fatigue life prediction process of concrete bridge

4 案例分析

4.1 桥梁有限元模型

采取文献[39]中的一座钢筋混凝土简支T 梁桥作为计算示例，跨径为20 m，桥梁横向布置为6.5 m（桥面净宽）+2×0.5 m（护栏），上部结构为5 片装配式混凝土T 梁，每片T 梁宽为1.5 m.主梁混凝土为C30，fck=20.1 MPa，Ec=3.0 ×104MPa；主筋采取HRB335，fsk=335 MPa，Es=2.0×105MPa，最下排钢筋距梁底40 mm.桥梁横断布置及截面尺寸如图7 所示.

图7 桥梁横向布置、截面尺寸和配筋（单位：mm）Fig.7 Bridge transverse arrangement and size and reinforcement of cross section（unit：mm）

采用有限元分析软件ANSYS 建立桥梁梁格模型，梁格模型采用Beam4 单元模拟主梁与虚拟横梁，边界约束采用简支梁桥的一般约束，即一端约束x、y、z方向的平动与x 方向的转动，另一端约束y、z 方向的平动及x 方向的转动，桥梁有限元模型如图8 所示.

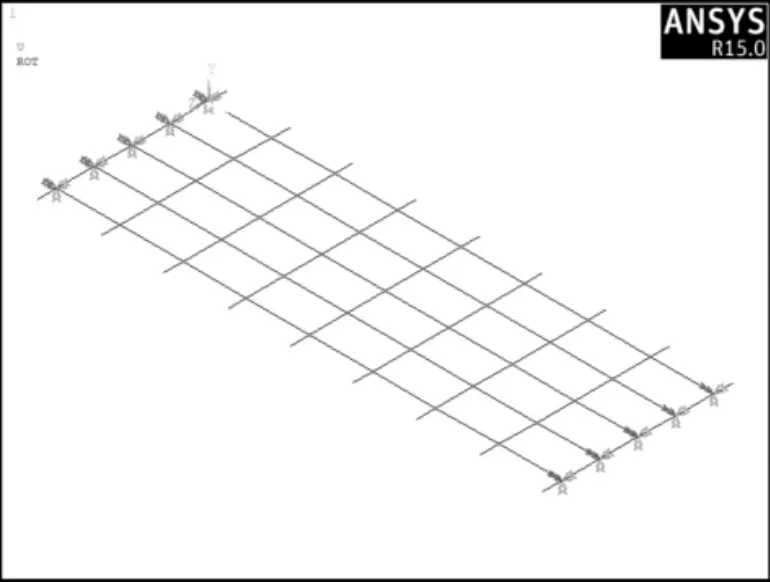
图8 桥梁有限元模型Fig.8 Finite element model of bridge

4.2 车辆荷载模型

通过河北省某高速公路1 个月内WIM 监测数据，对获取的交通流数据进行统计分析，首先对车辆荷载的时不变参数进行拟合，根据车辆的轴数、托运性质（客车、货车）及轴组类型，共筛选出11 种代表车型，详细参数见表5.

表5 代表车型参数Tab.5 Parameters of representative vehicle

分别对各种车型总重进行分布拟合，经过比较，采用核密度估计法对总重进行拟合，限于篇幅，在此仅给出占比与车质量较高的V10 车型的拟合效果图，如图9 所示.

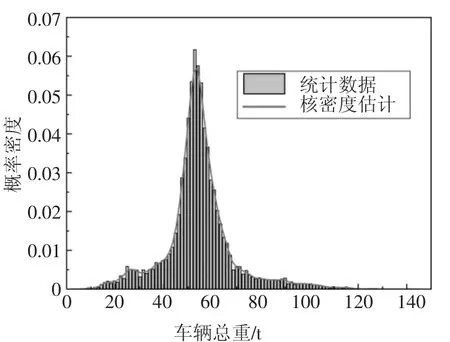
图9 V10 总重核密度拟合结果Fig.9 Kernel density fitting results of weigh of V10

从图9 可以看出，核密度估计法拟合效果良好，但其在抽样过程中往往需要求解分布反函数，相对于参数化分布抽样速度较慢，对于本案例，仅需抽取一日的交通流，抽样时间不会大量增加.

最后一项时不变信息为车辆间距，车辆间距往往无法直接获取，一般通过车速与车头时距的乘积获得，数据与广义极值Ⅲ型分布拟合较好，如图10所示，可以发现超车道的车辆间距总体大于行车道，且超过90%的车辆间距均大于20 m.

图10 车间距拟合结果Fig.10 Fitting results of vehicle spacing

根据式（9）计算车道与车型的转换矩阵，如图11所示.限于篇幅，在此仅给出占比较大的V1、V2、V3、V10、V11 五种车型之间的转换矩阵，颜色越深，表示转换概率越大.

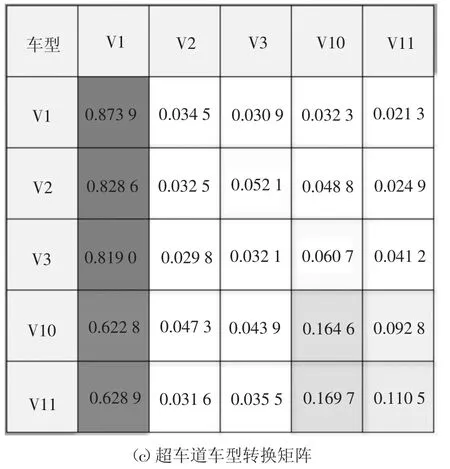
图11 车道、车型转换矩阵Fig.11 Transformation matrix of lanes and vehicle tpyes

车辆在车道内的横向位置服从正态分布，即车辆位置以车道中心线行驶为主，偶尔情况会有所偏离[40]，加之目前缺少相关实测数据支撑，因此本文随机车辆模拟中假定车辆沿各车道中心线行驶.

至此，车辆荷载的时变与时不变信息全部获取，利用MCMC 算法进行一天交通流为5 000 的样本抽样，表6、表7 分别展示了实际各车型、车道统计数据与抽样结果.从表6、表7 中可以看出MCMC 算法抽样结果与实测车流数据吻合程度较好，后续将采用所生成车流进行疲劳寿命分析计算.

表6 各车型抽样总数分布Tab.6 Distribution of total number of samples for each vehicle type

表7 各车道抽样总数分布Tab.7 Distribution of total number of samples for each lane

4.3 考虑交通量增长的加载工况

混凝土桥梁的疲劳寿命较长，在长时间的服役过程中，交通量的增长将不能被忽略，根据中国2019年度干线公路交通状况统计数据，近10 年来，公路汽车交通量波动上升，但增速有所放缓[41]，2016—2019 年，干线公路汽车交通量年均增长率（Average Annual Growth Rate，AAGR）为3.7%，分别设置AAGR 为0、1%、2%、3%四种不同年均增长率的加载工况.

4.4 改进损伤算法分析过程与结果

利用MATLAB 编制随机车流过桥的程序，通过雨流计数法得到各主梁最下排钢筋的应力幅值，并将应力幅值按从小到大的顺序平均分为100 个区间，统计得到应力幅谱.其中0～2 MPa 的应力幅值是由质量较轻的二轴车产生，对桥梁的疲劳寿命影响极小，因此计算疲劳寿命时去除这部分应力幅.图12给出了AAGR 为0 时，1 d 车辆荷载作用下1#～3#主梁最下排钢筋的应力时程与应力幅谱.

由图12 分析可知：1）应力时程曲线可分为应力密集区与应力稀疏区.应力密集区集中在0～20 MPa，主要由质量轻的2～3 轴车产生，应力稀疏区主要由重量较重的4～6 轴车产生.2）各主梁的应力幅谱的差异性较明显，且均呈现明显的多峰分布特征，这与车质量的分布特征类似.3）各主梁应力幅谱分布均存在较长的尾部，反映出该线路重载交通的影响.

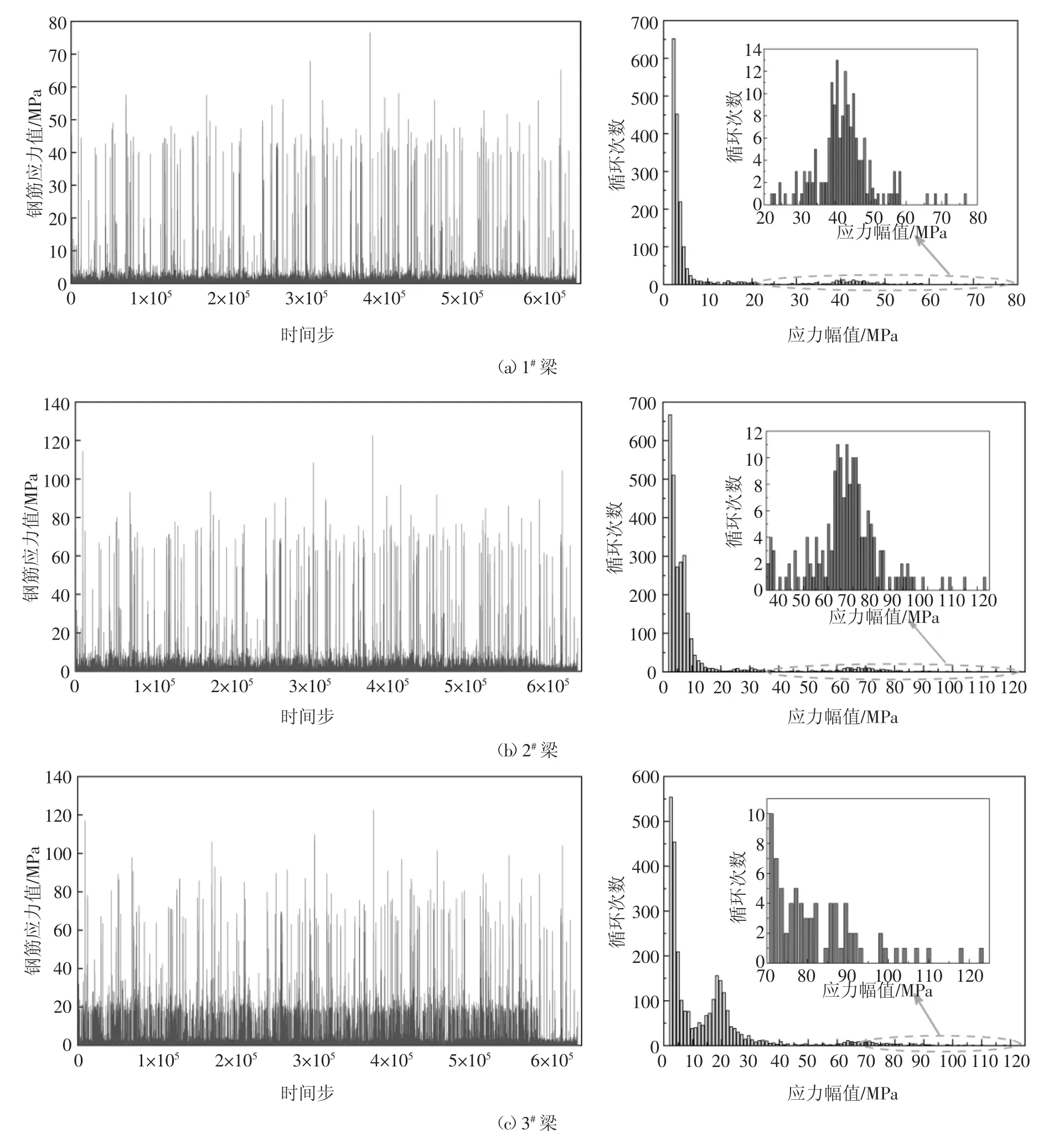
图12 1#～3#随机车流作用下主梁最下排钢筋的应力时程与应力幅谱Fig.12 Stress time-history and stress amplitude spectrum of the steel bars at the bottom of 1#～3#main beam under random vehicle

使用改进损伤算法预测程序计算各主梁的疲劳寿命，具体结果如表8 所示.从表8 可以发现：

1）4#主梁疲劳寿命最短，分析原因可能为横向加载位置的不同导致靠近车道中心线的主梁产生的应力幅值较大，加速了疲劳破坏进程，这可能与行车道重车比例高有关.

2）混凝土桥梁的疲劳寿命取决于最先疲劳破坏的主梁，AAGR 为0 时，该钢筋混凝土简支T 梁桥的疲劳寿命为77.50 年，不满足设计使用年限，造成这一结果的主要原因为大量超限车辆的存在加速了疲劳损伤的累计，因此应加强对超限车辆的管理.

3）年交通量增长对于混凝土桥梁的疲劳寿命影响较大，当AAGR 为3%时，该T 梁桥各主梁的疲劳寿命为52.49 年，较AAGR 为0 时下降32.27%，同时，其余各片梁的疲劳寿命均有大幅降低.

5 结论

1）利用一组钢筋混凝土梁与一组预应力混凝土梁变幅疲劳试验，验证了改进损伤算法的准确性，在此基础上提出公路混凝土桥梁疲劳寿命预测流程，可为混凝土桥梁疲劳寿命预测提供参考.

2）基于河北省某高速公路的实测交通数据生成多车道随机车流样本，以一座跨径为20 m 的钢筋混凝土简支T 梁桥为例进行分析，确定了日均交通量为5 000 时的桥梁疲劳寿命.结果表明：利用改进损伤算法预测，AAGR 为0 时，该混凝土桥梁的疲劳寿命为77.50 年.年交通量增长对于混凝土桥梁的疲劳寿命影响较大，当AAGR 为3%时，该T 梁桥疲劳寿命较AAGR 为0 时下降32.27%.

3）本文所采取的车辆荷载模型具有明显的地域特征，对其他地区的桥梁疲劳寿命预测不能一概而论，应该采取真实的交通流模型.此外，在进行预测时未考虑外部环境、钢筋腐蚀等带来的影响，后续研究工作中将综合考虑相关因素对混凝土桥梁疲劳寿命的影响.

4）采用了5 组带筋混凝土梁试件对所提出的改进损伤算法进行了验证，但由于构件数量的限制，相关结果仍需进一步研究与论证，后续研究工作将进一步对其进行完善.