基于分层四叉树的多分辨率数字岩心的表示与生成*
陈国军 裴利强 李 胜 姜 朕
(中国石油大学(华东)计算机科学与技术学院 青岛 266580)
1 引言
数字岩心技术是通过特定技术对岩心进行模拟,建立岩石三维数字化图像,根据数字岩心技术生成的数字岩心模型能够反映真实岩心微观孔隙结构,模拟岩石物理属性及实验,可以精确地分析岩心各项特征和性质。相比于传统的岩石物理实验,数字岩心技术快速简便,省时省力且结果精细等优点。
数字岩心的建模方法[1~5]根据建模数据的来源可以分为两种:物理重建与数值重建,物理重建全部使用外部数据重建数字岩心,不通过计算机模拟岩心的结构元素;数值重建则部分依靠外部数据,然后通过计算机模拟出数字岩心。物理重建分为X射线扫描成像法和切片组合法等[6~8]。
X射线CT技术出现和发展[9],促进了数字岩心技术的发展,通过CT设备扫描,能够获得分辨率极高的岩心二维图像,使得建立精细、准确的数字岩心孔隙骨架结构更加简单便易。
数字岩心的表现形式有多种,体素模型、面模型、孔隙网络模型[10]等,其中体素模型是对真实数字岩心进行数据建模的一种直观表示方式,用一系列规则尺寸的体元(如立方体和正十二面体等)来模拟岩心空间。建立体素模型数字岩心的一般步骤:首先将二维岩心切片预处理,分割岩心骨架和孔隙像素,叠加到三维场景中,根据每一层切片像素信息生成对应的体素。体素模型模拟数字岩心的特点是简单、准确,便于进行岩心孔隙骨架空间分布的研究。但体素数字岩心容易带来数据冗余、占用存储空间大等问题,难以在普通计算机上进行快速生成和渲染,因此,需要采用和合理的数据组织方式。通常,数字岩心部分结构需要较高分辨率与精度,以获得更多的细节信息,而其余部分则不需高分辨率,难以平衡分辨率问题。张晴等[11]分别对页岩岩心采用高、低两个分辨率获取二维切片图像,然后分别建立了二者的数字岩心,在低分辨率下建立的页岩数字岩心,为了表征出内部的纳米级孔隙特征,选取特定的区域,在高分辨率下建立了相应的数字岩心。崔利凯等[12]利用图像配准方法将不同分辨率下的岩心扫描图像进行空间配准,按照分辨率从高到低的顺序进行孔隙及骨架分割,构建多尺度、多组分的数字岩心模型。有些研究[13~18]采用八叉树的方式组织数据,但八叉树仍存在构建较为耗时,遍历复杂,维护管理不方便等问题,且在X、Y、Z三个方向上分辨率相同,在表示模型边界时精确度不高,三个方向上尺寸相差较大的情况下造成了数据的冗余。刘亚静[19]等对八叉树数据结构进行扩展,将形体的边界信息单独存储,然后对三维矿体进行重构,提升了模型的边界精度。
本文针对传统的数字岩心建模方法造成的数据量过大,耗时过长,难以表示多分辨率等问题,提出了分层四叉树模型,在此模型基础上建立多分辨率数字岩心体素模型,同时结合MC算法[20],生成数字岩心面模型。最后通过实验给出了分层四叉树与普通方式以及八叉树在性能上的对比。
2 CT切片预处理
通过射线扫描获得的CT切片为灰度图,像素灰度值分布为0~255,需要设置阈值,将孔隙和骨架进行分割,以分别获得骨架和孔隙数据。阈值分割方法实际上通过对比阈值将阈值两边的像素点灰度值二值化,设分割阈值为T,像素点(i,j)的灰度值为f(i,j),若f(i,j)>T,则令其灰度值为255,否则为0,计算式如式(1)所示。
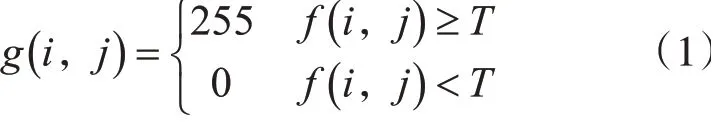
阈值分割算法的关键是确定阈值,如果能确定一个合适的阈值就可准确地将图像分割开来。阈值分割法主要分为全局和局部两种,目前应用的闭值分割方法都是在此基础上发展起来的,比如最小误差法、最大相关法、最大嫡法、矩量保持法、最大类间方差法等,而应用最广泛的是最大类间方差法。
本文采用最大类间方差法进行计算阈值,再结合孔隙度,进行阈值修正,最后根据阈值区分骨架和孔隙像素数据。
1)最大类间方差
最大类间方差法OTSU[21~23]是一种自适应阈值确定的方法,基于全局的二值化算法,它是根据图像的灰度特性,将图像分为前景和背景两个部分。当取最佳阈值时,两部分之间的差别应该是最大的,在算法中所采用的衡量差别的标准就是较为常见的最大类间方差。
记T为前景与背景的分割阈值,前景点数占图像比例为w0,平均灰度为u0;背景点数占图像比例为w1,平均灰度为u1,图像的总平均灰度为u,前景和背景图像的方差,计算如式(2)所示。
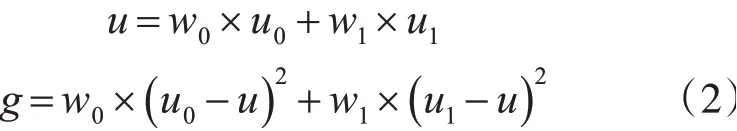
当方差g最大时,可以认为此时前景和背景差异最大,此时的灰度T是最佳阈值。
2)阈值修正
采用最大类间方差法计算得到的阈值,只是从概率角度计算得到的,用这个阈值进行分割像素,导致孔隙像素个数较多,得到的孔隙度过大,为此需要进行修正。
根据岩心的孔隙度φ和最大类间方差法计算得到的阈值为T0及岩心总的像素个数C。分别计算T=T0±di时的孔隙像素个数Ci/C和Ci/C,最终阈值取|φ-Ci/C|最小时的T作为阈值,如式(3)和(4)所示。
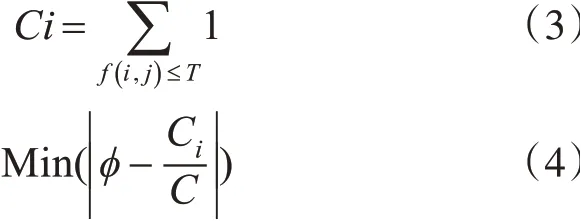
3 分层四叉树模型
四叉树和八叉树[24]是分别用来描述二维空间和三维空间的树状数据结构,八叉树每个节点下至多可以有八个节点,通常把三维空间划分为八个区域,区域的信息存储在每个节点中,若细分区域中没有信息或具有一样的性质,则节点不再细分。四叉树则用来表示二维空间。
本文提出分层四叉树模型,根据本文实际情况将四叉树扩展到三维空间,采用多层四叉树的方式组织CT切片数据,分层四叉树结构如图1所示。
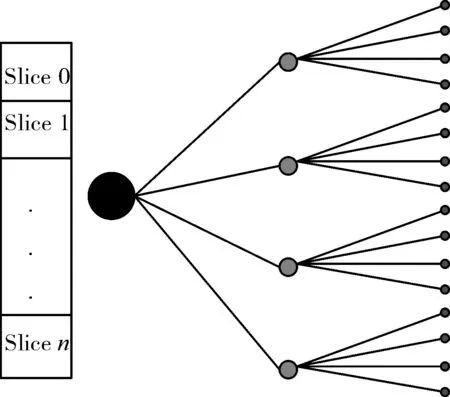
图1 分层四叉树示意图
3.1 分层四叉树模型定义
每层CT切片生成一棵四叉树,由一个一维数组存储每棵树的根节点。四叉树节点数据结构包含节点类型、节点坐标位置、节点的子节点指针等。
四叉树任一节点的子节点为四个或零个,若节点范围内存在像素值不同的像素点,即不满足式(15),则节点细分为四个子节点,子节点每个维度上 的 边 长 分 别 为L1=(xmax-xmin)/2、L2=(ymaxymin)/2,若范围内像素值一致,即满足式(5),则节点为叶节点,节点中存储范围坐标、子节点指针及节点像素属性等信息,对于四叉树,所有叶节点满足节点内像素属性一致。
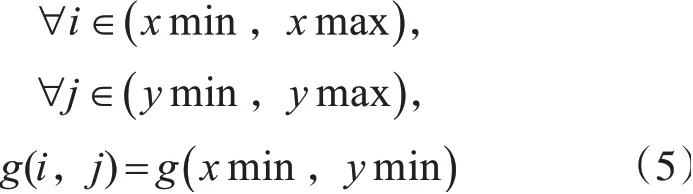
单层CT切片生成的四叉树如图2所示。
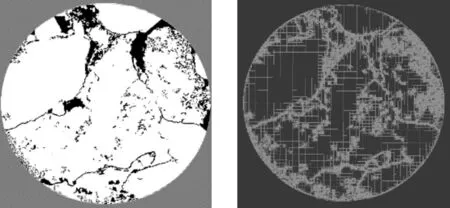
图2 单层CT切片四叉树示意图
3.2 分层四叉树模型扩展
分层四叉树由于结构特点,其管理较为快速简便。遍历:通过根节点数组直接获得根节点指针,然后通过节点存储的子节点指针进行遍历,直至满足条件,对于树T,其深度depth(T)=max{log2rmax,log2cmax};拆分:将待拆分节点根据节点范围坐标一分为四,得到新的四个叶节点,对新的叶节点进行赋值;合并:由于四叉树节点子节点数要么为0要么为4,因此合并即为4个子节点合并,直接将4个子节点删除,保留其父节点即可。
4 数字岩心的多分辨率模型生成
4.1 多分辨率扩展
首先由低分辨率CT切片数据建立四叉树模型。
通过高分辨率模板对低分辨率CT切片进行修改时,低分辨率CT切片孔隙、骨架像素点可能会发生翻转变化,因此需要对四叉树进行相应的修改扩展。设扩展切片号为n,模板所在行列值范围为rmin~rmax,cmin~cmax。
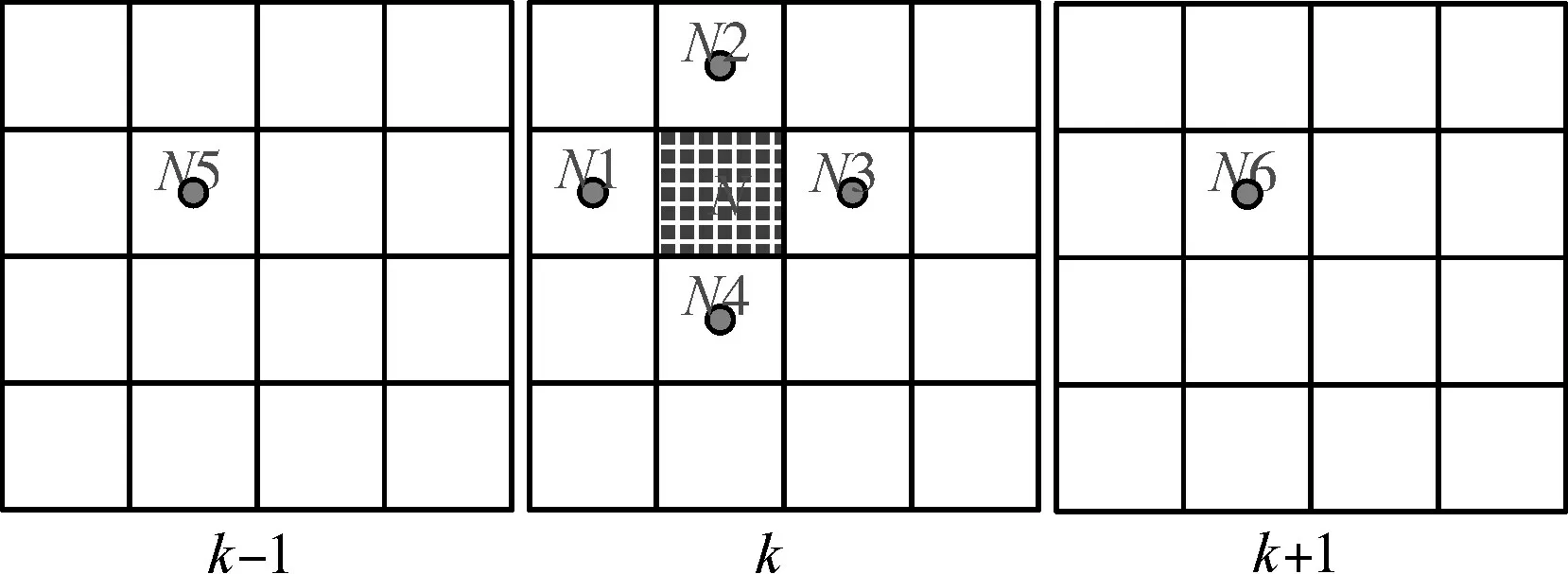
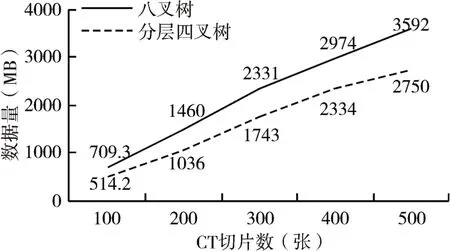
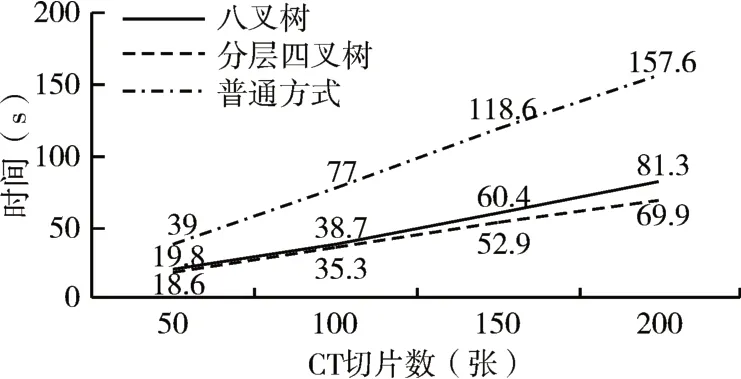
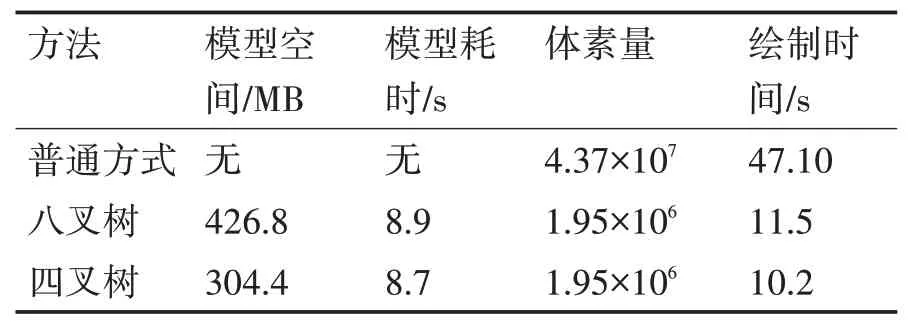
根据切片编号i从根节点数组中取出对应四叉树根节点RootNode=Slice(n);从根节点通过子节点指针进行遍历,比较子节点Si坐标范围与模板所在行列范围,若满足rmin>xmin,rmax 图3 模板割分示意图 依据根节点数组,遍历每一层切片(即每一棵四叉树),根据节点属性由式(6)判断节点类型,取出叶节点中存储的坐标信息,由xmin、xmax、ymin、ymax、z、z+1构建立方体体元,同时根据节点属性分别赋予骨架体元和孔隙体元不同渲染颜色。 等值面的梯度分量在沿面的切线方向为零,所以,该点的梯度矢量的方向就代表了该点的法向方向[15]。为了方便后续等值面法线的计算,体元各顶点法向量通过差分公式计算: 式中:Δx、Δy、Δz分别代表体元三个方向上的间距,此处Δx=Δy=Δz=1,gx、gy、gz分别代表坐标点(i,j,k)三个方向上的梯度值,法向量为N。 4.3.1 基于分层四叉树的MC算法 Marching Cubes算法是一种经典的等值面提取算法,它的原理是在由一系列二维图像组成的三维图像库中选取上下连续两层相邻8个像素点作为定点组成的立方体体元中,根据8个顶点的像素值生成三角形截面,即等值面。对体元中8个角点的像素值进行判断,如果顶点值为0,则说明该顶点为孔隙点,将该点标记为0,如果顶点值为255,则说明该点为骨架点,标记为1,遍历体元8个顶点,便得到孔隙、骨架点的分布情况,如果体元一条边的两个顶点属性不一样,那么截面一定经过此边,由此规律,可以找到体元中与截面三角形相交的边,进而分析出体元中截面的分布情况。体元顶点标记只有0和1两种情况,所以总共存在28=256种不同的体元。由旋转和对称变换可知256种体元可以总结为15种。 由分层四叉树模型构建体元:依据CT切片行列值坐标i∈(rmin,rmax)、j∈(cmin,cmax),依次构建体元的八个顶点,对于体元顶点p(i,j,k),对分层四叉树k进行遍历,得到叶节点N,若满足xmin 使用高分辨率模板对分层四叉树模型进行扩展后,造成局部节点细分,分辨率变高,体元的构建亦须相应的改变。如图4所示,节点N为扩展节点,将其进行标记,视为高分辨率节点,构建体元时须提高分辨率,然后遍历其邻接节点N1、N2、N3、N4、N5、N6,判断节点N与邻接节点交界处像素值是否一致,若与邻接节点Ni像素不一致,则节点N与Ni间有等值面产生,构建体元时须细分邻接节点节点Ni,提高分辨率,将Ni进行标记,同时对Ni与其邻接节点执行上述操作;若与邻接节点Ni像素一致,则停止标记。至此,N节点及其周围被标记节点即为构建体元时须细分节点。 图4 局部扩展示意图 标记完成后,进行体元构建时,若p(i,j,k)位于被标记节点起始位置,即高分辨率节点,则此节点在构建体元时须细分,此时以模板分辨率为体元边长进行体元顶点的搜索构建体元,查找等值面,至节点结束位置。 4.3.2 截面顶点坐标及法线计算 本文体元顶点只有孔隙和骨架两种属性,为了计算方便,截面顶点直接取所在边中点,同时法线即所在边顶点法线均值,如式(11)所示,其中N(i1,j1,k1),N(i2,j2,k2)分别为截面顶点所在边两端顶点法向量。 为了检验算法效果及时间、存储上的性能,本文的实验在Windows10平台进行,机器配置为E5-1620CPU,16G内存,NVIDIA Quadro K2000图形显卡,开发工具有VS2015,OpenCV开发库,OpenGL图形库,使用的数据为吉林某油藏储层岩心CT扫描切片,图像分辨率为995×968,数量为60张。采用本文方生成的数字岩心效果如图5、图6所示。 图5 数字岩心模型 图6 局部多分辨率扩展前后对比图 除了采用上述提出算法进行实例建模,实验还采用普通方法以及传统的八叉树对相同数据进行建模实验,与本文方法性能对比如表1、图7、图8所示。 图7 不同模型内存占用对比 图8 体素数字岩心总生成时间对比 表1 不同方法性能对比 结果表明,与普通方式相比,采用八叉树以及分层四叉树,生成多尺度模型,能够使体素量减少95%以上。与八叉树相比,本文的分层四叉树模型存储空间占用减少30%左右,同时缩短了数字岩心模型重建耗时。 实验证明,本文采用的方法建立的多分辨率数字岩心模型能够精确地模拟显示真实岩心的空间特征,同时优化了传统建模方法存在的数据冗余,存储空间消耗大,建模耗时等缺点。多尺度数字岩心模型通过分层四叉树组织,利于后续模型的维护及扩展等操作。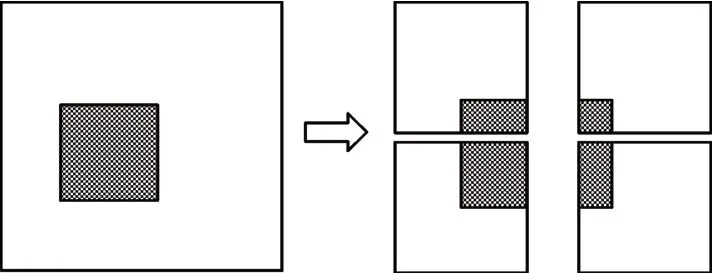
4.2 体素数字岩心

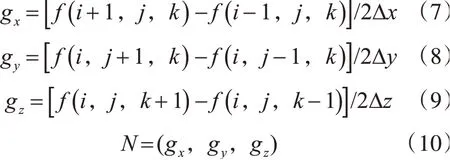
4.3 面数字岩心
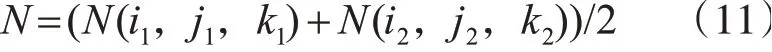
5 实验结果分析


6 结语

