基于改进的K-means入侵检测算法*

季赛花 黄树成

（江苏科技大学计算机学院 镇江 212003）

1 引言

随着互联网的飞速发展与快速普及，网络已经成为人们在生活中不可缺少的部分。互联网固有的开放性与共享性在给人们带来便利的同时，伴随而来的是现今人们极为关注的相关网络信息安全问题［1］。基于信息加密技术、防火墙等静态安全防御技术已经无法适应动态变化的网络，入侵检测作为一种积极主动的安全防护技术，弥补了静态安全技术的缺陷［2］，提供了对内部攻击、外部攻击和误操作的实时保护。

数据挖掘技术能从海量数据中挖掘出有用的知识，进而应用于入侵检测中，识别正常或异常行为，能有效提高入侵检测效率。而聚类分析是数据挖掘重要的一部分。它能通过分析数据的属性特征，将特征相近或相似的数据划分到同一个类中。K-means算法是一种典型的聚类算法，具有快速简单，具有较高的大数据集运算效率［3］。将K-means算法运用于入侵检测中，在数据处理和分析方面有明显的优势，但是K-means算法也有一些缺点，比如聚类数目需要事先给定，聚类结果对初始中心点和数据集中的噪声点以及孤立点敏感，且聚类结果易陷入局部最优［4］。近年来，很多学者对传统的K-means算法进行改进，并将其应用于入侵检测中。徐超［5］等在基于最大最小距离算法的思想和有效性指标基础上，迭代计算出最优聚类数和其对应的聚类中心，并用于构建正常行为模式库，入侵检测性能有所改善。李鹏［6］等将K-means与决策树结合，根据信息增益比差异将样本数据先分类再建立决策树，提升了算法的检测率，但对未知攻击的检测能力较低，因此，传统K-means算法在入侵检测应用上仍存在不足。

为此，文中提出了一种改进的K-means算法，基于类内和类间的聚类有效性指标的确定聚类数目，在聚类过程中对距离进行特征加权，并结合三支决策聚类思想，扩展了K-means算法使之适用于不确定性聚类，进而提高入侵检测的检测率，降低误检率。

2 传统K-means聚类算法

2.1 算法过程

K-means算法是1967年由J.B.MacQueen首先提出的一种无监督聚类算法［7］。其算法思想比较简单，即在无类标签的数据集中，将N个对象划分到K个簇中，使得相似度较高的在一个类中，差异较大的在不同的类中，其算法流程［8］如下：

1）从给定的数据集中选择K个点作为初始聚类中心点；

2）对每个样本点，计算样本点到各个聚类中心点的距离，选出最小距离对应的聚类中心点，并将其划分到该聚类中心点对应的聚类中；

3）计算每个聚类中所有点的均值，将此均值点作为新的聚类中心；

4）循环2）、3），直到每个聚类的中心点不再发生变化，目标函数收敛，算法结束。

其中，一般采用欧式距离去计算样本点到各个聚类中心点的距离，见式（1）；采用均方差作为目标函数，见式（2）。

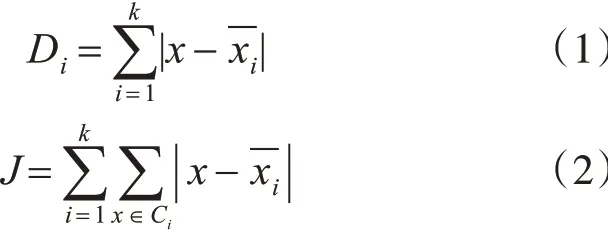
2.2 算法在入侵检测应用中的不足

K-means算法操作简单、运算速度快，将其应用于入侵检测中具有重要的研究价值。但同时也存在一些不足之处。其中，聚类的数目难以估计，不确定的K值会导致聚类质量下降［9］。入侵检测中从网络中抓取的数据包都是实时的，所以难以确定聚类数，致使聚类效果不稳定，从而影响入侵检测的性能［10］。

3 算法的改进

3.1 特征加权

网络数据呈现多维性，而每条数据的每个特征对聚类的作用都不尽相同，所以需要对不同特征进行权值分配［11］。本文兼顾类内和类间对象的关系，利用前次迭代中产生的均值、方差等确定权重。

设数据集X中有N个D维数据为第k类的第d维上的均值为当前第k类的方差在第d维上的取值，如式（3）所示。

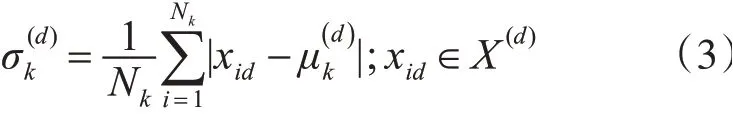
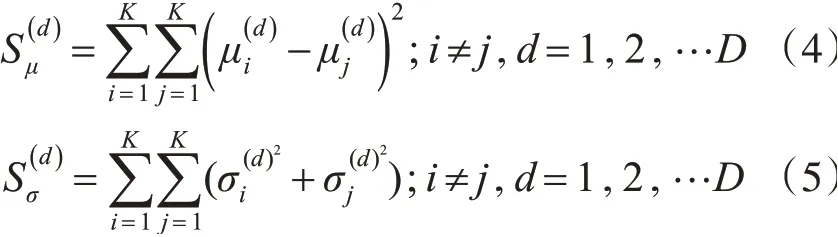
整个数据集X在第d维特征上所有的聚类均值总和（式（4））与方差总和（式（5））为表示第d维特征在各类别中心的间距表示第d维特征的类内离散度大小。为了达到理想的聚类效果，类间距离越大越好，类内离散度越小越好。所以，可以设一个第d维特征类间距离与类内离散度的比值作为第d维特征的聚类效果的指标，如式（6）所示。

那么第d维特征在聚类过程中的权重，即为第d维特征的聚类效果指标与各维特征聚类效果指标之和的比值。如式（7）所示。

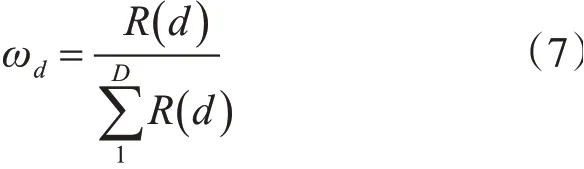
即求得各维特征的权重。继而得到数据集中任意xi至聚类中心uj的距离特征加权公式，如式（8）所示。

3.2 K值有效性指标

本文算法K值有效性指标利用上述的特征加权距离综合考虑类内紧密性与类间分离性。

设在数据集U中，Ci表示其中被划分的一个类，定义类内距离Intra（Ci）为类Ci中任意两个数据x，y的距离平方和，如式（9）所示；定义类间距离Inter（Ci，Cj）为类Ci到其他类Cj的距离，如式（10）所示。其中，k、p分别是类Ci和类Cj中数据样本点的个数。

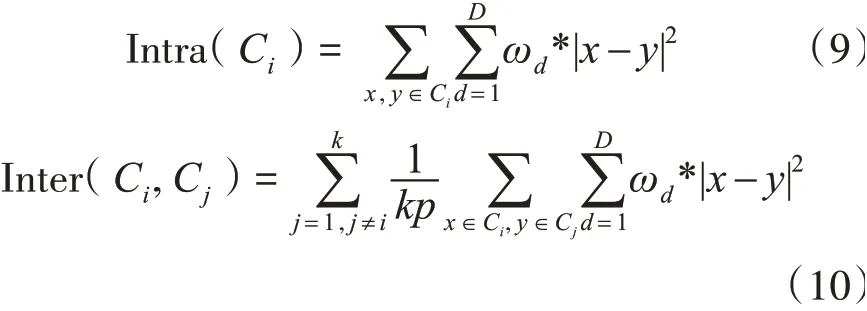
3.3 三支决策聚类

三支决策（Three-way Decisions）最早由Yao［12］在粗糙集理论的基础上提出的。在人们实际决策中，由于对事件信息了解程度不同，往往会做出三种类型的决策：接受、拒绝和延迟。对于那些有充分把握的事件，人们很容易做出接受或拒绝的决策，但是对不确定事件，人们往往不能立马做出决策，需要延迟决策［13］。该理论与传统的二支决策相比，更有实际意义。基于此，将三支决策引入到聚类分析中，考察对象与类之间的关系，可划分为对象属于这个类，对象不属于这个类以及对象可能属于这个类。

结合三支决策思想，在一个数据集U中，针对一个类C，与其有关联的有三个互不相交的区域：CI、CB和CO，又称I域，B域和O域［14］。I域中的对象确定属于这个类，O域中的对象确定不属于这个类，B域中的对象可能属于也可能不属于这个类，即类C的构成为C={CI，CB}。为保证有实际的意义，需 满 足1）

3.4 改进的K-means算法

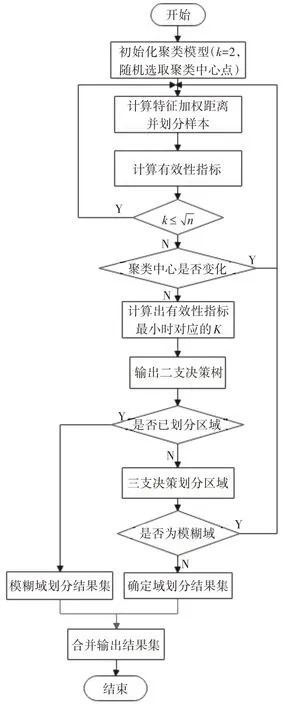
图1 改进的算法流程图

具体的步骤如下：

输入：数据集X=｛x1，x2，…，xn｝，初始聚类数目k=2。

输出：聚类结果C。

1）在数据集中，随机选取k个初始聚类中心点U=｛u1，u2，…，uk｝；

2）计算数据集中除了聚类中心点外剩余数据对象xi到每个聚类中心uj的特征加权距离dist(xi，uj)，并把他们划分到距离最近的簇Cj中；

4）如果聚类中心不发生变化，转至5），否则转至2）；

5）计算k=arg［S］，如果，那么，转至1），否则转至6）；

6）k'=argmin［S］，最终输出新的二支聚类结果集C'；

7）遍历C'，对于每一个类若则若，且，则，否则

4 仿真实验及分析

4.1 实验环境及数据说明

本文实验借助的硬件平台是Intel（R）Core（TM）i5-3230 CPU@2.60Hz，4GBRAM的计算机，并在Win7系统上采用在Python编译器上实现程序设计。

本实验使用KDD Cup99数据集中的corrected.data作为训练集，使用10%的数据样本作为测试集。KDD Cup99数据集中的每条数据由41个特征属性和1个决策标签组成［16］。其中决策标签分为正常（Normal）和攻击类型，攻击类型有四大类：DOS，R2L，U2R，Probe。数据格式如下例所示：2，tcp，smtp，SF，1684，363，0，0，0，0，0，1，0，0，0，0，0，0，0，0，0，0，1，1，0.00，0.00，0.00，0.00，1.00，0.00，0.00，104，66，0.63，0.03，0.01，0.00，0.00，0.00，0.00，0.00，normal。

由于数据集中含有符号型数据属性，不适合聚类测试，同时也为了避免“大数吃小数”现象，故对先要对数据进行数值化和归一化处理。

4.2 结果分析

本改进模型的实验结果评估指标主要有两项：检测率（Detection Rate，DR）和误报率（False Posi⁃tive Rate，FPR）。

检测率DR的公式如式（12）所示：

误报率FPR的公式见式（13）：

由上述公式可以看出，误报率越小，检测率越大，入侵检测性能越好。

改进前后的算法应用到入侵检测中所得到的检测率和误报率见表1。

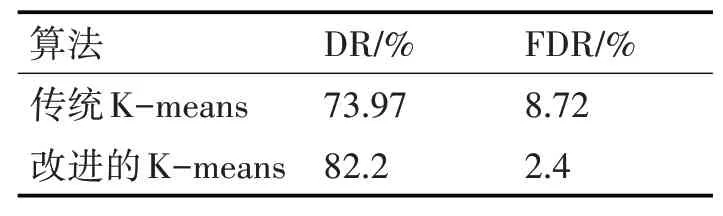
表1 实验测试结果对比

如图2所示，以误报率为横坐标，以检测率为纵坐标画出改进前后的入侵检测算法的ROC曲线对比图，由此可以很直观地看出本文的入侵检测算法的面积大于未改进的K-means算法的面积，可以说明本文的入侵检测算法性能更好，检测效率更佳。

图2 ROC曲线

5 结语

针对传统的K-means算法无法准确确定聚类数目而导致聚类质量下降的问题，本文提出了基于改进的K-means入侵检测算法，一方面考虑数据的各维特征属性对聚类作用不一，提出对聚类过程中所涉及的数据点到聚类中心点的距离进行特征加权；另一方面，基于类内和类间的聚类效果有效性指标来确定聚类数目；最后结合三支决策聚类思想，划分确定域和模糊域，对模糊域中的数据延迟决策，进而提高了聚类的检测率，降低了误报率。