Atangana-Baleanu分数阶双稳系统的随机共振现象

汪洋百慧， 郑永军， 罗 哉

(中国计量大学 计量测试工程学院，浙江 杭州 310018)

1 引 言

在微弱信号检测中，有用信号总淹没于强噪声中，这阻止了有用信号的提取，因此人们总想滤除噪声[1,2]。但经过大量研究表明噪声在某些条件下反而可以产生积极有利的作用[3～5]。其中随机共振在微弱周期信号、噪声和非线性系统的协同作用下增强输出信号的幅值，以此达到微弱信号检测的目的[6,7]。目前为止，大部分研究人员仍将重点放在整数阶模型上。若系统更加复杂，仍使用传统的整数阶模型将会存在很大的局限性，而分数阶模型能很好地解决以上问题[8～10]。

随机共振通常发生在布朗粒子反常扩散过程中，具有非马尔可夫特性。由于分数阶微积分特点是在时间上的记忆性和空间上的关联性[11～19]，因此可用来描述这类现象，并且基于分数阶系统的信噪比等衡量指标更优异。最常用的分数阶微积分定义是Grünwald-Letnikov(G-L)定义，Riemann-Liouville(R-L)定义和Caputo定义。然而有学者指出上述分数阶微积分的内核是非局部的，但具有奇异性[20]。Atangana和Baleanu在2016年给出了一种新形式的分数阶微积分，有效解决了这一问题[21]。其中借助广义Mittag-Leffler(M-L)函数作为非局部和非奇异核，使其具有均方位移的交叉性质并保证了信息在延展的开始和结束时的一致性[22～24]。

本文根据Atangana和Baleanu新提出的分数阶微积分，构建了双稳系统的分数阶Langevin方程，该系统解决了奇异性问题，能够更好地描述随机共振的动力学特性。同时基于该方程，在Simulink环境下对其进行仿真实验，采用控制单一变量法，分别在有无噪声时调节分数阶求导阶次、固定分数阶求导阶次不变调节噪声强度大小这3种情况下，分析随机共振的动态特性。

2 Atangana-Baleanu分数阶微积分

2.1 Atangana-Baleanu(简称A-B)分数阶微积分的定义和性质

当f∈H1(c,b)，b>c，α∈[0,1]时，基于Caputo的A-B分数阶导数的定义如式(1)所示：

(1)

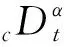
M(α)的定义如式(2)所示[25]：

(2)

式(1)中Eα是在整个复平面上由以下幂级数定义的一个Mittag-Leffler(M-L)函数，其定义如式(3)所示：

(3)

当α=1时，式(3)可以写为式(4)所示：

(4)

基于Caputo的A-B分数阶导数更加严谨。但当α=0时，原函数不存在。为了避免这个问题，提出了以下的定义。

当f∈H1(c,b)，b>c，α∈[0,1]时，基于R-L的A-B分数阶导数的定义如式(5)所示：

(5)

上述定义将有助于讨论现实世界中的问题，并且在使用拉普拉斯变换解决初始条件下的某些物理问题时也将具有很大优势。经过简单计算后得到基于Caputo的A-B分数阶导数的Laplace变换如式(6)所示：

(6)

基于R-L的A-B分数阶导数的Laplace变换如式(7)所示：

(7)

基于上述定义，分数阶控制系统可以由式(8)表示：

(8)

式(8)可以写为式(9)所示的传递函数的形式：

(9)

2.2 分数阶导数的逼近算法

在实际应用或仿真实验中需要对分数阶传递函数进行求解，由于其形式比较复杂，直接求解较为困难。本文对传统的Oustaloup算法进行改进，用其无限逼近于分数阶传递函数，这对于后续求解分数阶控制系统有着较好的提升作用。

改进后的Oustaloup算法基于如式(10)所示的传递函数：

H(s)=sα

(10)

在给定的频段[ωb,ωh]内，式(10)可以写为式(11)所示[26]：

(11)

式中： 0<α<1，s=jω，b>0，d>0。

在频率ωb<ω<ωh范围内，利用泰勒公式对式(11)展开得到如式(12)所示：

(12)

式中：p(s)的表达式如式(13)所示：

(13)

忽略式(13)中二阶及其无穷小量，sα可以写为式(14)所示：

(14)

式中：无理小数部分可以用连续时间有理模型近似表示为式(15)所示：

(15)

根据实零点和极点的递归分布，第k个零点和极点可以写为式(16)所示：

(16)

综上，sα的整数阶近似公式为式(17)所示：

(17)

式中：K为系统增益，如式(18)所示：

(18)

经过大量实验验证，一般取b=10，d=9。

3 分数阶双稳态随机共振系统

3.1 随机共振的基本原理

图1是一个未加外力的双稳系统在过阻尼情况下的势函数，表达式如式(19)所示：

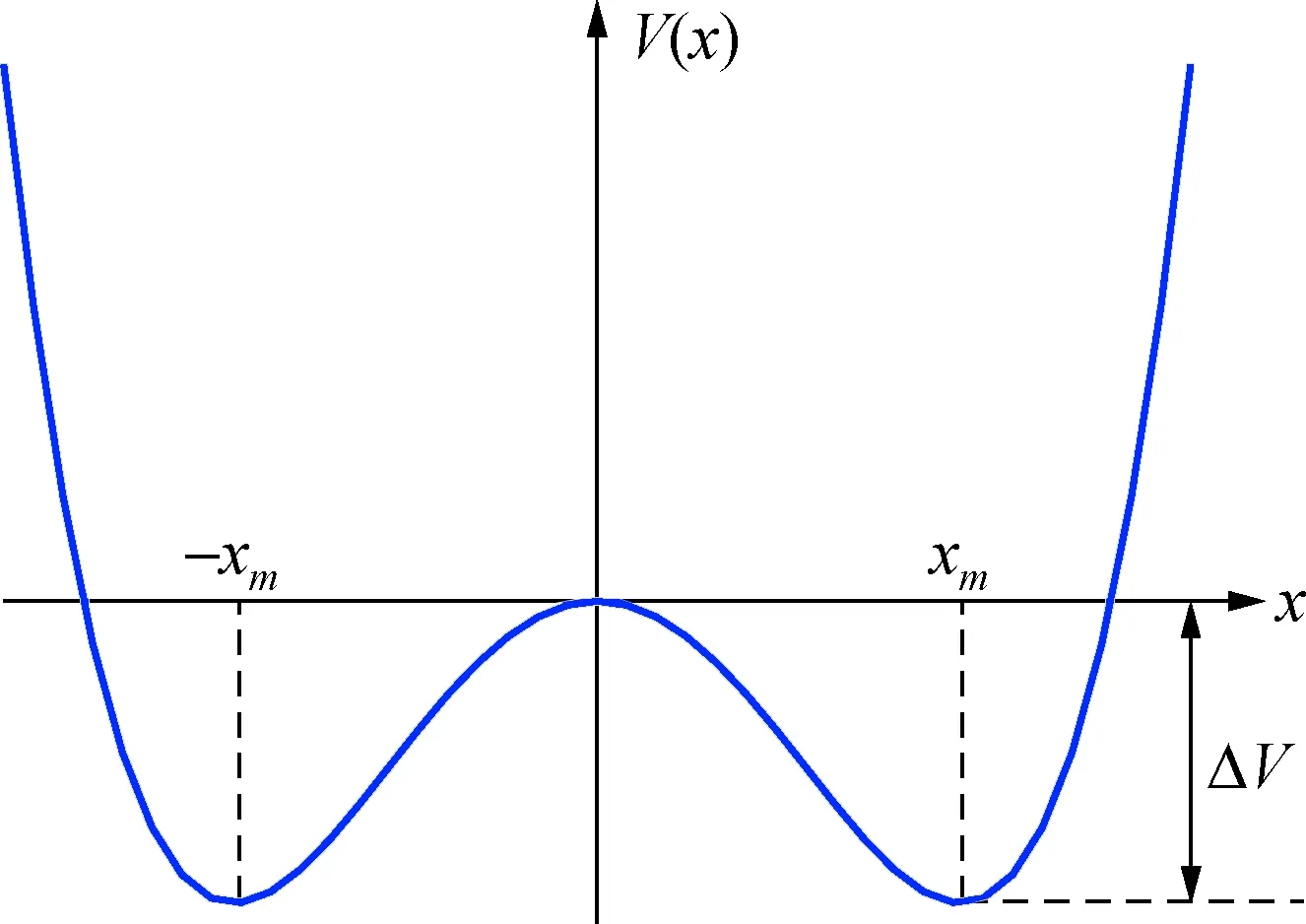
图1 双稳系统的势函数Fig.1 Potential function of bistable system

(19)

式中：a>0；b>0；x为系统输入；V(x)为系统输出；势阱点为±xm=±(a/b)1/2；势垒点x=0；势垒高度为ΔV=a2/4b。

由图2(a)所示，在未受外力的作用下，双稳系统的两个势阱相同且关于纵坐标对称。

将噪声加至系统后，布朗粒子会在两势阱之间来回跃迁，其跃迁速度可用克莱莫斯(Kramers)速率表示，如式(20)所示[27]：

(20)

式中：D为噪声强度；ΔV为势垒高度。

如图2(a)到2(b)的变化可以看出，若系统存在微弱周期信号作用时，其势阱不再对称。此时势垒高度改变了，从而Kramers速率也发生了变化。当Kramers速率为外加力频率2倍时，系统能够产生随机共振现象[28]。再将微弱信号加至系统，势函数将会如图2所示的变化规律不断转变。

图2 随机共振现象原理图Fig.2 Schematic diagram of stochastic resonance phenomenon

上述双稳态系统的随机共振现象，其动力学特性可以用Langevin函数表示，如式(21)所示[29]:

(21)

式中：A0cos(ωt+φ)为周期性调制信号；ξ(t)为噪声信号，通常为白噪声信号。

3.2 分数阶Langevin方程

大量研究表明，在相似条件下，基于分数阶微分方程的随机共振系统具有更加丰富的动力学现象[30～34]，所以本小节将整数阶Langevin方程推广至分数阶下。

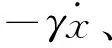
(22)

(23)

在粘性介质中，布朗粒子的运动是一个非马尔可夫过程，在时间和空间上都具有相关性。为了解决这个问题，提出了广义的Langevin方程来描述布朗粒子的反常扩散，如式(24)所示：

(24)

由于阻尼力和噪声都源于布朗粒子与周围介质分子之间的随机碰撞，因此随机力ξ(t)和阻尼核函数γ(t)满足以下涨落耗散定理:

〈ξ(t)〉=0,〈ξ(t)ξ(t′)〉=kBTγ(t-t′)

(25)

式中: kB为玻尔兹曼常数；阻尼核函数可以写为：

(26)

将式(26)代入式(24)中：

(27)

又因为式(1)成立的条件是建立在t→τ的时候，即当(t-τ)α→0时M-L函数有：

(28)

所以，式(1)可以写为：

(29)

由此能够得到过阻尼情况下的分数阶Langevin方程为：

(30)

4 仿真验证及分析

本章将基于分数阶Langevin方程，采用单一变量的方法，研究各个参数变化对基于新分数阶导数的双稳态系统随机共振现象的影响。这里微弱周期信号取F(t)=Acos(2 π ft)，设系统参数a=b=1，代入(30)中可得：

(31)

4.1 未加噪声时改变分数阶求导阶次

当微弱周期信号的幅值A=0.3，频率为f=0.01 Hz时，无高斯白噪声输入的情况下，只改变分数阶求导阶次。

如图3(a)所示为基于A-B分数阶导数时，分数阶求导阶次以0.1的步长从0.1递增到0.9的输出响应的时域图。可以看出α的变化改变了势垒高度的大小并使势阱点发生漂移。当α大于0.6时，布朗粒子只能在x=1或x=-1的单一势阱处运动，说明其没能越过势垒。减小α，当α小于0.6时，可以看出布朗粒子的运动轨迹发生了改变，在x=1和x=-1之间运动。说明α值越小，系统的内核函数在时间上的记忆性越强，布朗粒子就有足够大的能量可以越过势垒。

图3 A=0.3时α变化下系统输出时域图Fig.3 Time-domain diagram of system output under the change of α when A=0.3

如图3(b)所示，做了进一步分析得到了该系统更加精确的临界值为0.68。根据以上结论可以看出，在未加高斯白噪声的分数阶双稳态系统中，当α大于系统的临界值时，需要一些额外的能量来驱动布朗粒子克服势垒高度；当α小于该临界值时无需外力驱使即可产生随机共振。

如图4所示为信号幅值增加至0.4时，α从0.1以0.1的步长递增到0.9的输出响应的时域图。从图4(a)中可以看出势垒高度随着幅值的增加而增大，从图4(b)中可以看出分数阶临界阶次增加至0.92。

图4 A=0.4时α变化下系统输出时域图Fig.4 Time-domain diagram of system output under the change of α when A=0.4

如图5所示，可以看出系统的临界阶次受信号幅值的影响，信号幅值越大临界阶次越大。这是因为信号幅值的大小会影响势垒高度的大小，幅值越大势垒高度越大，则系统的临界阶次也就越大。

图5 幅值与分数阶阶次临界值的关系图Fig.5 Relationship between amplitude and critical value of fractional order

4.2 加入噪声时改变分数阶求导阶次

由第4.1节可知当α大于系统临界值时，双稳态系统没有产生随机共振。基于此情况，本节将讨论向双稳态系统中加入高斯白噪声，固定噪声强度D=3.1，外加周期信号幅值A=0.3时是否能产生随机共振。

如图6(a)为固定噪声强度，不同α下系统输出的时域图。图6(b)为其对应的频谱图。可以看出当α=0.7时，布朗粒子在两势阱间做无规律运动，此时对应频谱值为0.019 96，还未达到输入信号频谱值0.025 03，称此状态为欠共振；当α增加至0.85时，布朗粒子逐渐趋于规律运动，此时的频谱值0.415 2远大于输入信号频谱值，双稳态系统产生随机共振；α继续增加至0.95后，布朗粒子又进入无规则运动，频谱值较α为0.85时反而小，称此状态为过共振。

图6 外加噪声时D不变，α变化下系统输出的时域图和频域图Fig.6 Noise is added, time-frequency diagram of system output under the change of α when D is unchanged

从图7中可以看出，双稳态系统的噪声强度固定，当α小于0.7时，功率谱值均小于0.02，甚至还未达到原始信号的功率谱；增加α的大小，功率谱值也随之增大并达到一个极大值，在此极大值处，双稳态系统产生了随机共振；继续增加α的大小，系统的势垒值也在不断增大，布朗粒子很难再翻越势阱，此时功率谱值反而减小，抑制了随机共振的产生。

图7 功率谱值与分数阶求导阶次的关系图Fig.7 Relationship between the power spectrum value and the fractional derivative order

4.3 固定分数阶求导阶次时改变噪声强度

由4.2节中可知噪声强度固定，α过小或过大时，双稳态系统均不会产生随机共振。基于此情况，本节将讨论当α=0.75时，加入噪声并且改变噪声强度的随机共振现象。

如图8(a)为固定α，不同噪声强度下系统输出的时域图。图8(b)为其对应的频谱图。可以看出当D=1.5时，布朗粒子在某一势阱中做无规律运动，此时频谱值为0.022 49，还未达到输入信号频谱值0.025 03，此时为欠共振状态；当D增加至2.2时，布朗粒子逐渐趋于规律运动，此时的频谱值0.642 3远大于输入信号频谱值，双稳态系统产生随机共振；D继续增加至5后，布朗粒子又进入无规则运动，频谱值较D为2.2时反而小，此时为过共振状态。

图8 外加噪声时α不变，D变化下系统输出的时域图和频域图Fig.8 Noise is added, time-frequency diagram of system output under the change of D when α is unchanged

从图9中可以看出，分数阶求导阶次固定，增大噪声强度，双稳态系统可以产生随机共振，但持续增大噪声强度反而会抑制随机共振的产生。当噪声提供的能量远大于布朗粒子所需翻越势阱的能量时，输出信号淹没于噪声信号中，输出信号的频谱值减小，反而不会产生随机共振。

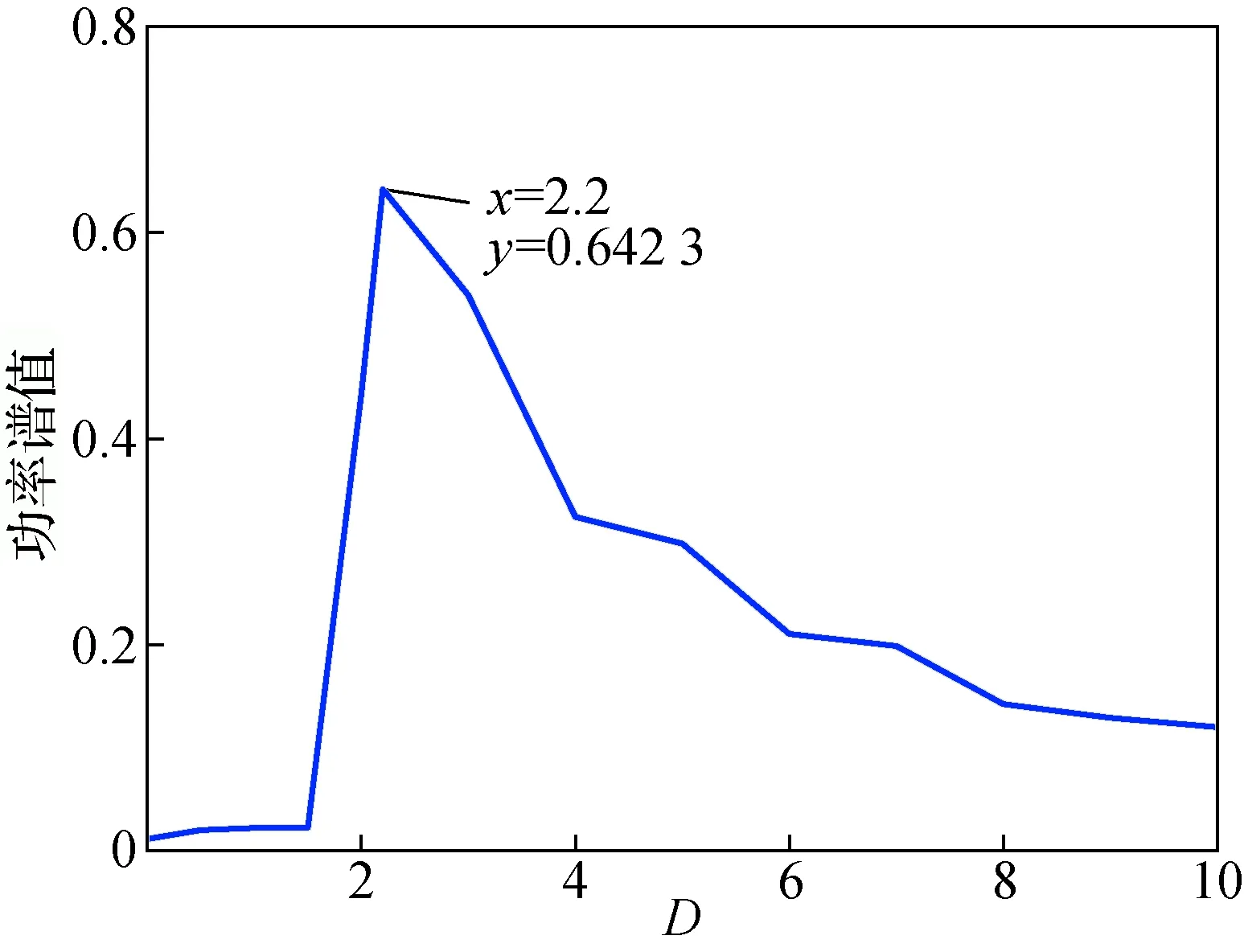
图9 功率谱值与噪声强度的关系图Fig.9 Relationship between power spectrum value and noise intensity

4 结 论

本文提出了一种基于Atangana-Baleanu分数阶微积分的双稳随机共振系统模型，利用改进的Oustaloup算法对其近似化求解，从仿真实验中可以得到以下结论：

(1) 当系统中只有微弱周期信号作用时，无需外力作用下分数阶求导阶次小于临界阶次时系统即可产生随机共振且临界阶次的大小随周期信号幅值的增大而增大；

(2) 再将高斯白噪声加入系统中，噪声强度一定时改变分数阶求导阶次，分数阶求导阶次和输出信号的频谱值呈非线性关系，存在一个最佳的分数阶求导阶次使系统产生随机共振；

(3) 固定分数阶求导阶次不变改变噪声强度，噪声强度和输出信号的频谱值呈非线性关系，存在一个最佳的噪声强度使系统产生随机共振。

综上所示证明了该方法的有效性，后续可以将其应用至轴承故障检测的实际工程中。