宽频带电磁式角振动校准系统研究进展
唐 波, 何 闻, 刘爱东
(1. 浙江大学 浙江省先进制造技术重点实验室, 浙江 杭州 310027;2. 中国计量大学 计量测试工程学院, 浙江 杭州 310018; 3. 中国计量科学研究院, 北京 100029)
1 引 言
角振动传感器广泛应用于航空航天、卫星导航和石油勘探等领域[1~3],为确保其幅值复灵敏度、相移特性和测量不确定度等指标满足出厂指标要求,需要定期对角振动传感器进行校准[4,5]。宽频带角振动台是角振动校准系统的重要组成部分,GB/T 20485.15规定了角振动校准系统的技术要求,指出其性能优劣直接影响角振动传感器校准结果的准确和量值统一。
20世纪60年代初,美国麻省理工学院仪表实验室采用精密角振动台对美国惯性仪器进行检测,促进了惯性导航技术的发展[6]。20世纪90年代,德国联邦物理技术研究院(PTB)建立了角加速度和灵敏度幅值测量不确定度为0.2%~0.5%、相移为 0.5°(k=2)国家标准装置[7,8],该角振动校准装置频率范围为0.3~1 000 Hz,最大角位移为1 rad,最大角加速度为1 400 rad/s2。韩国标准科学研究院(KRISS)对角振动校准系统的角振动台进行了广泛的研究,研制出不同位移和角加速度的角振动台[9~12],频率范围扩展到1~5 000 Hz,且最大角位移1.05 rad,角加速度可达5 000 rad/s2。美国、俄罗斯和日本等国家计量技术机构也开展了相关研究,但研究成果鲜见公开报道。北京长城计量测试技术研究所(CIMM)采用无刷电机作为角振动激励器,实现了0.1~200 Hz范围内正弦角运动量的输出[13],由于电机的电气时间常数大和转子第1阶扭振固有频率低,输出运动量的上限频率受到限制。为了提高角振动台的上限频率,文献[14]又提出一种框式结构高频角振动台,工作频率范围10~550 Hz,最大角加速度1 760 rad·s-2,角加速度波形失真度小于2%,由于采用三角支撑恢复弹簧,角位移受到限制。中国计量科学研究院(NIM)联合浙江大学(ZJU)对角加速度激光校准方法基础理论和角振动校准装置展开研究,有望解决各类旋转角振动传感器的量值溯源问题。本文在总结角振动校准系统特点的基础上,对其角振动台类型及技术指标进行系统阐述。
2 角振动传感器的校准原理及方法
为了满足角振动传感器校准的规范和统一,ISO 16063-15-2006[4](GB/T 20485—15—2010[5])规定了绝对法校准角振动传感器的仪器设备和操作流程,以及采用稳态正弦振动和激光干涉测量法[15]获得角振动传感器灵敏度幅值和相移的方法。根据激光干涉仪输出信号的不同处理方式可分为:条纹计数法、最小点法和正弦逼近法。条纹计数法[16,17]适用于频率范围为1~800 Hz的灵敏度幅值校准,一般可测量的最小位移幅值为2 μm(后向反射器或衍射光栅放于离转轴50 mm处),若采用特殊方法减小量化误差措施,可用于更小幅值、更高频率指定角加速度幅值(如1 000 rad/s2)的情况下进行校准,由于该方法通过计条纹数来测量位移,而不能检测相位的变化情况,因此不能进行相位校准;最小点法[18,19]适用于频率范围为800 Hz~1.6 kHz的离散幅值点上灵敏度幅值校准,由于该方法采用第一类一阶贝塞尔函数零点对应的自变量值来确定位移,因此需要在固定的角位移幅值进行校准,其角速度和角加速度随着频率的改变而变化,同样也不能进行相位校准;而正弦逼近法[20,21]以最小二乘法为核心,通过相位展开、正交光电信号处理和动态相位解调等技术,解算出角振动传感器灵敏度的幅值和相移,由于正弦逼近法能同时校准灵敏度幅值和相移,Martens H J V等[22]提出了一种基于正弦衍射光栅的激光干涉角运动量测量方法,当扩展因子为2时的幅值和相位扩展不确定度分别为0.2%~0.5%和0.2°~0.5°。
激光干涉法绝对测角方法有2类:一类是基于后向反射器的A类激光干涉测量方法;另一类是基于正弦衍射光栅的B类激光干涉测量方法。
2.1 基于A类激光干涉测量方法的校准系统
基于A类激光干涉角振动测量方法的校准系统如图1所示,调整干涉仪到最佳状态,在规定的振动频率和幅值条件下,对角振动传感器的灵敏度幅值和相移进行测量。

图1 A类激光干涉仪角振动测量系统Fig.1 Angular vibration primary measurement system of A-type laser interferometry
信号发生器输出的正弦电信号经功率放大器放大后驱动角振动台运动;将角振动传感器安装在台面轴心上,输出的信号经放大器放大后输入到高速高精度数据采集卡中实时采集并将结果输入到PC机中;将后向反射镜安装在角振动台台面指定半径上,采用激光干涉仪对反射镜的线位移进行测量,进而计算得到角位移。
为了求得振动台输出运动量的幅值和相位,采用2个光电接收器分别检测两路相位差90°的干涉信号,然后两路光电信号被高速高精度数据采集卡采集并传输到PC机中的专用数据处理程序进一步处理(包括正弦逼近法)得到角振动台输出角位移、角速度和角加速度;最后将角振动传感器输出的电压量与角振动台输出的运动量进行计算处理可得角振动传感器灵敏度幅值和相移参数。随着角位移的增大,后向反射镜无法接收或反射激光光路,使得该方法检测角位移受到限制,该方法可测的最大角位移(峰峰值)为0.052 rad。
2.2 基于B类激光干涉测量方法的校准系统
当角位移(峰峰值)大于0.052 rad时,为了克服A类激光干涉测量角位移的限制问题,可采用B类激光干涉测量方法,基于B类激光干涉角振动测量方法的校准系统如图2所示。B类测量方法与A类测量方法的主要区别是采用衍射光栅代替后向反射镜,衍射光栅安装在台面的侧向环面上,如果衍射光栅沿整个圆周分布,则检测角度理论上可达 2 π rad。

图2 B类激光干涉仪角振动测量系统Fig.2 Angular vibration primary measurement system of B-type laser interferometry
由这两类角振动校准系统可以看出:角振动校准装置包括角振动台、激光干涉仪、被校角振动传感器以及信号解算和处理软件,其中角振动台用于产生低失真的稳态正弦角振动,是确保角振动校准装置量值精准复现的先决条件和重要保障。
3 角振动台研究现状
1975年美国报道了一种角振动台[23],可用于校准角位移、角速度和角加速度传感器,能在不同的频率点上提供常峰值振幅,如常峰值角速度或常峰值角加速度,振动频率范围为0.2 Hz~100 Hz,振幅极限为±0.52 rad。
1993年PTB提出了一种盘式动圈的角振动台如图3所示[24],采用了轴向磁通的磁路结构,气隙磁场由永磁体产生,位于气隙磁场中的动圈通入交变电流后,动圈导线受到安培力的作用而发生转动。为了减小摩擦力对运动部件的影响,运动部件采用了气浮轴系导向。

图3 PTB角振动台样机Fig.3 Angular vibrator prototype in PTB
2006年国际标准组织ISO 16063-15-2006提出了关于绝对法校准角振动传感器的角振动激励器如图4所示,当带电载体切割磁场时,洛伦兹力对其产生作用,线圈的扭矩通过运动轴传递到测量台面上,安装在测量台面的角振动传感器受到激励而输出信号,台面侧面向安装有衍射光栅,配合激光干涉仪可测量运动部件输出的角动量。

图4 ISO角振动台原理示意图Fig.4 Schematic diagram of angular vibrator in ISO
2007年KRISS根据国际标准组织ISO 16063-15-2006对角振动传感器绝对校准推荐的角振动激励器类型研制出一种盘式动圈角振动台如图5所示[9~12]。

图5 KRISS的角振动台样机Fig.5 Angular vibrator prototype in KRISS
2007年CIMM提出了一种框式动圈的角振动台如图6所示[25],主要有工作台面、空气轴承、激磁线圈、框式动圈和激磁回路组成。研制出的角振动台工作频率范围为10~550 Hz,最大角加速度为1 760 rad/s2。

图6 CIMM的框式角振动台Fig.6 Angular vibrator of frame-type in CIMM
为解决国内角振动量值无法溯源、测量频率范围窄、量值精度不高的问题,NIM联合ZJU[26,27]承担了0.000 5~1 200 Hz角振动基准装置配套的宽频带角振动台研制任务,研制的低频和中频标准振动台如图7所示,其中低频角振动台装置最大角位移(峰峰值)为5.23 rad,中频角振动装置最大角位移(峰峰值)为1.04 rad,角加速度范围为0.04 rad/s2~2 000 rad/s2。该校准装置角加速度复灵敏度测量不确定度(k=2):参考点优于0.5%,0.5°,通频带优于1.0%,1.0°。

图7 ZJU研制的角振动台样机Fig.7 Angular vibrator prototype in ZJU
4 宽频带角振动台的关键技术
宽频带角振动台是一种特殊的有限角旋转电机,主要由运动部件、空气轴承和永磁体磁路和平衡位置弹性支撑装置组成。假设角振动台运动部件视为刚性旋转体,其机电耦合动力学模型可简化为如图8所示。

图8 机电耦合模型Fig.8 Electromechanical coupling model
根据基尔霍夫电压定律和牛顿第二定律可联立角振动台的机电耦合方程为:
(1)

假设式(1)的参数均为常数,且电流i和角位移θ的初始条件为零,角振动台输出的角位移与输入电压的传递函数为:
(2)
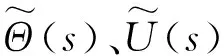
由式(2)可见:输出角位移除了与输入的电压量有关外,还与动圈参数、气隙磁感应强度、运动部件的转动惯量、弹性装置的刚度系数和阻尼系数等有关。当输入电压信号为无失真的正弦信号时,满足式(2)的角振动台就能输出无失真的角位移。然而,式(2)的角振动台运动部件并非绝对刚性旋转体,式(2)中的其它参数也并非绝对常数,从而导致角振动台输出波形产生失真。为了解决非线性失真问题,输出高质量的角振动量以满足角振动校准的要求。为此,宽频带角振动台需解决如下3项关键技术:1)高扭振频率的运动部件设计技术;2)强而均匀的气隙磁场磁路结构设计技术;3)可调电粘弹性支撑装置设计技术。
4.1 高扭振频率的运动部件设计技术
运动部件是角振动台用来传递运动和能量的关键部件,为有效地将动圈产生的转矩传递到工作台面,必须使得运动部件的第1阶固有扭振频率尽可能高,从而有利于降低运动部件在工作频率范围之内的波形失真度,进而提高角振动台的上限工作频率。
针对低频和中频角振动台不同工况的特点,对于低频角振动台,工况要求输出大转角和大承载,则要求运动部件的转动惯量尽量大;对于中频角振动台而言,工况要求小角位移和大角加速度,则要求运动部件的转动惯量尽量小。因此,运动部件设计过程中需要考虑如下因素[28]:工作频率范围、输出角运动量、工作台面尺寸和承载能力,在此基础上提出运动部件拓扑结构,建立集总参数运动部件动力学方程,分析影响运动部件第1阶固有扭转频率和转动惯量的主要因素。为了更准确地分析运动部件的动力学特性,采用有限元分析法求解运动部件的模态解,并对运动部件的模态进行优化,如材料组合、结构优化、尺寸变化等措施,优化后得到的第1阶固有扭振频率1 234.3 Hz和运动部件转动惯量 321.9 kg·mm2。
4.2 强而均匀的气隙磁场磁路结构设计技术
气隙磁场是角振动台机电能量转换的重要载体,按照气隙磁通方向分类:轴向气隙磁通和径向气隙磁通,因此角振动台的磁路结构根据不同工况要求选用合适的磁路结构。
对于中频角振动台,要求小转动惯量和大角加速度,其结构需要设计成紧凑型,轴向气隙磁通正好具有高磁感应强度和高功率密度的特征,其磁路结构被ISO 16063:2006推荐为标准角振动台的磁路。对于低频角振动台,要求大负载和大角位移,其结构较大,需采用框式动圈结构,为此需采用径向气隙磁通结构。在两种磁路结构设计时,需要考虑的因素有[29,30]:输出运动量参数、功率放大器的电流输出能力,动圈工作状态下的发热情况等,然后基于等效磁化强度法分别建立直角坐标系下和极坐标系下的磁路参数与气隙磁感应强度数学方程,分析永磁体几何参数、气隙高度及其他因素对气隙磁场的影响,在此基础上采用三维电磁场有限元模型对其磁路结构进一步优化和验证,优化后得到的强而均匀气隙磁感应强度均值0.72 T和不均匀度1.9%。
4.3 可调电粘弹性支撑装置设计技术
弹性支撑装置在角振动台中用于将旋转运动部件始终保持在运动平衡位置,常用的弹性支撑装置有扭簧或软胶管组成。当输出小角位移运动量时,变形量在弹性装置的线性范围内,弹性装置的刚度系数及阻尼系数均为常数,图8中的输入电压和输出角运动量呈线性关系;然而,当角振动台输出较大角位移时,弹性装置的非线性将体现出来,如刚度系数将随着位移的增大而发生变化,特别是大角度旋转可能导致的弹性元件缠绕,使得非线性更加突出。由式(2)可知,当输入某一个频率的正弦电压时,角振动台将输出带有该频率谐波的非正弦角运动量,从而引起角振动台输出波形的失真。为了解决大角位移弹性支撑问题,去除了机械弹簧机构,采用一种电粘弹性支撑装置,如图9所示。该装置为一种位移、速度反馈控制系统:角位移信号θ一方面经可调放大器1处理,另一方面经微分器和可调放大器2处理,然后将两路信号通过加法器相加,再与信号发生器输出的标准信号进行求差运算,所得偏差信号经过比例放大器处理后输出给功率放大器,最后驱动角振动台运动。

图9 电粘弹性支撑装置结构框图Fig.9 Structural block diagram of electro-viscoelastic-suspension device
根据图9可得角振动台电粘弹性支撑控制系统的闭环传递函数为:
(3)
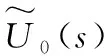
比较式(3)与式(2)可知,当JR≫cL时,当调节式(3)中的参数k1和k2,相当于调节式(2)中弹性装置的刚度系数k和阻尼系数c,也就是说采用电参数代替了机械接触式弹性支撑装置的刚度和阻尼系数,所以该可调电粘弹性支撑装置的刚度和阻尼系数不受限于角位移,并且是线性可调的,从而改善了输出波形的失真度,可保证全频段加速度波形失真度低于1%。
5 结 论
根据国际标准ISO 16063-15-2006和国标GB/T 20485—15—2010关于绝对法校准角振动传感器的测量方法,发现高质量的稳态正弦角振动激励源对角振动测量结果的准确性至关重要,但是我国对其所涉及的关键核心技术尚未全部掌握,通过借鉴德国联邦物理技术研究院(PTB)和韩国标准科学研究院(KRISS)关于角振动校准装置的成功经验,有助于我国快速建立起角振动国家计量基准。
本文通过对角振动台国内外研究现状进行了综述,鉴于电动式角振动台具有电气时间常数小,响应速度快、上限频率高等特点,可实现宽频带低失真的角振动输出。针对现有角振动台存在的精度低和线性差的特点,对其所涉及的高扭振频率运动部件设计技术、强而均匀的气隙磁场磁路结构设计技术及可调电粘弹性支撑装置设计技术等关键技术进行了深入分析,并给出如下研究建议:运动部件是角振动台用来传递运动和能量的关键部件,应使运动部件的第1阶固有扭振频率尽可能高;气隙磁场是角振动台机电能量转换的重要载体,应使气隙磁场尽可能强而均匀;弹性支撑装置用于将旋转运动部件始终保持在运动平衡位置,采用可调电粘弹性支撑装置的刚度和阻尼系数代替传统机械接触式弹性支撑装置的刚度和阻尼系数,降低输出角振动波形的失真度。

