指向整体结构的小学数学习题设计

余慧

（古田县教师进修学校，福建 宁德 352200）

数学知识具有很强的内在逻辑，是整体的、系统的、结构的。［1］指向整体结构的数学习题，对数学知识进行条理化、模块化、网络化的整理和架构，帮助学生突出知识结构，完善认知结构。指向整体结构的数学习题是结构化教学的载体。笔者尝试在小学数学习题中孕育结构，让学生在读题解题的同时对自身的知识结构和认知结构进行重新架构。文章将从习题设计上突出知识结构和解题过程中完善认知结构两个方面阐述笔者在小学数学习题设计方面的实践探索。

一、习题设计上突出知识结构

数学知识结构是由知识之间内在的逻辑联系联结而成的知识整体。［2］教师着意设计突出知识结构的习题，帮助学生把零散的、相关联的、易混淆的知识串线联网，学生在不知不觉中把知识系统化。习题是一种精美的语言，它能用简单的数字、字母、符号、图表等进行排列组合，将实际问题中复杂的数量关系表示出来。指向整体结构的习题能帮助学生将所学知识结构化。

（一）运用符号关联

符号是数学最简洁抽象的语言，也是数学学习最常用的工具，数学表达和数学思考更是少不了符号的运用。教师在练习中引导学生运用符号表示数量关系和逻辑关系，使学生经历环环相扣的抽象过程，获得对数学知识脉络化的理解。

样题1：我们已经学习了很多常用的计量单位，如货币单位、质量单位、长度单位、面积单位、体积单位等。你能用双箭头符号表示单位之间的进率关系吗？如（图1）：

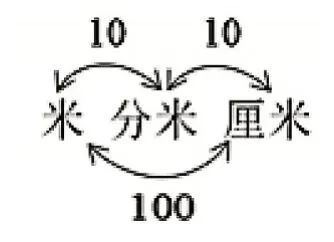
图1

系统的知识需要结构化的表达。［1］箭头符号可以将抽象的、散点的知识形象化、条理化、逻辑化。它可以把相关元素串成线，把枯燥的练习过程变得鲜活可亲。用双向箭头符号关联三组进率：米和分米、分米和厘米、米和厘米之间的关系，从简单结构到复杂结构的表达方式将三组进率关系有机统一，并迁移到其他单位进率的学习。运用双向箭头更加突出单位之间进率的关系，环环相扣提示学生进行完整的思考，感悟计量单位之间的逻辑体系，轻轻松松就可以理解单位之间的进率关系。

（二）借助表格对比

小学数学教学经常使用表格，无论是探究新知，还是巩固练习，或是单元复习整理，经常会让表格来“说话”。在习题设计中借助表格这个形象直观的载体，能够清晰明了地展示丰富的数学信息，形成强烈对比，启发学生思考，使学生自主架构知识体系，更好地理解数学，成为学习的主体。

样题2：分数、小数、百分数的互相改写（表1）。

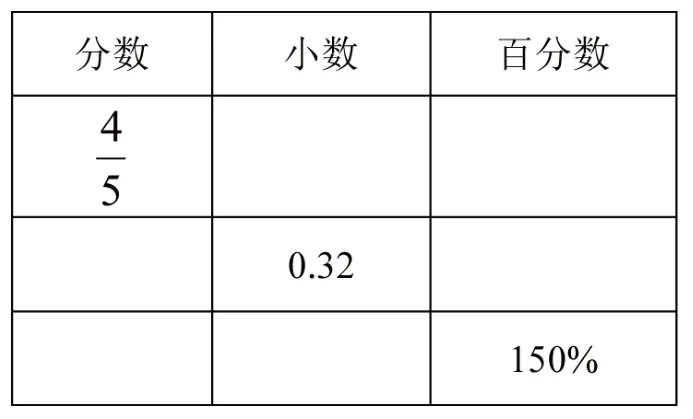
表1

在数与代数领域，分数、小数、百分数是非常重要的数概念。这些概念之间本质上有深刻的联系，却又不尽相同。对这样的概念采用表格纵横关联相对比，有助于学生对知识产生结构性的理解。学生借助表格对比很容易找出三个数概念之间的异同点，引导学生对散点分布的数概念进行系统的整理。

（三）引入集合感悟

集合图能简单明了地表示概念间的相互关系，引入集合图是揭示概念本质属性的一种好方法。在习题设计中引入集合图，既可以帮助学生揭示知识整体和部分关系，又可以使学生掌握个性与共性的关系。在对概念有了更深刻全面理解的同时，感悟集合思想的简洁性，积累集合思想的活动经验。

样题3：请你根据长方形、正方形、平行四边形之间的关系填写韦恩图（图2）。

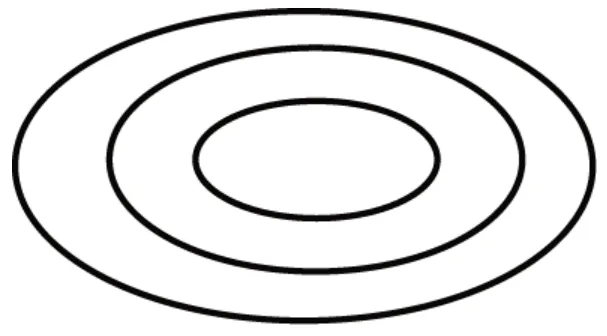
图2

在平面图形的教学中，长方形、正方形、平行四边形是具有很多共同特征的平面图形，它们之间具有包含关系。在习题设计中引入韦恩图，既直观形象地帮助学生理解长方形、正方形、平行四边形各个概念之间的联系和差异，又能培养学生的整体意识。这样结构化的表达方式有利于学生对集合思想的深入理解与感悟。

（四）编织导图沟通

思维导图在小学数学复习课一直特别受青睐。数学知识讲究系统性，在习题中引导学生自主整理，上下沟通，左右链接，编织属于自己的知识网络体系，能系统地认识知识各部分之间的联系。

样题4：看图（图3）填空，说一说每种三角形的特征，想一想每个三角形至少有几个锐角？

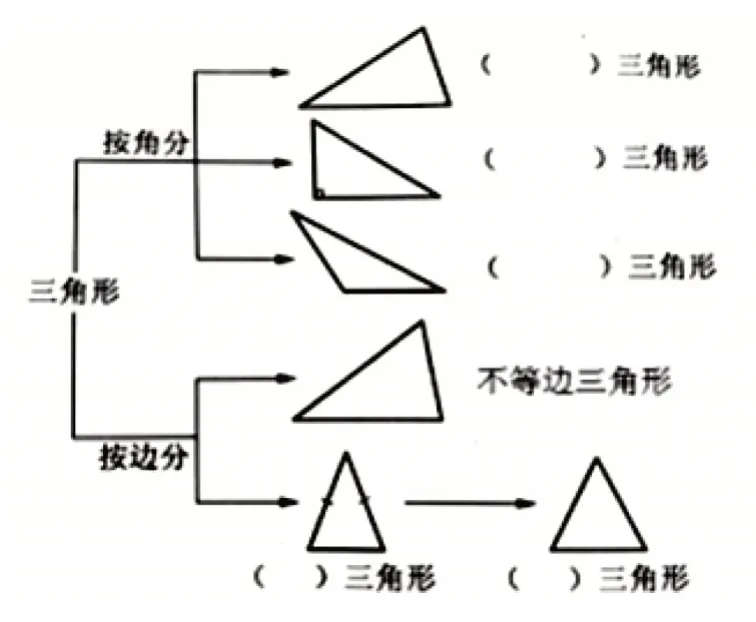
图3

在认识三角形的分类之后，教师巧妙地运用练习引导学生在整体知识的背景下对三角形的知识进行系统的整理和内化。在解题过程中要求学生把三角形按角和边分成两类，根据三角形的特征重新组织，编织成一张思维导图，这种突出知识结构的导图有助于沟通三角形之间的关系，也有助于学生更高站位地对三角形知识进行整体架构。

二、解题过程中完善认知结构

数学认知结构是一个充满内部联系的并按一定规律组成的层次分明的结构。［3］系统的知识结构必须通过学生积极加工、内化吸收才能转化为认知结构，新的学习内容与学生原有的认知结构顺利接轨才能生成新的认知结构。精心设计立意高远、内涵丰富并能呈现知识之间纵横关系的习题，学生在解题过程中不断分析比较，按知识逻辑重新拆分组合，完成对知识结构和知识呈现顺序的深度融合。这种孕育整体结构的习题，对完善学生的认知结构有重要的指导意义。

（一）揭示知识本质特征

数学知识有着严密的逻辑结构，其纵深发展都是一条有机的知识链，每个知识点在知识链上都能找到相应的位置。每个单元新知识教学完成之后，教师设计有整体结构的习题，能引导学生整理发现所学知识间的内在本质和逻辑顺序，理清新知与旧知的相互联系，揭示知识本质上的相同之处。

样题5：龙龙学习了《分数加法和减法》这一单元，他认为分数加法和减法的计算方法，其实与整数加、减法以及小数加、减法的计算方法是一样的。你同意龙龙的说法吗？请你用举例的方法说明理由。

学习加减法计算，从整数加减法开始，到小数加减法和分数加减法，它们的知识本质特征是相同的，计算方法是一致的，都是相同计数单位上的数相加减。在这个前提条件下，才有了具体运算法则上的大同小异。学生在解题过程中分析比较与其他运算法则的区别与联系，使知识的逻辑与学生的认知规律相结合，学生获得的算法不再是生硬的文字规则，而是算理算法相融的深刻领悟。

（二）展示知识形成过程

良好的数学认知结构中所包含的知识是具有丰富的感知体验、深刻内化的知识。要完善学生的数学认知结构，必须找到知识的生长点，整合知识形成的过程，将学生的思维过程可视化。设计展示知识形成过程的习题，在解题过程中学生瞻前顾后体会知识生成的来龙去脉，提高学生把知识结构转化认知结构的能力。

样题6：亮亮整理了小学四年以来学过的乘法笔算方法如下（图4）：

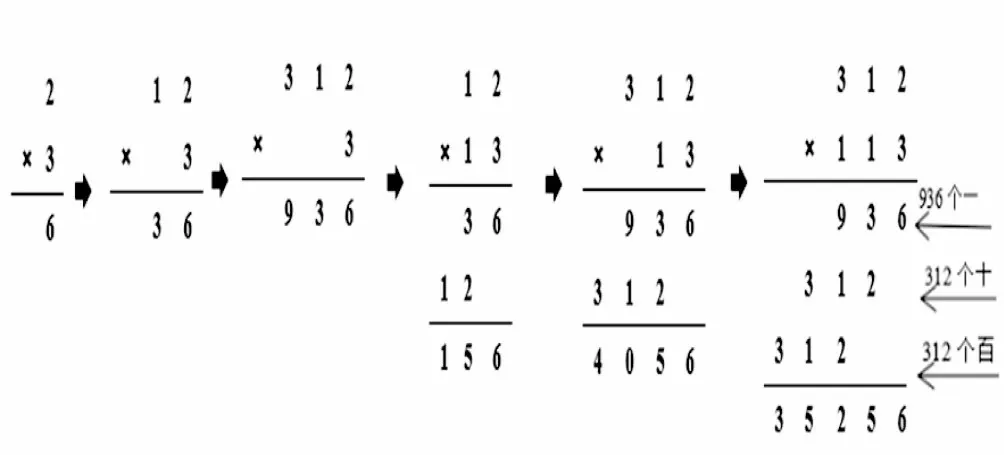
图4

通过整理，亮亮有了新的想法：数学其实挺简单的！从乘数是一位数的乘法到乘数是多位数的乘法，它们的计算方法其实都一样，都是拆一拆、算一算，一共有几个一、几个十、几个百……你觉得亮亮的想法有道理吗？你能结合上图说说312×113 的计算过程吗？

学生回顾笔算多位数乘多位数知识的形成过程，头脑里自然而然形成融会贯通的有生长力的知识网络，实现学习的正迁移。整个解题过程，就是数学知识结构和学生认知结构相互作用的过程，二者共同促进思维结构的发展，提高了学生的学习力。

教师只有精心设计，帮助学生突出知识结构，完善认知结构的习题，才能引领学生从知识整体性的高度建构，才能让小小习题拥有大结构的格局，闪耀大结构的光芒。