构造一个具有拟凸性和拟齐次性的拟距离∗

余安康，李宝德

(新疆大学 数学与系统科学学院，新疆 乌鲁木齐 830046)

0 引言

作为欧氏距离的推广,拟距离可以应用在更广泛的情况下,例如在各向异性情形下的拟距离仍然具有很多良好的性质,具体内容可参阅文献[1]和[2].对于欧氏空间中凸体所满足的几何性质（定理1）的一种推广,我们称用距离定义的球满足与凸体类似的几何性质为该拟距离的拟凸性.这种定义灵活方便,所建立的性质也可在更广泛的情况下使用.此外,拟齐次性是拟距离所定义的球的性质,该性质是对欧氏空间中球的基本性质的一种推广,也具有一些良好的性质.例如,欧氏空间中的任意范数所构成的拟距离满足拟齐次性,并且满足拟齐次性的拟距离也一定满足双倍条件（见公式(4)）.于是一个自然的问题,在欧氏空间中,是否有一些非平凡的拟距离满足拟凸性和拟齐次性? 本文的目的便是构造一个满足拟凸性和拟齐次性的非平凡的拟距离.受Stein[3]的启发,本文证明了由向量场X1:=∂/∂x1和X2:=所导出的映射满足上述两个性质的拟距离.

为方便起见,对全文做如下约定.符号D ≾F 表示D ≾CF,其中C 为一个正的常数.如果D ≾F 且F ≾D,我们记为D ∼F.

1 拟距离，拟凸性和拟齐次性

Rn中的椭球ξ 是指n 维欧氏空间的单位球Bn:={x ∈Rn:|x|<1} 在仿射变换下的像集,即

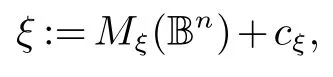
其中:Mξ是一个非奇异矩阵,cξ∈Rn是椭球ξ 的中心.对任意的椭球ξ 和λ ≥1,定义

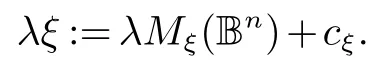
定义1集合X 上的映射ρ:X×X →[0,∞) 是拟距离,如果对所有的x,y,z ∈X 满足如下条件:

(i) ρ(x,y)=0 ⇔x=y;

(ii) 存在常数C>0,使得ρ(x,y)≤Cρ(y,x);

(iii) 存在常数κ ≥1,使得ρ(x,y)≤κ(ρ(x,z)+ρ(y,z)).

显然,条件(ii) 成立当且仅当ρ(x,y)∼ρ(y,x).另外,设=[ρ(x,y)+ρ(y,x)]/2,可进一步得出

Rn中的凸体指的是一个内部非空的紧凸集.John 已经证明了对于Rn每一个凸体都包含一个体积最大的椭球[4].这个椭球按维数n 倍膨胀也可以包含原来的凸体,详细内容参阅文献[5]和[6]中的定理3.13.

定理1K ⊆Rn是一个凸体.则存在一个唯一的体积最大的椭球ξ ⊆Rn使得ξ ⊆K 且K ⊆n·ξ.

受定理1 的启示,我们可以推广凸体的概念.

定义2设常数Q ≥1.称K′⊆Rn关于x ∈K′是Q-拟凸的,如果存在一个以cξ=x 为中心的椭球ξ ⊆Rn使得

由定理1可知,任意一个Rn中的凸体是Q-拟凸的,这里Q=n.值得注意的是我们在上面的定义中没有假设唯一性,这说明对于任意给出的一个集合K′,可能存在两个不同的椭球(即使是最大体积) 满足(1).

定义3给一个拟距离ρ:Rn×Rn→[0,∞).称ρ 满足拟凸性质,是指存在一个常数Q ≥1 使得对任意的x ∈Rn和r>0,球

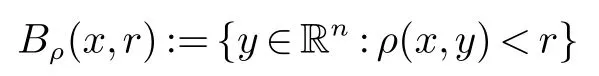
定义4称Rn上的拟距离ρ 满足拟齐次性质,是指存在两个正的常数a=a(ρ) 和b=b(ρ) 满足对任意的x ∈Rn,r>0 和λ ≥1,有

显然,欧氏空间中的任意范数所构成的拟距离满足拟齐次性质,此时,a=b=1.此外,拟齐次性质也是一种比双倍条件[7]更强的条件,由拟齐次性我们可以立即得出

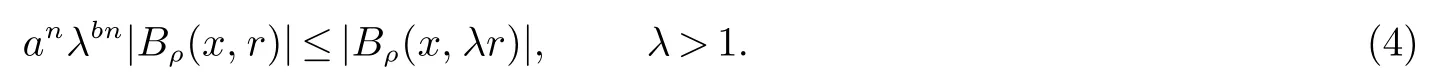
2 一个满足拟凸性质和拟齐次性质的拟距离的例子

构造这个例子的动机来自于Stein.设k 是一个非负整数,并且对任意的x ∈R2和δ>0,定义

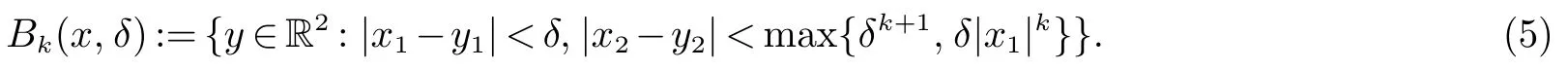
则球族{Bk(x,δ):x ∈R2,δ ∈(0,∞)} 是一个相关向量场X1:=∂/∂x1和X2:=自然导出的球族.这种球Bk(x,δ) 也可以被定义为

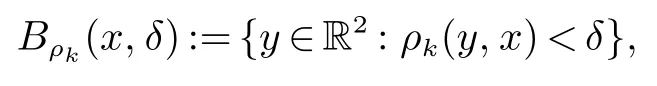
其中

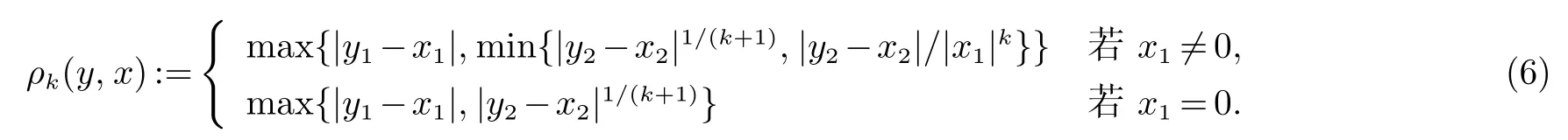
定理2设k 是一个非负整数并且定义ρk如(6) 所示.则ρk是一个满足定义1的拟距离且满足拟凸性质和拟齐次性质.

证明若假设ρk是一个拟距离,则不难验证它是满足拟凸性质和拟齐次性质.事实上,由于所有的球都具有(5) 中的形式,则无论是|x1|≥δ 或|x1|<δ,这些球实际上是长方体,一种特殊的凸体.由定理1可知,ρk满足拟凸性质并且Q=n.此外,对任意的λ ≥1,δ>0 和x ∈R2有

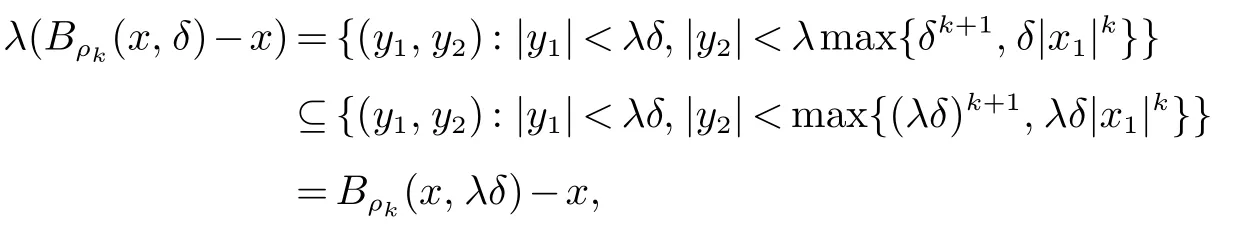
当我们取定义4 中的a=1 和b=1 时,也就证明了拟距离ρk满足拟齐次性质.

接下来,我们只需要证明ρk是一个拟距离.由ρk的定义,我们知道ρk(x,y)=0 ⇔x=y 是显然成立的,下面我们分两步来验证ρk满足拟距离剩下的两个条件.

第一步:证明ρk(x,y)∼ρk(y,x).我们仅证明下面三种典型情形,其它情形是相似的.

情形(1).对任意x=(x1,x2),y=(y1,y2)∈R2且x1,y1/=0,如果

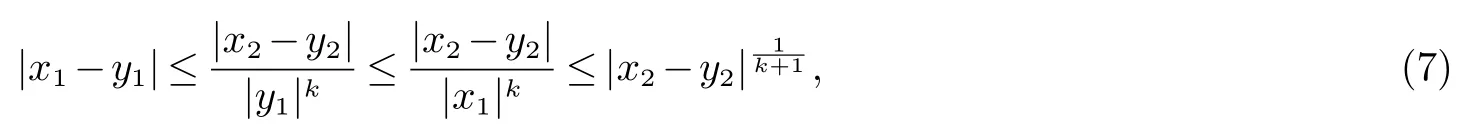
则有

现在证明存在常数C>0 使得ρk(y,x)≤Cρk(x,y),即|y1|≤C|x1|.我们使用反证法.如若不然,对任意的正整数n ≥3,存在两组向量和简记为(x1,x2) 和(y1,y2),满足(7) 和|y1|>n|x1|.因此,有

以及

此外,由|y1|>n|x1| 和n ≥3 可得

由此式,|x1|≤|y1| 和(8) 得到

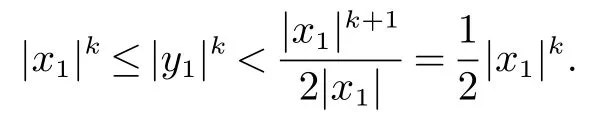
情形(2).对任意x=(x1,x2),y=(y1,y2)∈R2且x1,y1/=0,如果

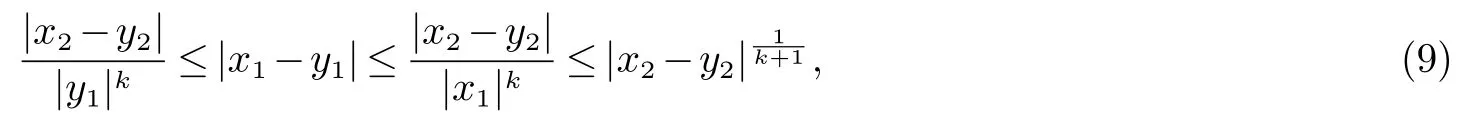
则有

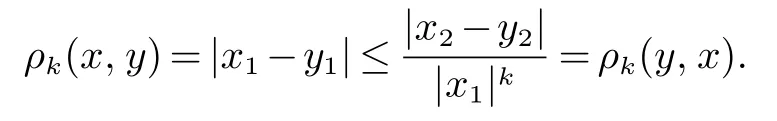
接着证明存在一个常数C>0 使得ρk(y,x)≤Cρk(x,y).使用反证法,如若不然,对任意正整数n 满足n1/k>2,存在两组向量和简记为(x1,x2) 和(y1,y2),满足(9) 和

进一步由

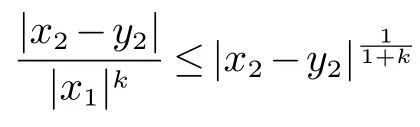
知

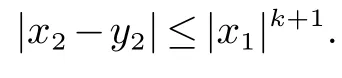
由此式和(9) 可知

通过式(9) 和(10) 得出

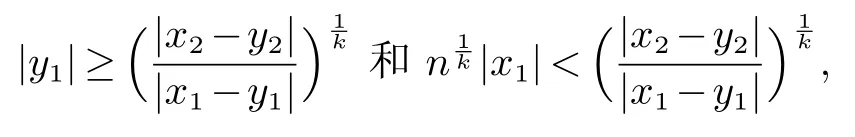
因此有|y1|>并且

由此式和(11) 得出|x1|<|x1|,矛盾!

情形(3).对任意x=(x1,x2),y=(y1,y2)∈R2且x1,y1/=0,如果

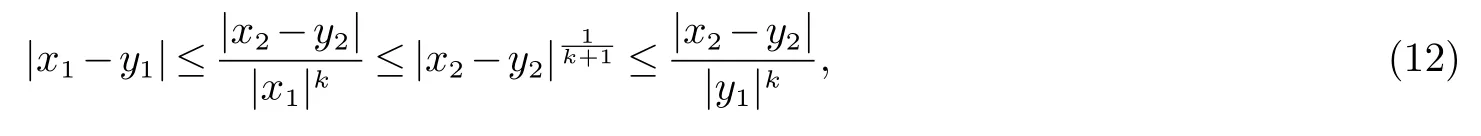
则有

同样地,我们接下来证明存在一个常数C>0 使得ρk(x,y)≤Cρk(y,x).使用反证法,若对任意一个正整数n 满足n1/k>2,存在两组向量和简记为(x1,x2) 和(y1,y2),满足(12) 和

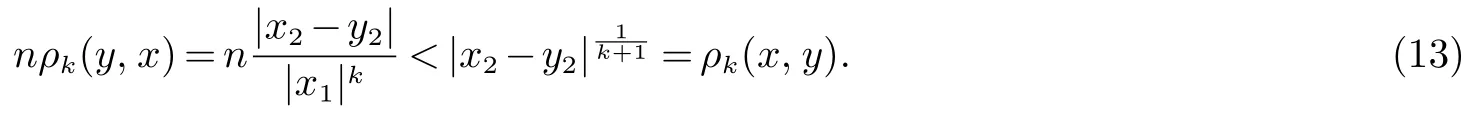
通过式(12) 和(13),有

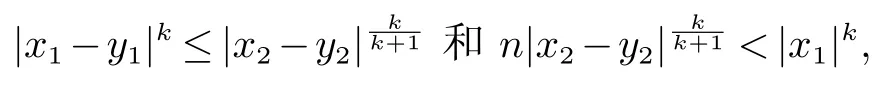
因此,

由|x2−y2|1/(k+1)≤|x2−y2|/|y1|k知

再结合n|x2−y2|k/(k+1)<|x1|k,可得出

因此,由式(14),(15) 和n1/k>2 可得

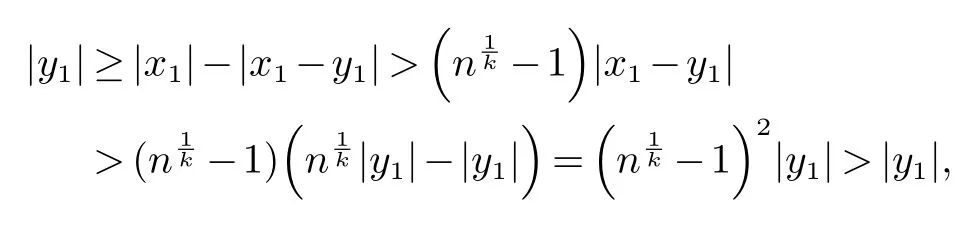
即|y1|>|y1|,矛盾!

第二步:证明ρk 满足拟三角不等式.我们只在下面两个典型的情况下证明,其它的情况是相似的.

情形(1).对任意x,y,z ∈R2且x1,y1,z1/=0,如果满足

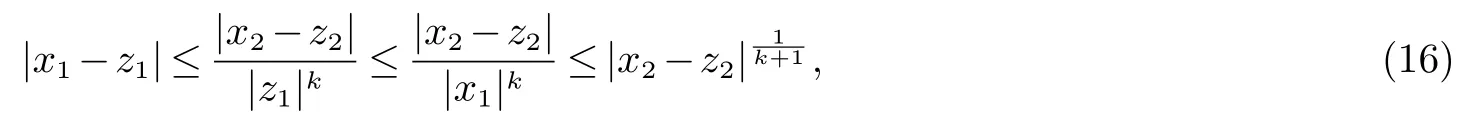
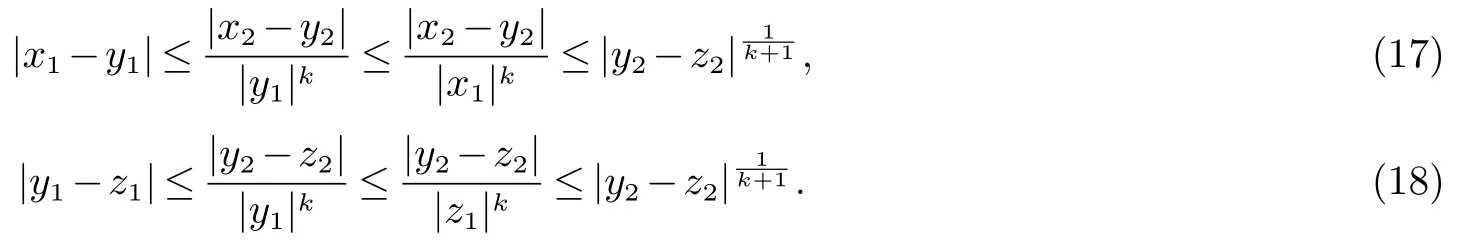
则对于式(18),使用第一步中情形(1)的估计,存在一个常数C ≥1 使得|y1|≤C|z1|.通过此式,(16),(17) 和(18)可得

拟三角不等式得证.

情形(2).对任意x,y,z ∈R2且x1,y1,z1/=0,如果满足

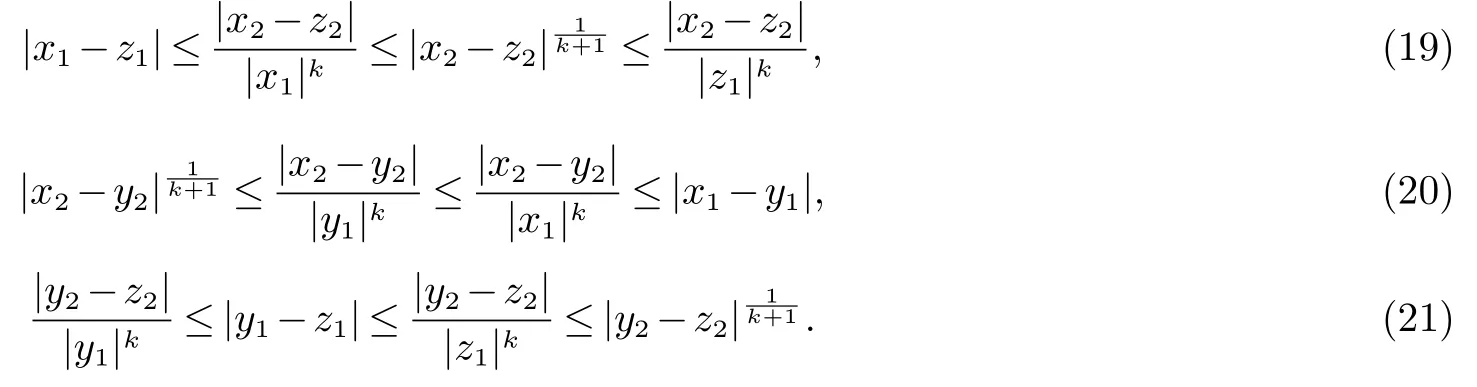
则对于式(19),使用第一步中情形(3)的估计,得到

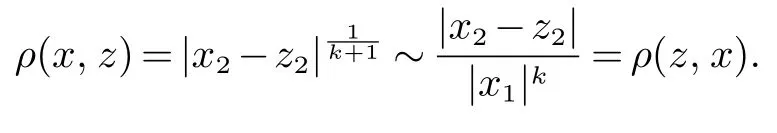
通过此式,式(20),|z1|≤|x1| 和 式(21),存在一个常数C ≥1 使得

拟三角不等式得证,我们也完成了定理2 的证明.