每个点的度数被3整除的生成母图∗

熊玮，张启慧

(新疆大学 数学与系统科学学院，新疆 乌鲁木齐 830046)

0 引言

令G是一个简单无向图，用V(G)和E(G)分别表示图G的顶点集和边集.经过G的每条边的迹称为G的Euler迹，G的环游是指经过G的每条边至少一次的闭途径.欧拉环游是指经过每条边恰好一次的环游，包含欧拉环游的图称为欧拉图，欧拉图的度能被2整除.包含所有点的欧拉子图称为欧拉生成子图.例如文献[1]研究了Hamilton图的生成子图问题.若一个图不是欧拉的，也不含有生成欧拉子图，则考虑它是否可以加边成欧拉图，即欧拉生成母图.例如文献[2]研究了欧拉母图的树数条件.类似于欧拉生成母图的研究，我们首次研究度能被3整除的生成母图.

本文研究的内容是一般图以及树图是否存在度能被3整除的生成母图.随着图阶数的增加，每个图的度能被3整除的生成母图不唯一，所以研究增加边数最少满足要求的生成母图很有意义，即最优生成母图的构造.

1 各图类度能被3整除的生成母图

图G的顶点v的度记为dG(v).称G′是G的生成母图，如果V(G′)=V(G)，E(G′)⊇E(G).若H是G的子图，G中H的补图是指子图G−E(H)，记为H(G).包含G的每个顶点的路称为G的Hamilton路，G的Hamilton圈是指包含G的每个顶点的圈，包含Hamilton圈的图称为Hamilton图.未给出的术语见文献[3].

定义1一个图G的能被3整除的最优生成母图是指图G加最少的边得到的度能被3整除的生成母图，以下简称为最优母图.

定义2定义符号[d(v)]3，用来表示将顶点v的度增加至和d(v)最相近且大于d(v)的3的倍数.

定理[3]1设G为任意无向图，|E(G)|=ε，则

命题[3]1树Tn至少有两个一度顶点.

Dirac’s定理[3]若G是简单图且|V(G)|≥3，δ(G)≥，则G是哈密尔顿的.

Tutte’s定理[3]记O(G)为G的奇分支的个数，G有完美匹配，当且仅当O(G−S)≤|S|，∀S ∈V(G).

图G的阶数n<4时，∀v ∈G，maxdG(v)<3，所以没有度能被3整除的生成母图.因此本文只考虑图的阶数n ≥4的情形.

图G增加最少的边得到度能被3整除的生成母图，即每个顶点增加最少的度.在构造图G的度能被3整除的生成母图时，设v ∈V(G)，将顶点v的度增加至和d(v)最相近且大于d(v)的3的倍数，记为[d(v)]3，若此时能生成度能被3整除的生成母图，该母图是图G的最优母图；若此时不存在度能被3整除的生成母图，考虑将其中一个顶点增加至[d(v)]3+3度时是否存在满足要求的生成母图，若不存在就按上述方法继续进行构造.

图的每个顶点v的度增加至3度时存在生成母图，则该生成母图是3正则图，显然3正则图是最优母图.

1.1 一般图度能被3整除的生成母图

命题2设G′为G的度能被3整除的生成母图，则G到G′需增加的度和为偶数.

证明由定理1知任意图G所有顶点的度和为偶数，G′所有顶点的度和也为偶数，所以是偶数，故命题成立.

定理2设G为简单图，如果|V(G)|=3k+1(k=1,2,···)，则G存在度能被3整除的生成母图.

证明阶为3k+1的简单图其最大度为3k，故只要将每个顶点与其余顶点均相连，所得生成母图每个顶点的度都是3k且为完全图，即为度能被3整除的生成母图.

定理3若|V(G)|=3k(k=1,2,···)，△(G)≤−1，则G存在度能被3整除的生成母图.

证明设G是G的补图，由△(G)≤−1，得由Dirac’s定理，G中有Hamilton圈C.将G加边至完全图Kn，设v ∈V(Kn)，则=3k−1，则Kn−C，即为G的度能被3整除的生成母图.

定理4设|V(G)|=3k+2，且k为偶数.若G有完美匹配M，则G存在度能被3整除的生成母图.

证明将G加边至完全图Kn，设v ∈V(Kn)，则dKn(v)=3k+1，则Kn−M为G的度能被3整除的生成母图.

1.2 特殊图类度能被3整除的生成母图的构造

具有n个顶点的路为Pn，记Pn=v1v2···vn.称二部图K1,n−1是n阶星图，记为Sn，Sn中与其余顶点都相邻的点称为中心点，记为s.将n阶星图Sn的1度顶点连成圈，所得图称为n阶轮图，记为Wn.两个星图的中心点用一条边相连，所得的图称为双星图Sm,n，两个中心点分别记为s1,s2，与s1相邻的点记为ui(i=1,2,···,m)，与s2相邻的点记为vi(i=1,2,···,n).下面给出了路图、星图和双星图度能被3整除的生成母图的完全刻画.

定理5对于路Pn，当n=4或n ≥6时Pn存在度能被3整除的生成母图；当n=5时Pn没有度能被3整除的生成母图.

证明设路Pn=v1v2···vn，其度能被3整除的生成母图记为，下面按Pn的阶数分类讨论.

情形1当n=4时，由定理2知Pn存在度能被3整除的生成母图K4，且K4是P4的最优母图.

情形2当n=5时，若P5存在度能被3整除的生成母图，而≤4，则中所有顶点的度只能为3，此时需为两端点各加2度，中间3个顶点各加1度，共增加7度，由命题1知P5没有度能被3整除的生成母图.

情形3.1当n ≥6时且n为偶数时，将Pn加边使其有度能被3整除的生成母图，先考虑将两端点各增加2度，其余顶点各增加1度，共增加n+2度，由命题1知可能存在度能被3整除的生成母图，下证其存在性.由n ≥6，v1与v2是不同的两顶点，与vn是不同的两顶点，加边则每个顶点都只需1度即可被3整除，n是偶数，增加边集E1={vivj|i+j=n+1}，生成母图的边集=E(Pn)∪E1，所得生成母图是3正则图，见图1(左)，故路Pn在n ≥6时且n为偶数时存在度能被3整除.

情形3.2当n ≥6时且n为奇数时，将Pn加边使其有度能被3整除的生成母图，先考虑将两端点各增加2度，其余顶点各增加1度，共增加n+2度，由命题1知不存在度能被3整除的生成母图，所以在此基础上给一个顶点再增加3度，即将一个顶点加边至6度，此时需增加n+5度，由命题1知Pn可能存在度能被3整除的生成母图，下证其存在性.不妨设6度顶点为，Pn加边由n ≥6，增加的边不是重边.边集E2={v1vn∪vivj|i+j=n+1}，生成母图的边集为=E(Pn)∪E2，所得生成母图除点外均为3度点，见图1(右)，故路Pn在n ≥6时且n为奇数时存在度能被3整除.

图1 情形3.1、3.2图示Fig 1 Figures of subcases 3.1 and 3.2

现已证明路图Pn在当n=4或n ≥6时Pn存在度能被3整除的生成母图，下面构造出增加边数最少生成的度能被3整除的生成母图，即最优母图.对于路图，若将所有顶点加边至3度时存在生成母图，则该母图就是最优母图；若将所有顶点加边至3度时不存在生成母图，考虑将其中一个顶点加边至6度，其余顶点仍加边至3度时是否存在生成母图，以此类推构造路图的最优母图.

推论1定理5的证明中构造出的母图是最优母图.

证明将Pn加边使其有度能被3整除的生成母图且增加的边数最少，即每个顶点增加最少的度，只要将每个顶点的度都增加至[d(v)]3，如果存在每个顶点的度为[d(v)]3的生成母图，则为最优母图.当增加的度和为奇数时由命题1知不存在最优母图，在此基础上给任一顶点再增加3度由命题1知可能存在最优母图，其存在性证明同定理5；当增加的度和为偶数时由定理1知可能存在最优母图，其存在性证明同定理5.

定理6星图Sn，当n=3k+1(k=1,2,···)时，存在度能被3整除的生成母图；当n=3k+2或n=3k (k=1,2,···)时不存在度能被3整除的生成母图.

证明在星图Sn中，d(s)=n−1.当n=3k+1(k=1,2,···)时，由定理1知存在度能被3整除的生成母图且是完全图Kn.

当n=3k+2或n=3k(k=1,2,···)时，有d(s)=3k+1或d(s)=3k−1，不能被3整除，且s已与其余所有的点相连，所以d(s)不能加边至[d(v)]3度，故Sn不存在度能被3整除的生成母图.

推论2星图Sn，当n=3k+1(k=1,2,···)时的最优母图为Wn.

证明当n=3k+1 (k=1,2,···)时，d(s)=3k.由定理1知存在度能被3整除的生成母图且是完全图Kn.但Kn不是Sn的最优母图，中心点s的度已能被3整除，其余点均为2度，只要将1度顶点连成圈，所得的生成母图是轮图Wn的度能被3整除且是最优母图.

定理7双星图Sm,n存在度能被3整除的生成母图.

证明对于双星图Sm,n，我们分以下7种情况讨论：

情形1当m=2，n=2时，显然有度能被3整除的生成母图且是3正则图.当m=2，n=3时，d(s2)=4，设v是Sm,n的生成母图的顶点，则maxd(v)=6，为得到S2,3的度能被3整除的生成母图，S1已满足要求，S2必须加相联的边至6度，且只能与u1和u2分别相连，再将u1和u2相连，v1,v2,v3连成圈，所得生成母图的度能被3整除.

情形2当m=3k1,n=3k2(k1,k2=1,2,···)时，有d(s1)=3k1+1，d(s2)=3k2+1，设v ∈Sm,n，将v加边至[d(v)]3度，所有的顶点都只需2度，其度即可被3整除，需增加的度和为6k1+6k2+4，由命题1知Sm,n可能存在度能被3整除的生成母图，下证其存在性.s1只能与N={vi|i=1,2,···,n}中的任意两个顶点相连，不妨设为v1和vn，s2只能与M={ui|i=1,2,···,m}中的任意两个顶点相连，不妨设为u1和um，再将u1,u2,···,um和v1,v2,···,vn分别连成路，所得的生成母图就是度能被3整除的生成母图.

情形3当m=3k1,n=3k2+1(k1,k2=1,2,···)时，d(s1)=3k1+1，d(s2)=3k2+1，设v ∈Sm,n，将v加边至[d(v)]3度，需增加6k1+6k2+5度，由命题1知不存在度能被3整除的生成母图，现考虑在此基础上将其中任意一个顶点再增加3度，此时需增加6k1+6k2+8度，由命题1知可能存在度能被3整除的生成母图，下证其存在性.s1只能与N={vi|i=1,2,···,n}中的任意两个顶点相连，不妨设为v1和vn，s2只能与M={ui|i=1,2,···,m}中的任一顶点相连，不妨设为u1，经验证再增加3度的顶点的选取不影响构造满足要求的生成母图，不妨将顶点v1增加至6度，将v1与u1,u2,um,v1分别相连，将u2,u3,···,um和v1,v2,···,vn分别连成路，所得的生成母图就是度能被3整除的生成母图.

情形4当m=3k1,n=3k2+2(k1,k2=1,2,···)时，d(s1)=3k1+1，d(s2)=3k2+3，设v ∈Sm,n，将v加边至[d(v)]3度，s2已满足要求，其余所有的顶点均只需2度其度即可被3整除，需增加的度和为6k1+6k2+6，由命题1知Sm,n可能存在度能被3整除的生成母图，下证其存在性.s1只能与N={vi|i=1,2,···,n}中的任意两顶点相连，不妨设为v1和vn，将u1,u2,u3,···,um连成圈，将v1,v2,···,vn连成路，所得的生成母图就是度能被3整除的生成母图.

图2从左到右分别表示当m=3k1,n=3k2；m=3k1,n=3k2+1；m=3k1,n=3k2+2时Sm,n的度能被3整除的生成母图的一种情况.

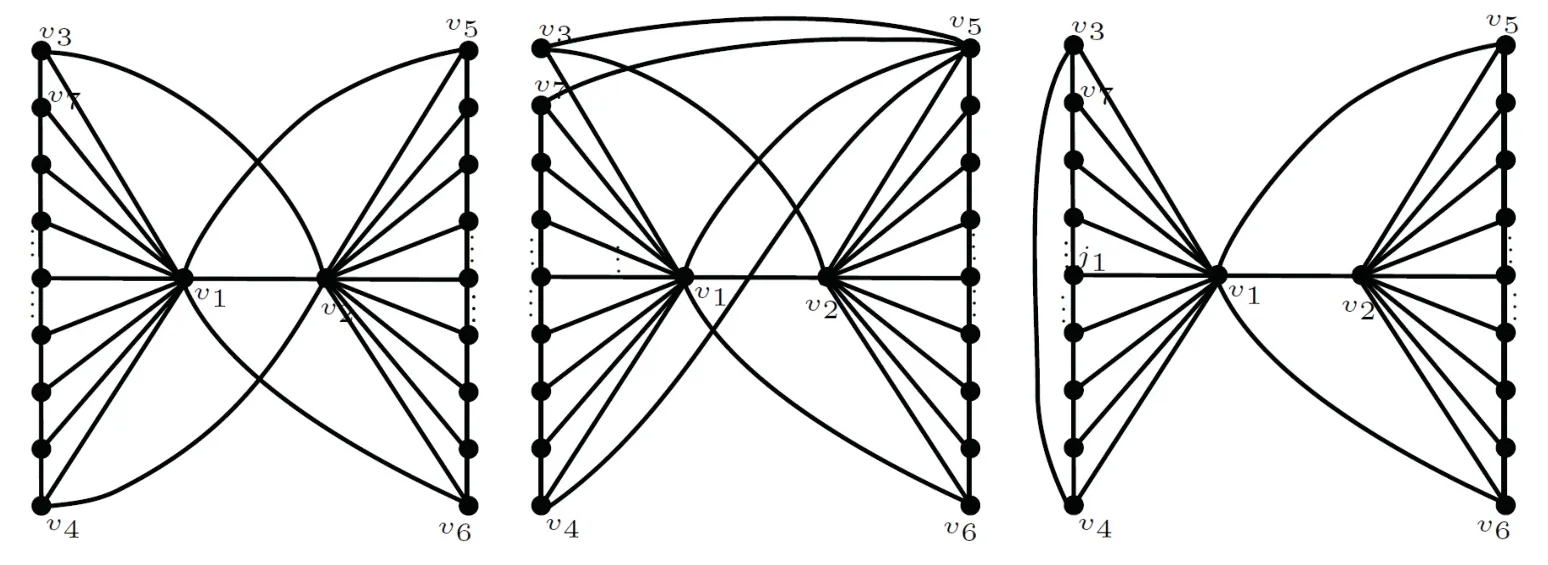
图2 情形2、3和4的图示Fig 2 Figures of subcases 2,3 and 4

情形5m=3k1+1,n=3k2+1(k1,k2=1,2,···)时，d(s1)=3k1+2，d(s2)=3k2+2，设v ∈Sm,n，将v加边至[d(v)]3度，s1和s2需增加1度，其余所有的顶点均需2度即可被3整除，需增加的度和为6k1+6k2+6，由命题1知Sm,n可能存在度能被3整除的生成母图，下证其存在性.s1只能与N={vi|i=1,2,···,n}中的任一顶点相连，不妨设为v1，s2只能与M={ui|i=1,2,···,m}中的任一顶点相连，不妨设为u1，连接um和vn，将u1,u2,u3,···,um连成路，将v1,v2,···,vn连成路，所得的生成母图就是度能被3整除的生成母图.

情形6m=3k1+1,n=3k2+2 (k1,k2=1,2,···)时，d(s1)=3k1+2，d(s2)=3k2+3，设v ∈Sm,n，将v加边至[d(v)]3度，需增加6k1+6k2+7度，由命题1知不存在度能被3整除的生成母图，现考虑在此基础上将其中任意一个顶点再增加3度，此时需增加6k1+6k2+10度，由命题1知可能存在度能被3整除的生成母图，下证其存在性.s1只能与N={vi|i=1,2,···,n}中的任一顶点相连，不妨设为v1，s2已满足要求，经验证再增加3度的顶点的选取不影响构造满足要求的生成母图，不妨将顶点v1增加至6度，将v1与u1,u2,um,v2分别相连，将u1,u2,u3,···,um和v1,v2,···,vn分别连成路，所得的生成母图就是度能被3整除的生成母图.

情形7m=3k1+2,n=3k2+2(k1,k2=1,2,···)时，d(s1)=3k1+3，d(s2)=3k2+3，设v ∈Sm,n，将v加边至v ∈[d(v)]3度，s1和s2已满足要求，其余所有的顶点均需2度即可被3整除，需增加的度和为6k1+6k2+8，由命题1知Sm,n可能存在度能被3整除的生成母图，下证其存在性.将u1,u2,u3,···,um连成圈，v1,v2,···,vn连成圈，所得的生成母图就是度能被3整除的生成母图.

图3从左到右依次是当m=3k1+1,n=3k2+1；m=3k1+1,n=3k2+2 和m=3k1+2,n=3k2+2时Sm,n的度能被3整除的生成母图的一种情况.

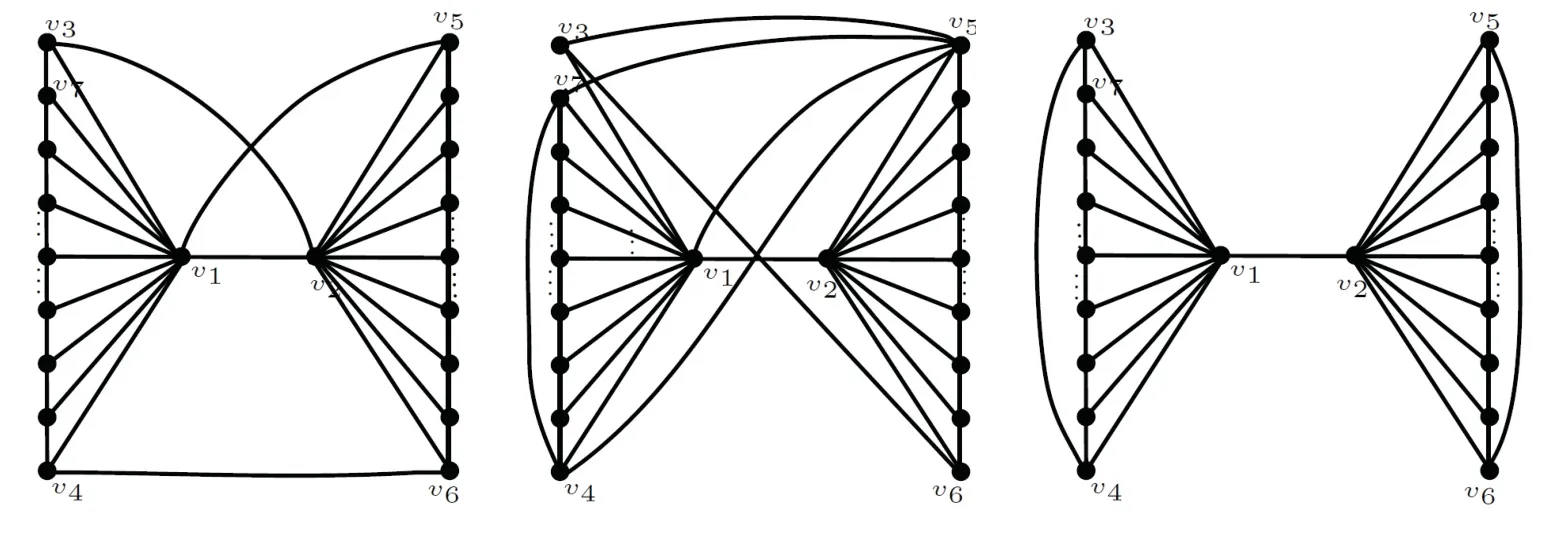
图3 情形5、6和7的图示Fig 3 Figures of subcases 5,6 and 7

1.3 树图度能被3整除的生成母图

命题3设T为树图，∀S ⊆V，ω(−S)≤2.

证明反证，假设ω(−S)≥3，设C1,C2,C3为−S的3个连通分支，则分别在C1,C2,C3中任取一点v1,v2,v3，由于在中v1,v2,v3之间无边，因此在T中，v1v2v3形成一个3圈，与树无圈矛盾，故ω(−S)≤2.

命题4若树图T不是星，则

证明反证，设有两个连通分支C1,C2，若|C1|≥2,|C2|≥2，则在T中C1,C2中的点构成一个长度大于等于4的圈，矛盾.故|C1|=1或|C2|=1，则T是星，矛盾.

定理8树图T不为星图，树图T的顶点数n=3k+2，且n为偶数，则T有度能被3整除的生成母图.

证明由定理4，只需证T有完美匹配.由Tutte’s定理，只需证下证|S|，∀S ⊆V.

情形1S=∅，由于T不是星图，由命题4知，=1.由n为偶数，=0，故

情形2|S|=1，由命题3知，≤2，由于n是偶数，故≤1.

情形3|S|≥2，由命题3知，

故树T不为星图，树T的顶点数n=3k+2，且n为偶数时，T有度能被3整除的生成母图.

2 结论

树图Tn，由定理2知，当n=3k+1时存在度能被3整除的生成母图；由定理8知，当树Tn不为星图，顶点数n=3k+2，且n为偶数时，T有度能被3整除的生成母图；由定理3知，当n=3k且△(T)≤−1时存在度能被3整除的生成母图.对于顶点数n=3k+2，且n为奇数的情况尚未讨论，推测同样存在.