Cyclic Edge-Connectivity and Cyclic Arc-Connectivity of Graphs∗
ZHU Hongzhou,MENG Jixiang
(School of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
Abstract:Let G be a simple graph.The cyclic edge-connectivity cλ(G)is defined to be the minimum cardinality of a subset F of E(G),where G −F is disconnected and has at least two components containing cycles.Let D be a digraph.The cyclic arc-connectivity λc(D) is defined to be the minimum cardinality of a subset S of A(D),where D −S is not strongly connected and has at least two strong components containing directed cycles.In this paper,we establish the cyclic edge-connectivity of the undirected binary Kautz graphs,the undirected de Bruijn graphs and the undirected binary generalized de Bruijn graphs.Moreover,we obtain the cyclic arc-connectivity of the Kautz digraphs,the de Bruijn digraphs and the generalized de Bruijn digraphs.
Key words:cyclic edge-connectivity;cyclic arc-connectivity;de Bruijn graph;Kautz graph;generalized de Bruijn graph
0 Introduction
LetG=(V(G),E(G)) be a simple graph,Fbe a set of edges inG.IfG−Fis disconnected and has at least two components containing cycles,thenFis acyclic edge-cutofG.Clearly,Ghas cyclic edge-cuts if and only if it has two separating cycles.IfGhas a cyclic edge-cut,then it is said to becyclically separable.For a cyclically separable graphG,thecyclic edge-connectivity cλ(G) is defined to be the minimum cardinality of all cyclic edge-cuts[1].IfGis not cyclically separable,then definecλ(G)=∞.
For a digraphD,Discyclically separableifDcontains two vertex disjoint directed cycles.LetDbe a cyclically separable digraph,S⊆A(D).IfD−Shas at least two strong components containing directed cycles,thenSis acyclic arc-cut.For a cyclically separable digraphD,thecyclic arc-connectivityλc(D)is defined to be the minimum cardinality of all cyclic arc-cuts[2].IfDis not cyclically separable,then define λc(D)=∞.The concept of cyclic connectivity dates to the famous incorrect conjecture of Tait in 1880[3]which claimed that every 3-connected cubic planar graph is hamiltonian and thus proved the four color conjecture.Since then,the cyclic connectivity is used in many classic fields of graph theory such as planar graphs[4],integer flow conjectures[5],etc.Recently,Zhang and Zhu[2]studied λc(D1×D2),whereD1andD2are strongly connected digraphs,and λc(Cn1×Cn2×···×Cnk),whereCniis a directed cycle of lengthni(1 ≤i≤k).Wang and Zhang[6]proved an upper bound of the cyclic edge-connectivity of any cyclically separable graph.More results about the cyclic connectivity can also be found in[7-9].
In this paper,we will study the cyclic edge (arc)-connectivities of the Kautz graphs (digraphs),the de Bruijn graphs(digraphs)and the generalized de Bruijn graphs(digraphs).
1 Preliminaries
Given positive integersnandd.TheKautz digraph[10],denoted byK(d,n) (d≥1,n≥1),where every vertexxinV(K(d,n))can be labeled byx1x2···xnsuch thatxi∈{0,1,···,d}fori∈{1,2,···,n},xi+1≠xifori∈{1,2,···,n−1},and for every two verticesx,y∈V(K(d,n)),x1x2···xndominatesy1y2···ynif and only ifxi+1=yifori∈{1,2,···,n−1}.Clearly,K(d,1)is the complete digraph of order(d+1).The Kautz digraphK(2,2)is shown in Fig 1.
The undirected Kautz graphUK(d,n)[11]is obtained fromK(d,n)by deleting the orientation of all arcs and keeping one edge of a pair of multiple edges.Whend=2,the undirected Kautz graphUK(2,n)is called undirected binary Kautz graph.The undirected Kautz graphUK(2,2)is shown in Fig 2.Ford≥2,n≥2,UK(d,n)has the minimum degree 2d−1.Clearly,|V(UK(d,n))|=dn+dn−1.A pair of arcs inK(d,n) is said to be symmetric if they have the same end vertices but different orientations.If(x,y)and(y,x)are a pair of symmetric arcs,we also call one of them a symmetric arc for convenience.An edge inUK(d,n)is said to besingularif it corresponds to a pair of symmetric arcs inK(d,n).It is easy to see that there aresingular edges inUK(d,n).More results about the Kautz digraph and the undirected Kautz graph can also be found in[10-12].

Fig 1 The Kautz digraph K(2,2)
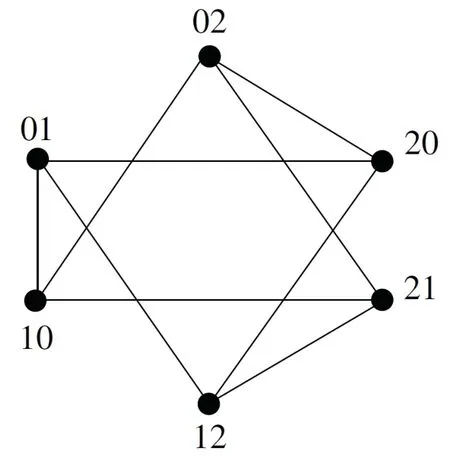
Fig 2 The undirected Kautz graph UK(2,2)
The de Bruijn digraph[10],denoted byB(d,n)(d≥2,n≥2),where every vertexxinV(B(d,n))can be labeled byx1x2···xnsuch thatxi∈{0,1,···,d−1},fori∈{1,2,···,n},and for every two verticesx,y∈V(B(d,n)),x1x2···xndominatesy1y2···ynif and only ifxi+1=yifori∈{1,2,···,n−1}.The de Bruijn digraphB(2,2)is shown in Fig 3.The undirected de Bruijn graphUB(d,n)[13]is obtained fromB(d,n)by deleting loops,the orientation of all arcs and keeping one edge of a pair of multiple edges.Clearly,forn≥2 the Kautz digraphK(d,n)is obtained fromB(d+1,n)by deletion of all vertices of the formx1x2···xnsuch thatxi=xi+1for somei.The undirected de Bruijn graphUB(2,2)is shown in Fig 4.More results about the de Bruijn digraph and the undirected de Bruijn graph can also be found in[10,13,14].
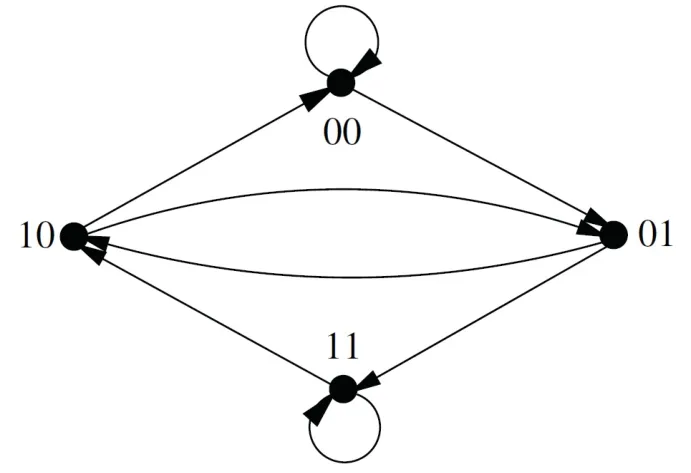
Fig 3 The de Bruijn digraph B(2,2)
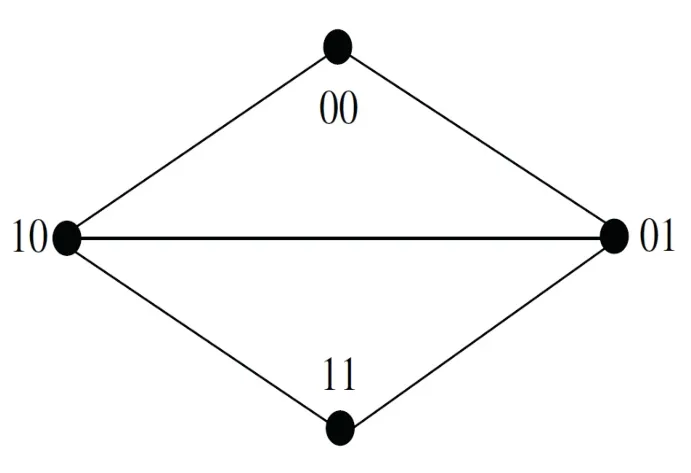
Fig 4 The undirected de Bruijn graph UB(2,2)
The generalized de Bruijn digraphBG(d,n)(d Fig 5 The generalized de Bruijn digraph BG(2,5) Fig 6 The undirected generalized de Bruijn graph UBG(2,5) For terminology and notation not mentioned here we follow[17].LetDbe a digraph.For a vertexxand a vertex setHofV(D),denoteA+(x)={(x,y)∈A(D)|y∈V(D)}andA+(H)={(x,y)∈A(D)|x∈H,y∈V(D−H)}.LetGbe a graph.For a vertexxand a subsetHofV(G),denoteS(x)={xy|yis a neighbor ofx}andS(H)={xy|x∈H,y∈V(G)H}.For two subsetV1andV2ofV(D),denoteA(V1,V2)={(x,y)|x∈V1,y∈V2}. Ak−restricted edge cut of a connected graphGis an edge cut that disconnects the graph without any component having order less thank.Thek−restricted edge connectivity λk(G)[18−19]of a graph G is the minimum cardinality over allk−restricted edge cuts ofG.Let[A,B]indicate the set of edges with one end vertex inAand the other inB.Denote byGAthe graph obtained by removing all the vertices ofAfromG.Define ϕ(A)=|[A,GA]| and ξm(G)=min{ϕ(X) :Xis a connected vertex-induced subgraph of ordermof graphG}.It is known that λ3(G)≤ξ3(G)[12].GraphGis called maximal 3-restricted edge connected[20]if λ3(G)=ξ3(G). Lemma 1[20]The undirected Kautz graphUK(2,n)is maximal 3-restricted edge connected whenn≥3(i.e.λ3(UK(2,n))=ξ3(UK(2,n))). Lemma 2[20]Letn≥4,then ξ3(UK(2,n))=6. Lemma 3Letn≥3,then ξ3(UK(2,n))=6. ProofLetFbe a connected subgraph ofUK(2,n) of order three.IfFis aC3ofUK(2,n).ThenE(F) contains no singular edge and |S(V(F))|=6.IfFis a path of length 2 ofUK(2,n) such thatE(F) contains a singular edge.Then|S(V(F))|=6.IfFis a path of length 2 ofUK(2,n)such thatE(F)contains no singular edge.Then|S(V(F))|=8.By the definition of ξ3(UK(2,n)),we have ξ3(UK(2,n))=6. Lemma 4[15]The undirected generalized de Bruijn graphUBG(2,n)is maximal 3-restricted edge connected whenn≥7(i.e.λ3(UBG(2,n))=ξ3(UBG(2,n))=4). Lemma 5LetK(d,n)be the Kauzt digraph,(x,y)be a symmetric arc inK(d,n)and(x′,x),(y,y′)∈A(K(d,n)).Then(x′,y′)∈A(K(d,n)). ProofLetx=x1x2x1x2···,y=x2x1x2x1···,thenx′=αx1x2x1··· (α ∈{0,1,2,···,d}{x1,x2}),y′=x1x2x1···β (β ∈{0,1,2,···,d}{x1,x2}).Then(x′,y′)∈A(K(d,n)). Lemma 6[21]Ford≥2,n≥2,let(x,y)and(u,v)be a pair of non-adjacent arcs inK(d,n).If(x,y)is a symmetric arc,then there exist 2d−2 internally vertex-disjoint directed paths from{x,y}to{u,v}. Lemma 7[10]B(d,n) is (d−1)-strongly connected,that is,for every pairx≠yof vertices there existd−1 internally vertex-disjoint(x,y)-paths. Lemma 8[10]BG(d,n)is(d−1)-strongly connected,that is,for every pairx≠yof vertices there existd−1 internally vertex-disjoint(x,y)-paths. Lemma 9cλ(UK(d,n))≤6d−6 ford≥2,n≥3. ProofClearly,cλ(UK(2,2))=3.Letx,y,z∈V(UK(d,n)),x=x1x2x3x1x2x3···,y=x2x3x1x2x3x1···,z=x3x1x2x3x1x2···,wherex1≠x2≠x3.Thenxyzis aC3inUK(d,n).Clearly,|S({x,y,z})|=6d−6.Letx′=x3x2x1x3x2x1···,y′=x2x1x3x2x1x3···,z′=x1x3x2x1x3x2···.Thenx′y′z′is aC3inUK(d,n)−{x,y,z} andS({x,y,z}) is a cyclic edge-cut ofUK(d,n).Hence,cλ(UK(d,n))≤6d−6. Lemma 10cλ(UK(2,n))≥6 forn≥3. ProofSuppose that there is a minimum cyclic edge-cutFsuch that|F|≤5,and the deletion ofFdisconnectsUK(2,n).Thus,UK(2,n)−Fhas two components containing cycles.By Lemmas 1 and 3,λ3(UK(2,n))=ξ3(UK(2,n))=6.Since|F|<6=λ3(UK(2,n)),one component ofUK(2,n)−Fhas at most 2 vertices,which is a contradiction. By Lemmas 9 and 10,we deduce the following result. Theorem 1cλ(UK(2,n))=6 forn≥3. Theorem 2cλ(UB(d,n))≤6d−6 ford≥3,n≥3. ProofSimilar to the proof of Lemma 9,we can show thatcλ(UB(d,n))≤6d−6. Lemma 11cλ(UBG(2,n))≤4 ifnis even withn≥8. ProofSince both the vertex subsetsand−1,n−2,n−1}inV(UBG(2,n))can induce a triangleC3,where 0 is ordinary vertex.Clearly,S({0,1,is a cyclic edge-cut ofUBG(2,n)andcλ(UBG(2,n))≤|S({0,1,=4. Lemma 12Letn∈{7,9},thencλ(UBG(2,n))≤4. ProofForn=7.Since both the vertex subsets{1,2,4}and{3,5,6}inV(UBG(2,n))can induce a triangleC3,where 2 and 4 are alternating vertices.Clearly,S({1,2,4})is a cyclic edge-cut ofUBG(2,n)andcλ(UBG(2,n))≤|S({1,2,4})|=4. Forn=9.Since both the vertex subsets{1,2,5}and{3,6,7}inV(UBG(2,n))can induce a triangleC3,where 2 and 5 are alternating vertices.Clearly,S({1,2,5})is a cyclic edge-cut ofUBG(2,n)andcλ(UBG(2,n))≤|S({1,2,5})|=4. Lemma 13cλ(UBG(2,n))≤6 ifnis odd withn≥11. ProofSince both the vertex subsets {1,2,+1} and−1,n−3,n−2} inV(UBG(2,n)) can induce a triangleC3,S({1,2,+1})is a cyclic edge-cut ofUBG(2,n)andcλ(UBG(2,n))≤|S({1,2,+1})|=6. Lemma 14cλ(UBG(2,n))≥4 ifn≥7. ProofSuppose that there is a minimum cyclic edge-cutFsuch that|F|≤3,and the deletion ofFdisconnectsUBG(2,n).Thus,UBG(2,n)−Fhas two components containing cycles.By Lemma 4,λ3(UBG(2,n))=ξ3(UBG(2,n))=4.Since|F|<4=λ3(UBG(2,n)),one component ofUBG(2,n)−Fhas at most 2 vertices,which is a contradiction. By Lemmas 11,12,13 and 14,we deduce the following result. Theorem 3LetUBG(2,n)be the undirected binary generalized de Bruijn graph,then (1)cλ(UBG(2,n))=4 ifnis even withn≥8; (2)cλ(UBG(2,n))=4 ifn∈{7,9}; (3)4 ≤cλ(UBG(2,n))≤6 ifnis odd withn≥11. Lemma 15 ProofSinceK(2,1) is the complete digraph of order 3,it is not cyclically separable.Whend≥3,K(d,1) is the complete digraph of orderd+1.Letu,v∈V(K(d,1)).Clearly,A+({u,v})is a cyclic arc-cut ofK(d,1).Then λc(K(d,1))≤2d−2.LetSbe a minimum cyclic arc-cut ofK(d,1).SinceK(d,1)−Shas two strong componentsD1andD2containing directed cycles,|D1|≥2 and|D2|≥2.This implies that|S|≥2d−2 and λc(K(d,1))=|S|≥2d−2.Thus,λc(K(d,1))=2d−2. Lemma 16λc(K(d,n))≤2d−2 ford≥2,n≥2. ProofLet(x,y)be a symmetric arc inD=K(d,n)(d≥2,n≥2).LetD1=D[{x,y}],D2=D−D1.Foru,v∈V(D2),we consider two cases. Case 1d=2.Since κ(D)=d=2,there are two internally vertex-disjoint(u,v)−pathsP1andP2inD.If one ofP1andP2contains neitherxnory,then there is a(u,v)−path inD2.If|V(Pi)∩{x,y}|≠∅,i∈{1,2}.In this case we setx∈V(P1),y∈V(P2),and let(w,x)∈A(P1),(y,z)∈A(P2).By Lemma 5,(w,z)∈A(D).Note thatP1contains a(u,w)-path andP2contains a(z,v)-path.Thus there is a(u,v)-path inD2.Similarly,there is a(v,u)−path inD2.It follows thatD2is a strong component ofD. Case 2d≥3.Since κ(D)=d≥3,then there aredinternally vertex-disjoint(u,v)−paths inD.Thus,there is(u,v)−path inD2.Similarly,there is a(v,u)−path inD2.It follows thatD2is a strong component ofD. Clearly,D2contains a directed cycle.ThereforeA+({x,y})=2d−2 is a cyclic arc-cut inD.Thus,λc(K(d,n))≤2d−2 ford≥2,n≥2. Lemma 17λc(K(d,n))≥2d−2 ford≥2,n≥2. ProofLetD=K(d,n),S⊆A(D)be a minimum cyclic arc-cut ofD.Then|S|=λc(D).Thus,V(D)is divided into two disjoint subsetsV1andV2andS=A(V1,V2).By the definition ofS,|V1|≥2,|V2|≥2.Since there arepairs of symmetric arcs inDand>2d−2,one ofD[V1]andD[V2]has at least a pair of symmetric arcs.By Lemma 6,|S|≥2d−2.Therefore,λc(D)=|S|≥2d−2. By Lemmas 15,16 and 17,we have the following result. Theorem 4λc(K(d,n))=2d−2 ford≥3,n=1 ord≥2,n≥2. Theorem 5λc(B(d,n))=d−1 ford≥2,n≥2. ProofLetxbe a vertex inB(d,n) such that (x,x) ∈A(B(d,n)).ThenA+({x}) is a cyclic arc-cut inB(d,n).Clearly,λc(B(d,n))≤|A+({x})|=d−1. On the other hand,letS⊆A(B(d,n)) be a minimum cyclic arc-cut ofB(d,n).Then |S|=λc(B(d,n)) andV(B(d,n)) is divided into two disjoint subsetsV1andV2such thatS=A(V1,V2).Since a loop is a directed cycle of length 1,|V1|≥1,|V2|≥1.By Lemma 7,|S|≥d−1 and λc(B(d,n))=|S|≥d−1.Thus,λc(B(d,n))=d−1 ford≥2,n≥2. Theorem 6λc(BG(d,n))=d−1 ford≥2,n≥2. ProofLetxbe an ordinary vertex inBG(d,n).ThenA+({x})is a cyclic arc-cut inBG(d,n)and λc(BG(d,n))≤|A+({x})|=d−1. On the other hand,letS⊆A(BG(d,n))be a minimum cyclic arc-cut ofBG(d,n).Then|S|=λc(BG(d,n))andV(BG(d,n))is divided into two disjoint subsetsV1andV2such thatS=A(V1,V2).Since a loop is a directed cycle of length 1,|V1|≥1,|V2|≥1.By Lemma 8,|S|≥d−1 and λc(BG(d,n))=|S|≥d−1.Thus,λc(BG(d,n))=d−1 ford≥2,n≥2. In this paper,we determinedcλ(UK(2,n))=6 forn≥3;cλ(UB(d,n))≤6d−6 ford≥3,n≥3;cλ(UBG(2,n))=4 ifn∈{7,9}ornis even withn≥8;4 ≤cλ(UBG(2,n))≤6 ifnis odd withn≥11;λc(K(d,n))=2d−2 ford≥3,n=1 ord≥2,n≥2;λc(B(d,n))=d−1 ford≥2,n≥2;λc(BG(d,n))=d−1 ford≥2,n≥2.For future research,one may determine the cyclic vertex-connectivity of the Kautz graphs,the de Bruijn graphs and the generalized de Bruijn graphs,and explore the cyclic edge-connectivity and the cyclic arc-connectivity of other interconnection networks.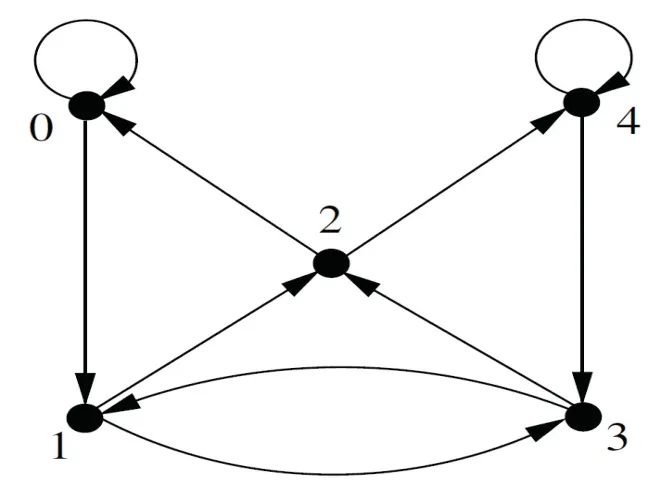

2 Cyclic edge-connectivity of UK(2,n),UB(d,n)and UBG(2,n)
2.1 Cyclic edge-connectivity of UK(2,n)
2.2 Cyclic edge-connectivity of UB(d,n)
2.3 Cyclic edge-connectivity of UBG(2,n)
3 Cyclic arc-connectivity of K(d,n),B(d,n)and BG(d,n)
3.1 Cyclic arc-connectivity of K(d,n)
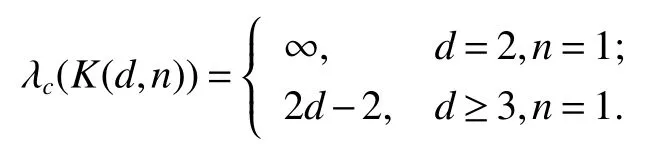
3.2 Cyclic arc-connectivity of B(d,n)
3.3 Cyclic arc-connectivity of BG(d,n)
4 Conclusion

