Event-Based Fixed-Time Bipartite Consensus for Multi-Agent Systems with Time Delay and Interference∗

WEI Xiaojie,JIANG Haijun,YU Zhiyong

(School of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)

Abstract:This article studies the fixed-time bipartite consensus problem of multi-agent systems with time delay and unknown interference.First,a fixed-time event-triggered controller is designed.Then,using algebraic graph theory,fixed-time stability theory and set-valued Lie derivative,we prove that the system can achieve bipartite consensus within a fixed time under the control protocol.In addition,the system will not produce Zeno phenomenon under the proposed event-triggered algorithm.Finally,the validity of the theoretical analysis is verified by two numerical examples.

Key words:multi-agent systems;event-triggered;fixed-time bipartite consensus;time delay

0 Introduction

Multi-agent systems(MASs)is a vital branch of distributed artificial intelligence in recent decades,which can be used to solve complicated realistic problems[1−2].Consensus,as a representative group behavior in MASs[3],means that all agents reach the same state under appropriate control protocols.In practical application,there may be both competitive and cooperative behaviors in the system,such as sports competition among multi-robot teams[4−5],etc.Therefore,bipartite consensus of MASs with antagonistic behaviors was studied in[6].

In the study of consensus,the convergence rate is an important indicator to measure the consensus behavior.Compared with the asymptotic convergence,the fixed-time convergence is more in line with practical applications.Therefore,based on the fixed-time stability theory given in[7]and by designing a continuous controller,the finite-time and fixed-time bipartite consensus for the system is studied in [8].In order to reduce energy consumption in the control process,[9] proposed an event-triggered control method.In [10],the fixed-time consensus of MASs with time delay and external interference is studied by designing event-triggered control algorithms.However,there are few articles on the bipartite consensus of MASs with time delay and interference under the event-triggered control protocol.

The main content of this paper is summarized as follows:(1)Based on the event-triggered control method,a distributed control protocol of MASs with time delay and interference is designed.(2) Using algebraic graph theory and fixed-time stability theory,the correlative criteria of MASs to achieve bipartite consensus are given.(3)In order to avoid the chattering phenomenon caused by the sign function in the control,an event-triggered control protocol with a saturation function is designed,and it is proved that the system will not produce Zeno behavior under the two proposed control protocols.

1 Preliminaries and Problem statement

In this paper,N-dimensional real column vector space andN×Mdimensional real number matrix space are represented byRNandRN×M,respectively.For a real matrixG,whenG>0(orG<0)indicates thatGis a positive(or negative)definite matrix,andGTindicates the transpose of matrixG.sign(·) represents the sign function.‖·‖ refers to the two-norm for a vector or the two-norm for a matrix and|·|refers to the one-norm for a vector or the absolute value for a scalar.

Consider a network includes M agents.The network topology is represented by an undirected signed graph G,G is a triple G={V,E,A},where V={v1,v2,···,vM} is the set of nodes,E ⊆V×V is the edge set and A=[aij] ∈RM×Mis the adjacent matrix.If (vj,vi) ∈E,viandvjare neighbors of each other,thenaij≠0.The neighbor node set ofviis denoted as Ni={j:(vj,vi) ∈E}.Assume that network topology G is undirected and does not contain self-loop,thenaij=aji,aii=0(i,j=1,2,···,M).The degree matrix of nodes is H=diag(h1,h2,···,hM)withhi=Define the form of Laplacian matrix L=[lij]∈RM×Mas L=H −A.The elements of L are

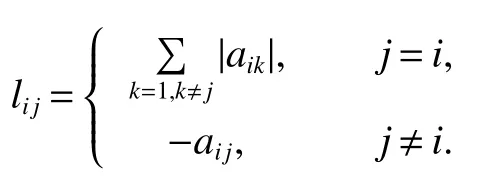
If there is a path fromvitovj,then the undirected signed graph G is said to be connected.Graph G is said to be structurally balanced,if the vertex set V can be divided into subsets V1and V2that satisfy the condition V1∩V2=Ø and V1∪V2=V,and the nodesviandvjin V1(or V2)maintain a coordinate relationship,that is,aij≥0.There are competing relationships in subsets V1and V2,which isaij≤0 for ∀vi∈V1,vj∈V2.Otherwise,the signed graph G is structurally unbalanced.

Lemma 1[6]For the adjacency matrix A ∈RM×Mof structurally balanced signed graph G,there exists a gauge transformation performed byU=diag(σ1,σ2,···,σM)(σi∈{−1,1}),such that all the entries ofUAUare nonnegative.

Remark 1For the problem of the bipartite consensus of MASs,structurally balanced is a condition that the network topology must satisfy.If the signed graph G is structurally unbalanced,MASs will converge to the same state.This result is also verified in the numerical simulation examples.

Lemma 2[6]Denote a new Laplacian matrix LU,The elements of LUare

then L and LUhave same eigenvalues.

Lemma 3[11]For connected and undirected unsigned graph,its corresponding Laplacian matrixsatisfies the following property:

(1)sTwheres=[s1,s2,···,sM]T,

(3)if 1T s=0,one havesT≥λ2sT s.

Remark 2For signed graph G,since the adjacent matrix A has both positive and negative weights,the Laplacian matrix L does not satisfy the row sum to be zero.Therefore,lemma 2 defines a new Laplace matrix LUthat satisfies row sum zero,then the bipartite consensus problem can be transformed into a general consensus problem to solve.

Consider the following dynamics ofi-th agent

wheresi(t),ui(t),τi,ri(t)(i=1,2,···,M)represent the state information,control input,time delay and unknown interference respectively.

Assumption 1Assume that there is a positive constantsuch that

Definition 1For MASs(1),if there is a bounded constantT>0 independent of the initial state of the system,which satisfies−σiσjsj(t)|=0.Whent>T,there issi(t)=σiσjsj(t),then the system(1)reaches bipartite consensus in a fixed time.AndTis called the settling time estimate.

Lemma 4[7]For MASs(1),there exists a continuous radial unbounded functionF(t),which satisfies the inequalities:≤−µFp(s(t))−νFq(s(t)),whereµ,ν>0,p∈(0,1)andq∈(1,∞).Then the system(1)reaches consensus within the fixed settling timeT(s),andT(s)≤Tmax=In addition,if there is a constant ω>0 forF(t),satisfies the inequality:˙F(s(t))≤−µFp(s(t))−νFq(s(t))+ω,the system(1)achieves actually fixed-time consensus.

Lemma 5[12]For constans ξ1,ξ2,···,ξK≥0,one have

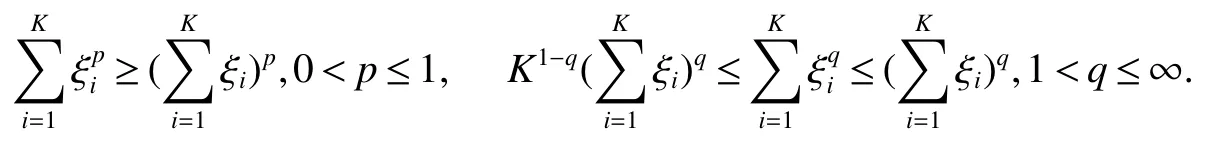
2 Main Results

First,using the event-triggered control method,the control input of thei-th agent is constructed as follows

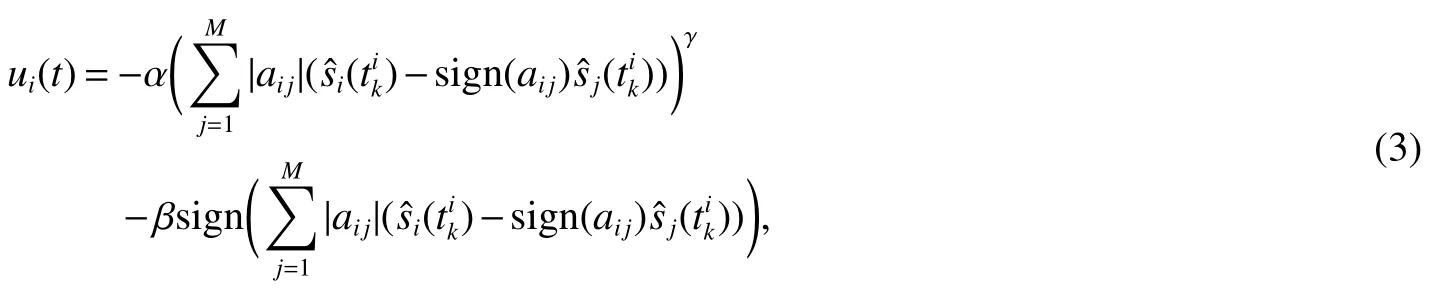
In order to simplify(3),defineyi(t)as

So the event-triggered controller can be simplified as

Define the measurement error as follows

The trigger function of thei-th agent is constructed as

where ξ ∈(0,1).Each trigger point··· of agentiis given by trigger functiongi(t).In other words,whengi(t)≥0,the controller is triggered and updates the state information of agenti,and then transmit the information to its neighbor nodes.During the operation of the controller,the data used are all the latest updated values of the agents.

Theorem 1For MASs(1),the control protocol(6)with trigger function(8)is considered.If assumption 1 is true and network topology G is a structurally balanced and connected signed graph,and control gains α and β satisfy

then MASs(1)can achieve fixed-time bipartite consensus,and the estimate of the settling timeT(s)is

where constantsa>0 andb>0,γ ∈(1,∞).

ProofConstruct a new variable

In view of lemma 2 and lemma 3,the following inequality holds

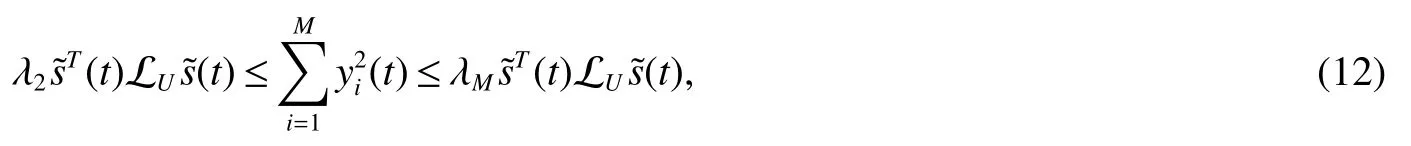
where λ2and λMare the minimum and maximum eigenvalues of LU.

Choose the Lyapunov function asV(t)=Due to the discontinuity of(11),according to the set-valued Lie derivative,the derivative ofV(t)is

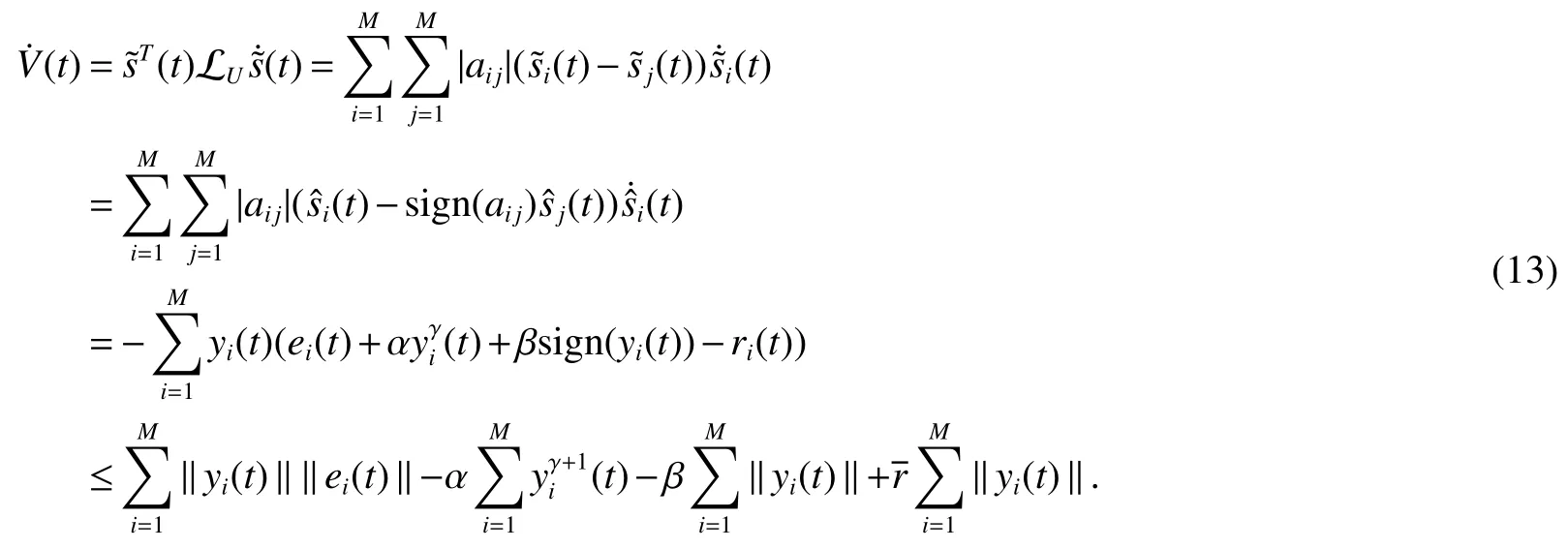
Whent∈according to the trigger condition,‖ei(t) ‖<ξα ‖(t) ‖ +ξβ can be obtained.Combined with the condition(9),we have

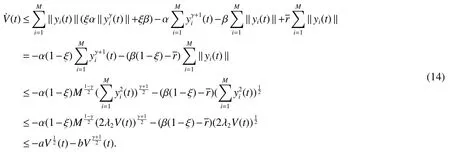
In accordance with lemma 4,we can obtain

And the settling timeTsatisfies the following condition

Remark 3It can be seen from theorem 1 that the settling time under the fixed-time stability theory is independent of the initial value of the system.Compared with[8],the difference in this paper is that the influence of time delay and interference is considered in the dynamics,and the event-triggered control method is adopted to study the fixed-time bipartite consensus of MASs.

Next we demonstrate that the event-triggered controller(3)does not produce Zeno phenomenon.

Theorem 2For MASs(1),if the condition of Theorem 1 are true,then,the event-triggered function(8)can exclude the Zeno behaviour.

ProofFrom(12)we can obtain≤2λMV(t)≤2λMV(0),andV(0)=Then,the upper right derivative ofei(t)is

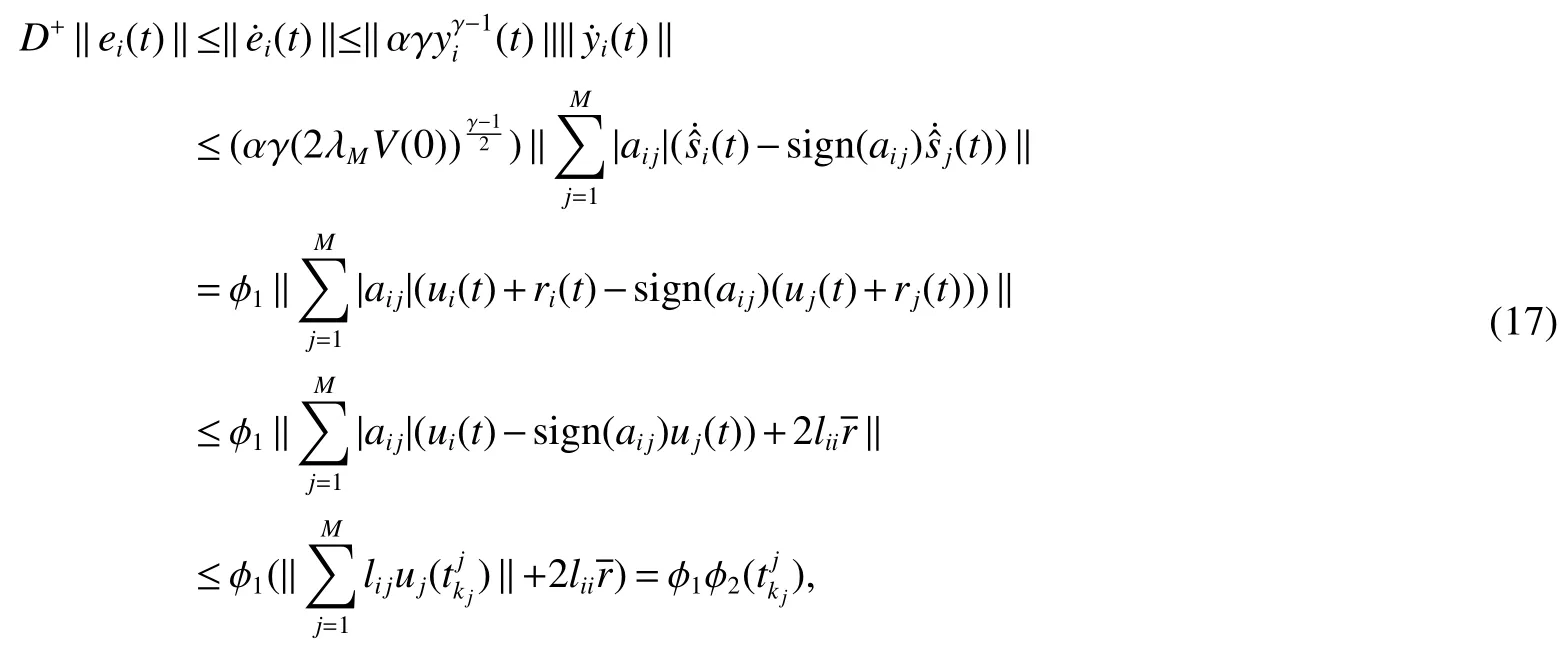
where φ1andare defined as follows

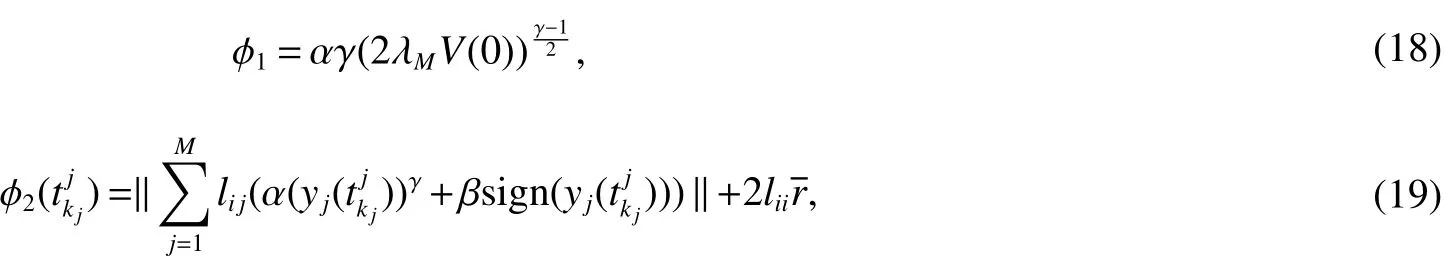
From the trigger conditiongi(t)≥0,one has

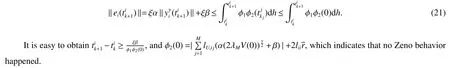
Remark 4The sign function is used in the control protocol (3),when the error tends to zero,the controlui(t) will oscillate.In order to overcome this shortcoming,the saturation function is introduced to improve the controller(6).

Utilizing the saturation function,the controller of thei-th agent is designed as following form

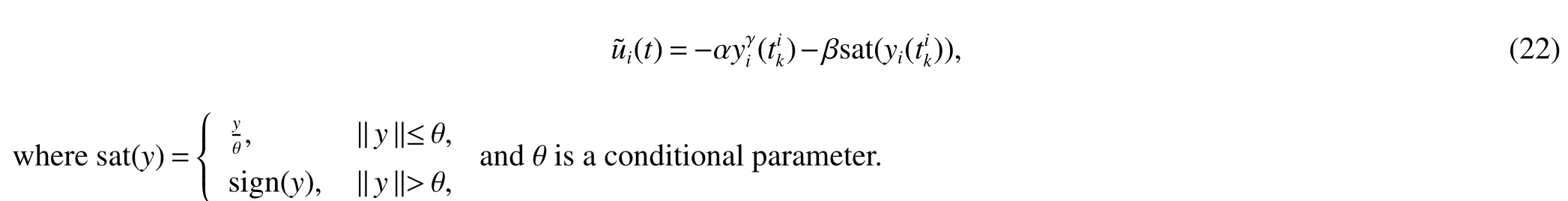
The measurement error and trigger function ofi-th agent are respectively converted into the following forms

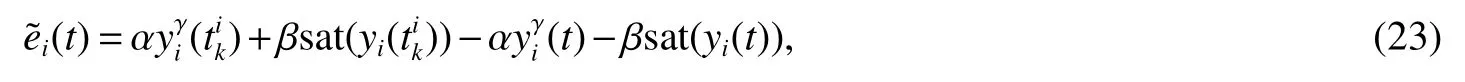
where α,β is control gain,ξ ∈(0,1).the controller of thei-th agent is triggered when

Theorem 3For MASs (1),the control protocol (22) with trigger function (24) is considered.If assumption 1 is true and network topology G is a structurally balanced and connected signed graph,and the gain parameters α and β are the same as theorem 1,then MASs(1)can achieve fixed-time bipartite consensus and avoid Zeno phenomenon.

ProofChoose Lyapunov functionV(t)=whereSimilar to the analysis of Theorem 1 can get

When‖yi(t)‖>σ,the analysis procedure is the same as Theorem 1.When‖yi(t)‖≤θ,sat(yi(t))=we obtain

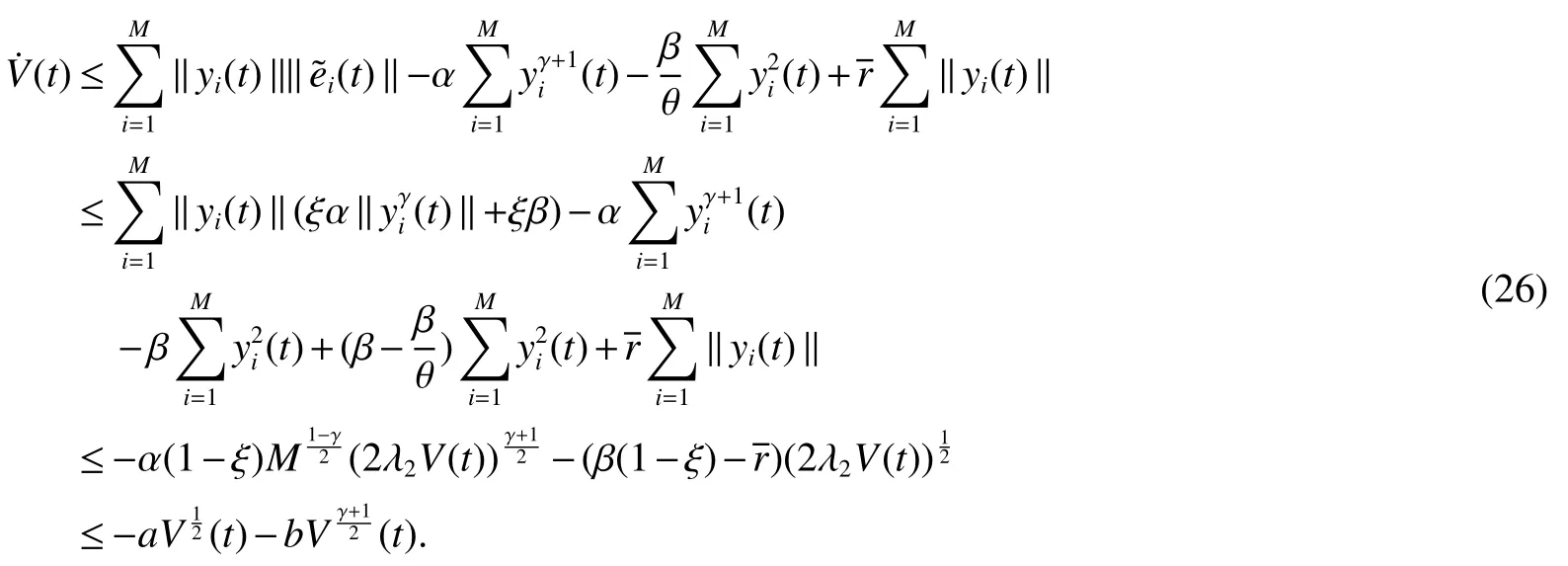
Therefore,similar to the analysis of Theorem 1,the MASs(1)can reach the fixed-time bipartite consensus.

3 Numerical simulations

Consider the MASs (1),which consists of five agents.The structurally balanced and structurally unbalanced network topology is shown in Fig 1 and Fig 2 respectively.In the figure,black lines represent cooperative relationships among agents,and red lines represent competitive relationships.

Fig 1 G1 (structurally balanced)

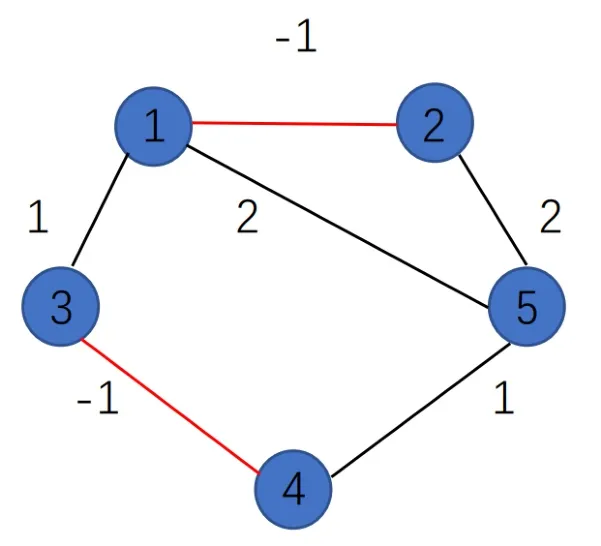
Fig 2 G2 (structurally unbalanced)

In system(1),τi=0.03,ri(t)=0.05cos(t),i=1,2,3,4,5,obviously,the unknown interference satisfies|ri(t)|≤¯r=0.05.The Laplacian matrix of the signed graphs G1is L1,and λ2(L1)=1.491 4 by calculation.In two examples,the fixed-time event-triggered control algorithms of sign function and saturation function are considered respectively.

Example 1(sign function)For MASs(1),the event-triggered control algorithm(6)is considered.Where α=1.138 7,β=0.827 6,γ=ξ=0.6,the condition of Theorem 1 is established through calculation,andTmax=10.The initial conditions of the system are:s1(0)=−2;s2(0)=−4;s3(0)=1;s4(0)=5;s5(0)=1.then the state of MASs(1)is shown in Fig 3.The trigger point of each agent is shown in Fig 4.Obviously,the system can achieve bipartite consensus under the control protocol.

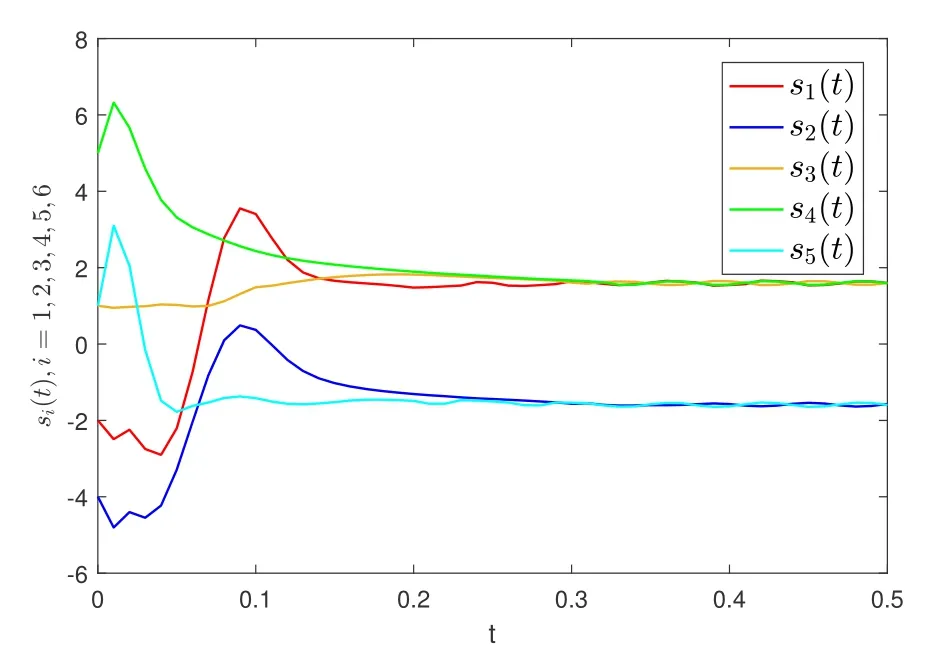
Fig 3 The state of si (i=1,2,3,4,5)

Fig 4 The trigger point under the trigger function(8)

Example 2(saturation function)For MASs(1),the event trigger control algorithm(22)is considered,where θ=0.01 and other parameters are the same as example 1,the condition of Theorem 3 can be verified.The initial conditions of the system are:s1(0)=3;s2(0)=−6;s3(0)=3;s4(0)=2;s5(0)=4.Then the state of MASs(1)is shown in Fig 5.The trigger point of each agent is shown in Fig 6.

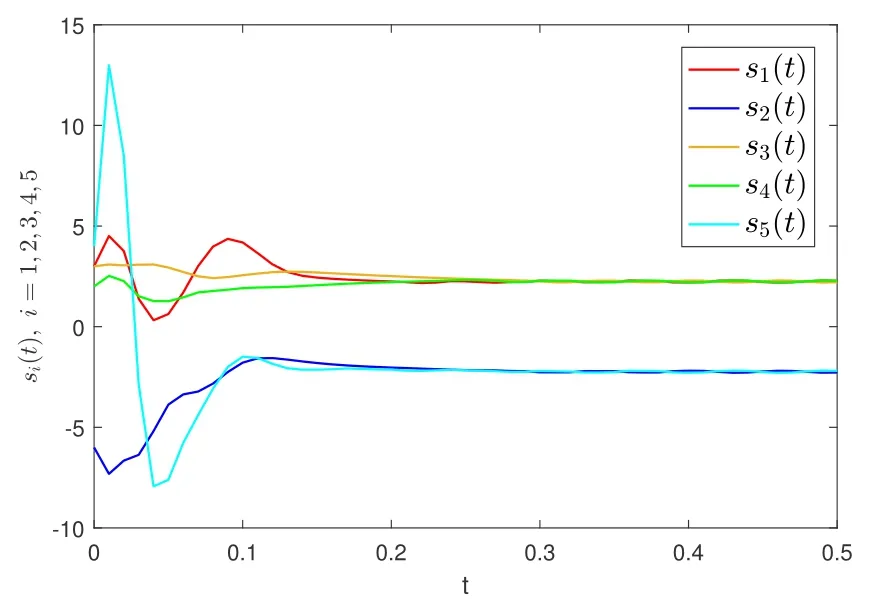
Fig 5 The state of si (i=1,2,3,4,5)

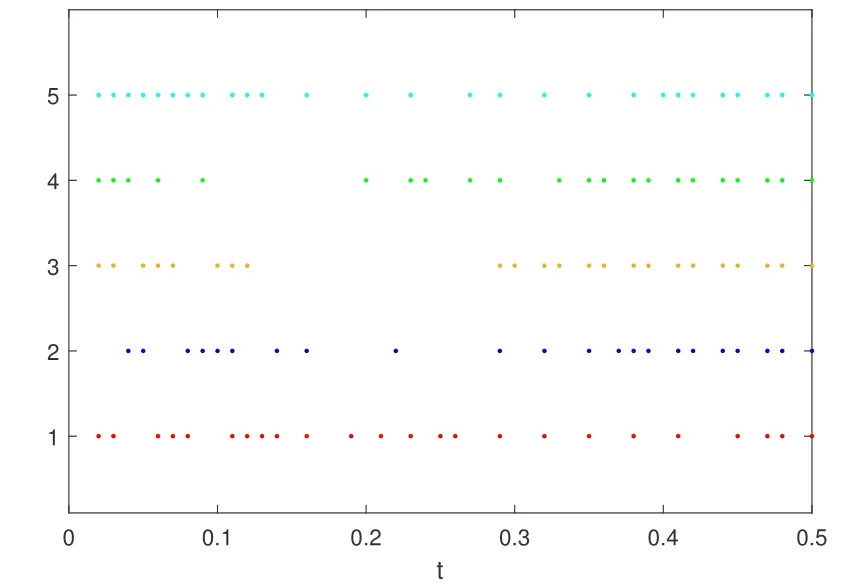
Fig 6 The trigger point under the trigger function(24)

In addition,if the network topology is unbalanced(as shown in Fig 2),under the control protocol(6)and(22),the state of the system is shown in Fig 7 and Fig 8,that is,the state of the agent converges to the same value.

Fig 7 The state of si (i=1,2,3,4,5)under the controller(6)

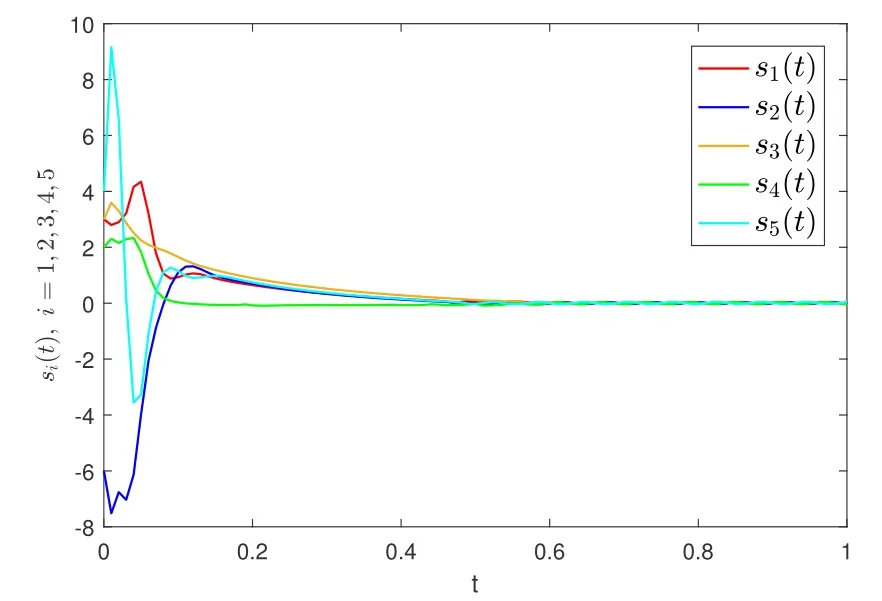
Fig 8 The state of si (i=1,2,3,4,5)under the controller(22)

4 Conclusion

Based on the event-triggered control method,this paper studies the fixed-time bipartite consensus of MASs with time delay and unknown interference.By designing two different control protocols,and using the fixed-time stability theory to give the bipartite consensus criteria for MASs.It is proved Zeno phenomenon will not occur under the control protocols.Finally,two numerical examples are given to verify the feasibility of the protocols.