K型纳米阵列结构的圆二色性研究

荆敏娟

(运城学院 物理与电子工程系，运城 044000)

圆二色性(Circular Dichroism,CD)效应是指手性结构对左旋圆偏振 (Left Circular Polarization,LCP)光和右旋圆偏振(Right Circular Polarization,RCP) 光的吸收差异[1-2]。它是药物检测，超薄玻片及光电子器件设计的关键。然而天然手性分子的CD较弱，阻碍了它在红外的广泛应用，与天然手性分子相比，人工手性贵金属纳米结构将圆二色性提高了几个数量级，并且使得它对入射光的响应扩大到可见、红外波段。手性最早出现在自然结构和分子中，比如人的手跟脚、贝壳、树叶、DNA、氨基酸分子、蛋白质等等。手性作为解开生命起源的途径，一直是研究的热点。然而天然手性分子对入射光的响应及其微弱而且只限于紫外波段，限制了其有效的应用。近几年，兴起的人工金属纳米手性结构与天然手性化合物相比较，它具有更强的手性信号，而且对入射光的响应扩大到可见、红外波段[3-8]。

F.J.D.Arago等学者于 1811 年在石英材料中观测到圆二向色性与圆双折射现象。1997年Arnaut[9]等人最早将平面手性结构引入到电磁学研究中来，采用这种平面结构的手性比较微弱。而2006年Rogacheva等人[10]提出双层手性结构。不同形状手性结构的研究开始层出不穷，近些年研究者们提出多种金属手性纳米结构来探索CD效应产生的物理机制。例如2014年Y.Cai等人[11]设计的矩形裂环通过对称性破缺和倾斜入射光获得CD，金属螺旋结构[12]属于传统的手性结构但CD微弱，二聚体结构[13]虽然能灵活操作和制备,但在近红外的CD响应小于0.1，也有对三维六叶风车[14]、倾斜L型[15]等的研究。在2D人工纳米结构中，如万字符型[16]、X型[17]、S型[18]结构等，这些研究结果指出2D手性结构的CD对结构的形状、几何尺寸、材料以及周围环境很敏感。且因二维手性纳米结构易于制造且应用广泛而引起了研究者的关注。

一般情况下增强的圆二色性响应只能在斜入射时观察到，这不利于其应用。本文设计了二维平面K字型纳米结构阵列，应用有限元方法(Finite Element Method,FEM)计算并分析了其吸收、CD光谱。实验发现，在垂直入射的LCP和RCP条件下，本结构具有增强的圆二色性响应，并产生较大的CD值。这将为设计手性光学器件提供一定的参数指导。

1 结构和仿真方法

图1为在x-y平面上的单元结构示意图，x和y方向的周期分别为Px=500 nm，Py=500 nm。设计了如图2所示的K型结构，其中棒1、棒2、棒3的长度分别为L1、L2、L3，高都为h，宽为w。其中棒2和棒3在棒1上位置可控制，S为棒2和棒3交叉口偏移棒1中心的偏移量。

有限元方法[19-20]的基础是变分原理，其基本求解思想是把计算域划分为有限个不重叠的单元。在每个单元内，选择一些合适的节点作为求解函数的插值点。将微分方程中的变量改写成由各变量或其导数的节点值与所选用的插值函数组成的线性表达式，借助于变分原理或加权余量法，将微分方程离散求解。

图1 单元结构示意图

图2 K型参数示意图Fig.2 K-type parameters

在各向同性介质中，微分形式的Maxwell方程组可表示为

(1)

(2)

(3)

(4)

式(1)表示安培定律；式(2)表示法拉第电磁感应；式(3)表示静电场高斯定律；式(4)表示磁通连续性定理。磁矢势和电矢势由式(1)、式(2)得出，即

(5)

(6)

(7)

ε0、μ0分别表示真空中的介电常数和磁导率；εr、μr为材料的相对介电常数和相对磁导率。

对式(7)进行时域分析，将电磁场表示为时谐波形式如下：

(8)

(9)

联立Maxwell法拉第定律和安培定理并将时间因子消去。

(10)

(11)

式中:ω为角频率；σ为电导率；k0为真空中的波矢。

式(11)主要用于稳态频域问题或者模式分析。处理时，用透射系数和反射系数描述该金属结构光的传输特性。通过能流来计算透射系数和反射系数。电磁波在传播过程中的电能和磁能定义为

(12)

(13)

能量对时间微分，解得电功率、磁功率分别为

(14)

(15)

由式(14)和式(15)可得总功率为

(16)

K型金属纳米结构的透射谱线和非对称传输谱线由商业软件COMSOL Multiphysics计算得到。在计算过程中，其材质设置为金，金的介电函数从Johnson和Christy的实验中获得。

2 数据分析

为构建非固有手性结构，给定了K型结构参数，使得K型纳米结构的几何参数参数为L1=400 nm，L2=200 nm，L3=200 nm，h=40 nm，w=50 nm。图3给出了RCP和LCP光垂直入射情况下S=0，10，20，30，40，50，60，70，80，90 nm的CD光谱，波长范围为600～2 000 nm。S=0是K型纳米结构对称位置，使S以10 nm的长度慢慢偏离对称位置。从图3中可看出在1 400 nm附近它们的波峰和波谷有明显的变化且容易分辨。而且可以发现在1 400 nm附近S=10，20，30，40，50 nm处于波峰，而S=60，70，80，90 nm则处于波谷。从图3中还可发现在1 400 nm附近处的波谷相对波峰发生了红移。为进一步研究，分别列出它们在1 400 nm附近的CD值，S=0 nm时CD值为0.016，S=10 nm时CD值为0.106，S=20 nm时CD值为0.192，S=30 nm时CD值为0.195，S=40 nm时CD值为0.139，S=50 nm时CD为0.043，S=60 nm时CD值为-0.061 4，S=70 nm时CD值为-0.150，S=80 nm时CD值为-0.217，S=90 nm时CD值为-0.275。

图3 不同偏移量的CD光谱

从数据中看出从S=0位置到S=30位置CD值是增加的，增加到原来的12倍。然而随着S增大到40 nm时CD值开始逐渐下降，S=50 nm时相比较S=30 nm时的CD值，下降到原来的4倍。继续变化位置，当S=60 nm时CD值变为负值，即在图3中表现为波峰位置变为波谷位置。从S=60 nm每隔10 nm变化到S=90 nm过程中CD的绝对值是逐渐增加的，增加了近4倍。从数据还可以看出S=30 nm在1 400 nm处有正向最大CD，达到0.195，S=90 nm在1 440 nm处有负向最大CD，达到-0.275。为了更深入的研究其特点，取S=30 nm和S=90 nm这两个较为特殊的情况来进行分析。

图4单独列出了S=30 nm和S=90 nm的吸收图谱和CD图谱。图4(a)所示是S=30 nm的吸收光谱，当RCP和LCP光垂直照射时，分别观察到了4个显著的共振模式，分别用Model1、Model2、Model3、Model4来表示，它们分别出现在波长为660,700,1 200,1 400 nm处，并且从图中可看出在700 nm和1 200 nm处对RCP的吸收更强，660 nm,1400 nm处对LCP吸收更强。图4(c)所示的是S=90 nm的吸收光谱，观察到了4个共振模式，同样分别用Model1、Model2、Model3、Model4来表示，它们分别出现在波长为660,720,980,1 440 nm处，而且可以看出这几个波长处对RCP光的吸收比对LCP更强。图4(b)所示为由于对LCP和RCP吸收光谱的差异所引起的CD，在Model4下即波长为1 400 nm处的最大CD值接近0.2。图4(d)所示CD，在Model4下即波长为1 440 nm处的最大CD值接近0.28。

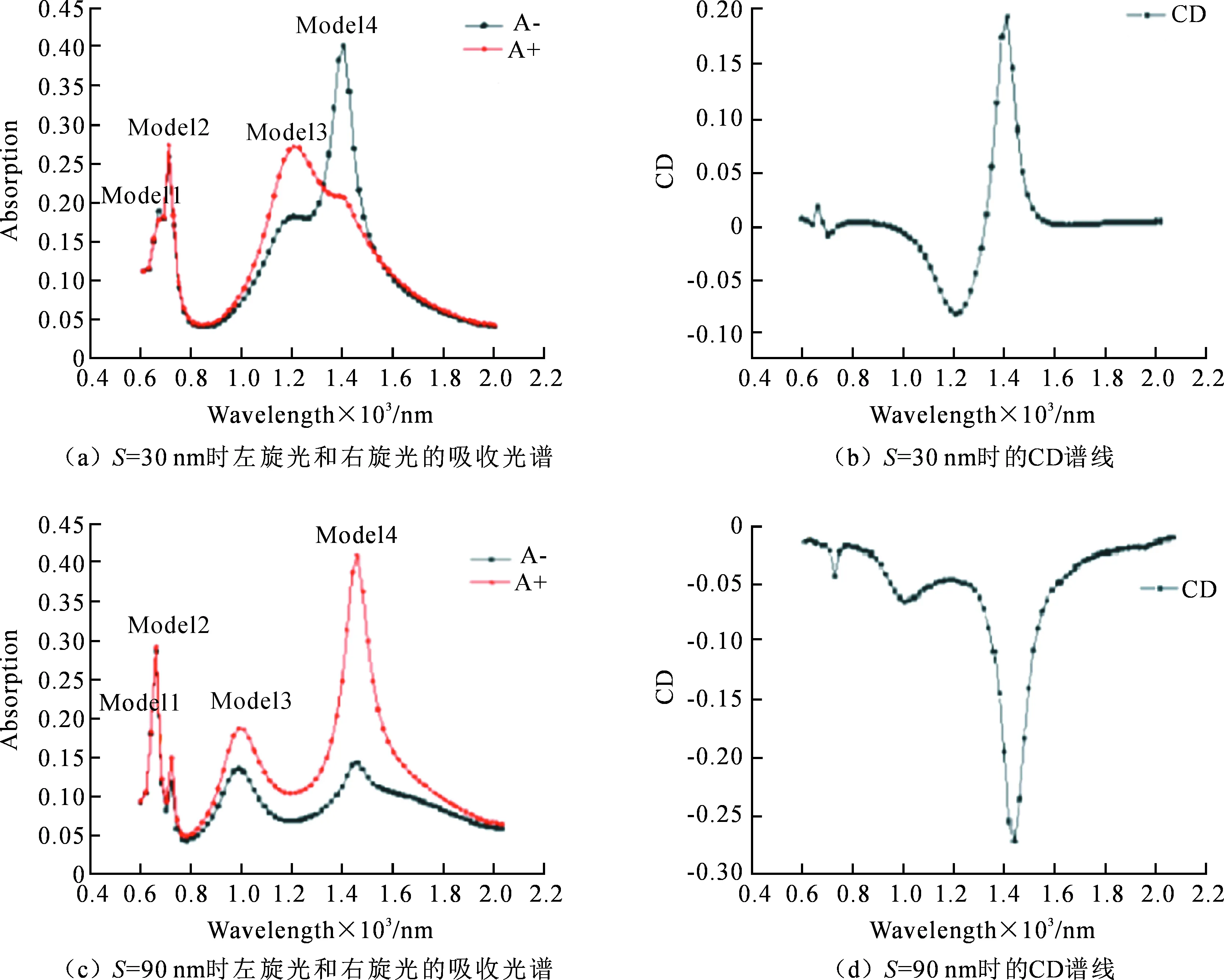
图4 S=30 nm,90 nm时的吸收光谱和CD谱线

为了研究图4中S=30 nm及S=90 nm共振模式Model1、Model2、Model3及Model4的形成原因，这里计算了S=30 nm波长为660,700,1 200,1 400 nm及S=90 nm波长为660,720,980,1 440 nm时归一化电荷分布，如图5所示，图中红色表示正电荷，蓝色表示负电荷。

从图5中可以看出结构的微小变化可引起电荷分布的明显变化，从而影响对左旋和右旋光的吸收差异，进而产生CD。

为进一步研究对称性的破坏对CD的影响，保证K型结构对称即S=0 nm，L2=200 nm，L3=200 nm，算出它对左旋光和右旋光的吸收，如图6(a)所示。然后保证其他参数不变，让L2缩短50 nm来破坏K型结构的对称性，并给出它对左旋光和右旋光的吸收，如图6(b)所示。同样保证其他参数不变时，让L2伸长50 nm破坏其对称性，也给出了它对左旋光和右旋光的吸收图谱，如图6(c)。图6(d)给出了三者的对比CD图，从图中可以看出，通过调节L2长度的变化可以大幅度的影响CD。同样也给出它们三者各自在1 400 nm附近的最大CD值，L2=150 nm时最大CD值为0.208，L2=200 nm时最大CD值为0.029，L2=250 nm时最大CD值为-0.109。从数据可以看出，通过缩短L2破坏对称性，CD值增加到原来的7倍。通过伸长L2破坏对称性，CD值增加到原来的4倍。对比三者在1 400 nm和700 nm附近的峰谷值，还可以看出，L2=250 nm相较L2=150 nm整个图谱发生了红移。

图5 S=30 nm及S=90 nm时各自的4个共振波长处的电荷分布图

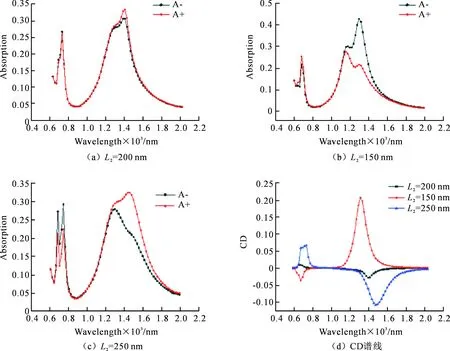
图6 L2长度变化时左旋光和右旋光的吸收光谱和CD对比图Fig.6 Absorption spectrum and CD contrast chart of L2 with different length

3 结 论

本文应用有限元方法研究了K型结构的圆二色性光谱,分析了不同偏移量S的圆二色性(CD)。K型结构的几何参数为L1=400 nm，L2=200 nm，L3=200 nm，h=40 nm，w=50 nm。保持参数不变，分析对比了S=30 nm及S=90 nm时的吸收光谱及其CD。结果表明偏移量S=30 nm在波长为1 400 nm处CD达到0.195。S=90 nm波长为1 440 nm处CD达到0.275。当S=0 nm，其他参数不变，而通过改变L2长度破坏其对称性。结果表明L2=150 nm时最大CD值为0.208，L2=250 nm时最大CD值为-0.109。研究发现，K型结构由3根线性纳米棒组成，构造简单，实验室容易制备；通过控制此结构的微小变化(S或者L的变化)，就能获得CD值的变化情况。结果显示从S=0 nm到90 nm，以步长10 nm增加时，其CD值有几个突变过程。在S=90 nm时获得CD的反向最大值，在S=30 nm时，获得CD的正向最大值。这些结果都能为设计手性光学器件等提供一定的参数指导。