垂直起降运载火箭返回轨迹不确定性优化

赵剑,黄悦琛,李海阳,*,何湘粤

1. 国防科技大学 空天科学学院,长沙 410073

2. 华阴兵器试验中心,华阴 714200

近年来,随着商业航天时代的到来,运载火箭垂直起降(Vertical Takeoff and Vertical Landing,VTVL)技术已成为国际航天领域的研究热点[1-2]。目前,VTVL技术已成为一种可行的、最具前景的可重复使用运载火箭(Reusable Launch Vehicle,RLV)的技术,极大降低了航天器发射任务的成本[3-5]。,尽管VTVL技术由SpaceX等公司进行了成功验证,但是由于返回过程中的不确定性和一些执行机构的故障,猎鹰9号在一些回收任务中仍然未能成功着陆[2-6]。引导火箭助推器返回大气层并在地球上着陆并非轻而易举的任务[7],尤其是不确定的存在削弱了返回轨迹偏差修正和精确着陆的能力,使返回过程更具挑战性[8]。因此,有必要在参考轨迹设计之初就考虑不确定性因素的影响[6],开展不确定性条件下的返回轨迹优化,提高返回轨迹的鲁棒性和可靠性,以降低飞行风险,保持制导性能并增强应急响应能力。

确保返回轨迹具有鲁棒性和可靠性的方法主要分为两类,即实施在线轨迹规划和提升离线参考轨迹的跟踪能力[9]。在线轨迹规划是根据当前状态和预测的目标落点状态之间的偏差进行轨迹重构[7]。本文主要研究提升离线参考轨迹的跟踪能力的方法,提高参考轨迹的反不确定性能力。当前关于VTVL RLV返回段标称参考轨迹的研究主要是在确定性条件下实施[10-13],以标称返回条件下由确定性优化获得的最优轨迹作为传统的参考轨迹。但是在不确定性条件下的返回轨迹优化方法少有文献研究。在不确定性因素的影响下参考轨迹的约束值将会在约束限值附近波动。因此,在存在不确定性的实际应用中,确定性解通常无法满足路径约束和终端着陆约束的要求。一个经济可行的确保实际返回轨迹鲁棒并且可靠的方法是将返回过程的不确定性因素考虑到参考轨迹的设计中来。

目前关于不确定性条件下的轨迹优化方法主要有基于可靠性的优化和鲁棒优化[14]。基于可靠性的优化强调设计的高可靠性,通过在期望的水平上保证概率约束的满足,涉及到全局优化和迭代概率评估的双过程,计算效率要求比较高[15]。诸多研究者提出了解耦优化策略[16-17],将优化环与可靠度评估环独立开来,其中由Du和Chen提出的序列优化与可靠度评估(Sequential Optimization and Reliability Assessment,SORA)方法应用最为广泛[15]。本文引入多项式混沌展开方法对SORA方法进一步改进以提高可靠度评估环节的效率。鲁棒优化侧重于通过优化系统的平均性能和最小化系统标准差,使得系统对于不确定性参数不敏感。Wang等[18]将多项式混沌展开理论与凸优化技术结合,提出了一种新的高精度、高效率的火星着陆鲁棒轨迹优化方法。罗佳奇等[19]提出考虑几何设计参数不确定性影响的叶片稳健性气动设计优化来提高叶片平均气动性能及气动稳健性。Jiang等[20-21]结合鲁棒优化策略、不确定性量化方法和伪谱方法,提出了一种在不确定性条件下的火星进入轨迹鲁棒优化方法。而在本文VTVL RLV的返回轨迹研究中,为同时兼顾并提高设计的鲁棒性和可靠性,需要将这两个性能在不确定条件下统一的模型中同时考虑,即基于可靠性的鲁棒优化[14],该方法也被用于航天器设计及其他产品设计中[22-24]。本文不选择单独的可靠性优化或者鲁棒优化方法来生成不确定性条件下的返回轨迹的主要原因有： ① 可 靠性优化通常用于获得极端情况下能够正常工作的可靠性设计,它不关注优化结果在不确定性条件下的性能损失[21],并且一子级回收问题对于着陆精度要求比较高,单纯的可靠性优化无法降低末端着陆状态对于不确定因素的敏感度；② 鲁棒优化要求所有约束都达到要求,但是一子级返回轨迹的路径约束对于不确定因素的敏感度要求不高,并且在开环的不确定性优化设计中,使得所有的路径约束都达到名义设计要求比较难以实现,而且对于性能也会有一定损失。因此,在不确定性条件下,同时考虑可靠性和鲁棒性的方法比单独的可靠性优化或鲁棒优化方法更有利于提高轨迹的综合性能[14]。

基于上述考虑,本文研究了VTVL RLV返回轨迹在不确定性条件下的优化方法。本文的创新工作主要有：① 建立了由鲁棒目标函数和鲁棒等式约束以及基于可靠度的路径约束构成的不确定性优化模型；② 基于非侵入式多项式混沌展开方法对鲁棒目标函数和鲁棒等式约束的均值和标准差进行量化处理；③ 基于非侵入式多项式混沌展开方法对的最可能点法进行改进以提高可靠度评估的效率,发展了序列优化和可靠度评估策略。该方法兼顾了鲁棒性和可靠性指标,具有较高的效率和精度。

1 返回轨迹确定性优化模型

本文所研究的轨迹优化问题仅针对VTVL RLV一子级的回收过程,因此不考虑上升段。一子级回收包括返回原场和不返回原场2种方式[25-26],本文研究不返回原场的回收方式。典型的不返回原场的一子级在完成上升段飞行后,其返回过程中通常经历调姿段、滑行段、动力减速段、大气再入段、垂直着陆段等多个飞行段[1-13]。对于不同的飞行任务,返回段划分也有所不同。考虑到调姿段、滑行段基本上均处于稠密大气层外,可以忽略气动影响[6],而调姿段也是无动力滑行,依靠反推力控制系统进行调姿[26],因此这2个飞行段均只受引力影响。本文对返回段划分模型进行简化,将返回轨迹分为调姿段、动力减速段、大气再入段和垂直着陆段4个飞行段,返回轨迹飞行剖面图如图1所示。

图1 返回轨迹飞行剖面图

在研究一子级返回轨迹的质心运动时,不考其姿态的控制调整过程。由于工程设计人员在设计之初更关注系统在平均状态下的参数,并且VTVL RLV一子级返回着陆时间较短,忽略地球的自转运动和扁率的影响,根据文献[7,13]推导了一子级返回轨迹的三自由度动力学方程,用如下的微分方程组表示:

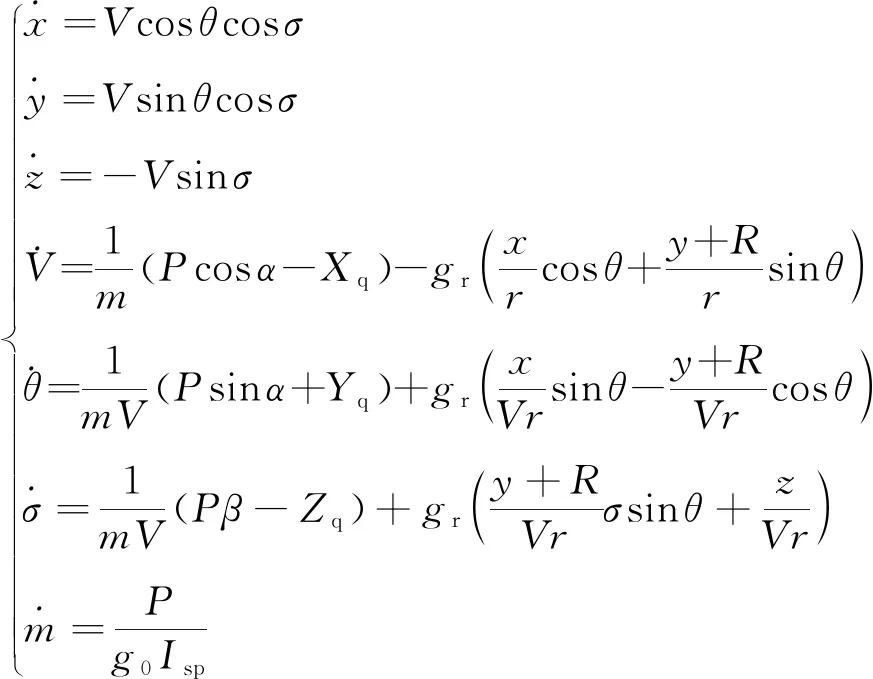
(1)

式中：x、y、z为一子级在发射坐标系中的坐标；V为速度大小；θ为速度倾角；σ为偏航角,前3个量描述了一子级在发射坐标系中的位置,后3个量描述了其速度；m为一子级质量；R为地球半径；r为地心距；P为发动机推力；Isp为发动机比冲；g0为海平面重力加速度；gr=-μ/r2(μ为地球引力常数)；α为攻角；β为侧滑角。Xq、Yq、Zq为速度坐标系下的气动力分量,定义为

(2)

式中：SM为运载火箭一子级参考面积；ρ为地球当地大气密度,ρ=ρ0e-y/h0,ρ0为海平面大气密度,h0为参考高度；Cx、Cy、Cz分别为阻力、升力和侧力系数,且Cz=-Cy,定义为

(3)

(4)

式(4)应满足初始状态约束:

x(t0)-x0=0

(5)

为使VTVL RLV运载能力最佳并有足够的燃料用于制导修正机动,一子级返回轨迹的性能指标为燃料消耗最少,即末端着陆质量最大,轨迹优化的目标函数表示为

minJ=-m(tf)

(6)

在返回的过程中路径约束主要需要考虑动压和过载的限制:

(7)

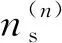
F=[F1,F2,F3,F4,F5,F6,F7,F8]T=

[n(1),n(2),n(3),n(4),q(1),q(2),q(3),q(4)]T-

(8)

着陆段终端着陆要求一子级位置和速度都要达到指定的目标和精度,同时其姿态要保证垂直。本文研究中采用位置x、位置y、位置z、速度和当地速度倾角作为终端着陆约束,则终端等式约束G可以表示为

G=[G1,G2,G3,G4,G5]T=[x(tf),y(tf),z(tf),

V(tf),θ(tf)]T-[xf,yf,zf,Vf,θf]T=0

(9)

式中：x(tf)、y(tf)、z(tf)、V(tf)、θ(tf)分别为计算得到的着陆点的位置x、位置y、位置z、速度、当地速度倾角；xf、yf、zf、Vf、θf分别为目标着陆点位置x、位置y、位置z、速度、当地弹道倾角。

从而建立了确定性条件下的优化模型,即寻找最优的控制变量u(t),使得式(6)的目标函数最优,并满足式(4)的微分方程约束、式(5)的初始状态约束、式(8)的路径约束以及式(9)的终端着陆等式约束。

2 返回轨迹不确定性优化模型

本节在所建立的确定性优化模型的基础上,引入不确定性因素,建立了由鲁棒最优目标函数、基于可靠度的路径约束和鲁棒等式约束构成的随机不确定性优化模型。本文考虑的不确定性为随机不确定性参数,假定这些不确定性参数之间相互独立且服从均匀分布。

2.1 鲁棒最优目标函数

为了提高不确定性条件下VTVL RLV返回轨迹的鲁棒性,并保证燃料消耗尽可能的小,需要在式(6)所示的目标函数中需要平衡鲁棒性和最优性。考虑到标准差可以表示不确定性条件下返回轨迹的鲁棒性,而均值可以表示其最优性,因此通过均值μ(·)和标准差σ(·)建立鲁棒优化目标函数

(10)

2.2 基于可靠度的路径约束

在不确定性条件下开展返回轨迹的优化时,路径约束可能会超过设计要求。处理该问题的一个途径是在约束限制范围内确定极端情况,然而由于一子级返回动力学的高度非线性以及不确定性的多样性,极端情况很难找到。将统计矩引入路径约束之中确实能够解决随机约束问题,但是在强非线性的返回动力学中高阶矩的约束限值难以获得,并且这种方法处理的路径约束没有明确的物理意义。本文引入概率信息,采用基于概率可靠度的方法对路径约束进行处理,它是一种在预先确定的可靠度要求下,以较小的失效概率进行优化设计的方法。

在随机空间中,引入不确定因素之后,式(4)变为随机微分方程组

(11)

式(8)的路径约束可转换为

(12)

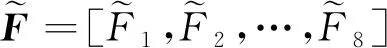
(13)

式中：可靠度向量α=[α1,α2,…,α8]T,当可靠度向量确定之后,路径约束的可行域随之确定。

2.3 鲁棒等式约束

由于优化问题在不确定条件下的概率性质,等式约束并不总是能够严格满足的,等式约束在不确定性条件下是一个随机函数,不能完全相同的等于常值。鲁棒优化中处理等式约束通常有2种方法[27]：一是完全满足均值的等式约束,在该方法中,等式约束只需满足均值设计要求即可；二是采用近似矩匹配方法,设计者可以指定关于等式约束的均值和标准差的偏好。在实际设计中,对于不同的等式约束,设计者可根据需求选择不同的处理方法。

对于式(5)中初始状态的等式约束,本文采用均值方法进行鲁棒设计,可以表示为

(14)

对于终端着陆约束,本文采用近似矩匹配方法,即基于均值和标准差的统计矩对其进行设计,即

(15)

(16)

值得注意的是,在已有的文献研究中[21],鲁棒等式约束通常如下处理:

(17)

式中：κσ为标准差对应的权重系数。

相比于式(17)将等式约束用均值和标准差的加权组合表示,本文将均值和标准差采用2个单独的约束,如式(15)和式(16)所示,虽然增加了约束的数量,但是其具有更明确的物理意义,即不确定性等式约束函数满足均值意义上的原始精度着陆要求,而其标准差有单独的敏感度约束,在均值和标准差的共同约束下构成了鲁棒等式约束。

3 基于非侵入式多项式混沌展开的返回不确定性轨迹序列优化与可靠度评估策略

本节基于非侵入式多项式混沌展开(Nonintrusive Polynomial Chaos Expansion, NPCE)方法求解鲁棒目标函数和等式约束的均值和标准差,同时基于NPCE方法提高最可能点策略[15]进行路径约束可靠性评估的效率,形成了基于NPCE方法的序列优化和可靠度评估(SORA)不确定轨迹鲁棒优化策略。

3.1 基于NPCE的鲁棒目标函数和等式约束的不确定性量化

由式(10)、式(14)～式(16)可知,在每次优化迭代中需要对目标函数和等式约束进行统计特性的求解。本节基于NPCE方法求解返回轨迹的近似解,然后通过近似解的系数获得目标函数和等式约束的均值和标准差值。

(18)

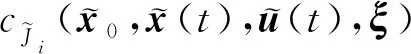
(19)

式中：iN为随机变量向量ξ每一维的展开阶数。

需要指出的是,多维随机变量的多项式基函数φi(ξ)可以通过单变量的多项式进行张量积运算得到

φi(ξ)=φj1(ξ1)φj2(ξd)…φjd(ξd)

(20)

式中：φjk(ξk)为jk∈Ni阶随机变量ξk的多项式基函数,k=1,2,…,d。

(21)

根据正交多项式的正交特性,可得

(22)

为方便推导,将式(22)中k替换为i,则多项式系数可表示为

(23)

式中：μ[·]表示期望运算。

式(23)中的期望运算可以用积分表示为

(24)

式中:f(ξ)为概率密度函数。

因此,式(23)可以进一步表示为

(25)

采用高斯加权公式近似式(25)右端的积分运算,即

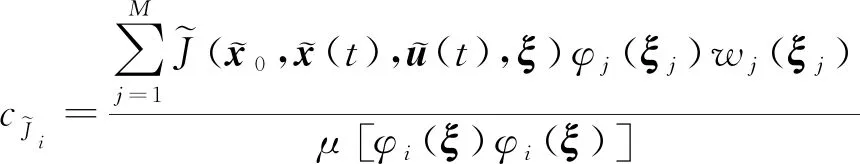
(26)

式中：ξj为随机样本积分节点;M为样本的总数;wj(ξj)为积分节点对应的权重系数;式(26)的精度可以通过增加样本数量得到提高[28]。

类比目标函数的多项式基函数系数推导过程,可得终端等式约束的系数表达式为

(27)

(28)

(29)

(30)

(31)

对于随机变量向量ξ,设其维数为d,即包含d个不确定性参数,每个分量ξi选取Mi个积分节点,通过张量网格方法得到的随机样本的总数为

M=M1…Mi…Md

(32)

式中：i∈Nd。若每一维随机变量的节点数均为Mξ,则d维随机空间总的节点数为

(33)

注意到每组节点ξj组成的样本点均对应一组R7空间下的微分方程组,因此M个积分节点对应的微分方程组可写为

(34)

式(34)满足：

(35)

式(35)为式(14)对应的初始状态约束,考虑到不确定性参数积分节点服从零均值均匀对称分布,初始状态的均值等式约束自然满足。

至此,将式(11)的随机微分方程组变为式(34)在RM×7空间下的微分方程组,将随机空间的不确定性轨迹转为高维空间下的确定性轨迹求解。在不确定性轨迹优化中,每次迭代求解鲁棒优化目标函数和鲁棒等式约束时,需要求解M×7个微分方程组,得到样本解之后根据式(26)～式(31)求解得到目标函数和终端等式约束多项式混沌展开的系数解,进一步计算得到目标函数和终端等式约束的均值和标准差表达式为

(36)

(37)

(38)

(39)

3.2 基于NPCE的最可能点法

在不确定性优化设计问题中,除了优化环节之外,还要对优化结果进行评估,分析优化设计的鲁棒性及可靠性。对于等式约束,通过均值和标准差进行约束,可保证其鲁棒性；对于路径约束,在保证样本点满足约束要求的情况下需要进行可靠度评估。基于最可能点的分析方法是可靠性评估的一种有效方法[29],能够通过优化求得所设计的可靠度对应的不等式约束限值。

考虑本文优化问题的一个路径约束:

(40)

式(40)的概率约束可以进一步表示为

(41)

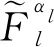
结合式(40)和式(41),可建立可靠度与其对应的不等式约束限值之间的映射关系为

(42)

(43)

式中:Φ(·)为标准正态分布函数;E(·)为累积分布函数;ul为不确定性因素ξ的函数,可将其视为ξ张成的超球面上的一个点。

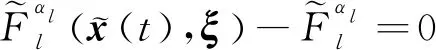
Φ(βl)=αl

(44)

由于ul为随机变量ξ的函数,其近似解析函数可以通过NPCE方法获得

(45)

3.3 基于NPCE的序列优化和可靠度评估策略

序列优化和可靠度评估(SORA)最先用于结构优化,然后逐步用于多学科设计优化[30]。本节结合前文所述的基于NPCE的鲁棒目标函数及等式约束构成的随机鲁棒优化模型、基于NPCE的改进的最可能点分析方法,展示了返回轨迹SORA方法的分析流程,如图2所示。

图2 SORA方法流程

SORA方法采用单回路策略,将问题分解为具有一系列随机鲁棒优化和可靠度评估环节。对于随机鲁棒优化环节而言,基于NPCE方法将随机空间下的优化问题模型转换为高维空间下的等价的确定性优化问题模型,从而采用轨迹优化算法如序列二次规划算法进行优化求解。对于可靠度评估环节而言,引入了基于NPCE的最可能点方法来计算要求的可靠度对应的约束限值。在每个SORA的循环中,鲁棒优化与可靠度评估相互解耦,可靠度评估只在鲁棒优化后进行,以验证不确定性条件下约束的可行性。

该方法的关键是根据前一个周期获得的可靠性信息,将失效约束的边界转移到可行方向。但是在初始迭代时,由于缺少可靠度对应的不等式约束的限值,因此考虑将名义值作为初次迭代的设计值。若不等式约束不满足所要求的可靠度对应的约束限值,则需要对约束限值进行更新,然后以更新后的约束限值代入随机鲁棒优化环节再次进行优化,而新的优化结果已不同于上一轮的优化结果,因此需要对新一轮的约束值再次进行可靠度评估,直至约束限值达到设计要求为止。一般而言,序列优化只需要有限次迭代即可收敛[31]。SORA的主要执行步骤如下:

步骤2在每一次的随机鲁棒优化与可靠度评估中,将可靠性和鲁棒性并存的随机优化问题模型转化为如下的高维空间的确定性优化问题模型进行求解：

(46)

满足：

(47)

(48)

(49)

(50)

m=1,2,…,5

(51)

式中：下标k为序列优化迭代的次数。式(46)～式(51) 将随机鲁棒优化问题模型转换为确定性优化模型进行求解,可选择合适的优化算法进行轨迹优化,图3给出了随机鲁棒优化的计算框架。

图3 随机鲁棒优化的计算框架

(52)

通过不断执行步骤2和3进行序列优化,直至MPP方法评估得到的约束限值小于名义设计值即可结束优化。

4 仿真结果及分析

表1 初始状态参数和目标着陆点状态参数

选取初始状态参数中的分离速度和模型参数中的大气密度作为不确定性参数,不确定性参数的分布如表2所示。

表2 不确定性参数

在可靠度评估环节中,各个路径约束的可靠度设计为

Prob{q(n)≤1.4×105N/m2}≥97%,n=1,2,3,4

(53)

Prob{n(n)≤9g}≥97%,n=1,2,3,4

(54)

本节设计了一个VTVL RLV返回任务来验证所提出的基于NPCE的SORA方法的有效性。数值仿真对比了基于可靠度的鲁棒轨迹优化解与确定性优化(Deterministic Optimization, DO)解。SORA和DO均选取序列二次规划算法(SQP)作为返回轨迹优化方法。在基于NPCE方法的SORA中,每个不确定参数对应的随机变量取5个积分节点,则两个不确定性参数对应的总的样本数为25个,所以在式(34)所示的微分方程组中,RM×7=R25×7,即在每次迭代计算中,需要对175维的样本轨迹进行积分运算。下面以DO轨迹解作为参考,分析SORA轨迹解的鲁棒性和可靠性,并结合基于蒙特卡罗(MC)的传统优化方法验证本方法的精度和效率。

4.1 SORA和DO方法的标称轨迹对比分析

图4展示了SORA和DO优化得到的最优控制律在标称情况下各个状态量的变化曲线。图4(a)和图4(b)分别为过载和动压随时间的变化曲线,可以看出,SORA解和DO解均在所要求的路径约束限值之内。但是DO解的过载和动压最大值接近于所设定的限值,并且SORA解的过载和动压的最大值要小于DO解的最大值,这意味着在存在不确定性的情况下,若按照DO解的最优控制律飞行,则很有可能越过安全区,飞行器在返回过程会存在很大的风险。图4(c)～图4(e)分别为末端着陆约束参数随时间的变化曲线,包括位置、速度和速度倾角变化曲线,可以看出SORA对应的标称轨迹具有与DO解近似的轨迹。换言之,从状态约束的角度考虑,SORA的最优解具有一定的DO解的最优性。但是由于SORA的最优控制律是在不确定性条件下得到的,末端着陆状态是以均值作为约束指标,所以在标称情况下的垂直着陆段末端着陆精度比DO要低,甚至有可能会出现不满足精度的情况,但是约束的偏差在飞行器调节的能力范围之内,可以通过制导控制系统修正实现精确着陆。图4(f)～图4(h)分别展示了攻角、侧滑角和发动机推力随时间的变化曲线。

总体而言,与DO方法得到的最优控制律相比,SORA所需的攻角和侧滑角的控制能力和调节范围要更大,这在动力减速段和垂直着陆段表现得尤为明显。同时,在动力减速段,SORA优化得到的发动机推力更大,从而在图4(i)的燃料消耗随时间的变化曲线中,可以发现SORA的燃料消耗要高于DO的燃料消耗质量,这是由于SORA解为均衡路径约束的可靠性和终端着陆约束的鲁棒性需要更高的控制和调节能力,以及更多的燃料消耗,同时也说明了基于可靠性的鲁棒优化不是寻找确定性最优解,而是寻找一个可靠性和鲁棒性最优的多指标最优解。

图4 标称情况下SORA和DO得到的返回轨迹

4.2 终端着陆约束鲁棒性分析

在控制律确定的情况下,本文选取的初始速度和大气密度2个不确定性因素对于燃料消耗没有影响,因此这里不需要对目标函数的鲁棒性进行分析,只需要对终端着陆参数进行鲁棒性分析。如图5(a)和图5(b)展示了终端着陆约束参数的散点偏差分布,可以发现SORA方法得到的落点所形成的包络区域在DO方法得到的落点所形成的包络区域之内。返回着陆轨迹的鲁棒性可以用标准差来衡量,为了更加直观地比较不确定性条件下的SORA和DO解的鲁棒性,通过蒙特卡罗打靶仿真,统计终端着陆点的状态集合,并使用正态函数拟合着陆点的分布情况,如图5(c)～图5(g) 所示。可以发现SORA方法得到的末端着陆点比DO方法更加接近均值纵轴,并且在均值附近的分布更密集,在两端的分布相对较小,这一点在终端速度和终端当地速度倾角上表现的尤为明显。这是由于在SORA方法中考虑了终端着陆点的标准差约束,因此相对于DO方法而言,SORA在末端着陆约束上表现出更好的鲁棒性。

图5 终端着陆约束参数的散点及概率分布

4.3 路径约束可靠性分析

本节将均匀分布的不确定性因素ΔV0和Δρ归一化到[-1,1]区间,对应的随机变量符号表示为ξv和ξρ。DO解和SORA解对应的路径约束参数峰值的分布分别如图6和图7所示。为了更加直观地表示路径约束峰值与其设计限值之间的关系,分别用过载和动压的峰值除以其设计限值进行归一化处理,若归一化的值小于1则满足路径约束,反之则不满足约束。从图6和图7可以看出,在不确定性条件下,DO的解显然超过了设计限值,在很多情况下不满足约束；而对于SORA方法,在考虑可靠性的优化中,尽管存在±30 m/s 的速度不确定性和±20%的大气密度不确定性,路径约束均满足设计要求,可靠度指标也达到了要求。

图6 DO解在不确定条件下的路径约束峰值

图7 SORA解在不确定条件下的路径约束峰值

图8为SORA和DO解的过载和动压在不确定性条件下的概率累积分布情况。从图8(a)可以看出,在过载限值为9g的情况下,DO解的可靠度指标仅为0.49。因此,尽管DO解在标称情况下路径约束满足设计限值(图4(a)所示),但是在初始速度和大气密度存在不确定性的情况下不满足可靠度要求,并且很容易陷入失效域,对飞行器带来极大的风险。同样地,对于DO解的动压而言,在动压限值为1.4×105的情况下,动压的可靠度指标仅为0.463,不满足可靠性要求。而SORA解的过载和动压约束的最值均未超过设计限值,可靠度也达到了设计要求,这证明了该方法中可靠度评估环节的有效性。

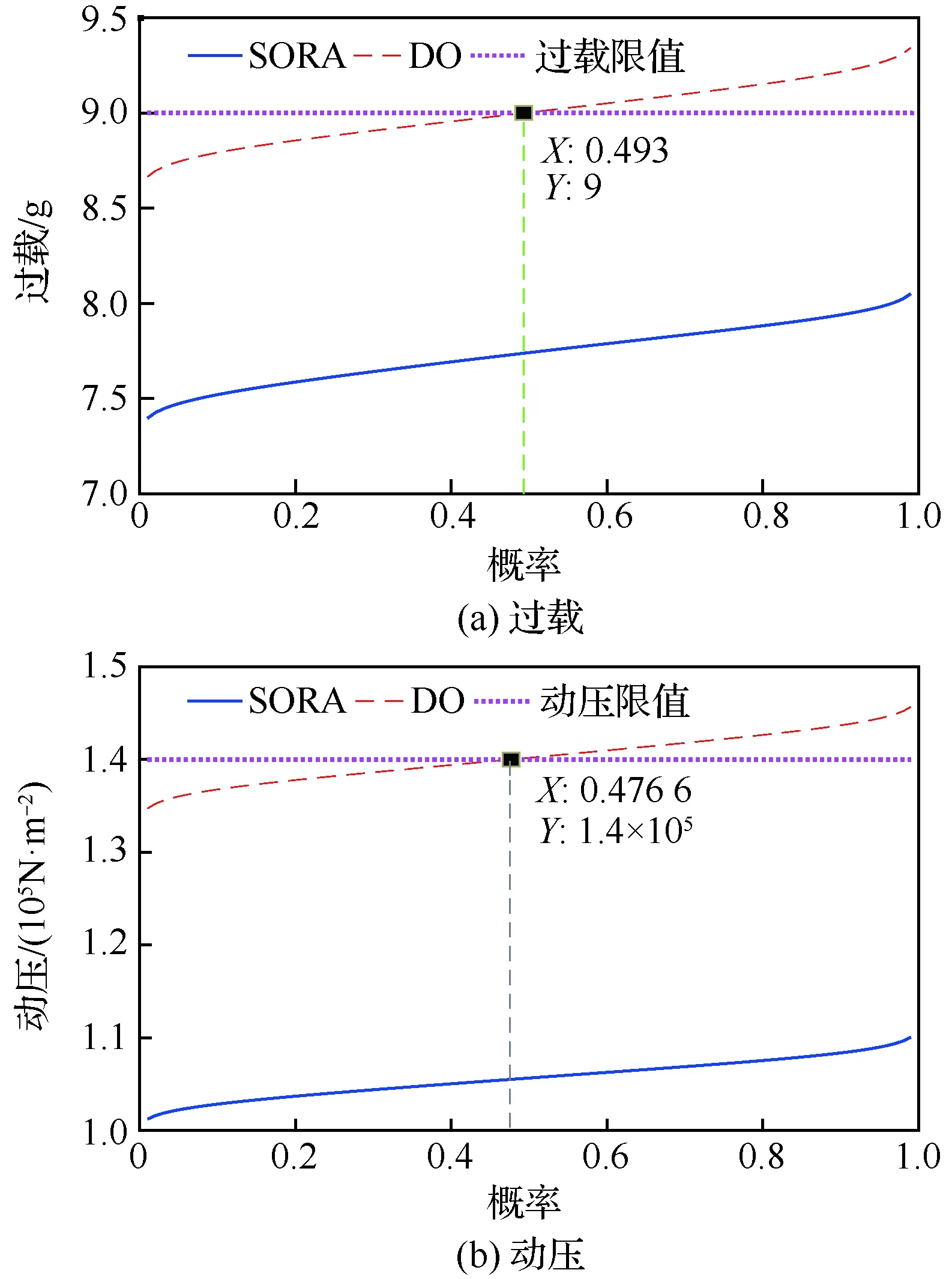
图8 SORA和DO解路径约束峰值的概率累积分布

4.4 精度和效率分析

为进一步说明基于NPCE的SORA方法的精度和效率,本节将该方法与传统的基于MC仿真的序列优化方法进行对比分析。在基于MC的可靠性评估中,采用同样的参数配置。两者的主要区别在于,在SORA的可靠度评估中,约束样本通过NPCE方法求得；而在基于MC的约束可靠度评估中,样本点通过检测MC统计值的收敛情况得到,当约束统计均值小于某一设定的偏差时则可认为其收敛。

图9给出了2种可靠度评估方法的路径约束峰值分布。可以看出,2种方法的动压和过载的都达到了97%的可靠度设计要求。2种方法的过载和动压的小偏差可以看出所提的SORA方法具有较高的精度。在两种方法的序列优化中,可靠度评估贯穿于整个优化求解过程。在基于MC的可靠度评估中,进行了3 000次样本计算后才达到收敛,可靠度评估时间接近3 025 s。而SORA的可靠度评估环节中,只需要计算25个样本点,大约25 s的计算时间。因此,基于NPCE的SORA方法在可靠度评估中具有较高的计算效率。

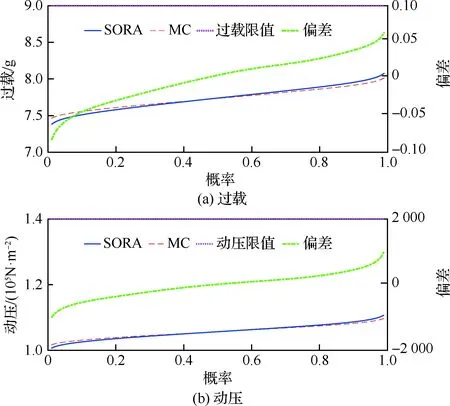
图9 基于NPCE和基于MC方法的路径约束峰值分布

5 结 论

本文针对返回轨迹存在不确定性的问题,在同时考虑返回轨迹鲁棒性和可靠性的基础上,提出了基于非侵入式多项式混沌展开的序列优化和可靠度评估策略。得出如下主要结论：

1) 建立了由鲁棒目标函数、基于可靠度的路径约束和鲁棒等式约束组成的返回轨迹不确定性优化模型,基于非侵入式多项式混沌展开方法对鲁棒目标函数和等式约束进行量化处理,将随机空间下的不确定性优化问题模型转换为高维空间下的等价的确定性优化问题模型。仿真表明,与DO方法相比,不确定优化不是寻找确定性最优解,而是寻找一个可靠性和鲁棒性最优的“次优解”。

2) 采用基于非侵入式多项式混沌展开方法的最可能点法,在要求的可靠度下评估路径约束满足的程度,进一步提高了可靠度评估的效率。

3) 所提出的基于非侵入式多项式混沌展开的序列优化和可靠度评估策略将问题分解为随机鲁棒优化和可靠度评估环节,提高了轨迹解的等式约束的鲁棒性和路径约束的可靠性,同时也具有较高的精度和计算效率。

总之,本文所提出的不确定性优化方法增强了参考轨迹的跟踪能力和反不确定性能力,提高了返回轨迹的鲁棒性和可靠性,对于中国未来垂直起降可重复使用运载火箭的发展具有一定的理论研究价值和工程参考意义。