重复使用运载器制导与控制技术综述

宋征宇,蔡巧言,韩鹏鑫,王聪,潘豪,张广春,李栩进

1. 中国运载火箭技术研究院,北京 100076

2. 中国运载火箭技术研究院 空天业务部,北京 100076

3. 北京航天自动控制研究所,北京 100854

具有重复使用的天地往返能力,一直是航天工业界和学术界努力的目标。美国航天飞机具有这样的能力,但高昂的维护成本,最终导致其退役。航天飞机项目之后,各国积极探索基于火箭动力/吸气式组合动力的单级入轨、多级入轨重复使用天地往返运输系统方案,近年多家商业公司也在探索火箭一子级垂直起降方案,重复使用运载器技术将迎来快速发展契机。

美国自20世纪50—60年代起通过航天飞机首次实现了航天运载器的部分可重复使用,并陆续开展了下一代运载器技术[1]、美国空军军用空天飞机[2]、低成本响应空间运输[3]、美国空军完全可重复使用进出空间计划[4]等一系列可重复使用运载器研究项目,提出了“狮鹫”运载系统[1]、“天狼星”新型运载器[5]、混合动力水平起降运载器概念[6]、“隼”式混合动力发射系统[6]、Quicksat空间作战飞行器[2]、兰利滑翔返回助推器[6]、ARES混合动力发射系统[3]、X系列验证飞行器[4]、Hyper-X、XS-1[7]。进入21世纪,以SpaceX[8]、蓝色起源(Blue Origin)[9]、马斯腾[9]等诸多商业公司为代表,积极开展了垂直着陆回收的可重复使用火箭研制,尤其助推级可复用的Falcon9火箭已投入商业市场。

欧洲早在20世纪70年代起就围绕可重复使用运载器技术开展了大量研究工作。通过未来欧洲航天运输革新计划[10]、未来备用运载器研究计划[11]、下一代运载器[12]、先进航天运输优势研究[13]等诸多的研究计划,提出了多种单级入轨/两级入轨运输系统方案,陆续研究了亚轨道重复使用运载器系统(HOPPER、Phoenix等)[10]、部分可重复使用的空间运输系统[13]、液体推进飞回式助推级[14]、Bargouzin运载系统[15]、阶段性试验飞行器[16]、Adeline验证机[17]、SKYLON[18]等飞行器,并开展了相关飞行试验验证。

20世纪80年代日本提出20吨级的HOPE小型无人航天飞机,并确定先研制不载人的有翼飞行器,最终实现运载器的完全重复使用。在此之后,其重点转移到新一代大型运载火箭的研制计划上。通过低成本上升飞行试验、OREX轨道再入试验、HYFLEX高超音速飞行试验等一系列飞行试验,促进可重复使用技术的发展和完善,为尽快投入工程应用奠定基础[19]。

俄罗斯自“暴风雪”号部分重复使用航天飞机系统终止之后,20世纪90年代初,先后实施了基于Molniya小型航天飞机的多用途航空航天发射系统(俄语缩写MAKS)、“贝加尔号”等重复使用运载器计划[18]。同时,自20世纪60年代以来,以中央空气流体动力研究院为代表的多家研究机构,持续开展以吸气式发动机为动力的可重复使用运载器基础理论研究[20]。

印度2005年启动重复使用运载器技术验证项目论证,宣布了返回飞行试验、超燃冲压推进试验、着陆飞行试验等重复使用技术验证项目,2012年开始项目样机研制[21],2016年RLV-TD完成首次飞行试验[22-23]。

本文重点对重复使用运载器的制导与控制技术进行综述。第1节介绍国际上重复使用运载器的发展途径和分类,并对垂直起飞垂直着陆、垂直起飞水平着陆、水平起飞水平着陆等特点,以及对制导与控制的需求进行了介绍和讨论。第2节建立了较为统一的重复使用运载器数学模型,以便更清晰地梳理不同飞行模式在制导与控制方面的差异。第3节分别就不同工作模式下制导与控制技术的研究成果展开讨论。第4节梳理了未来的发展趋势,并对发展重点进行了总结。

1 发展途径与需求分析

按照不同的分类标准,重复使用运载器可分为多种不同类别,如图1所示。本文主要根据起降方式的特点展开分析。

1.1 垂直起飞垂直着陆(VTVL)

美国Blue Origin和SpaceX公司火箭回收方案的实现和工程应用,标志着垂直起降运载器已成为重复使用技术发展的一种新途径。

Blue Origin于2015年11月率先在New Shepard火箭上实现了垂直起降,飞行高度达到100 km,验证了着陆支腿控制、环箭体减速舵面控制效果、着陆支腿展开、着陆段制导控制等算法,该火箭还可用于验证NASA登月精确着陆系统等试验项目。在此基础上,Blue Origin正在研制New Glenn重型火箭,近地轨道运载能力达到45吨,可实现一级回收[24]。

SpaceX首先在蚱蜢飞行器上开展了8次飞行试验,飞行高度达到744 m,验证了悬停、侧向转移、风干扰条件下的垂直着陆等项目；进一步研制了三发动机并联的F9R-Dev飞行器,共开展5次飞行试验。此后利用Falcon 9在完成载荷发射任务后,开展了6次助推级海面降落试验,验证了高空高速返回全程多飞行段的制导控制技术,并于2015年12月实现了陆上垂直回收。2018年2月SpaceX研制了3个助推级模块并联的Falcon Heavy重型火箭,同时对2枚助推器开展返回原场的垂直回收,并对芯一级在分离后进行海上垂直回收[25]。在SpaceX正在开展的火星登陆项目中,其Star hopper飞行器完成了低空垂直起降的飞行试验,以单台偏心发动机的状态实现了着陆,星舰SN10也完成了首次高空飞行测试与定点着陆。

法国国家空间研究中心(CNES)、德国宇航中心(DLR)、日本航天开发机构(JAXA)结合各自在垂直着陆技术上的经验,正在联合研制CALLISTO飞行器[26-27]。3个组织都将利用该飞行器验证各自的制导控制算法,最大飞行高度可达到40 km,速度达2马赫。在此基础上,欧洲航天局(ESA)将研制Themis火箭作为欧洲可重复使用技术的里程碑验证项目,分为单台发动机和3台发动机2个阶段,最大速度可达到6～8马赫,模拟火箭高速进入稠密大气层内的动力减速、气动减速全部过程[28]。经过验证的重复使用关键技术将应用于Ariane Next系列火箭[29]。

中国运载火箭技术研究院也开展了关于垂直起降的关键技术研究和演示验证工作[30]。各团队的研究路线如图2所示。首先开发算法,并设计或租用算法验证飞行器对制导控制技术开展攻关；然后结合火箭动力系统,研制垂直起降原理样机,验证实际动力系统条件下制导控制算法的效果,以及其他各系统之间的匹配性；随后研制可发射有效载荷的可重复使用运载器,并回收助推或芯一级火箭；最后将垂直起飞垂直着陆(VTVL)技术用于入轨运载器的重复使用。

图2 垂直起飞垂直着陆运载器研制路线

上升段飞行需要考虑火箭回收级的分离约束条件,即在保证能够完成任务的同时,为着陆段提供较好的交班条件。同时需要合理规划回收级的剩余燃料,既能够一定程度上适应返回过程中的偏差和干扰,又要减小对上升段主任务运载能力造成的损失。上升段姿态运动模型参数具有慢时变的特点,受到弹性和推进剂晃动运动影响,具有不确定性,且在大风区受气动影响较大,姿态控制方法必须能够适应上述特点。

着陆下降段,再入稠密大气的过程需要考虑动压、热流、过载等再入约束,通过主发动机减速控制,在节省燃料的同时,调整再入弹道指向着陆场。控制系统需要保证箭体准确到达预先指定的着陆区域,并以精确的姿态垂直软着陆。制导系统还需在满足约束的前提下,尽可能减小发动机开机的台数和次数。若发动机调节能力有限,则可能出现回收过程中推力始终大于箭体自重的情况,极大压缩了动力软着陆段的物理可行域；这就对气动减速段的控制精度提出了更高要求,也使得在同时满足终端速度、位置、姿态等约束条件时更为困难。鉴于此,更优的制导方法需要利用剩余燃料提升适应能力,而非以燃料最省作为目标。对于姿态控制,需增加返回时用于辅助姿态稳定控制的气动舵和反作用控制系统(Reaction Control System, RCS)装置。其中,RCS主要用于再入大气前火箭主发动机不工作时的姿态调整与稳定；再入大气后展开气动舵,利用空气动力进行姿态稳定和气动减速。下降段环境变化复杂、动压剧烈变化、多类执行机构交替复合工作等特点,造成了更为显著的不确定性和内外部扰动。特别是着陆支腿展开过程中,箭体质心和压心的变化,以及支腿展开不同步对姿态的冲击,都会导致较大的建模不确定性。

1.2 垂直起飞水平着陆(VTHL)

2000年以来,美国空军围绕快速响应进入空间的目标,持续发展火箭动力垂直起飞、带翼水平返回的一子级方案[31]。从战神(ARES)[3]、可重复使用助推器系统[32]到目前的XS-1[33-35]方案,VTHL的一子级关键技术持续取得突破。除美国外,俄罗斯和印度也开展了类似的研究。

VTHL上升段具有传统运载火箭的特点,主发动机工作时间短(一般不超过10 min),在此期间动压和过载变化大,飞行器受的干扰和对控制力的需求变化也很大,同时需解决面对称构型带来的新问题。例如,在相同风干扰条件下面对称飞行器有更大的控制力需求,更易产生三通道间的控制耦合。在采用主发动机推力矢量进行姿态控制的同时,可采取气动舵面减载措施,以降低舵面的铰链力矩。

返回段升力式再入具有常规飞机的特点,不仅有动压、过载、热流和平衡滑翔等约束条件,而且以到达机场跑道为终端目标,实现在预定着陆场水平着陆。返回段进一步细分为：① 初期再入段,重点解决大攻角再入时减速和航程控制问题；② 末端区域能量管理段,重点应对初期再入末端的散布问题；③ 进场着陆段,解决在预定着陆场无动力水平着陆的问题。

全程姿态控制存在以下突出的特征和难点：

1) 在垂直上升阶段不能采用航空飞机上通常采用的气流角(攻角、侧滑角)反馈,而必须采用运载火箭常用的姿态角反馈控制模式。

2) 大翼展面对称体在高超声速下存在显著的横、航向控制耦合特性,导致存在荷兰滚模态不稳定、副翼操纵不利于偏航、大攻角飞行状态下操稳性能下降等问题,尤其是滚转通道常出现副翼滚控反效现象。反效对姿态稳定影响最为严重,更为致命的是由于气动规律的不确定性和天地不一致性,实际飞行中副翼反效出现的时机、可行的判断切换逻辑难以精确确定,控制律设计必须要避开可能的副翼反效区间。

3) 飞行剖面涵盖亚音速至高超音速、地面至轨道空间,大气数据系统尚无法做到航空领域的成熟度和工程应用精度；没有较可靠的传感器直接测量攻角和侧滑角,其估计值存在着一定的误差,这就要求控制系统必须具备足够的鲁棒性来克服误差的影响,并采用必要的等效测量信息进行稳定控制。

4) 结构静弹性变形引起舵效差异、动态气动伺服弹性带来控制稳定裕度严重损失甚至不稳定；整个工作过程中飞行剖面速域和空域、舵面使用范围变化跨度大,气动弹性变形、气动伺服弹性的规律和变化幅度差异显著。

5) 升重比低导致高速自主着陆控制精度对干扰敏感,缺乏高保真的着陆滑跑动力学、纠偏/转弯运动学模型。

尽管可借鉴航空领域水平着陆模式,但是重复使用运载器为了兼顾低速和高速段的综合飞行性能,需满足不同速度下的升阻比需求。在进场着陆的低速段升重比相对飞机而言偏低,进场速度(350～ 380 km/h)远高于航空飞机正常着陆接地速度(多低于280 km/h)。这使得着陆精确姿态控制对速度、姿态约束极为敏感,低空突风、地面顺逆/侧风干扰影响显著。同时,触地后缓冲及高速滑跑过程中,飞行器与地面间相互作用的运动学和动力学响应特性难以精确建模,只能通过简化模型进行控制律仿真评估,更多程度上需要靠基于真实产品的滑跑试验进行验模和控制律修正。目前除空中投放之外,还缺乏其他有效验证方法和手段。

1.3 水平起飞水平着陆(HTHL)

该运载器的飞行剖面涉及稠密大气、临近空间、近地轨道,涵盖亚跨声速、超声速、高超声速整个速域,依靠单一发动机难以满足任务要求,通常采用多模态组合的吸气式发动机[36]。飞行器的动力学特征表现为明显的气动力/气动热/发动机/弹性/控制耦合现象,造成制导控制设计过程中约束复杂且约束的形式变化多样。

吸气式组合动力系统上升段的飞行性能与飞行轨迹密切相关,发动机推力与燃料流量均具有非定常快时变特点,且气动力、发动机推力、机体姿态与轨迹之间存在强耦合关系,吸气式发动机对攻角和侧滑角有严格的强约束要求。其返回着陆方式则与VTHL的返回段类似。

HTHL上升和再入过程中的飞行走廊狭窄,非线性强,使得在不同工作点上的线性化模型差异很大,导致线性控制方法的效果及鲁棒性能不佳。但若应用经典的非线性控制方法,需要对模型非线性项进行多次求导或递推,导致项数膨胀和运算负担过重的问题。因此需要研究具有强鲁棒、自适应能力的控制方法。同时,由于机体发动机一体化设计、自身弹性结构和高速飞行的特点,动力学耦合特性非常突出,单一的控制参数和结构往往难以满足期望的控制指标和品质。

2 制导与控制问题描述

制导与控制技术的持续发展,其目的是为了能够更好地适应被控对象的运动特性、满足运动过程中存在的约束条件和任务目标,从而提升被控对象的偏差适应性和任务适应性。可重复使用运载器的质心运动和绕心运动模型、各飞行阶段的约束条件和控制目标共同构成了可重复使用运载器制导与控制技术面临的问题,与制导控制技术的发展密切相关。

本节描述了VTVL、VTHL、HTHL三类可重复使用运载器的质心运动和绕心运动方程,根据各飞行段的特点,总结了复杂约束条件；并通过设计合理的目标函数,提升制导控制算法对偏差和不确定性的适应能力。

2.1 运动模型

在惯性坐标系下描述质心运动方程,包含位置、速度和质量随时间的变化规律；在箭体坐标系下描述绕心运动方程,包含绕心刚体运动方程、弹性和晃动运动模型。定义m、r、V分别表示质量、位置矢量、速度矢量,ω为绕箭体轴转动的角速度矢量,G和F分别为运载器受到的引力和其他作用力,J和M分别为箭体转动惯量和力矩,下标T、R、A、s、e、D分别表示发动机控制力(矩)、RCS控制力(矩)、气动力(矩)、晃动力(矩)、弹性力(矩)、干扰力(矩),则可重复使用运载器运动方程可表示为

(1)

式中：g0为海平面重力加速度；Se为喷口截面积；Pe为设计状态大气压强；Pa为外界大气压强；FA和MA与运载器飞行状态相关,可表示为

(2)

MT为由发动机摆动产生的三轴控制力矩,与发动机推力和摆角相关。

弹性力矩Me可表示为

(3)

按有限元法建立弹性振动建模:[37]

(4)

推进剂晃动力矩可分为法向、横向和轴向三部分,以推进剂法向晃动力矩(Ms3)为例:

(5)

描述法向晃动的运动方程为

(6)

需要指出的是,式(1)描述的运动方程为多维、非线性、变系数运动方程组,需将其在平衡点附近进行小偏差扰动线性化[37],简化为相互独立的运动通道用于稳定性分析和设计。

2.2 端点和过程约束

2.2.1 上升段约束条件

1)初始状态约束

以起飞时刻t0作为运载器的初始时刻,垂直起降运载器依靠发动机产生大于地球引力的推力实现起飞,起飞时刻的位置即为发射点位置,速度为地球自转在发射点产生的速度,起飞质量即为初始质量。水平起飞的运载器则依靠升力抵消地球引力的影响,需考虑离地速度、滑跑距离S、滑跑轮载Nwheel等约束。综上,初始状态约束如表1所示。

表1 上升段初始状态约束

2) 过程约束

运载器在大气层内飞行时,需满足过载(N)、动压(q)、弯矩(qα)约束,以保证结构安全；受执行机构控制能力限制,需满足舵摆角(δ)约束和舵面负载(MH)约束；为保证姿态稳定,需满足姿态角和姿态角速度的约束。垂直起飞运载器主要考虑俯仰角(φ)、偏航角(ψ),以及相应角速度(ωφ,ωψ)的约束；在起飞后短时间(t1)内需保持竖直上升,即推力方向uT垂直于水平面。对于水平起飞运载器,由于气动力是克服引力影响的主要作用力,需重点考虑攻角(α)、侧滑角(β),以及相应角速度(ωα,ωβ)的约束条件,同时考虑发动机工作模态保持和切换过程的特殊约束(α、β、h)。上升段过程约束如表2所示。

表2 上升段过程约束

3) 终端约束

垂直起飞和水平起飞运载器的终端条件一致。考虑回收级分离时刻速度、位置与着陆时射程相关,需要保证在一定偏差范围内(或者射程在偏差范围内)；同时引入分离时刻质量约束,为着陆段预留足够的燃料/能量。对于分离时刻与着陆时刻状态,回收级存在连接两个状态点的标准弹道,即分离时刻状态约束也可采用轨道根数表示。具体终端约束如表3所示。

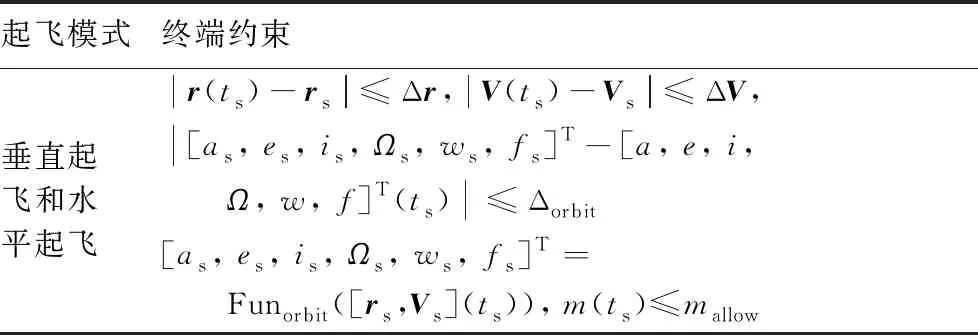
表3 上升段终端约束

2.2.2 返回下降及着陆段约束条件

1) 初始状态约束

着陆过程初始状态为ts时刻状态:

[r,V,m](ts)=[rs,Vs,ms]

(7)

2) 过程约束

垂直着陆过程包括惯性调姿段、动力减速段、气动减速段和动力软着陆段4个飞行阶段,需将全部约束条件合理分配在各飞行阶段。运载器通过控制发动机秒流量调节推力幅值,因此对于无动力飞行段,秒流量始终为零；对于有动力段,秒流量按照发动机调节能力在[dmmin, dmmax]范围内调节。在惯性调姿段,需考虑初始状态约束、角速度约束；在动力减速段,考虑发动机秒流量约束、角速度约束的同时,还要重点考虑热流、动压和过载约束对火箭的影响；在气动减速段,火箭的质量不变,气动力作为火箭的主要控制力,需满足热流、动压和过载约束。在动力软着陆段,由于速度和高度相对较小,可以忽略热流、动压和过载约束对火箭的影响,仅考虑角速度约束、角度约束和终端状态约束条件,以及剩余可用燃料约束。

姿态角速度作为运载器着陆过程的控制变量,其幅值会影响到姿态控制系统的稳定性,特别是在进入稠密大气层后,可允许的姿态角速度小于稀薄大气飞行段。在最后精确动力软着陆段,发动机推力很大,推力方向任何细微的调整都将对绕质心运动产生很大的力矩作用,影响姿态控制系统的稳定性,此时姿态角速度要限制在非常小的范围内,同时也要将表示火箭姿态角的推力方向限制在一定范围内。与上升段类似,着陆过程中也需要满足舵摆角、舵面负载约束。

水平着陆模式包括初期再入、能量管理、无动力进场着陆3大阶段,初期再入段需考虑动压、热流、过载约束；能量管理段除角速度、姿态约束外,要重点考虑飞行能量与航程、机动要求、过载、动压约束；无动力进场着陆段考虑飞行姿态、动压约束的同时,还需重点考虑减速板偏角、下降速度、下滑高度对触地条件的影响。

具体约束条件如表4所示。

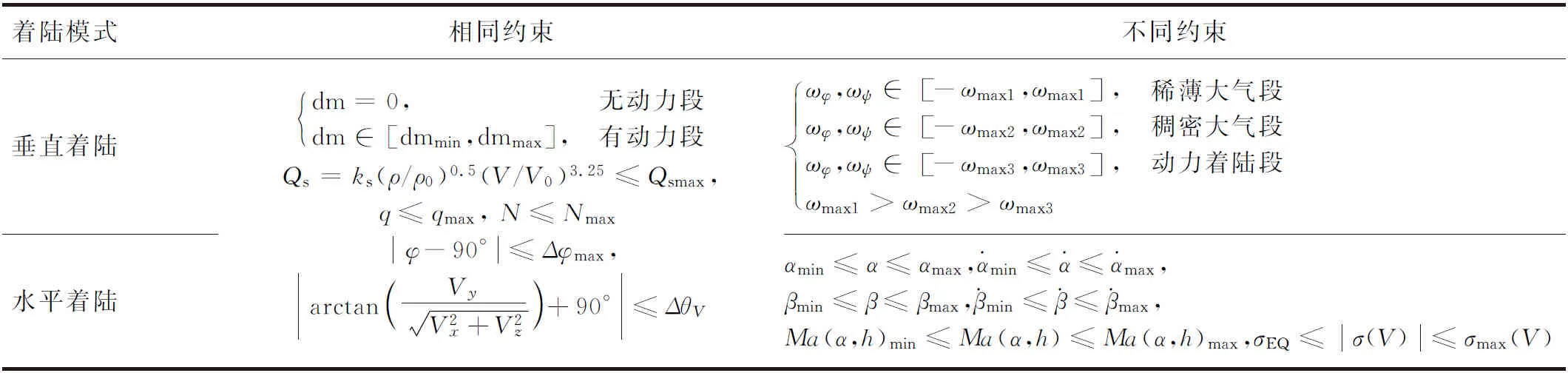
表4 返回及着陆段过程约束

3) 终端约束

对于垂直着陆,为实现定点软着陆,运载器在着陆时刻(tf)的位置需要在着陆区范围内(采用经度λ和纬度B表示),终端纵向速度必须向下,且幅值小于火箭着陆支腿可承受的最大触地速度Vy fmax,水平面内两个方向的速度小于箭体可能导致倾倒的最大横侧向速度Vxz fmax。终端姿态角度和速度倾角最大偏差较过程约束更小,用Δφf和ΔθVf表示。着陆过程中质量在分离时刻剩余质量和结构质量(mend)之间。

对于水平降落运载器,需要考虑着陆时刻的下沉率(dh)、触地速度(Vdown)、滑跑距离、滑跑轮载、刹车量约束(FB),从而保证运载器能够安全平稳着陆。在姿态方面需要考虑姿态角约束(α,β)、触地姿态角(φ,ψ,γ)和角速度(ωφ,ωψ,ωγ)约束,通过调整姿态尽可能降低垂直于水平面方向上的速度和加速度,确保着陆的下沉速度、水平速度及姿态在合理范围内。

着陆段终端约束见表5。

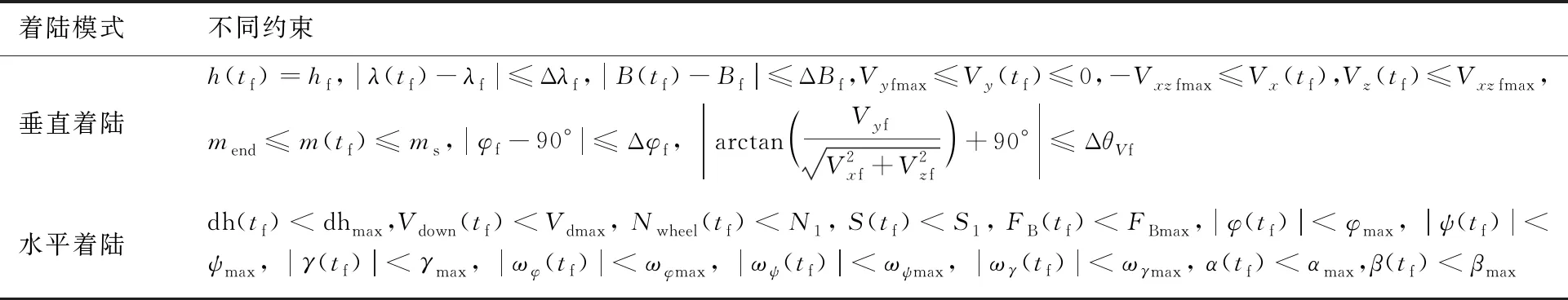
表5 着陆段终端约束

2.3 目标函数

2.3.1 上升段目标函数

由于分离状态即为回收级初始状态,要求可重复使用运载器尽可能处于理想状态,从而降低着陆段或无动力段的修正压力。因此上升段制导的目标函数可表示为最大化分离时刻回收级剩余质量和最小化终端状态偏差的加权和形式。

(8)

通过权重系数λr、λV、λorbit调节比重。若仅约束终端速度和位置,则λorbit=0；若仅约束终端轨道根数偏差,则λr=λV=0。

在上升段,姿态控制系统除保证运载器稳定飞行外,还包含铰链力矩峰值最小和伺服峰值功率消耗最小两个目标:

(9)

2.3.2 返回下降及着陆段目标函数

对于垂直回收着陆段,一种朴素的想法是尽可能靠近标称轨迹,则目标函数可表示为

(10)

若不考虑标称轨迹,制导目标是在满足全部约束条件和尽可能节省燃料的同时,提升着陆精度,目标函数可表示为

(11)

从制导算法鲁棒性的角度考虑,尽可能提升回收级飞行过程中的抗干扰能力是提高回收成功率的有效手段,通过评估着陆段物理可行域边界(rb,Vb),导引回收级尽可能远离可行域边界,则目标函数可表示为

(12)

对于水平着陆的飞行器,带动力返回飞行过程中的目标函数与垂直着陆回收模式相同；无动力返回水平着陆模式下,还需保证返回过程中任意时刻能量e状态下的剩余航程Stogo(e)与达到着陆场校正圆柱所需航程SHAC之间满足安全余量约束,同时尽可能缩小Stogo(e)与SHAC之间的偏差,从而实现安全到达预定着陆区：

J5=Stogo(e)-SHAC≤J0

(13)

式中:J0为考虑飞行器升阻特性散布和环境干扰因素影响所确定的航程能力安全余量。

不同性能指标函数对制导方法的要求也不同。从经典的PID控制,到基于数值优化的模型预测控制,均可用于以跟踪为目标的制导方法；受不同算法对问题的简化程度和控制指令形式的限制,生成制导指令的控制效果存在差异。但若性能指标中不考虑标称轨迹,则需要通过在线规划或预测校正等方式生成制导指令。

从姿态控制的角度,需要考虑铰链力矩峰值最小、伺服峰值功率消耗最小、无动力返回飞行状态距离姿控能力边界尽量远、消耗的RCS发动机燃料最小等需求,

(14)

3 可重复使用运载器制导和控制方法

结合3类可重复使用运载器的特点、约束条件和控制目标,制导与控制方法的目标是能够实时计算满足全部条件的最优指令,因此逐步发展出了近似条件更少、考虑约束更多的先进方法。本节梳理了制导与控制方法的研究现状、发展脉络和方法特点。

3.1 VTVL制导和控制方法

3.1.1 制导技术

1) 上升段制导

各国运载火箭早期的上升段制导方法均是开环制导[38-40],即通过离线弹道规划获得将有效载荷送入目标轨道的位置、速度和推力方向指令(程序角)随时间的变化规律。火箭起飞后,可选择时间、速度或高度作为自变量,插值获得相应飞行状态下的程序角,从而实现对火箭质心运动的控制。这种方法一般以表3中标准入轨点处的速度、位置作为终端目标,且时间插值程序角消耗燃料最多,速度插值最省燃料。开环制导使用的控制指令能够在大气层内满足载荷约束,结合发射日预测风场规划弹道能够提升开环制导的适应性[41]。在火箭进入真空环境后,不再需要考虑表2中qα约束条件,利用闭环制导算法自主生成最优程序角,以目标轨道参数作为终端目标,能够大幅提升制导精度[42]。典型的解析最优制导方法包括应用于火箭的迭代制导(Iterative Guidance Mode, IGM)[42-47]、应用于航天飞机的动力显式制导(Powered Explicit Guidance, PEG)[48-50]、及基于变分法的最优制导(Optimal Guidance, OPGUID)[51-52]等。

IGM以最优控制原理为基础,通过解析公式迭代计算到达目标轨道所需的速度增量、位置增量,并依此规划出最佳飞行程序角[44-45],该方法启动时刻越靠前,跨飞行段的处理越复杂,但故障适应能力越强。中国长征系列运载火箭在IGM的研究中也取得了显著的成绩。2011年11月CZ-2F/Y8发射任务中首次使用了跨推力段的迭代制导方法。CZ-7采用了预测修正IGM,可省略末速修正系统实现大推力下的高精度直接入轨。2020年9月CZ-2F/T3发射任务中,首次使用了带终端姿态约束的迭代制导方法,在省略调姿系统的条件下,同时实现了轨道根数和终端姿态的高精度控制[46]。在2020年12月CZ-8首飞发射任务中使用了跨滑行段的迭代制导方法,满足低倾角和大椭圆转移轨道发射需求。

PEG是一种不依赖标准轨迹的半解析预测校正算法,根据变分法推导最省时间入轨问题的线性正切制导律,使用待增速度求解协态变量,并通过估计关机时刻的速度偏差来修正待增速度[50]。OPGUID从土星火箭到航天飞机时期,一直作为IGM和PEG的备份算法,能够满足包括Euler-Lagrange方程在内的全部最优性必要条件,但算法的成熟度仍有待提高。

IGM和PEG在对发动机故障状态的适应性、鲁棒性、目标性能、扩展性和灵活性等方面的表现基本一致,而OPGUID的优势则表现在假设条件较少[52]。此外,NASA马歇尔中心还研究了在进入真空前接入迭代制导的可行性,通过对输出指令的约束,也能够满足载荷约束条件,并且相比于开环制导终端状态散布更小[40]。

为尽可能降低助推级回收的燃料消耗,助推级分离时刻的控制精度十分关键,而这给摄动制导方法[53]创造了应用条件。该方法基于摄动理论,将火箭上升段运动过程分为慢变和快变两部分,可使火箭在理想弹道附近飞行,导引火箭获得理想的分离条件[54]。崔鑫水提出了长征运载火箭的摄动制导方法[55],通过离线计算导引系数,生成飞行过程中的导引系数插值表,并实时计算飞行状态与理想导引量的偏差,从而生成导引指令；配合弹道规划离线生成的程序角指令,能够获得较好的分离控制精度[56-58]。

为提升飞行适应性,在满足结构载荷约束的前提下,在线生成大气层内飞行程序角指令是重点研究方向之一。随着箭载计算机能力的提升,发展出了基于数值优化理论的飞行轨迹在线规划方法,也称计算制导方法。当规划周期满足制导需求时,可代替已有的解析方法；在实时性不足时,可与制导算法结合,在线更新标准轨迹。计算制导主要包含间接法[59-61]和直接法[62-65]两类。Sun采用间接法中的有限微分方法求解控制指令,通过同伦方法处理大气密度,达到了在线生成上升段制导指令的目的,在主发动机推力损失的故障状态下具有一定的适应能力[59]。

2) 着陆段制导

对于着陆段,针对动力软着陆段的研究最为广泛。按照计算特点主要可分为解析制导、计算制导、基于学习的制导方法3类。解析制导通过简化着陆问题从而得到与实时飞行状态相关的制导律,主要包括以PID、线性二次型调节器(Linear Quadratic Regulator, LQR)等经典控制为代表的跟踪制导[66-68],已应用于阿波罗、嫦娥三号等任务的多项式制导[69-71],基于最优控制的ZEM/ZEV(Zero-Effort-Miss/Zero-Effort-Velocity)制导[72-75]。解析制导律是离线推导和设计的,但这类方法几乎都无法考虑表4中的着陆段过程约束,离线设计和装订的控制方程仅能适应标准弹道附近的小偏差工况；对于再入环境复杂的可重复使用火箭,很难推导解析制导律。

计算制导利用数值优化算法在线求解包含着陆段的运动方程(式(1))、约束条件(表4、表5)和目标函数(式(10)～式(13))的优化问题,获得飞行轨迹和最优控制指令[76-78]。其中基于凸优化的直接法已被应用于工程[79-85],而求解非凸问题的方法受限于理论上的收敛性尚未工程应用[86-89]。算法不受标准轨迹的限制,具有更强的适应性；但是对于非凸约束和多飞行段优化问题,仍无法满足在线应用要求。

美国JPL在2012年开展了自主上升与下降动力飞行试验项目的研究,使用Xombie飞行器,验证了基于凸优化算法的在线轨迹规划方法,并开发了一种燃料最优大范围转移的制导算法,完成了750 m大范围移动飞行验证[90]。CNES研制了基于涡喷发动机和挤压式火箭发动机的两款FROG飞行器,设计了基于PID和LQR的着陆段标准轨迹跟踪制导控制算法,完成了20 m高的悬吊飞行试验[67]。DLR研制了EAGLE飞行器,用于验证在线轨迹规划、PD跟踪制导控制等,并开展了1.2 m高的悬吊飞行试验[91-92]。JAXA研制了RV-X飞行器,并计划开展百米高的垂直起降飞行试验[93-94]。在国内,北京航天自动控制研究所、翎客航天等也研发了验证性飞行器对相关算法进行验证[95]。

基于学习的着陆段方法主要包括深度学习[96]和强化学习[97-98]两类。在离线训练时考虑各种约束条件和性能指标的作用,将训练结果提炼成易于计算的控制方程和控制逻辑,获取满足着陆过程约束的控制模块(神经网络、模糊控制器等),便于箭载计算机实时计算控制指令。但是真实训练样本不易生成,而基于模型的训练结果又和实际飞行过程存在一定偏差,对于离线未覆盖的情况很难保证控制指令的最优性或有效性。

气动减速段的制导方法研究不多,但这段飞行过程中受到的不确定性扰动最大,环境也最复杂[99]。Lu提出了基于预测校正的气动减速段再入制导算法以提升着陆精度[100]。

动力减速段修正上升段偏差,使火箭沿理想着陆轨迹飞行；通过主发动机点火,满足再入过程中过载、热流、动压等约束。可以将动力减速结束后的飞行轨迹视为目标轨道,采用IGM[101]或闭路制导[102-103]计算制导指令。该飞行段需要在关机后保证气动减速段再入约束的峰值不超限的同时,减少持续动力减速消耗的燃料。

3.1.2 控制技术

目前,多数运载火箭姿态控制系统是利用经典的单回路频域法或根轨迹方法设计[104-105],该方法可以清晰的揭示系统性能和动态特性的变化趋势,且现行的飞行品质要求也大多数是根据经典控制理论提出的,设计依据充分。当考虑垂直起降过程建模不确定性、参数变化以及内外部扰动剧烈等更为复杂的工况时,包括反步控制、滑模控制、鲁棒控制、自适应控制等[106]新的控制方法引起了关注。

1) 上升段控制

火箭高速穿过大气层,受气动影响大；尤其飞经大风区时,考虑箭体气动承载能力限制,需要主动减载控制。目前主要有基于加速度表信息[45]和基于自抗扰算法的主动减载控制[107],两者分别被应用于CZ-7和CZ-8运载火箭[45]。Simplicio等[108]提出了一种通过干扰观测器预测风扰动的减载控制策略。通过扩张状态观测器或干扰观测器在线辨识风干扰,并进行实时补偿控制是实现减载的有效途径,已进入实际工程应用。

为克服箭体弹性、晃动等附加运动导致的飞行品质下降,重型运载火箭太空发射系统(SLS)的飞行控制设计采用经典控制器和自适应增强控制器相结合的方式。Orr等[109]以模型参考自适应控制方案为基础,利用前向增益调制律,增强在极端非标称情况下的鲁棒性,NASA还利用F/A-18战斗机对该方法开展了飞行测试[110-111]。SLS中的自适应增强算法扩展了稳定裕度,为固定增益控制器提供额外的鲁棒性和适应性[112]。

在主动弹性抑制方面,除传统的陷波滤波器设计方法外,Mao等[113]将模糊逻辑和自适应控制相结合设计了一种自适应模糊滑模控制律,采用假设模态法和“加勒金”方法建立气动弹性模型,并利用反步法设计双闭环子系统控制器；其中每个子系统采用滑模控制器保证控制指令的跟踪,同时利用模糊逻辑系统结合自适应技术对非线性部分进行逼近,提高了姿态跟踪控制性能。

2) 滑行调姿段控制

通过RCS进行调姿和稳定控制,并实现推进剂沉底以满足发动机点火要求。姿控喷管的控制主要有非线性设计方法、相平面法、最优控制方法以及自适应控制方法。王勇等[114]提出了基于最优控制的断续姿控系统二次型开关控制方法,并推导得到了系统姿控精度模型,描述了最优控制设计相对于非线性设计的性能优势。Xing和Parvez[115]提出了滑模鲁棒控制,利用相对姿态运动学和动力学方程构造控制律,通过将原问题转化为调节问题实现了高精度跟踪控制。

晃动是液体火箭需要重点关注的因素。大幅度调姿会导致推进剂大幅度晃动,严重影响控制性能。Shtessel和Hall等[116-117]研究了弯曲模态和晃动模态对运载火箭动力学的影响,利用滑模观测器重构柔性体和晃动模态,并设计了能够补偿弯曲和晃动影响的控制器。Pei等[118]提出了利用自适应增广控制器实时抑制火箭的晃动不稳定性,并开展了四旋翼无人机加悬挂质量结构模拟运载火箭圆柱形贮箱内液体推进剂旋转晃动的验证。

3) 动力减速段控制

通过摇摆发动机实现飞行姿态稳定控制。对于垂直着陆,当着陆支腿展开时,由于展开过程箭体质心、惯量变化大,导致箭体特性存在较大差异,也给姿态控制设计带来了难度。

将模型不确定性和外部扰动视为整体扰动,采用干扰观测器估计扰动,并在控制器中补偿其影响。Hall和Shtessel[119]针对级联不确定系统和可重复使用运载火箭系统设计了一种连续滑模控制方法,以提供滑动模态所需的最小增益,在外界干扰、不同任务轨迹和建模不确定时保持了良好的鲁棒性。Tian等[106]基于多时间尺度平滑二阶滑模控制器和干扰观测器设计的姿态控制策略,在模型参数不确定性和未知外部干扰下,实现了姿态的快速跟踪而不产生控制抖振。Wang等[120]利用滑模面采用指数函数特点,使滑动变量快速收敛；并用连续项代替符号函数,消除传统滑模控制的抖振问题；利用非线性观测器用来处理不确定性,以解决反步控制的固有“项爆炸”问题。文献[121]提出了一种基于自适应反步控制和快速终端滑模控制的有限时间姿态控制器,利用自适应律来估计不确定项的界,保证了姿态角的稳定跟踪。文献[122]将鲁棒自适应控制综合到反步控制过程中,应用于可重复使用运载火箭再入段姿态控制。Mao等[123]利用模糊逻辑系统结合自适应技术对系统不确定项在线建模,设计了基于自适应模糊控制方法的姿态跟踪和补偿控制器。

各种控制方法通过对主动抑制干扰,并融合辨识方法提高控制的稳定性与自适应能力。

4) 气动减速段

本飞行段,火箭飞行姿态跟随实时生成的制导指令,完成气动减速及一定程度的横侧向机动,利用气动舵和姿控喷管进行复合控制。

针对异类执行机构控制效率和动态特性的差异,及气动舵面效率随飞行速度和高度变化对复合控制的影响。文献[124]将RCS和气动舵合并简化为一套执行装置,按照动压和攻角的变化,进行控制力矩在线分配。文献[125]使用离散脉宽脉频调制方法设计RCS控制器,通过动压的变化改变气动舵面的偏转,以完成混合控制逻辑设计。

5) 垂直着陆段

由于箭体速度低,气动舵效率减小,主要依靠发动机摇摆进行高精度姿态控制。由于对着陆速度、位置和姿态均有严格要求,在浅层风和结构干扰等影响下,使制导与姿态控制铰链耦合严重,多约束下的安全着陆控制成为一大难点。各种以强适应性为目标的辨识与自抗扰控制方法是主要的研究方向。Huang等[126]设计了自抗扰姿态控制,获得了较好的控制精度,并对稳定性进行了证明；SLS的自适应增广控制方法也可以借鉴使用[109-112]。

3.2 VTHL制导控制方法

3.2.1 制导技术

1) 上升段制导

针对典型的升力式面对称构型,气动力对轨迹特性的影响比轴对称构型火箭高一个量级,风干扰下飞行轨迹具有一定的减载效果。X-33采用的在大气层内开环制导方式[127-128],会导致返回初始状态偏差散布过大,难以满足运载器在预定机场安全着陆的需求。因此,典型的制导方法是跟踪离线设计的标称轨迹,采用根据速度和高度偏差对弹道倾角进行补偿的制导方案,或采用反馈线性化等方法跟踪标称轨迹[129-131]。

孙春贞等[132]提出基于有限微分的上升段制导方法,达到了在线生成制导指令的目的,在故障状态下具有一定的适应能力。文献[129]将上升段标称轨迹按飞行时间进行阶段划分,然后采用微分方法来求解两点边界约束问题得到轨迹控制量。文献[130]按时间划分飞行轨迹并构建哈密顿函数,将飞行约束转换为协状态方程,采用最优控制理论求解轨迹控制量。

2) 初期再入制导

再入制导的任务是引导飞行器再入过程安全,精确进入末端窗口。标称轨迹法和预测校正法是常用的两种方法。

标称轨迹法在航天飞机的再入制导中得到成功应用[127,133-134],将总体约束直接转化为阻力加速度剖面内的上边界和下边界,从而形成再入飞行走廊；在走廊内设计标称轨迹,并按航程要求设计纵向二维轨迹剖面,不考虑横向航程。航天飞机以固定迎角剖面飞行,通过控制滚转跟踪标称轨迹,本质上是PID制导律[135]。

在航天飞机之后,标称轨迹法由离线规划向在线规划发展,从二维扩展到三维。典型方法包括准平衡滑翔制导[135-138]和衍化的加速度再入制导(Evolved Acceleration Guidance Logic for Entry, EAGLE)[139-142]。准平衡滑翔制导将过载、热流、动压等过程约束转换为攻角/倾侧角制导指令边界,并根据能量或航程偏差在线生成可行域内的纵向/横向制导指令。EAGLE将纵向加速度制导扩展到三维加速度制导,可以提高再入航程的计算精度；利用滚转角和迎角来控制轨迹,制导参数采用反馈线性化设计,具有较高的鲁棒性和自适应性。上述方法采用平衡滑翔、线性大气模型等假设条件进行在线求解制导指令。

Youssef和Lu等以X-33为背景提出了适应性更强的预测校正制导方法[143-146]。该方法依据再入初始和目标条件,通过数值积分在线预测整段弹道,然后通过搜索算法调整控制输入,最终输出制导指令。该方法对环境及初始位置不确定性具有较好的鲁棒性,但受限于求解实时性和收敛性问题,仅在个别工程项目的再入飞行阶段进行了工程应用。

为进一步提升自主飞行的能力,在线搜索满足全部约束的三维轨迹,能够提升环境不确定性的适应能力。其中基于粒子群(Particle Swarm Optimization, PSO)的轨迹规划方法实现简单,具备较好的全局搜索能力[147-148],且配合多核嵌入式处理器能够提升求解效率；荣思远等[149]对不可行粒子再利用,并结合变异策略对种群多样性进行准确控制,从算法上提升了求解效率。

3) 能量管理制导

该技术继承了航天飞机的成果[134,150],忽略飞行器纵向航程和横侧向机动距离之间的耦合作用,跟踪离线设计的二维轨迹,满足飞行走廊约束(能量与待飞距离即剩余航程的关系)。目前已发展出在线生成飞行剖面的制导方法,避免大能量偏差下的轨迹跟踪误差问题。根据高度、动压与待飞距离的关系分别定义高度基准剖面和动压基准剖面,前者采用一次直线和三次曲线组成的固定形状,后者采用两段折线组成的剖面。横侧向制导指令则根据飞行过程的状态实时采用固定大小的滚转角指令调整指令方向,以适应横侧向机动较小、初始能量较大的飞行剖面。随着计算能力的提升,X-33、X-34跟踪二维轨迹制导方法的计算效率得到了提高[127-133,151]。美国Draper实验室提出了一种基于蛇形机动横侧向轨迹的三维轨迹跟踪制导方法[142],考虑了纵向和横侧向的耦合作用,可以同时生成纵向和横侧向指令,适用于初始能量较小、横侧向机动较大的飞行器。

4) 进场着陆段制导

在工程上多采取基于标称轨迹剖面的制导技术[152-153]和基于在线轨迹生成的自适应制导技术[154-159]。航天飞机离线设计了4条轨迹作为不同质量和能量状态下的着陆标称轨迹[152]。为克服轨迹设计与制导控制强烈耦合的缺点,Barton和Tragesser[159]提出了高度剖面设计方法,使得轨迹可以摆脱制导控制而单独设计与仿真,大幅增强了任务轨迹的鲁棒性。

Schierman等[156]研究了无动力着陆在线轨迹生成技术和轨迹修正算法,并在X-40A的模拟飞机平台上进行了应用[160]。其特点是在离线轨迹数据库基础上对离线轨迹进行编码,通过实时飞行状态和临界参数在线辨识出合理的轨迹。虽然解决了在线计算速度和解收敛问题,但其工程应用性仍有待进一步解决。

3.2.2 控制技术

在控制律设计上,仍以“PID控制律设计+增益调度”为主[107]。航天飞机早期的横侧向控制中采用“航向控滚转”的横侧向控制方案[161],多次飞行之后针对过分依赖航向RCS这一缺点,提出了一种在3马赫以上采用反副翼控制,3马赫以下采用常规控制的的横侧向控制方案[162]。X-33飞行器的控制方案之一是非线性动态逆与神经网络智能控制融合的方法[163-165],同时以X-33为对象还提出了滑模控制[166-169]、适应反馈线性化控制[170-172]、轨迹线性化控制[173-174]。其中滑模控制容易实现有线时间内收敛,但是控制抖振无法消除且可能激起系统未建模动态；轨迹线性化控制相当于不需要插值的增益调度控制,但是缺乏带宽设计的统一准则、只能获得沿标称状态的指数稳定；上述控制方法均有待实际飞行应用验证。

近年来,关于VTHL水平返回控制方法的研究十分活跃,基本可以分为以下几类,其中多种方法的结合尤其受到关注：

1) 自整定PID方法：将经典PID方法与优化算法(例如遗传算法、神经网络)或模糊数学结合,使PID控制器参数具备自整定能力以提高自适应性[175]。该方法作为一种基本控制设计方法,结合运载器特性在各个飞行段均可应用。

2) 滑模控制：滑模控制变结构系统在空间飞行器控制方面已取得进展[116,176-177],在再入非线性特性较大,或大角度机动时,使系统按期望的动态特性超平面滑动至稳定原点,该方法在抗干扰和姿态跟踪方面具有一定优势。

3) 自适应控制：利用Lyapunov理论设计控制算法,通过信息采集、参数辨识、性能分析确定控制策略,控制参数随时间可变[178]。该方法通常与其它方法组合使用,通过对干扰的在线辨识与补偿控制,提高飞行的可靠性与适应性。

4) 鲁棒控制：使用固定的控制结构,考虑实际系统与数学模型之间的偏差,使得在偏差状态下满足稳定性与其它性能指标[179-181]。鲁棒控制对稳定能力具有较强要求,设计较苛刻,可应用于气动影响小的无动力飞行段,易于实现。

5) 动态逆法：实现非线性控制系统反馈线性化设计,对于大攻角再入、跨声速等模型非线性较强的飞行阶段有较好的控制效果[182]。

6) 自抗扰控制：不需要准确识别干扰参数,可减小内、外部干扰以提高鲁棒性[183]。

此外,以神经网络学习和模糊控制技术为突破口,出现了鲁棒自抗扰控制[184]、预设性能控制[185]、有限时间控制[186]为代表的改进型控制方法,进一步拓展了解决思路,但尚待应用验证。

3.3 HTHL制导与控制方法

HTHL模式下,吸气式飞行器主要采用行业标准程序POST和OTIS离线优化飞行轨迹,目前已应用于多个组合动力飞行器的方案论证[187]。制导方法需重点解决飞行走廊过窄的问题,并在故障下能实现自主应急返回。目前受姿态约束影响,主要采用跟踪制导方法[188]。

基于在线轨迹规划的计算制导方法同样适用于组合动力上升段,但求解稳定性较差,需设置合理的约束及初值,使用复杂。较多文献中尝试将一些结构/飞行器方案相关的因素引入至优化问题的控制量中,尽可能模拟组合动力飞行器实际飞行情况[189-193],从而增加了优化过程的约束变量。常用轨迹优化方法有：高斯伪谱法[189]、增广拉格朗日遗传算法[191]、模型预测静态规划[194]、结合机器学习的粒子群[193]等方法。

由于组合动力发动机的性能与飞行环境密切相关,为保证其稳定工作在一个最优或稳定状态,在吸气式阶段多采用跟踪动压剖面的方法设计制导律。该方法简单,计算迅速,稳定性好,虽然不是最优解,但在一定程度上考虑了发动机和飞行性能的影响。组合动力飞行器在达到一定高度和速度后,可采用等动压爬升方法[195]来确保发动机性能最优。该方法根据动压与飞行速度和大气密度之间的关系,借鉴指数形式大气密度公式,设计出高度-速度剖面,满足按照某一动压常数爬升的需求；当飞行速度一定时,等动压爬升高度更高。借鉴该思想,贾晓娟和闫晓东[196]针对涡轮基组合动力飞行器,利用热流爬升的思路弥补了等动压爬升方法忽略的热流约束,并利用反馈线性化的方法设计了攻角制导指令。一些学者还提出了基于权系数自适应理论、神经网络理论等的在线攻角剖面规划制导方法[194,196],但组合动力飞行器的飞行包络对飞行攻角、高度、速度3个量均有较苛刻的约束,在线计算往往难以快速求得甚至更多情况下难以找到可行解。

在控制方法上,PID控制器仍是工程应用领域的首先方案,X-43和X-51两款组合动力飞行器就采用了增益预置PID控制器[36]。其他研究集中在鲁棒控制、滑模变结构控制、自适应控制、预测控制等。

针对组合动力飞行器面对称构型下强耦合特性,通过多通道舵面交联控制以抑制通道之间的耦合影响,特殊工况下利用飞行器在特殊阶段的耦合特性降低控制压力[197-198]。兰利研究中心针对耦合引起的LCDP(Lateral Control Departure Parameter)不稳定问题,就是采用副翼反操纵的策略进行滚转控制[199]。

采用六自由度耦合模型以适应动力学特性复杂、飞行约束苛刻且约束多变/快变的特性,也是组合动力重复使用运载器飞行控制的技术途径之一,例如采用小增益控制[200]、反步控制[201]、动态面控制[202]、全状态反馈等完成高阶非线性模型的控制器设计[187]。

3.4 制导和控制方法小结

综上,本节根据算法表达形式,比对分析了VT、VL、HT、HL 4个飞行段的不同方法。

表6总结了VT飞行段制导方法。基于解析方法的制导律具有形式简单、计算快的优点,最早使用离线规划的开环制导指令,但该方法对于产品偏差、环境不确定性等干扰的适应性很弱,在分离时存在较大的状态偏差。为提升适应性,发展出了能够根据当前飞行状态的反馈生成制导指令的摄动制导,使运载器的飞行轨迹尽可能接近标称轨迹,但其很难兼顾全部轨道参数的精度。真空飞行段,以IGM和PEG为代表的制导方法利用最优控制原理推导近似燃料最优的解析制导指令,不依赖标称轨迹,在实现高精度入轨的同时,对飞行过程中的干扰,甚至是某些故障具有较好的适应性。计算制导由于能够考虑更多复杂约束条件在线规划飞行轨迹和制导指令,对故障的适应能力强于解析闭环制导；在无法到达原目标轨道时,能够在线规划最优救援轨道,解决了IGM仅能飞向固定目标轨道、PEG需要装订大量离线策略实现故障救援的问题,但是计算快速性和收敛性仍有待改善。

表6 VT制导方法

表7总结了VL飞行段制导方法。通过对着陆问题简化,基于最优控制理论推导出的多项式制导、ZEM/ZEV反馈制导、闭环制导相较于跟踪制导不再以靠近标准弹道为目标,而是根据飞行状态计算最优制导指令,从而提升了着陆精度。数值方法的特点在于能够考虑更多的过程约束,通过滚动时域的方式生成制导指令；模型准确度越高,则算法的控制效果越好,因此通常需要与在线辨识算法配合使用。但数值方法在复杂约束条件下的收敛性不易证明,且通常对初值猜想要求较高,并且间接法还需要对协态变量进行猜想,实现复杂。基于凸优化的方法是一种在特定约束下保证收敛性的快速计算方法,对初始猜想不敏感；但复杂约束条件下的序列凸优化方法收敛性仍较难证明。此外,在垂直着陆中,现有的方法均认为发动机推力连续可调,并且着陆前推重比可以接近于1,这也是目前成功实现着陆应用的火箭均普遍采用多台发动机并联的原因。对于大推重比下的定点软着陆,可为现役运载火箭的复用升级提供条件,已经引起了学者的关注[203]。基于学习的方法通过离线训练生成控制网络,便于在线迅速计算制导指令,但存在学习目标设置困难、对于超出训练集的状态适应性不强等问题。

表7 VL制导方法

表8总结了HT飞行段制导方法。HT运载器需要在大气层内实现冲压发动机的稳定工作,为满足其苛刻的工作条件,开环制导和只适合真空段的IGM、PEG等解析方法不再适用。以跟踪制导为基础的剖面法,形式简单、计算迅速、稳定性好,在离线设计中考虑了发动机和飞行性能的影响；但是在飞行状态偏差较大的情况下,受姿态约束限制很难实现在约束管道内对标准剖面的跟踪,且其常用的单通道设计导致了在最优性方面存在损失。基于数值的方法虽能够重新规划以获得新的飞行剖面,但计算过程复杂,受到飞行走廊窄、气动控制强耦合的影响,求解稳定性较差,只能在合理初值条件下收敛。

表8 HT模式下制导方法对比

表9总结了HL飞行段制导方法。剖面法在初期再入、能量管理、进场着陆段均可应用,但是不利于大能量偏差下的制导。数值预测校正制导实现对飞行过程中的控制参数序列的修正,适应性和鲁棒性均优于解析方法；但通常需进行纵向、横向控制的解耦设计,以降低求解问题和控制序列的复杂度,其中基于瞬时反转逻辑的横向制导律通常无法考虑姿控回路跟踪延迟的影响,对于存在禁飞区或航路点等过程约束的问题较难求解。基于准平衡滑翔条件的制导方法能够与预测校正制导结合,提升对过程约束和飞行走廊的适应能力。基于EAGLE的方法可求解三维加速度制导律,提高再入航程的计算精度。在线轨迹规划能够处理禁飞区、航路点等复杂过程约束,对于突发事件或飞行异常状态具有较好的适应性,但同样存在实时性和收敛性的不足。

表9 HL返回段制导方法

表10总结了各种控制方法。

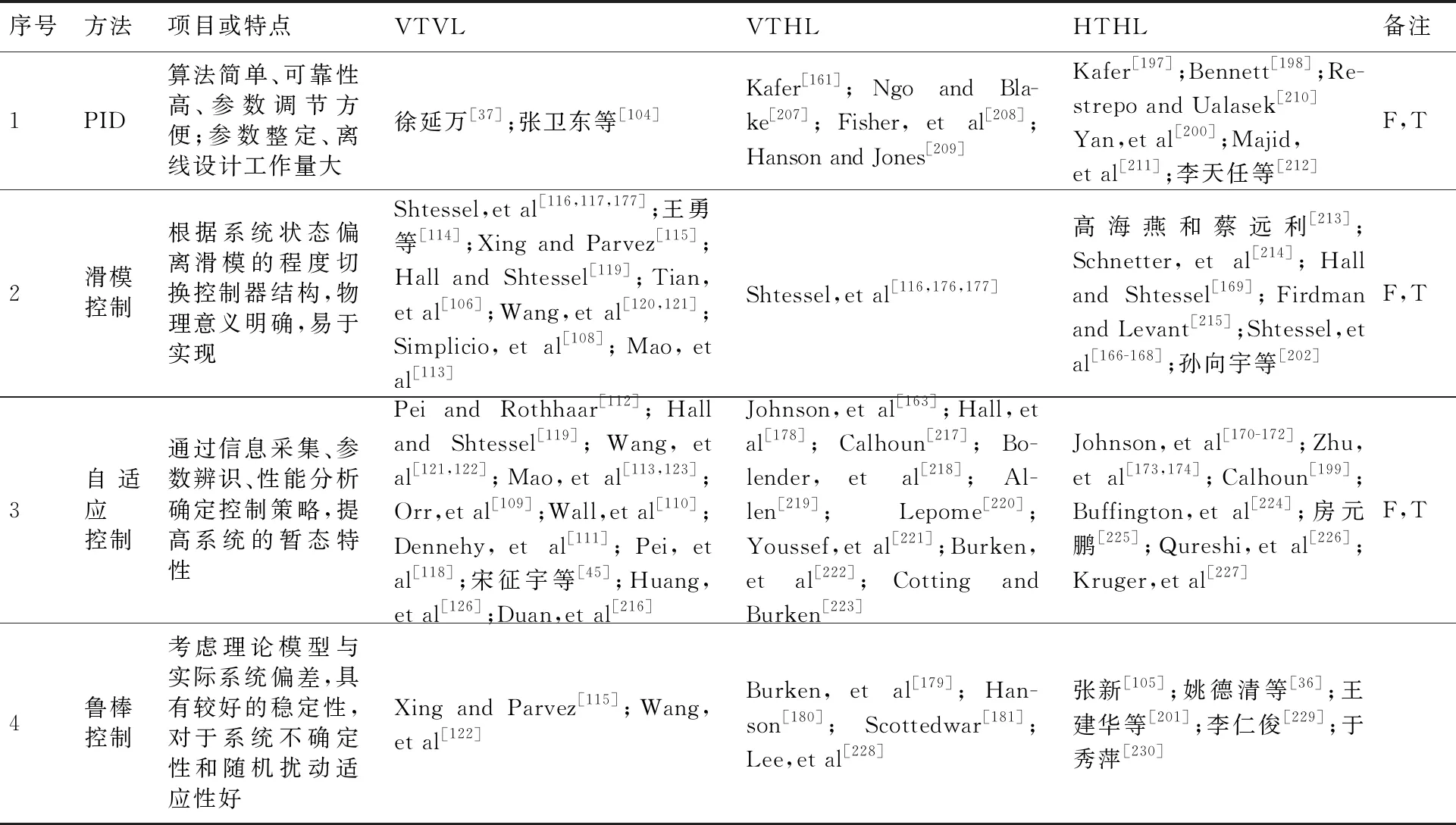
表10 VTVL、VTHL和HTHL的常用控制方法

1) 姿态控制主要研究方向是结合PID控制的辨识与自适应控制方法,其中基于滑模控制和自适应控制的多种非线性控制方法的综合成为了研究重点。

2) 对于存在严重的非线性、不确定性、干扰以及通道耦合的模型,滑模控制足够简单高效,对被控对象的模型误差、参数摄动以及外部干扰具有很好的鲁棒性。但在状态轨迹到达滑模面后,难以严格沿着滑模面向着平衡点滑动,而是在滑模面两侧来回穿越,会引起“抖振”现象；为此多采用与观测器相结合的控制策略。

3) 自适应控制能够很好地解决模型中的不确定性,并且对先验知识所需较少,因此正在被越来越多地采用。

工程应用需针对飞行器动态特性,选择匹配的控制方法并尽量精简设计。通过多种方法结合并发挥各自优势,是一种稳妥可行的技术途径。

此外,基于人工智能(AI)的控制方法也在不断发展,但在重复使用运载器的应用中还有待验证,限于篇幅,本文对这方面的研究未过多地评述。

4 发展趋势与展望

采用垂直起降(VTVL)的方式实现可重复使用,已被SpaceX公司的Falcon9火箭所验证；同一枚火箭从回收到再次发射的周期最快已缩短至38天。但多台发动机并联的配置,并非在役运载火箭普遍采用的方案。如果发动机配置少或节流能力弱,整个动力着陆段推重比均大于1,不具备匀速下降能力,并使得可行域大幅收窄。这就要求制导控制算法应确保交接班条件位于较窄的可行域内,远离可行域的边界,并能够快速消除因不确定性和干扰导致的影响,避免在推力处于饱和状态下因应对干扰而偏离可行域[231]。如果采用先进的制导方法解决在大推重比下着陆的难题,就可以在不改变发动机配置和火箭构型的情况下实现对现役火箭的回收,其意义将更为显著。

在垂直着陆中另一个研究领域是制导控制与着陆机构的一体化设计,将原有的终端约束,转变为避免火箭倾倒和箭体结构及支腿在冲击下破损等更为一般性的约束,从而放宽对速度和姿态的约束,增大垂直着陆的概率；并降低对结构和机构承载的要求以实现轻质化设计。

在VTHL以及HTHL方面,还未出现可提供商业服务的产品。这类运载器为充分利用气动升力作用多采用大翼展的升力体布局,由此带来一系列制导与控制难题。无动力返回大机动过程中还需重点关注剩余推进剂在贮箱内大幅晃动的动力学响应及其对制导控制的影响,并有可能对第3节中的相关模型进一步完善。

组合动力重复使用运载器还面临多种工作模式切换的挑战,尤其是动力系统模式切换和执行机构切换,需要满足不同发动机特性、工作条件等的约束,相当于进一步增大了过程和边界约束；同时这些约束将直接影响速度、位置等状态量,增加优化命题解析求解或数值计算的难度。

综上所述,本节梳理了可重复使用运载器制导控制技术的发展脉络,并结合工程经验展望了发展趋势,如图3所示。

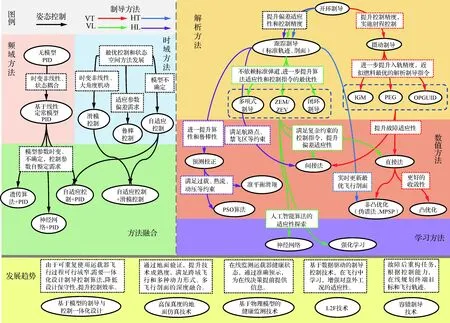
图3 可重复使用运载器发展脉络

重点研究方向包括：

1) 基于模型的制导与控制一体化设计

采用基于模型的方法,不仅有利于参数估计和状态辨识,还能在一定程度上起到解析冗余的效果,从而增强容错能力。此外,模型也是在线轨迹规划和任务重构的基础。

随着算力的提升,制导控制与轨迹规划之间的界限逐渐融合。轨迹规划从离线逐渐发展到在线规划,但一般在飞行中仅规划一次或有限次数,随后以规划的轨迹为基础进行制导控制,不具备每个控制周期均进行规划的条件。但这种“在线规划+轨迹跟踪”的处理方式同样面临着应对时变场景响应不及时的缺点,因此实时在线规划才是最具适应性的优化方法；但此种情况下在线规划已等同于制导控制。这需要算力更强的嵌入式计算平台和计算效率更高的算法,从而彻底解决因模型简化带来的最优性能损失的矛盾。

2) 容错制导技术

容错控制(FTC)属于研究得相当充分的领域,而容错制导(FTG)的研究尚处于起步阶段。FTC主要聚焦于保持飞行稳定,但仅仅保持飞行稳定并不能满足运载火箭的任务需求。在上升段时需要考虑克服引力满足入轨的能量需求,在着陆段时需要考虑充分减速的需求,这些均是FTG的技术范畴[232]。

FTG通过实时决策更换目标以尽可能减少任务损失,也需要以在线轨迹规划技术为基础。Song等[204-205]针对运载火箭上升段发动机推力下降故障,研究了一种基于状态触发目标函数的数值联立优化方法,根据故障状态自主规划新的目标轨道和飞行轨迹,从而提升有效载荷故障下留轨运行的可能性。对于可重复使用运载器,故障后提前返回也为FTG提供了新的可能性。

3) L2F技术

AI技术如何在重复使用运载器的飞行控制中发挥作用,还未取得重大突破,故本文未过多介绍与AI相关的方法。神经网络需要大量的训练样本,在真实的使用环境中提取样本更为有效。但重复使用飞行器制导与控制面临大量的模型不确定性和干扰随机性,存在地面试验样本集代表性弱、飞行试验子样少、采取数学建模与仿真手段获取的训练样本可信度低等缺点。另一个需要着重指出的是,采用离线训练的神经网络参与飞行控制,体现出一种数据触发的响应式开环控制特点；尽管样本中可能考虑了各种非标称条件,但失去了闭环反馈的特点,无论最优性还是适应性都难以保证。

正由于飞行中存在着设计人员未曾认识到或仿真出的工况,因此在飞行中学习才可能是AI能够真正发挥效果的场合。这项技术也被称作L2F技术[233],目前尚处于起步研究阶段。但AI技术也可以辅助基于模型的制导与控制,如对模型参数进行辨识,或提供优化计算的初值猜想。即AI技术只是替代或增强原有制导控制方法中的某一个环节,而不能全盘替代原有的方法。

4)基于物理模型的健康监测技术

运载器的多次复用和航班化运营,需要成熟可靠的健康监测技术,以提供类似于民用航班的地勤维护和日常检修服务。准确的故障诊断还可降低制导与控制的算法复杂度；并且,对健康状态的准确预示可以为在线决策提前提供信息。例如,造成火箭发动机推力下降的因素包括堵塞、泄漏、烧蚀或者效率下降等,不同的故障模式对任务重构的处理影响巨大。

健康监测离不开模型。通过偏微分方程、欧拉-拉格朗日方程组等建立“第一性原理”的物理模型,故障诊断的可信度更高。尽量避免采用基于参数的物理模型,这是因为如果没有考虑到合适的参数以表征故障状态,就有可能导致该故障发生时无法判别。这样的教训在长征火箭的飞行以及设计过程中均曾发生过,造成了严重的损失。模型自身可能是计算密集型的,需在保真度和计算效率之间进行权衡。

5)高保真度的地面仿真技术

学术性研究的技术成熟度为TRL1～TRL3级,而经过了原型验证(TRL6)至飞行验证(TRL9)的技术,将会被采纳参与正式航天任务。这其间的鸿沟需要在高保真的地面仿真环境中通过测试和改进以提升技术成熟度,推动从学术研究走向应用。

重复使用运载器面临跨域飞行和多种动力形式、多种飞行剖面的深度融合,单一场景的仿真技术无法满足要求,不同的仿真系统也很难做到无缝的衔接,有些条件也无法在地面环境下模拟,通过数学建模又面临诸多不确定性因素,这使得针对重复使用运载器的地面仿真比以往任何飞行器要更为困难。

高保真度的地面仿真环境能促进AI技术的应用,因为可以在此环境中提取更可信的训练样本。但这并不能改变本章节在3)中对AI技术用于重复使用飞行器的整体评价。