大动态干扰下基于光学图像的自主导航技术

李嘉兴,王大轶,鄂薇,葛东明

北京空间飞行器总体设计部,北京 100094

高超声速飞行器近些年来的发展方向是射程更远、精度更高[1],这无疑需要更高精度的导航能力。考虑到这种军事意义十分明显的飞行器要做到自主导航的迫切需求,探索适合于高超声速飞行器的自主导航技术成为了目前中国对该领域攻关研究的主要方向之一。天文导航是一种可靠的自主导航方法,在航天领域有很成熟的应用经验,将其与惯性敏感器进行组合导航可以达到长期稳定且高精度的导航效果。要将天文导航应用于高超声速飞行器仍处于研究阶段,主要受到了气动光学效应的影响。因为在飞行器高速飞行过程中,星敏感器窗口的大气被加热,流场发生巨大改变,产生激波、附面层等复杂流场,光线通过湍流后发生偏折,致使星图产生偏移、抖动和模糊等负面效果[1],严重降低导航能力。为了抑制气动光学效应,需要首先模拟在高超湍流成像条件下的天文导航图像,在此基础上研究图像复原算法。

目前针对气动光学效应的研究方法主要包括数值模拟和实验测量2种方法。数值模拟方法是利用几何光学、物理光学、统计光学等物理模型,在计算机中模拟光线穿过高速流场后的畸变波前,进而模拟出成像时的点扩散函数。现有的湍流数值模拟方法包括直接模拟法、大涡模拟法和雷诺平均法。直接模拟法能获得瞬态湍流但计算量巨大；雷诺平均法计算量小但无法模拟出瞬态湍流对光线的影响效果；大涡模拟法计算量居中且能够表达瞬时流场中的大涡结构,因此本文选用该方法进行气动光学效应仿真。近些年有不少数值仿真研究,例如Pond和Sutton[2]采用标准k-ε湍流模型对三维凸台周围的流场建立了数值仿真,利用相位差、斯特列尔比等参数对气动光学效应进行了评价。利用大涡模拟法研究气动光学效应已为主流,White和Visbal[3]对热壁面和冷壁面可压缩湍流边界层引起的航空光学像差进行了大涡模拟,还表明当壁面受热时光程差会增加。Kamel等[4]验证了一种带有壁面模型的大涡模拟方法的有效性。实验测量方法是直接测量光线穿过真实流场后的光程差数据,研究气流参数对图像模糊的影响机理。Gordeyev等[5]通过统计实验数据获得了非隔热壁面上边界层处波动密度场的预测模型。但这些针对气动光学效应的研究主要集中于数值仿真模型的建立、流场参数对光学成像指标的影响等方面,很少有面对气动光学影响下的图像复原研究。

近些年利用图像复原技术解决高超声速飞行器的气动光学效应问题受到了很高的重视。洪汉玉和张天序[6]在极大似然估计准则的基础上采用正则化方法复原红外图像,文中基于图像和湍流点扩展函数的梯度变化先验知识,提出了针对图像与点扩散函数特点的非线性各向异性正则化函数,使其估计模糊核与清晰图像时能自适应地平滑梯度。正则化复原方法近些年在国际上也备受关注,学者们利用不同的先验模型设计正则函数。大多数文献针对图像和梯度的分布特点设计模型,Fergus等[7]提出基于变分贝叶斯的图像盲复原方法,Krishnan和Fergus[8]发现了图像梯度的重尾分布并用超拉普拉斯分布来拟合。Li等[9]引入了分裂布雷格曼迭代法用于解决非凸优化模型。Ohkoshi等[10]提出结合全变差模型和Shock滤波器的盲复原算法。Zhao等[11]利用Lp范数拟合车牌图像的分布特征,模糊图像中同时考虑了离焦与运动模糊问题,并用交替方向乘子(ADMM)算法求解复原模型的最优值。Sun等[12]利用迭代支持检测方法精细化模糊核,以降低图像噪声对模糊核估计结果的精度影响。Pan等[13]提出基于暗通道稀疏先验知识的盲复原算法。而根据低秩先验原理,Ma等[14]设计了基于加权核范数正则化和全变差正则化的复原模型,前者能够降低由相似局部图像堆叠而成的矩阵的秩,进而约束去噪与模糊复原过程。以上这些图像模糊复原方法大多是为自然图像设计,而为了解决气动光学大动态对天文导航图像影响,需要针对这种图像的特点进行专门的复原模型设计,与气动光学的研究成果相结合。

模糊核的先验信息有助于获得更接近真实值的模糊核估计结果[15]。文献[16]为解决气动光学效应专门设计了星图复原算法,利用从图像中提取的先验模糊核进行非盲复原。但该方法无法适应先验模糊核提取精度低或无先验信息等情况。为了解决这一问题,本文提出一种新的改进算法,在对气动光学影响下星图特点研究的基础上,把先验模糊核与盲复原方法相结合,设计了新的正则化图像复原模型,既具备了盲复原算法可以在未知模糊核情形下的复原能力,又具备了非盲复原算法对先验模糊核中图像信息的利用能力,提高算法应用时的鲁棒性和复原精度。

1 高超湍流场的运动星图模糊核

基于高超湍流的大涡模拟(LES)流场数据,利用几何光学和物理光学,湍流场影响下的星图模糊核,引入随机运动模糊,建立具有气动光学效应和运动模糊的高超湍流的运动模糊核。

1.1 高超湍流的大涡模拟

星光经过激波、湍流边界层、弹体冷却层等之后,光学窗口外复杂高速流场产生的气动光学效应使星敏感器接收的图像存在严重的偏移、抖动和模糊。由激波引起的稳定偏折可由文献[1]中的经验公式计算,而本文只重点研究湍流模糊与运动模糊问题。

为了尽可能准确地揭示高超湍流场中星光光线传播的特性,使用大涡模型对湍流流场进行模拟,其流场密度分布如图1所示。

1.2 湍流影响的星图模拟

基于上述大涡流场模拟结果,利用物理光学原理,采用光线追击法,计算平行光穿过流场后的光程差,如图2所示。根据文献[1]中的方法,由光程差进一步计算气动光学效应造成的高超湍流模糊核hH。

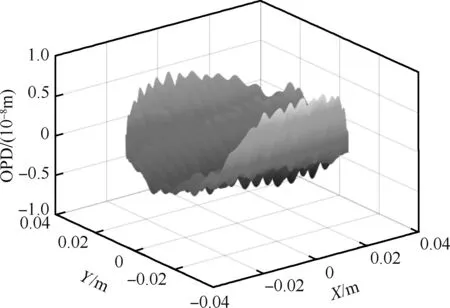
图2 光程差

当高超声速飞行器飞行时受到气流扰动和机体振动导致光轴发生抖动,造成的运动模糊核记为hM,将其与高超湍流模糊核卷积即可得到高超湍流场运动模糊核h,如式(1)所示,卷积结果如图3所示。

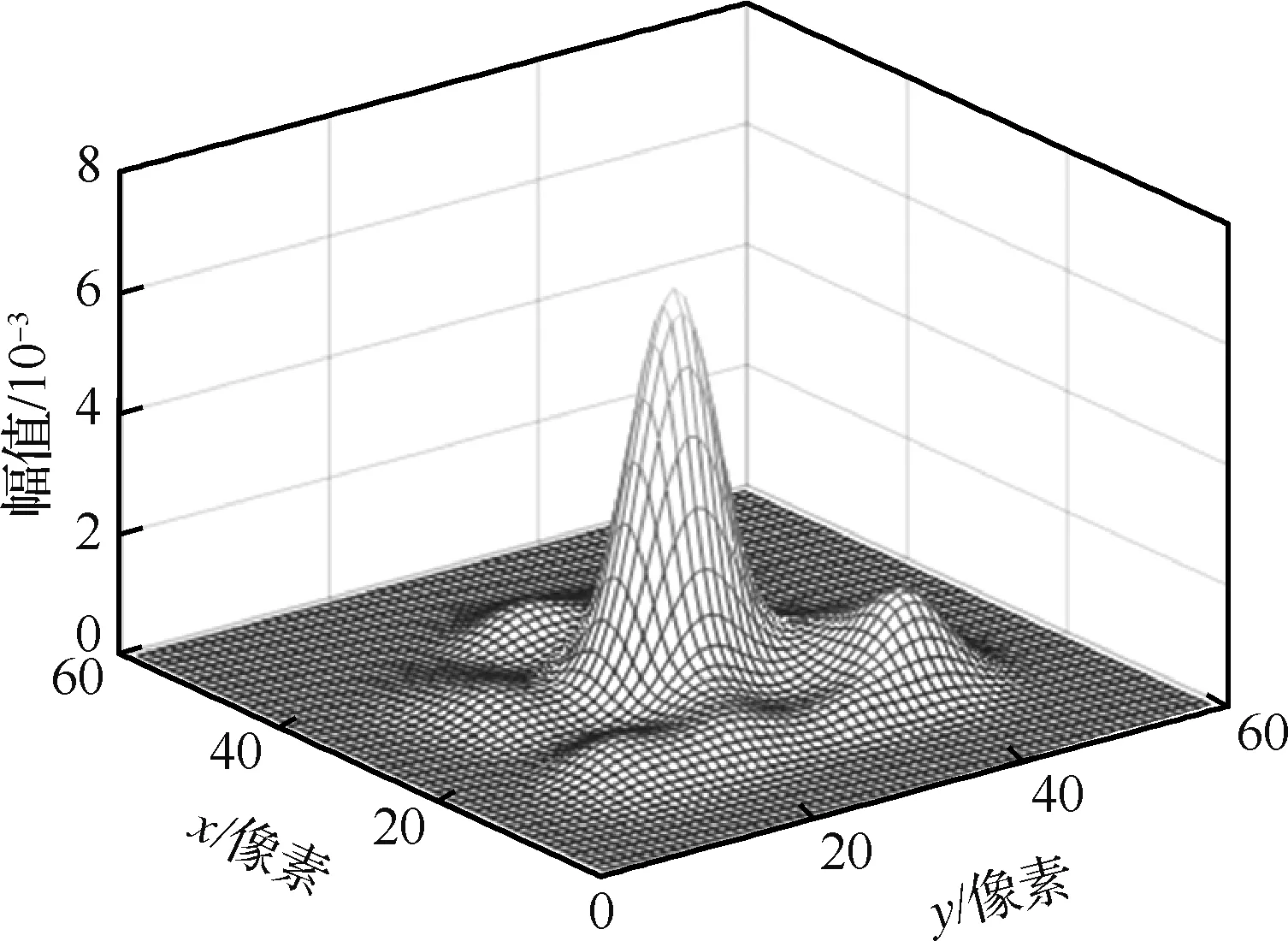
图3 高超湍流场运动模糊核

h=hH⊗hM

(1)

式中：⊗为空间卷积运算,根据湍流冻结理论,在短曝光前提下可将模糊退化过程表示为目标图像与模糊核的卷积过程,同时考虑噪声:

g(x,y)=f(x,y)⊗h(x,y)+n(x,y)

(2)

式中：g(x,y)为退化图像；f(x,y)为清晰的目标图像；n(x,y)为加性噪声。为方便表示,下文将写作g,f,h,n。

2 先验模糊核提取与分析

图像复原是模拟模糊图像过程的逆过程,在实际导航过程中,需要从模糊图像当中提取有用信息,利用复原算法获得清晰图像。区别于自然图像当中利用盲复原算法估计模糊核,基于天文导航图像的独有特点,可以先从星图当中提取模糊核的先验信息来指导复原过程,称之为先验模糊核。

2.1 先验模糊核提取

天文图像的模糊核提取与光学系统点扩散函数测量问题中的点脉冲法十分相近,星图中每颗星的图像与模糊核非常相近,借助这一特性从模糊星图中提取模糊核的先验信息,为复原提供依据。但在气动光学作用下,需解决模糊核重叠、图像边界处不完整及成像噪声等问题。

假设星图中有M颗星,第m颗星的坐标是(xm,ym),(m=1,2,…,M),能量为Im的星点图像为Imδ(x-xm,y-ym),其中δ(x,y)为脉冲函数,则原始星图可表示为

(3)

经过点扩散函数h的退化,并加入噪声后的退化图像可表示为

xm,y-ym)+G(μn,σn)

(4)

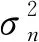
假设1阈值分割阶段可以估计出准确的噪声均值。

当假设1成立时,在退化图像中去除噪声均值,即g-μn后,边界延拓L/2个像素,以(xm,ym)为中心,提取L×L的图像为

Ωm(x,y)=Imh(x,y)+G(0,σn)+

(5)

式中：L为估计模糊核的支持域边长,单位为像素个数；Δxmm′=xm′-xm；Δymm′=ym′-ym；D(sm,sm′)为m星到m′星之间的距离。

由式(5)知,Ωm(x,y)中包含m星对应的点扩散函数h、零均值噪声以及重叠的其他星的干扰能量,将Ωm(x,y)写为极坐标形式Ωm(r,φ),按照文献[16]中的算法提取出先验模糊核。

假设 2利用文献[16]的算法成功剔除了m星与其他星的模糊重叠区域。

加权融合后的模糊核表示为

(6)

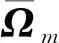
(7)

(8)

利用文献[16]中的先验模糊核提取算法,能够剔除相邻星之间图像的重叠区域,从而避免了大扰动条件下模糊核重叠的问题。对图像进行边界延拓可以使图像边界处模糊核不完整时也能正常提取有用信息。

2.2 先验模糊核特性分析

式(5)在满足假设2的条件下,可改写为

(9)

期望和方差为

(10)

(11)

将式(7)、式(9)代入式(6)可得

(12)

则期望和方差为

E(hp(r,φ))=h(r,φ)

(13)

(14)

在满足假设1和假设2的条件下,式(13)表明模糊核先验估计hp是退化真实模糊核h的无偏估计。且由式(14)可以看出融合后的hp方差一定不会大于融合之前,而且所利用的图像信息越多、能量越丰富,方差越小,去噪效果越强。下面定性描述hp与h的差异,为用于表征先验模糊核的可信任度。

由式(14)得到hp每点处的方差为

(15)

为描述hp与h的误差,采用二者差值的均方误差

(16)

将式(15)代入式(16)可得

(17)

同时,均方误差亦可表示为

(18)

(19)

将式(19)代入式(18)可得

(20)

(21)

hp-h为融合后的噪声,与h相独立,则

(22)

式中:

(23)

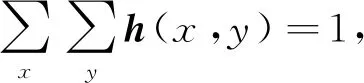
(24)

(25)

将式(17)、式(25)代入式(20)可得hp与h相似度的估计为

(26)

在估计相似度时,只需要先验模糊核hp和噪声方差估计值这些已知量,不需要实际模糊核h。因此式(26)的估计方法适用于在未知h的前提下盲复原模糊星图时,衡量所提取的先验模糊核的可信任程度,为复原算法在利用hp时提供参数设计依据。

3 高超星图正则化半盲复原

3.1 半盲复原模型设计

由式(2)所示的图像退化模型可知,图像盲复原的过程用数学可以表示成为求解未知量f与h使得后验概率P(f,h|g)取得最大值,即可表示为如下最大后验概率问题:

(27)

式中:f*表示清晰图像的最优估计;h*表示模糊核的最优估计。根据贝叶斯定理,后验概率P(f,h|g)可以转化为

(28)

由于在图像复原过程中模糊图像g为已知量,因此式(28)中的分母是一个固定的归一化常数,可以忽略,于是可以得到

P(f|g,h)∝P(g|f,h)P(f)P(h)

(29)

将式(29)代入式(27)可得

(30)

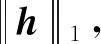
(31)

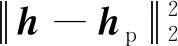
综上,本章提出的高超星图正则化半盲复原模型设计为

(32)

3.2 最优化求解

为了使模糊核估计更精确,总体求解思路采用文献[7]中提出的多尺度框架策略,从分辨率由低到高进行逐层复原,特别针对严重模糊的图像,能够有效避免陷入局部最优。式(32)是一个非凸优化问题,需要交替迭代g与f进行更新。下面为该算法的具体过程,记为算法 1。

3.2.1 目标图像估计

在更新目标图像f的阶段,固定上一次迭代得到的h,则f的子问题可转化为如下最优化问题:

(33)

式中：Hf=h⊗f。

式(33)为Lp范数的优化问题,采用半二次惩罚技术,引入辅助变量a=f,b1=δx⊗f,b2=δy⊗f,得到新的目标函数为

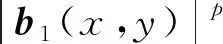
(34)

交替计算f与辅助变量。式中：δx和δy分别表示水平和垂直一阶差分算子,δx⊗f和δy⊗f简写为δxf和δyf。惩罚参数α越大时式(34)的解越接近式(33)的解,最终f可由式(35)计算:

(35)

(36)

同时,辅助变量的子问题表示为

(37)

式中：w∈{a,b1,b2}；v∈{f,δxf,δyf}。采用文献[8]给出的LUT(Look up Table)算法快速求解。

3.2.2 模糊核估计

在更新模糊核h的阶段,固定上一次迭代得到的f,则h的子问题可转化为如下最优化问题:

(38)

式中：Fh=f⊗h。

式(38)为L1范数的优化问题,利用分裂Bregman迭代来求解。采用半二次惩罚技术,引入辅助变量c=h,式(38)可改写为迭代框架

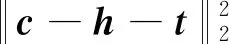
(39)

t:=t+h-c

(40)

固定c、t,更新h的方法为

(41)

利用式(41)更新模糊核后对其进行归一化

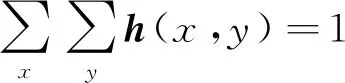
(42)

并为了提高抗噪鲁棒性,施加动态阈值约束

(43)

式中：δh表示阈值参数。固定h、t,利用快速收缩算法求解c的最优解:

(44)

综上,利用算法 1复原图像的过程如图4所示。先利用经预处理后的模糊图像进行目标图像估计,再利用先验模糊核和相似度进行模糊核估计,这一过程作为一个循环。每次循环结束前将参数α扩大αInc倍,但不超过αMax,一共进行N次循环。再将算法 1代入文献[17]中的金字塔算法,来提高大尺度模糊时算法的鲁棒性。

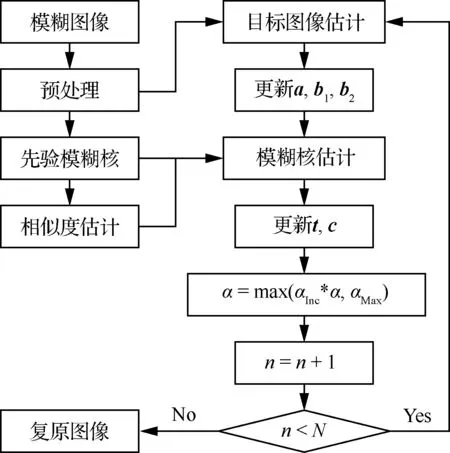
图4 算法1流程图

4 算法收敛性验证

改进的半盲复原算法中,目标图像估计阶段,hp给定,f的子问题为凸优化,其他参数均由查表法获得最优值,收敛性不必证明。因此只有计算h时的L1约束项通过Bregman分裂法进行近似,因此下文将证明其收敛性。式(38)的递推式可写为

(45)

式(45)为L1范数的优化问题,利用分裂Bregman迭代来求解。采用半二次惩罚技术,引入辅助变量c=h,式(45)转化为无约束分裂形式

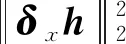
(46)

式(46)可改写为迭代框架

(47)

(48)

tn+1=tn+(hn+1-cn+1)

(49)

式(47)～式(49)子问题是凸性可微分的,可得一阶最优条件为

0=FT(Fhn+1-g)+θη1hn+1-θη1hp+

(50)

0=rn+1+2β(cn+1-hn+1-tn)

(51)

tn+1=tn+(hn+1-cn+1)

(52)

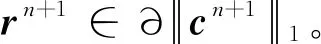
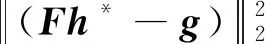
(53)

(54)

并且此解是唯一解。

证明：因为式(46)存在至少一个解h*,其一阶最优条件满足:

(55)

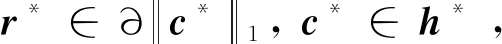
0=FT(Fh*-g)+θη1h*-θη1hp+β(1-θ)×

(56)

0=r*+2β(c*-h*-t*)

(57)

t*=t*+(h*-c*)

(58)

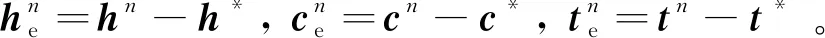
(59)

(60)

(61)

(62)

将式(61)与式(62)相加,得到

(63)

用式(52)减去式(58),可得到

(64)

对式(64)的等号两边求平方,得到

(65)

(66)

将式(66)代入式(63)中,得到

(67)

(68)

(69)

(70)

对式(70)的等号两边分别从0到N进行求和运算,可以得到

(71)

式(71)中的各个项都是非负性的,于是有

(72)

假设β,η1,η2,η3>0, 0<θ<1,并且使得N趋近于无穷,对于不等式(72)得到结论

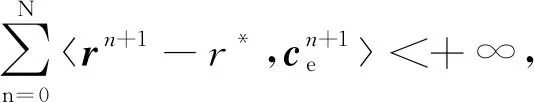
因此可以得到

(73)

(74)

(75)

(76)

(77)

(78)

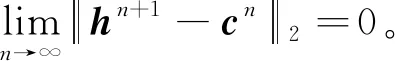
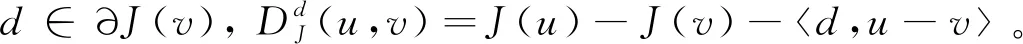
(79)

(80)

hn-h*=0

(81)

(82)

hn-h*=0

(83)

(84)

(85)

综合式(80)～式(85),可得

(86)

由式(55),可得

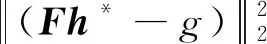
(87)

再结合式(82),即可证明收敛至h*,下面证明解得唯一性：定义

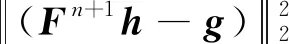
(88)

E(hni)>ζE(h*)+(1-ζ)E(hni)≥E(ζh*+

(1-ζ)hni)=E(v)≥min{E(h):

(89)

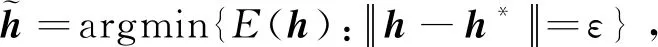
(90)

存在矛盾,因此h*是唯一最优解。

5 仿真验证

5.1 仿真条件

5.2 仿真结果

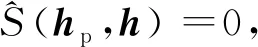
表1 不同算法的平均PSNR对比

从图5、图6中可以直观地得到以下对比结果。CLSF是一种非盲复原算法,因此直接使用先验模糊核做复原,但这种方法对模糊核估计准确度的要求较高,当模糊核不够准确时复原图像精度较低,没有先验模糊核时更无法进行复原。Krishna等[18]的算法使用L1先验,对模糊核和图像的平滑度略高,可以抑制绝大多数噪声,但模糊核的形状比较窄,同时复原的星点较粗,能量不够集中,出现了相邻星互相重叠的现象,有时难以区分。Pan和Su[19]的算法使用L0先验,对图像表征的稀疏程度更高,虽然复原的图像能量更集中,但过度保留了图像和模糊核中梯度的分布,使复原图像和模糊核中依然存在大量高频噪声,可能会对星图识别造成干扰。文献[16]是采用了Lp先验模型的非盲复原方法,平滑程度介于L1和L0之间,在抑制噪声的同时也使得目标星点能量更集中。相比文献[16]直接使用先验模糊核进行复原,算法 2加入了模糊核估计项,是一个盲复原方法,由于其仅依靠传统的模糊核估计项,得到的模糊核精度依然不高,但同样采用了Lp先验模型使得其复原效果低于文献[16]又强于文献[18-19]。在先验模糊核的帮助下,算法 1估计出的模糊核与实际模糊核相差不多,并且由于其具备盲复原的功能,不完全依赖先验模糊核,能够在复原过程中对模糊核进行调整,因此其复原效果更佳。

图5 不同算法的模糊核对比

图6 不同算法的复原星图对比

星图复原后提取质心坐标,与真实坐标进行对比,若二者相差小于2个像素就认为提取正确,并统计正确识别的个数占总个数的识别正确率,如表2所示。造成提取失败的因素可能有复原后噪声被放大,被错误的提取出来；模糊程度较大的星没有正确复原,没有被提取出来；复原后的质心比原始质心偏移较大；两颗相邻的星模糊后重叠在一起,复原时没有将二者分离开等等。将正确识别的星点坐标与真实坐标进行对比,统计二者的平均误差角距如表2所示。从表中的数据分析算法的复原能力,可以得到与前文相似的结论。同时发现文献[18-19]和算法 2等盲复原方法质心提取偏差较大的现象,是因为在缺乏先验模糊核辅助时估计的模糊核不够准确,没有拟合出模糊核中的多峰结构,致使复原出来的星点图像依然存在多峰结构,除主峰以外的次峰会严重影响星点质心的计算精度。

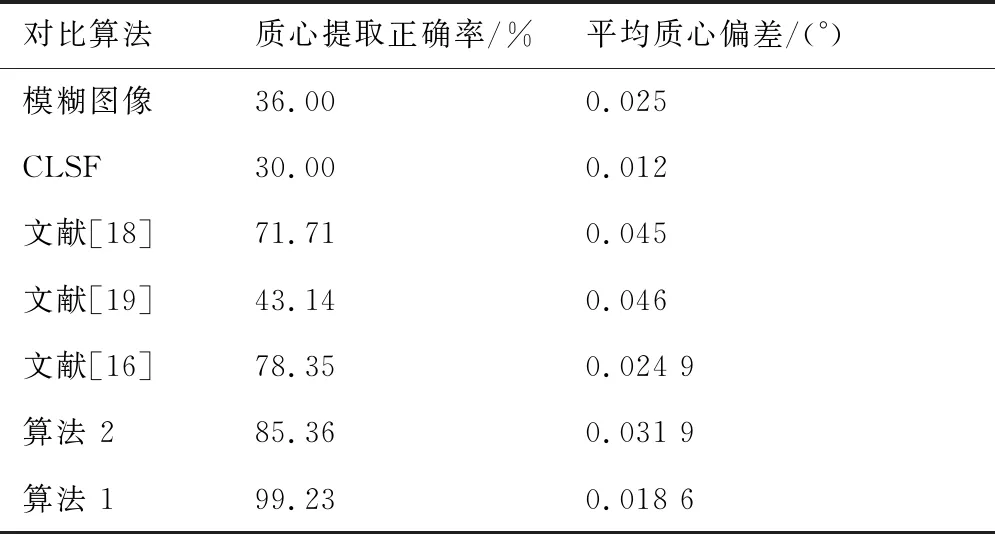
表2 不同算法的质心提取精度对比

采用文献[20]给出的误差率作为评价模糊核的估计准确度,对不同算法统计积累误差率绘制曲线如图7所示,图中曲线越高说明模糊核估计得越准确。从图中可以看出算法 1的模糊核估计准确度更高。

图7 不同方法的积累误差率

在6马赫的飞行速度下,改变飞行高度,利用算法 1复原后的质心偏移曲线如图8所示,可以看出随着飞行高度的提升,大气密度随指数降低,高超湍流带来的模糊强度也逐渐降低,因此对质心偏移的影响也逐渐变小。可以看出若想降低气动光学效应对天文导航精度的影响,除了图像复原之外,还可以提升飞行高度。

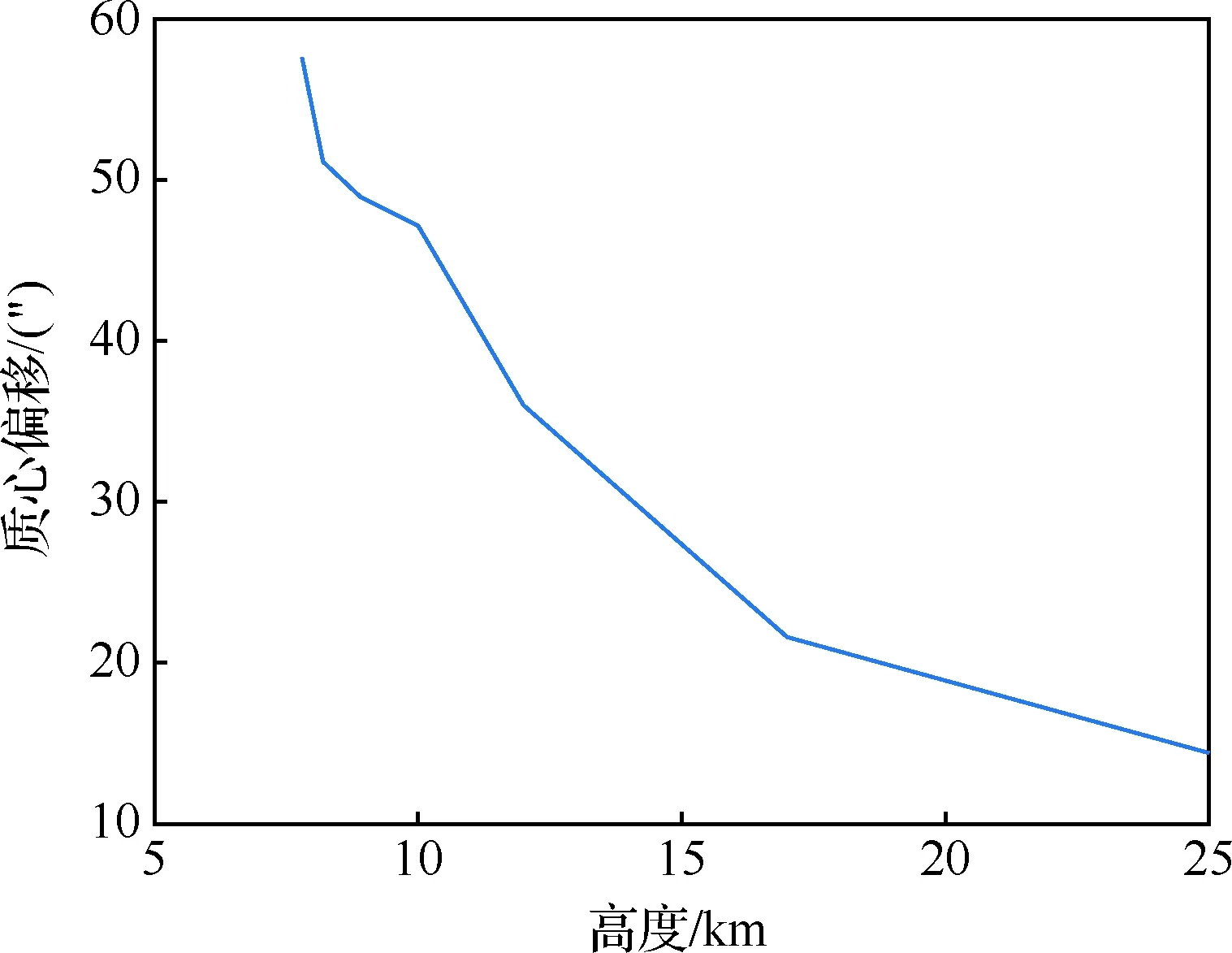
图8 质心偏移随飞行高度变化

综合上述对比分析,本文提出的半盲复原算法相较于其他对比算法,对模糊核的估计更加准确,针对高超湍流模糊星图的复原效果更好,用于星点质心提取的正确率和精度更高。本文的两种算法相互对比,带有模糊核先验项的算法 1比算法 2效果更好,说明在先验模糊核的作用之下,估计出的模糊核准确度比完全盲复原时要更高,从而使得复原精度也更高。

6 结 论

针对高超声速飞行器在平流层中使用天文导航进行自主导航过程中,星图受气动光学效应及运动模糊干扰的关键问题,深入研究了高超星图的复原方法,抑制气动光学效应给天文导航带来的负面影响。

1) 本文在盲复原算法的基础上,利用先验模糊核提供的信息引导模糊核估计的过程,形成了半盲复原模型。

2) 设计了针对复原模型的优化求解算法,交替估计模糊核与清晰图像,并验证了该方法的可收敛性。

3) 通过实验发现提高了模糊核估计的精度,以及复原图像的精度,最终平均PSNR可达到36.97,质心提取正确率达到99.23%,质心偏差缩小至0.018 6°。

因此该算法可进一步提高高超声速飞行器的天文导航精度,提升大动态下光学自主导航能力。