多滑翔飞行器时间协同轨迹快速规划

刘哲,陆浩然,郑伟,*,闻国光,王奕迪,周祥

1. 国防科技大学 空天科学学院,长沙 410073

2. 北京宇航系统工程研究所,北京 100076

3. 北京交通大学 理学院,北京 100093

高超声速滑翔飞行器是一种在临近空间飞行,最大速度可达马赫数20以上的升力式飞行器,具有速度快、侧向运动能力强、精度高、强突防的特点。然而随着反导武器防御系统的不断完善和发展,单个飞行器的生存能力下降,传统的多弹同时饱和攻击方式突防能力有限。因此,高超声速飞行器集群中的个体可通过精确协同控制再入总时间及终端状态的方式,多角度、多批次抵近目标,从而实现“探测-打击-评估”一体化协同再入,有效提升集群的综合效能。

相关学者从2005年起开始对多弹协同算法的研究。文献[1]最早设计了固定总时间约束下的单弹最优制导律(ITCG),实现了多弹同时到达目标点；文献[2-3]分别提出了“领弹-从弹”及双层协同架构,后续的多弹协同末制导方法多基于这两种架构,协同方式主要集中在时间协同。近年来,文献[4]首先论证了高超声速飞行器与常规导弹协同的可行性,而后对于高超集群协同轨迹规划与制导的研究逐渐兴起。

相比于多弹、多无人机协同,滑翔飞行器集群为欠驱动系统,控制能力有限,再入环境复杂,多弹协同方法无法直接应用,因此多采用“标准轨迹法[5]”“预测校正法[6-9]”或优化方法实现多滑翔飞行器时间协同。文献[5-6]通过调节航向角误差走廊宽度的方式改变侧向运动幅度,间接控制再入总时间；文献[6]在文献[5]的基础上,采用神经网络拟合了航向角误差走廊边界与到达时间的关系,动态改变走廊边界进行时间调节。文献[7-8]基于预测校正方法,直接迭代调整控制量剖面以实现时间控制；文献[9]利用模型预测静态规划(MPSP)算法替代了预测校正的迭代过程；文献[10-11]将“领-从”模式及ITCG方法应用到了多高超声速飞行器的末制导段。上述方法存在的问题在于: ① 难以获取再入总时间的可调范围并确定合理的协同时间; ② 标准轨迹方法中航向角误差走廊的增大会导致终端误差的增大; ③ 预 测校正方法一般只能满足终端位置与协同时间需求,很难同时满足终端角度约束,迭代求解的收敛性受初值影响较大。

为满足终端位置与角度约束,伪谱法等优化方法将问题离散化后求解,但计算用时较长,且同时满足协同时间约束的文献相对较少。MPSP算法通过解整个时间段的协态向量来更新控制变量解,不需要直接对非线性动力学模型采用线性化假设,计算效率、数值精度高,但大多需要对控制量进行预设计以获取初始猜想解[12-13]。

近年来,序列凸化算法以其快速收敛性得到了广泛应用[14-25]。文献[14]利用序列二阶锥规划(SOCP)求解了再入飞行器的最速下降轨迹,但未涉及给定协同时间约束下的规划方法；文献[15]直接将协同时间加入约束中,采用平面相对运动学模型求解,未考虑实际的动力学环境；文献[16-17]分别通过减弱模型非线性,避免凸化处理的方式提高算法收敛性。此外,相关学者通过在求解过程中调整信赖域半径的方式加快收敛速度,主要包括将信赖域作为“硬约束”与“软约束”两类[18-22]。文献[18-20]将信赖域作为硬性约束加入到求解模型中,并根据各次迭代过程的线性化误差等指标调整信赖域半径,但求解给定协同时间下的规划问题时,常出现存在多条最优轨迹的情况,导致解会在两条最优轨迹间不断振荡,序列迭代算法难以收敛；文献[21-22]分别将信赖域及线性化误差加入罚函数中,从而在保证线性化误差尽可能小的同时加快收敛速度,但此类方法在处理本文问题时会使得罚函数中惩罚项过多,各项的系数大小难以确定,不利于实际应用。同时,不合适的信赖域惩罚项更新策略会导致算法收敛性下降,甚至搜索不到最优解。

针对以上问题,本文首先给出了“探测-打击-评估”一体化模式下集群再入的协同规划方案与数学模型,进一步将协同轨迹规划问题转化为3个子问题进行求解,即：飞行器再入总时间可调范围的快速获取、期望协同时间的确定、给定协同时间约束下的轨迹规划。将飞行路径角初值剖面定义为二次曲线,并将终端经纬度偏差、总时间偏差以及飞行路径角相对于预设剖面的偏离程度加入罚函数,提高了问题的可解性。提出了一种罚函数与信赖域系数自适应策略,在求解过程中不断调整目标函数中时间项所占权重,并根据罚函数值的变化收缩信赖域,从而在飞行路径角平滑剖面附近逐步搜索得到最优解,提高了序列迭代算法求解目标函数中含时间项问题的收敛性。实现了不同再入任务下多滑翔飞行器时间协同轨迹的快速规划,并与伪谱法及MPSP算法求解结果进行了对比。

1 集群时间协同再入问题描述

1.1 集群时间协同再入策略

为实现“探测-打击-评估”一体化协同再入,采用两种时间协同方案： ① 不同起始点的多个集群确定协同再入时间,同时到达目标点,实现多方向饱和攻击； ② 单个集群内部各飞行器通过采取不同轨迹形式控制再入时间,从而使同一集群内部成员多批次到达目标点。其中前序飞行器负责探测,并将态势信息向后传递,后序飞行器负责攻击及效果评估,实现时域协同。图1 给出了“探测-打击-评估”一体化集群协同再入模式的示意图。

图1 “探测-打击-评估”一体化协同再入

两种协同再入方式首先均需快速确定集群内部各飞行器的再入总时间范围,确定协同到达时间后对各子飞行器轨迹进行精确的时间控制。可见,高超声速集群滑翔段时间协同对轨迹解算的快速性有较高要求,是一种新的再入轨迹规划问题,即在满足式(1)、式(6)、式(12)、式(13)的约束条件下,优化得到再入总时间范围,进而进行固定期望协同时间约束下的轨迹规划。

1.2 飞行器数学模型

对于高超声速滑翔飞行器再入集群中的第i个成员,其以能量为自变量的无量纲三自由度动力学模型为

(1)

(2)

式中：ρ为大气密度；Sref为参考面积；m为飞行器质量；CL和CD分别为升力系数、阻力系数,其值由当前时刻的攻角α及马赫数Ma二维插值得到。模型的自变量为无量纲化后的能量：

e=1/r-V2/2

(3)

则在地心距为r处,飞行器的速度为

(4)

再入过程中控制量为攻角α和倾侧角σ,攻角剖面一般设置为固定形式,则再入轨迹可由倾侧角剖面σ(e)唯一确定。

1.3 约束条件

1.3.1 控制量约束

在进行滑翔段轨迹规划时,采用“固定攻角剖面+可控制倾侧角剖面”的控制方式。根据工程经验,攻角一般定义为线性剖面的形式：

(5)

式中：αmax、αmax L/D分别为滑翔飞行器所允许的最大攻角及最大升阻比所对应的攻角；V1、V2为攻角剖面转折点对应的速度值。本文限制飞行过程中升力方向一直向上,则倾侧角σ的允许变化范围可以表示为

σmin≤|σ|≤σmax

(6)

为了避免控制量振荡对于轨迹求解收敛性的影响,采用文献[14]中的控制量选取方式,转化后的新控制量可分解为向量形式u=[u1,u2]：

u1=cosσ,u2=sinσ

(7)

则仅需对控制量的分量进行约束：

(u1)min≤u1≤(u1)max

(8)

由于分量u1为标量,因此式(8)满足凸约束条件。此外控制量还需满足：

(9)

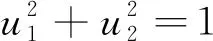
1.3.2 过程约束

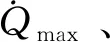
(10)

式中：KQ=9.43×10-5,标准大气密度ρ可展开为

ρ=ρ0e-h/hs

(11)

式中:hs为基准高度。

h≥hQ(e),h≥hq(e),h≥hn(e)

(12)

1.3.3 终端约束

高超声速飞行器滑翔段结束后,为使飞行器能够充分利用自身机动能力顺利到达预定目标点,需要对滑翔段结束点的位置、速度等状态量进行约束,则当飞行器到达终端能量状态ef时,终端状态量需满足：

(13)

2 考虑协同时间约束的改进序列凸化方法

由于目前相对缺少对多滑翔飞行器协同轨迹规划算法的研究,协同时间约束难以满足,因此本文针对实现“探测-打击-评估”一体化协同再入的任务需求,提出了协同到达时间约束下的轨迹规划方法。首先,根据两种集群时间协同再入形式,分别提出了协同时间的确定策略。而后利用序列凸化算法快速解算协同轨迹。图2给出了时间协同轨迹规划的具体流程。

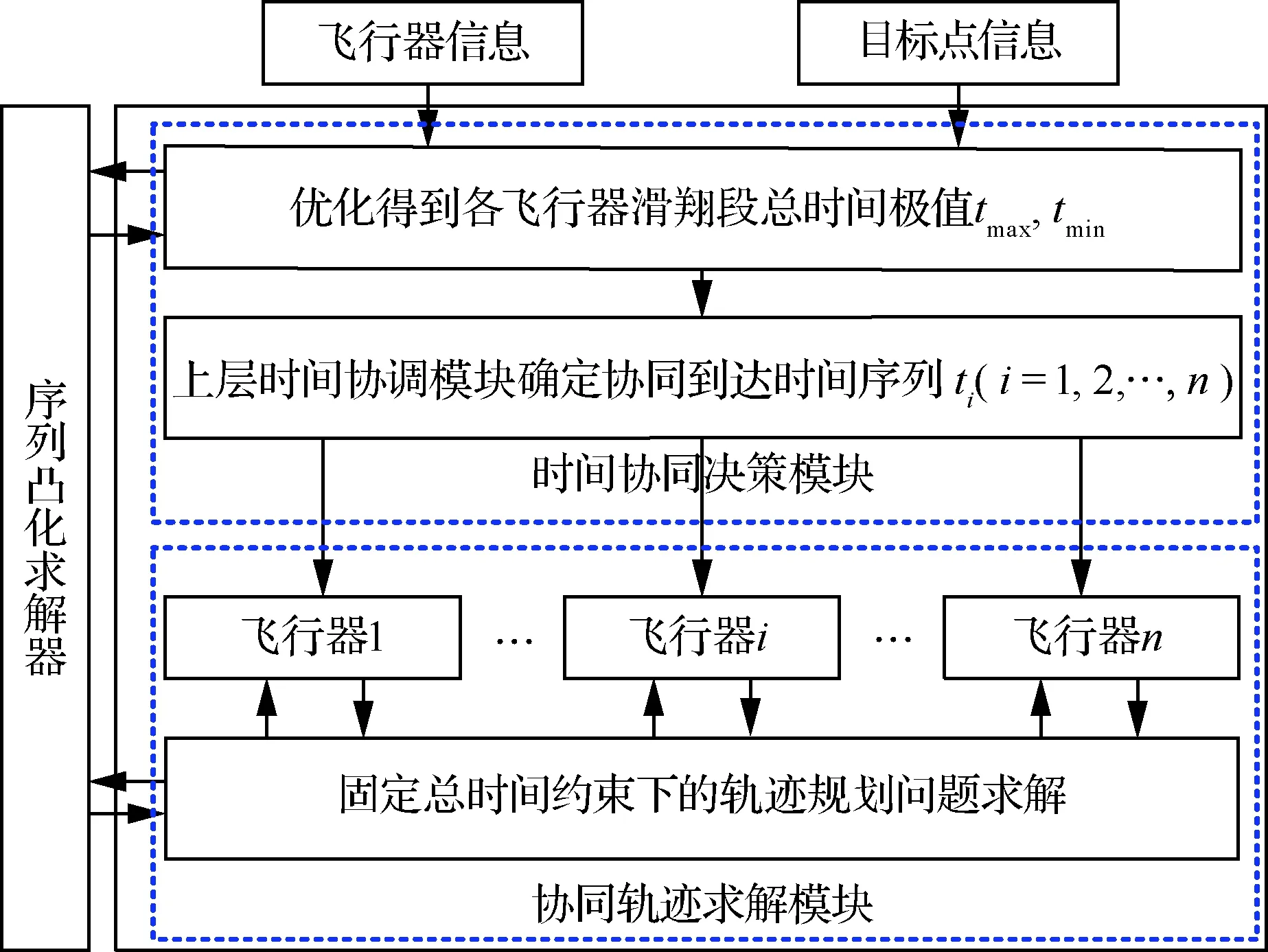
图2 时间协同轨迹规划流程

2.1 时间协同轨迹规划问题

2.1.1 协同时间的确定策略

首先,通过时间协同决策模块综合飞行器及任务目标点的状态信息,利用序列凸化算法快速优化得到各飞行器滑翔段的总时间可调范围,进而由上层时间协调模块根据任务场景确定协同到达时间或到达时间序列。接下来,将协同时间下发至各飞行器,各飞行器分别进行固定期望协同时间约束下的轨迹规划问题求解。不同任务场景下的协同时间确定策略为

1) 多个飞行器同起点同时开始滑翔,序列多波次到达同一目标点。

步骤1利用序列凸化算法快速解算该起点到目标点的滑翔最长时间tmax以及最短时间tmin。

步骤2按集群内部飞行器个数确定到达时间间隔Δt,生成到达时间序列ti：

(14)

式中：n为集群中飞行器总个数；i为飞行器编号,i=1,2,…,n-1。

步骤3将协调时间指令ti下发至各个飞行器,各子飞行器分别进行固定滑翔段总时间约束下的轨迹规划。

2) 多个飞行器不同起始点同时开始滑翔,同一时间到达同一目标点。

步骤1分别优化得到各个起点到终端目标点的滑翔最长时间tmax,i以及最短时间tmin,i。

步骤2多飞行器的协同到达时间t可依据式(15)确定,以使得多飞行器同时到达目标点。

t∈[tmin,1,tmax,1]∩…∩[tmin,i,tmax,i]

(15)

在本文算例中,不同起点的飞行器滑翔段协同时间t按式(16)计算：

(16)

步骤3将协同时间指令下发至各子飞行器,各子飞行器进行固定滑翔段总时间约束下的轨迹协同规划。

2.1.2 协同时间约束下的轨迹优化模型

针对以上任务场景需求,将协同轨迹规划问题转化为2个子优化问题,即P1：再入滑翔段飞行最长、最短总时间优化问题；P2：固定总时间约束下的轨迹规划问题。结合各类约束条件,滑翔段轨迹优化问题求解模型可以被初步描述为

(17)

式中：tf为滑翔段终端时间；δtf为终端时间相对于期望协同到达时间的偏差；R0为地球半径。

2.2 考虑时间约束的预设剖面设计

将再入过程分为初始下降段及滑翔段,初始下降段倾侧角设置为常值。定义剩余航程s为飞行器当前位置到目标点连线在地球表面投影的大圆弧长度,其表达式为

s=R0arccos[sinφsinφf+cosφcosφfcos(λf-λ)]

(18)

对时间求导可得

(19)

式中：Δψ为航向角误差。由e=1/r-V2/2可得

(20)

则无量纲化剩余航程s相对于能量e的变化率为

(21)

由式(21)可知,飞行器在纵向平面内航程s的变化主要由飞行路径角γ、地心距r和阻力加速度D所决定。由于以能量为离散自变量进行轨迹设计,各个离散点处e的是固定的,且r近似为1,因此速度v和阻力加速度D的变化形式相对固定,s的大小主要取决于飞行路径角γ的剖面形式[23]。仿真实验表明,极值总时间或满足期望时间约束对应的轨迹有时并不唯一,为提高算法收敛性,并且使滑翔段轨迹规划结果尽量平滑,将飞行路径角γ的初值剖面定义为二次曲线的形式：

(22)

式中：γ0、γf为初始点及目标点处的飞行路径角,则当中间能量状态处的飞行路径角γmid确定后,即可确定飞行路径角全程剖面,积分式(21)得到总航程s。迭代求取γmid,当式(23)成立时,可认为飞行路径角初值剖面满足终端航程要求。

(23)

2.3 时间协同轨迹优化问题的凸化处理

为应用SOCP算法,需对目标函数中的时间项进行凸化处理。此外,将P0中的连续非线性动力学方程线性化,转化为离散型有限维最优控制问题进行求解。

2.3.1 时间项的凸化

将飞行时间转化为模型状态量的线性表达式,再入段末端时刻tf可表示为

(24)

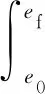
(25)

将式(2)及的表达式代入式(25)可得

(26)

式中：ρr为大气密度ρ相对于地心距r的导数;Tr为T相对于地心距r的导数。

2.3.2 动力学约束的凸化

按式(7)重新选取控制量后,系统动力学模型可整理为线性的凸约束形式：

(27)

式中:w(x,e)为与地球旋转有关的项,

(28)

(29)

(30)

2.3.3 问题的离散化

轨迹规划问题为连续型无穷维非线性规划问题,求解时需要对其进行离散化。本文以能量为自变量,采用梯形离散化方法,在滑翔段能量变化区间[e0,ef]内取均匀分布的N+1个离散点{e0,e1,e2,…,eN},相邻两个离散点的距离Δe满足:

Δe=(ef-e0)/N

(31)

则各个离散点对应的能量ei为

ei=e0+i·Δei=0,1,…,N

(32)

离散后的状态量和控制量可分别表示为(x0,x1,…,xN)和{u0,u1,…,uN}。第i个离散点处控制量为ui=[cosσi,sinσi],第i个离散点处附近对应的动力学约束可以被线性化为

(Aixi+Βiui+bi)]=0i=1,2,…,N

(33)

(34)

式中：ri为第i个离散点处的地心距;Tri,τi为线性化系数,由第k-1次序列迭代的解代入得到。

2.4 固定时间约束下的序列凸化算法

若仅以式(34)作为目标函数,则会导致控制量求解结果不满足约束条件[14],因此引入复合型目标函数,将终端经纬度偏差及时间项加入罚函数,提高问题求解的可行性。此外,含时间约束的优化问题可能存在多个解,致使序列迭代难以收敛,通过罚函数及信赖域系数的自适应调整避免该问题,提高算法的收敛性。

2.4.1 终端约束的处理

考虑到终端约束过于严格会导致没有可行解,适当放宽终端经纬度的限制,在终端位置约束不能满足的情况下接受最接近目标点的解。定义误差变量λe,φe,则每一次迭代求解结果中终端经纬度均满足：

|λ(ef)-λf|≤λe, |φ(ef)-φf|≤φe

(35)

进一步将λe,φe加入目标函数,使求解得到的轨迹终点与目标点经纬度偏差最小:

J=pλe+qλφ

(36)

式中:p、q为自适应系数,取值由2.4.3节给出。

2.4.2 目标函数中时间项的处理

针对问题P1,直接将线性化后的时间项加入到目标函数中,即

(37)

针对问题P2,在求解模型中加入期望总飞行时间约束：

(38)

式中：Tri、τi第i个离散点处的时间项系数；Tc为协同时间；ΔT为当前迭代过程中的时间误差,将ΔT加入到目标函数中,即

J=mΔT

(39)

式中:m为自适应调整的系数,其取值策略由2.4.3 节给出。当ΔT趋于0时,序列凸化求解得到的轨迹将满足协同时间的要求。

2.4.3 罚函数系数及信赖域自适应调整策略

在实际求解过程中,滑翔段最长、最短总时间及固定总时间等指标对应的轨迹形式并不唯一,存在多个解对应的目标函数值相同的情况,从而导致在序列迭代过程的末段,求解得到的结果在2条不同的轨迹形式间不断振荡,难以收敛。因此本文采用一种罚函数系数及信赖域自适应调整策略,即将飞行路径角相对于预设平滑剖面的偏离程度加入罚函数,而后不断降低其在罚函数中的权值系数,同时收缩信赖域,以保证求解过程能够收敛,并且得到的轨迹较为平滑。飞行路径角剖面搜索范围的变化趋势如图3所示。

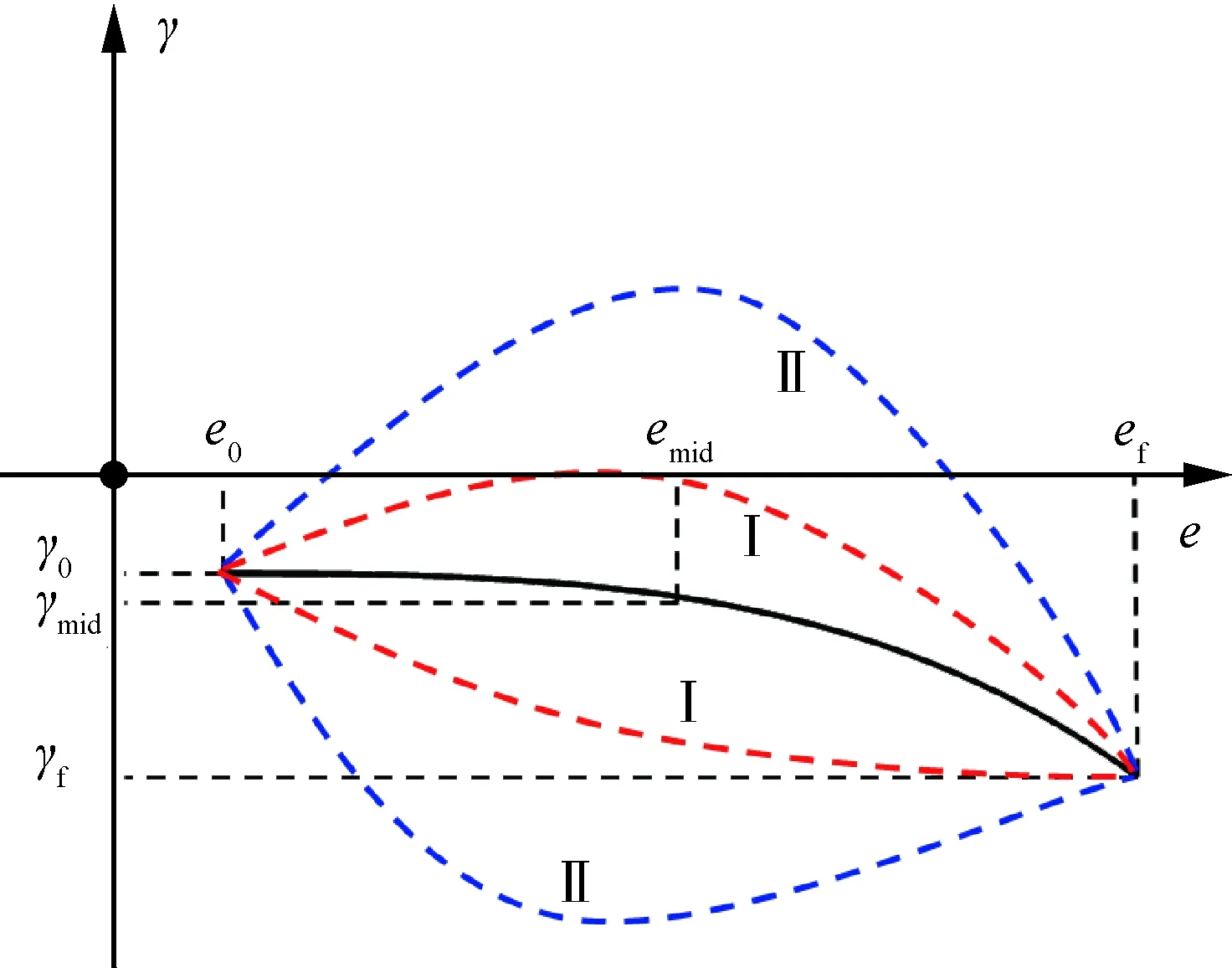
图3 飞行路径角剖面搜索范围变化示意图

引入式(22)对应的飞行路径角预设剖面作为求解过程中的软约束,即在第i个离散点处飞行路径角γi需满足：

|γi-γ0,i|≤Δγi,i=1,2,…,N

(40)

在序列迭代的开始阶段,取较大的n值,此时将在图2中的“Ⅰ”区域内搜索可行飞行路径角剖面,求解的主要指标为轨迹的平滑性。随着序列迭代的进行,逐步降低n值,飞行路径角预设剖面对轨迹求解的影响逐渐减弱,搜索区域将扩大至区域“Ⅱ”,有利于在平滑的初始轨迹附近搜索得到最优解。则问题P1、P2的目标函数可表示为

(41)

式中:p、q、m、n为自适应调整的系数,第k+1次迭代求解时各系数表达式为

(42)

由于动力学方程及各类约束的线性化过程基于小扰动假设,因此只有待求解变量在原参考点附近取值,即相邻两次求解结果满足式(43)所示的信赖域约束时,离散后的求解模型才是对原非线性问题的有效近似。若信赖域半径过小,则求解过程中搜索的范围有限,可能收敛不到最优解；若信赖域半径过大,虽然易于找到最优解,但对于存在多个最优解的情况,序列凸化算法难以收敛,因此采用一种信赖域自适应收缩策略,定义第次迭代求解时的信赖域约束为

|x(k+1)-x(k)|≤η(k)δ

(43)

式中:x=[r,λ,φ,γ,ψ]T;δ为各状态量的初始信赖域[δr,δλ,δφ,δγ,δψ]T;η(k)为随序列迭代次数改变的系数,其表达式为

(44)

式中:ω=1-|(J(k-1)-J(k-2))/J(k-2)|;ε为预先设定的阈值,0<ε<1/2;η(k)的选取由收敛系数ξ及ω共同决定。系数ω反映了代价函数值J的变化,当ω小于阈值ε时,认为代价函数J的值下降不明显,解已经趋于最优解附近,为加快收敛速度,避免因存在多个最优解导致求解结果在多条轨迹间振荡的情况,引入收敛系数ξ,满足0<ξ<1。ξ值过大或过小会导致轨迹精度较差或收敛较慢,因此本文取ξ=0.5；当ω大于阈值ε时,令ξ=1。

在迭代初始阶段,信赖域半径δ可选取为一个足够大的数值,以保证能够在较大的初始解空间范围内搜索得到近似最优解。在后续迭代过程中,随着信赖域半径的减小,最优解的搜索空间逐渐减小,易于序列凸化算法的收敛,相比于固定信赖域半径方法的求解结果更接近全局最优解。

2.5 序列迭代求解过程

在对问题凸化和离散化之后,多高超声速飞行器滑翔段时间协同弹道规划问题可被分为P1、P2两个序列二阶锥规划问题,两个子问题的求解模型可表示为

(45)

2) 固定总时间约束下的轨迹规划问题

(46)

本文所采用的序列二阶锥规划算法流程如图4所示,具体的求解步骤如下。

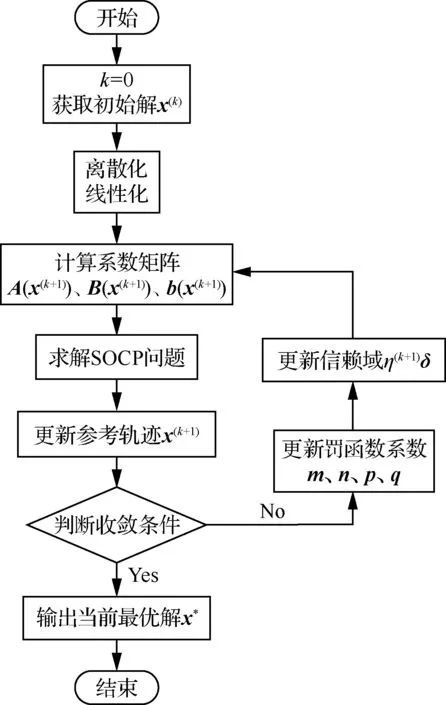
图4 序列凸化算法流程图

步骤1令迭代次数k=0,迭代求取飞行路径角初值剖面,获取轨迹的初始解x(0),并将x(0)定义为参考轨迹x(k)。

步骤2对动力学方程及各类约束进行凸化、离散化,将参考轨迹代入计算动力学约束中的系数矩阵A(x(k))、B(x(k))、b(x(1))等,得到SOCP形式的问题求解模型。

步骤3利用SOCP算法得到最优解x(k+1),更新参考轨迹。

步骤4判断|x(k+1)-x(k)|<ε是否满足,其中ε为预先设定的常值向量,若收敛条件不满足,则更新罚函数系数m、n、p、q及信赖域半径η(k-1)δ,转步骤2,若收敛条件满足,则转步骤5。

步骤5得到优化问题的最优解为x(k+1),序列迭代结束。

3 仿真结果与分析

为验证所提滑翔段时间协同轨迹规划算法的有效性,以3个滑翔飞行器构成的集群为例,基于2种协同任务场景进行了数值仿真实验。首先,针对问题P1,分别运用改进序列凸化算法与基于非线性规划求解器GPOPS的h-p自适应Radau伪谱法,求解了最长、最短再入时间对应的轨迹。而后在确定协同时间的基础上求解了问题P2,分析了含时间约束的优化问题求解过程中,本文算法与传统序列凸化算法的收敛效果。最后对比了序列凸化算法与伪谱法的轨迹规划结果。

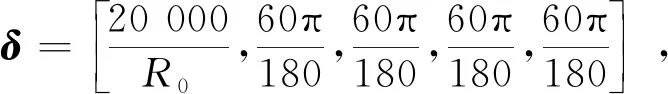
3.1 多飞行器不同起始点协同再入

表1给出了各飞行器及目标点的初始状态信息,表2给出了不同算法对于飞行极值时间的求解结果。

表1 各飞行器及目标点初始状态

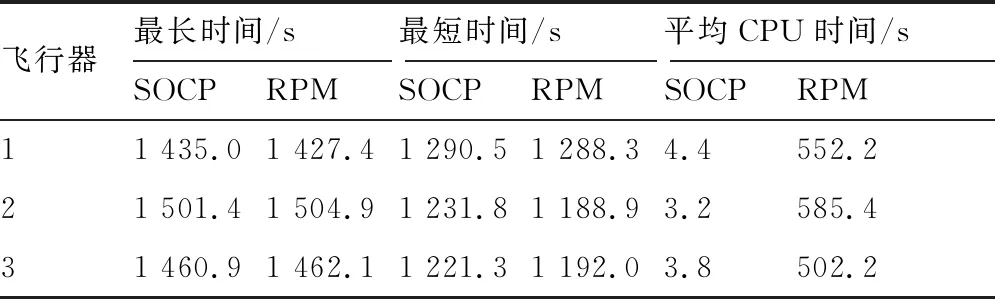
表2 序列凸化(SOCP)与伪谱法(RPM)结果对比

由表2可知,各飞行器的再入总时间可调范围分别为144.5 s,269.6 s,239.6 s。由各飞行器与目标点的相对位置可以看出,初始航向角对飞行器的再入总时间极值有着较大影响,飞行器2、3相比于飞行器1的可调范围显著增大,当初始速度方向指向目标时,飞行器的再入总时间将有更大的可调范围。SOCP算法得到的总时间可调范围与伪谱法基本一致,伪谱法求得的最短时间稍小于SOCP算法,总时间可调范围稍大,但SOCP算法的计算时间要明显优于伪谱法。根据时间协同策略可确定3个飞行器的协同再入总时间为1 430 s,利用本文提出的固定期望总时间约束下的轨迹规划方法求解再入协同轨迹,飞行器1～3的三维协同轨迹与其各自的最速下降轨迹地面投影对比如图5和图6 所示。表3 给出了各飞行器轨迹数值积分验证结果的终端状态精度情况。

图5 协同轨迹三维图

图6 协同轨迹地面投影

表3 协同轨迹积分验证结果

由图5 可知,各飞行器在到达时间相同的基础上,能够实现终端飞行路径角及航向角的一致。图6 中各飞行器为实现最短时间再入,速度方向基本保持在起始点与目标点连线的纵向平面内,轨迹的地面投影均较为平直。为实现再入时间的一致,各飞行器在初始阶段偏离了最速下降方向,通过侧向机动的方式延缓到达时间,从而实现时间协同。根据表3中的积分验证结果,终端最大高度误差为140 m,最大再入总时间误差为6.28 s,终端飞行路径角与航向角误差均小于1°,满足精度要求。

3.2 多飞行器同起点序列式再入

假定3个滑翔飞行器从同起点再入,在滑翔段起始点分离,要求序列到达同一目标点,验证了算法的有效性。表4 给出了仿真初始条件,图7～图9给出了各飞行器轨迹对比及热流、动压、过载约束满足情况,图10以问题P1的求解过程为例,展示了本文方法对于序列凸化算法收敛性的改进情况。

图7 序列到达轨迹高度-能量剖面对比

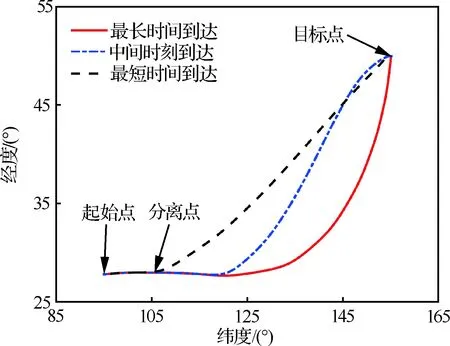
图8 序列到达轨迹地面投影对比

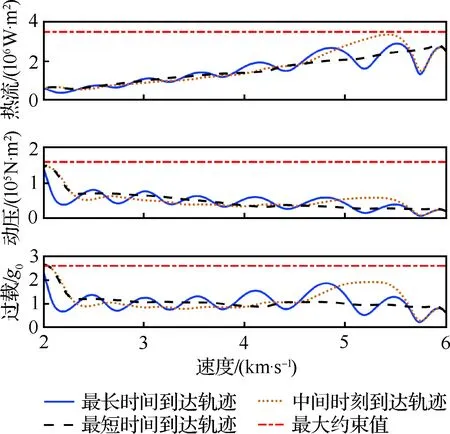
图9 滑翔段动压、过载、热流变化情况

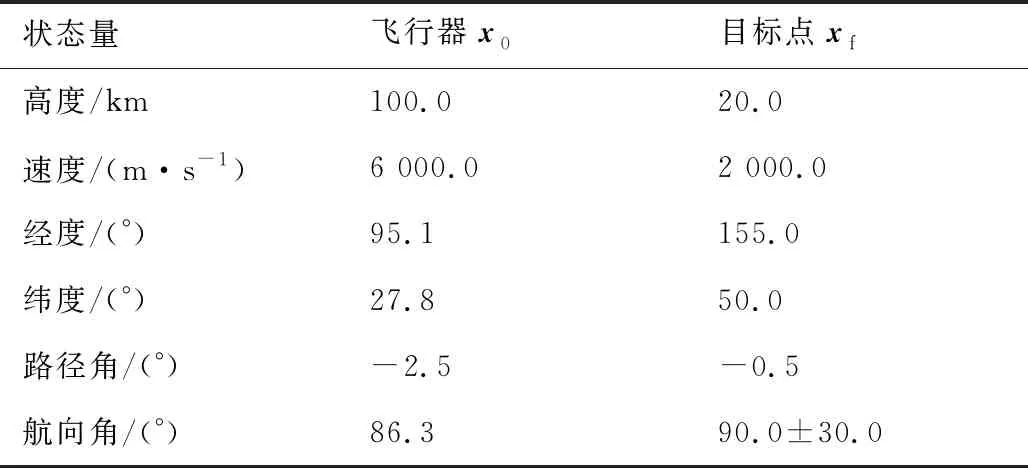
表4 仿真初始条件

图7和图8表明最长时间到达轨迹呈周期性

进一步将本文变系数方法与传统序列凸化方法、固定罚函数及信赖域收缩系数方法的迭代求解过程进行对比。图10给出了本文方法对于求解最短时间再入问题收敛过程的影响情况。图中,纵轴为各方法在第次迭代过程中求解得到的滑翔段总时间相对于最优解的绝对误差。可以看出,本文变系数方法最先收敛至最优解；传统序列凸化方法求解结果不断振荡,说明存在多组解对应的目标函数值相同,使得算法难以收敛；罚函数

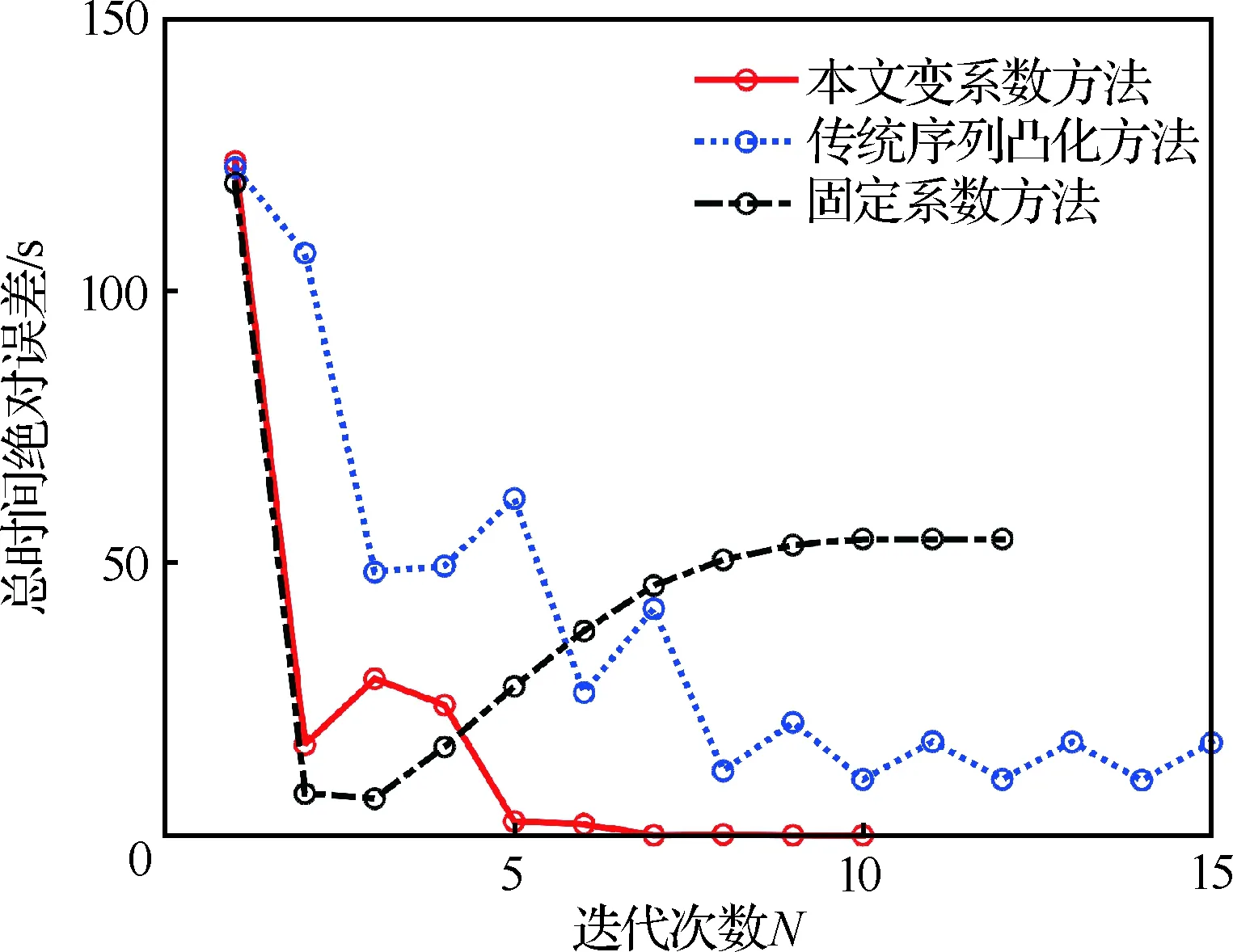
图10 不同方法最短再入时间求解结果的绝对误差随迭代次数变化情况

及信赖域系数均固定的方法在开始阶段目标函数值收敛趋势与变系数方法一致,但在第3次迭代后偏离最优解,说明目标函数中的时间项受到了其他指标影响,未在序列优化后期起主要作用。

由表5可得,本文方法与伪谱法优化得到的到达时间基本一致,终端状态量精度均满足要求。传统序列凸化方法未收敛至最优解,导致终端存在500 m高度偏差,最短再入总时间同样出现较大误差。接下来验证了本文方法在处理给定期望总时间约束下的轨迹求解的有效性,并与伪谱法、MPSP方法进行对比。

表5 不同方法终端精度对比

选取1 500 s作为期望总时间,分别进行给定总时间约束条件下的轨迹解算,图11和图12给出了3种方法的纵向剖面及地面轨迹投影的结果对比。其中,序列凸化方法总用时4.24 s,MPSP方法用时10.82 s,伪谱法用时105.02 s。3种方法求解结果都能够满足期望总时间约束,终端精度均处于合理范围。由规划结果可知,同一滑翔段总时间对应的轨迹形式并不唯一,三者优化得到的地面轨迹基本一致,但序列凸化方法计算得到的纵向轨迹相比于伪谱法及MPSP方法上下跳跃幅度明显减小,轨迹更为平滑,且解算用时更短。此外,相比于序列凸化及伪谱法,MPSP方法的收敛性对于控制量初值选取较为敏感。

图11 高度-能量剖面对比

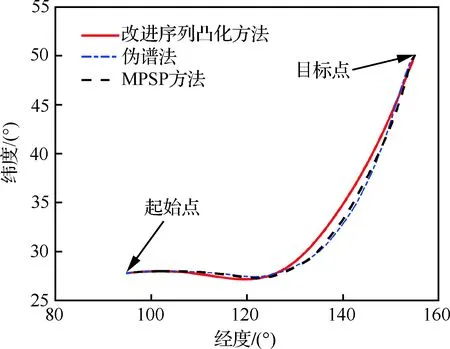
图12 地面投影轨迹对比

3.3 算法适应性测试

进一步,分别在初始点状态大范围变化及小范围摄动2种情况下,对算法的收敛性及快速性进行仿真测试。首先,选取期望再入总时间为1 400 s,目标终端状态为

xf=[hf,vf,λf,φf]=[20 km,2 km/s,155°,50°]

选取多个不同的起始点状态,以验证算法的收敛性和快速性。各次仿真的初始状态及算法各次求解用时情况如表6所示。图13和图14给出了各次求解得到的轨迹积分验证结果。

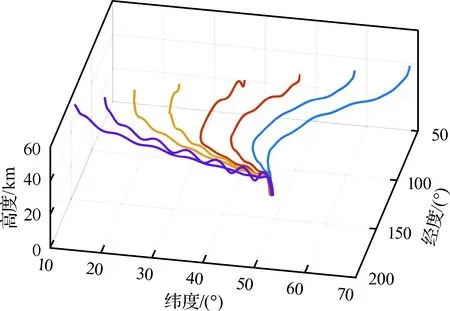
图13 三维轨迹

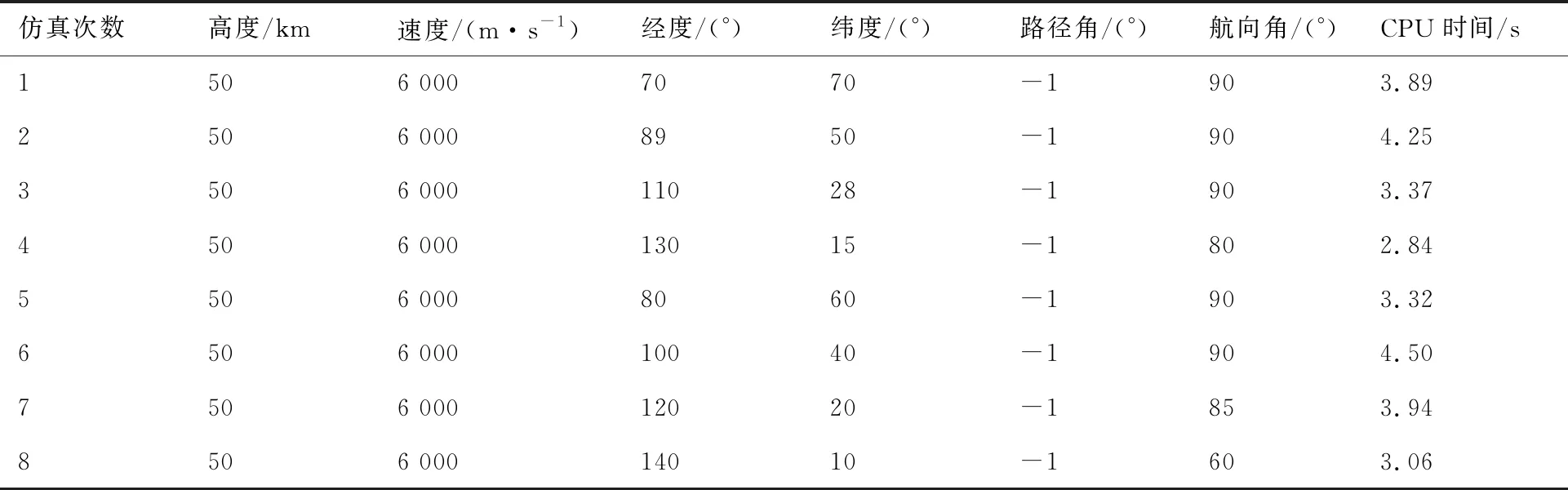
表6 仿真初始条件

各次仿真优化求解的平均时间为3.64 s,最大总时间偏差为7 s ,最大终端高度偏差为516 m,最大终端速度偏差为62 m/s,最大终端经度偏差为0.63°,最大终端纬度偏差为0.46°。

最后,通过蒙特卡洛方法测试所提固定总时间约束下轨迹规划算法对于初始经纬度变化的适应性。目标终端状态为

xf=[20 km,2 km/s,155°,

50°,-0.5°±1°,90°±1°]

初始点状态的取值上限定义为

x0max=[50 100 m,6 050 m/s,90°,45°,0°,90°]

初始点状态的取值下限定义为

x0min=[49 900 m,5 980 m/s,88°,50°,-1°,90°]

在上述初始点范围内随机取值并利用序列凸化算法求解满足再入总时间约束的可行轨迹。共进行50次仿真,各次求解得到的轨迹通过数值积分验证后的结果如图15～图17所示。

图15 蒙特卡洛仿真结果

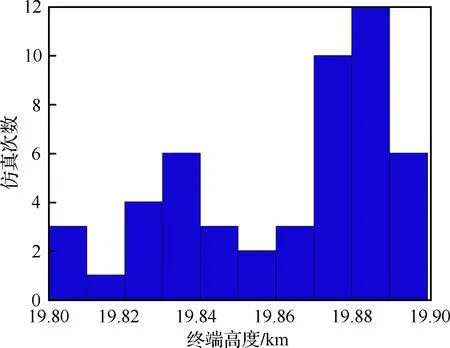
图16 终端高度分布

图17 再入总时间分布

由仿真结果统计可得,序列凸化算法各次仿真平均CPU用时为3.92 s；终端高度平均偏差为136.05 m,最大偏差为214.59 m；再入总时间平均偏差为2.37 s,最大时间偏差为8.04 s；平均经纬度偏差为0.12°,终端航向角及飞行路径角均满足误差要求。

4 结 论

1) 针对多高超声速滑翔飞行器集群协同再入问题,设计了“探测-打击-评估”一体化模式下,集群内部时间协同的轨迹规划方案。

2) 给出了集群协同时间的确定策略,解决了给定期望再入协同时间约束下的多飞行器轨迹快速规划问题。

3) 提出了一种罚函数与信赖域自适应调整策略,能够避免存在多个最优解情况下的轨迹振荡问题,提高了序列凸化算法的收敛性。

4) 仿真结果表明,所提改进序列凸化算法能够适应不同的时间协同再入任务,收敛性受初值影响相对MPSP算法较小,求解结果相比于伪谱法轨迹更加平滑,计算速度优于伪谱法。