考虑进气约束的高超声速飞行器预定性能控制
丁一波,岳晓奎,代洪华,崔乃刚
1. 西北工业大学 航天学院,西安 710072
2. 哈尔滨工业大学 航天学院,哈尔滨 150001
吸气式高超声速飞行器因其高速度、大射程、快响应的特点,具有重大的军事价值与潜在的经济价值[1-2]。但是,相比传统飞行器,吸气式高超声速飞行器具有强非线性、静不稳定的特性;由于其腹部超燃冲压发动机的影响,飞行器的推进系统和气动系统之间会产生强耦合;又由于其工作环境气动现象复杂、机身气动参数难以准确获取,飞行器易遭遇外界扰动和参数摄动影响[3-4]。不仅如此,吸气式高超声速飞行器跟踪控制的瞬态性能对飞行状态有着重要的影响,较大的超调量会生成过大的飞行攻角,无法维持吸气式发动机的进气条件,引起发动机熄火[5-6]。上述诸多问题均导致吸气式高超声速飞行器的控制问题复杂而极具挑战性,因此需要针对吸气式高超声速飞行器研究同步考虑跟踪误差性能与发动机进气条件约束的控制方法。
数十年以来,国内外学者针对吸气式高超声速飞行器的建模工作开展了大量研究。目前研究中常采用的吸气式高超声速飞行器动力学模型主要针对2种构型:锥体加速器构型(Winged-cone)和乘波体构型(X-43A)。锥体加速器的前体是一个轴对称圆锥体,具有大长细比和大后掠角,升阻比较大,而发动机模块环绕整个机体[7]。美国国家航空航天局(NASA)的Shaughnessy等对Winged-cone构型高超声速飞行器的几何外形特点和发动机结构进行了详细描述,并以图表形式给出了各个气动力和气动力矩系数与攻角、马赫数的关系,为Winged-cone等构型飞行器的后期研究提供了基础[8]。Mirmirani等根据NASA公布的Winged-cone构型高超声速飞行器的数据,用多项式拟合出六自由度的高超声速飞行器的数学模型,并给出较为详细的气动力以及力矩表达式[9]。后来Mirmirani用计算流体动力学得到的数据填补风洞试验数据的空缺,通过曲线拟合方法,给出了与攻角、马赫数、侧滑角以及舵偏量相关的气动力和气动力矩表达式,建立了Winged-cone构型飞行器的气动数据库,并通过仿真计算,验证了气动模型的准确性。对于乘波体构型的高超声速飞行器的运动学以及气动力建模的研究,国外的成果有:Schmidt和Chavez用第一性原理建立了三自由度的高超声速飞行器模型[10]。其中气体流动假设为准一维和准稳定的,空气动力和力矩由牛顿碰撞理论得到,超燃发动机则建模为简单的静态模型。美国空军实验室的Bolender以X-43A构型为例,采用斜激波和Prandl-Meyer理论代替牛顿碰撞理论[11],计算出高超声速飞行器表面的气动力以及弹性结构带来的斜激波振荡对气动力的影响,建立了包含推力、气动力和弹性结构间相互耦合的高超声速飞行器“真实模型”[12-13]。Mirmirani等运用压缩流理论分析正面激波的倾斜角、压力以及在发动机入口处马赫数,并把气动力和推力的耦合进行量化,提出了X-43A带有气推耦合的纵向模型,此模型是加州州立洛杉矶分校利用缩小尺寸的X-43A建模的[14]。Morelli等利用飞行试验数据对气动参数进行评估[15],Engelund详细讲述了飞行试验任务以及各阶段的气动数据,研究了高超声速飞行器气动与推进系统的相关特性[16]。由于Bolender的“真实模型”过于复杂,为了便于实际使用,Parker等采用最小二乘曲线拟合方法,求解气动力与力矩的多项式拟合表达式,获得曲线拟合模型(Curve-fitted model)。但是由于Parker等结合了反馈线性化和增广LQR控制的方案,而曲线拟合模型却无法直接实现反馈线性化,所以Parker等将曲线拟合模型中的高度动力学与弹性状态移除,将升降舵对升力的耦合影响置为零,并且为燃油当量比增加二阶动力学扩展,进一步简化获得了面向控制的模型(Control-oriented model)[17]。Sigthorsson和Serrani采用曲线拟合的方法简化“真实模型”,并将简化出来的模型推导成线性参变形式,以便于使用线性控制方法设计控制器[18]。Oppenheimer等考虑到非定常气动力的存在,用活塞理论求解飞行器气动表面的压力分布,建立纵向气动模型,后期又将活塞理论用于考虑飞行器弹性结构形变,获得了弹性气动模型[19-20]。随着理论不断健全,黏性效应、气动热都被考虑到模型中[21-23]。在本文中,并未采用线性控制方法,也未采用反馈线性化方案,所以为了实现更为精确的控制,本文的高超声速飞行器模型并不采用线性参变形式或面向控制的模型,而是采用了高度非线性的曲线拟合模型。
迄今为止,已有许多先进控制理论应用于吸气式高超声速飞行器的控制系统设计中,如:LQR控制、鲁棒H∞控制、模糊控制、神经网络控制、反步控制、滑模控制等。Ur Rehman等针对高超声速飞行器提出了一个极小极大LQR控制器[24],Parker等应用带有积分增广的LQR控制器补偿面向控制的模型中的不确定度[17]。为了减小神经网络的计算压力,Bu等在文献[25-26]中结合了新型改进反步控制器、神经网络近似与Minimal-learning-parameter技术。Zhang等基于文献[27]的算法应用准连续高阶滑模控制器使高超声速飞行器在有限时间内跟踪期望指令[28]。
吸气式高超声速飞行器采用机体发动机一体化设计技术,发动机安装于机身下部,由进气道、燃烧室和尾喷管组成,进气口处设计有可移动的罩门,以保证发动机在非设计工况下获取最大空气质量流。这种机身发动机一体化的设计能够为飞行器提供强大推力、提高升阻比以及减少燃料负载。但也会产生不利因素,即推进系统将与操纵面相互干扰,导致空气动力学与推进系统之间存在强耦合,为飞行器控制系统的设计提出了更高的要求和挑战。由于气推耦合的影响,在实际飞行控制过程中,吸气式高超声速飞行器的瞬态性能与稳态性能同样需要受到关注。若系统跟踪误差瞬时超调较大,会产生过大攻角,无法维持吸气式发动机的进气量,导致发动机熄火[29-30]。传统飞行控制方法难以满足吸气式高超声速飞行器的性能约束要求,因此需要针对飞行器的瞬态性能设计预定性能控制。预定性能控制指的是系统跟踪误差满足期望超调量、收敛速率与稳态误差。通过限定飞行状态跟踪误差(速度、高度、攻角变化范围)的变化趋势,能够有效满足飞行性能约束与攻角幅值约束,保证吸气式发动机正常工作所需的进气量。Wang等设计了新型自适应漏斗控制以改进传统方案,并与滑模控制结合提升系统瞬态性能[31]。在文献[32]中,Dong等在自适应有限时间控制中加入障碍李雅普诺夫函数限定高超声速飞行器的状态量跟踪误差。坐标转换法是由Bechlioulis与Rovithakis[33]提出的方案,该方法首先设计预定性能边界函数,然后对系统状态跟踪误差进行坐标转化得到新的无约束坐标。通过设计控制律保证新坐标有界即可将原本的跟踪误差限定在性能边界函数内。作为坐标转换法中的重要一环,预定性能函数直接决定了跟踪误差的性能,因此学者们多着眼于性能函数的设计与改进。在文献[34]中,Bu采用传统的指数收敛形式性能函数,并应用反双曲正切函数进行坐标转换。文献[35]与文献[36]分别基于双曲余切与双曲余割函数设计预定性能边界函数,相比传统方法,该方案无需精确已知系统跟踪误差的初值。
综合上述分析可知,现有的性能函数能够自由调节函数收敛速率,但是实现较快收敛速率需要付出的代价是较大的初始控制量,这在实际控制幅值受限的吸气式高超声速飞行器中通常难以实现。因此,需要研究能够灵活调整收敛速率且初始控制量较小的新型性能函数[37]。而且,如何基于性能函数方法针对吸气式高超声速飞行器设计同步考虑跟踪误差性能约束与发动机进气条件约束的控制器是一个需要解决的难题。因此,本文基于新型设定时间性能函数提出了一种约束预定性能控制器,能够满足飞行器跟踪误差的性能约束与吸气式发动机的进气约束。设计的新型设定时间性能函数能够保证性能函数变量在预设时刻精确收敛至稳态值。
1 高超声速飞行器动力学建模
本节首先给出高超声速飞行器的动力学方程,然后将其拆分为速度和高度2个子系统,最后给出跟踪误差的预定性能条件与进气约束。
1.1 高超声速飞行器数学模型
高超声速飞行器的纵向动力学模型为
(1)
式中:V、h、γ、α、Q分别为速度、高度、飞行路径角、攻角和俯仰角速度;m、g、Iyy分别为质量、重力加速度与转动惯量;T、M、L和D分别为推力、俯仰力矩、升力和阻力。推力与气动力、气动力矩经由曲线拟合近似可得:
(2)

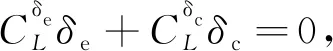
考虑到高超声速飞行器的任务需求与实际物理约束,在飞行过程中,系统状态需要保持在如表1 所示特定允许范围内[17, 38]。

表1 状态量与控制量允许范围
1.2 子系统分解
基于功能分解,飞行器动力学系统(式(1))可拆分为2个子系统:速度与高度子系统。速度阶跃指令信号Vc与高度阶跃指令信号hc通过2个预滤波器可以获取2个子系统的期望信号Vd与hd[39]:
(3)
(4)
式中:ωd1和ζd1为角频率和阻尼比,其取值分别为ωd1=0.03 rad/s,ζd1=0.95。2个预滤波器的功能是将阶跃的指令信号Vc与hc调制为光滑且可导的期望信号Vd与hd。
定义速度、高度、飞行路径角跟踪误差分别为eV=V-Vd、eh=h-hd与eγ=γ-γd:
(5)
(6)
式中:dVT、dγT、dQT分别表示气动参数摄动及外部扰动作用于速度、飞行路径角、俯仰角速度动力学上的扰动;其余符号定义如下:
(7)
(8)
假定气动系数与结构系数都受到参数摄动的影响。定义Pr为实际结构参数,包括质量m、转动惯量Iyy、参考面积S;P0为其标称值。符号Cr表示实际气动拟合参数与推力拟合参数,C0为其标称值。在实际控制器设计中,仅有标称参数P0与C0可以获得,因此利用标称值P0与C0替换式(7)与式(8)中的实际值Pr和Cr可以计算得到标称函数FV0、GV0、Fγ0、Gγ0、Fα0、Gα0、FQ0、GQ0。式(5)和式(6)的误差动力学可以表示为
(9)
(10)
式中:ΔV、Δγ、Δα与ΔQ表示由外部扰动或参数摄动影响引发的集总扰动。
1.3 问题陈述
由于1.1节中所述气推耦合的影响,吸气式高超声速飞行器的飞行状态会直接影响发动机工作情况,主要体现在飞行攻角的大小会改变发动机进气量,若攻角幅值超出允许范围,发动机将出现进气不足现象,产生热滞,导致推进系统瘫痪。因此需要同时关注飞行器实时控制下的飞行状态瞬态与稳态性能,以限制攻角幅值变化范围,保证发动机正常工作[40]。可保证发动机进气约束的攻角幅值范围满足如下条件[41-42]:
|α|≤Aα=aαV+bαV∈[Vmin,Vmax]
(11)
式中:Vmin≈4Mam/s;aα与bα为常数。当V=Vmin时,aαVmin+bα=0。由式(11)可知,当飞行速度低于4Ma时,吸气式超燃冲压发动机无法工作;当飞行速度大于4Ma时,发动机正常工作允许的最大攻角值Aα随速度的增大而增大[43]。
根据上述条件可知,吸气式发动机的进气约束与飞行速度、飞行状态等都密切相关。因此需要对速度、高度、攻角等状态的跟踪误差进行瞬态性能和稳态性能2方面的精确控制和限制。定义速度与高度跟踪误差的预定性能条件为
-δVLρfV(t)
(12)
-δhLρfh(t)
(13)
式中:ρfV(t)与ρfh(t)分别为速度与高度跟踪误差的预定性能函数,其界定了期望瞬态性能(最小收敛速率,最大超调)与稳态性能(稳态误差)[44];δVL、δVU、δhL、δhU为界限参数,其满足:
δVL,δVU,δhL,δhU∈(0, 1]
(14)
本文的控制目的是设计考虑约束的非线性控制器,使得高超声速飞行器的速度与高度跟踪误差满足期望预定性能式(12)与式(13),即保证飞行器跟踪误差的瞬态性能与稳态性能满足预期需求。同时,飞行攻角实时满足条件式(11),保证超燃冲压发动机正常工作。
2 约束预定性能控制器设计
本节控制器设计的结构安排如下:首先针对速度子系统提出有限时间预定性能控制器,对受约束的速度跟踪误差进行无约束转化,并结合新型设定时间性能函数与一致收敛观测器,实现转换误差的快速有限时间收敛,保证速度跟踪误差满足预定性能约束式(12);然后基于新型固定时间滤波器,为高度子系统提出指令滤波反步预定性能控制器,该控制器针对高度跟踪误差设计了预定性能控制;另外,在反步控制中,限定攻角的虚拟控制信号幅值不超过Aαc,并对攻角跟踪误差执行预定性能控制,令其性能函数最大值max{ρfα(t)}与Aαc之和不大于进气条件约束下的最大攻角值Aα,则可保证飞行器满足攻角幅值约束式(11)。约束预定性能控制器的完整结构框图如图1所示。

图1 约束预定性能控制器结构
2.1 速度子系统有限时间预定性能控制器
本节首先设计新型设定时间性能函数,然后基于无约束转化设计有限时间控制律。
2.1.1 设定时间性能函数设计
为了保证系统跟踪误差的瞬态响应和稳态值满足期望预定性能,首先需要构建函数值大于零的光滑预定性能函数作为预定性能边界[45]。本文提出如下多项式形式的新型设定时间性能函数:
ρfV(t)=aV3t4+aV2t3+aV1t2+cVρrt+cVρ0
(15)
式中:aV3、aV2与aV1的表达式为
(16)
其中:cVρ0、cVρr、ρfV∞与TfV为调节参数。cVρ0为正数,表示初始误差界限;cVρr表示性能函数初始变化方向;ρfV∞为函数ρfV(t)的稳态收敛值;TfV为ρfV(t)收敛至稳态值ρfV∞的设定时间。
为了保证跟踪误差eV初始处于预定性能区域式(12)内,性能函数参数需要满足[46]:
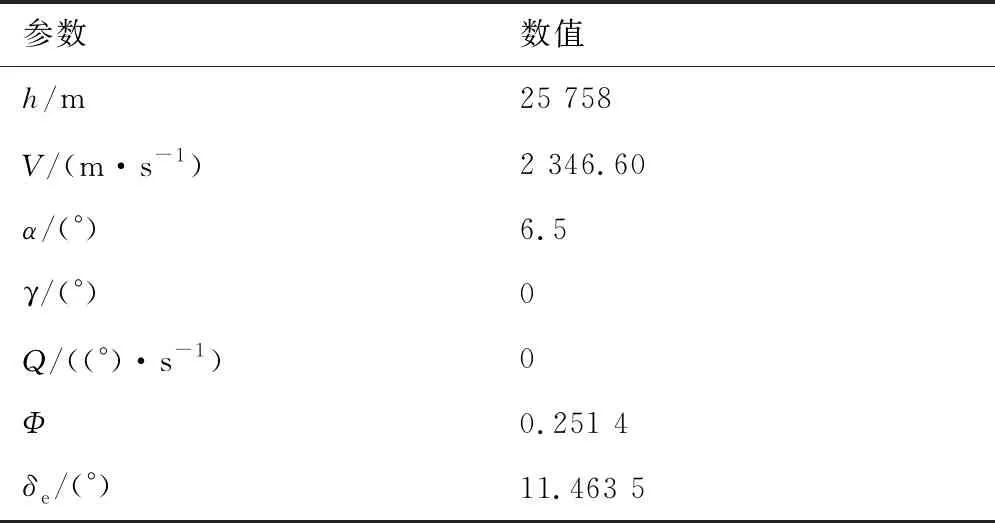
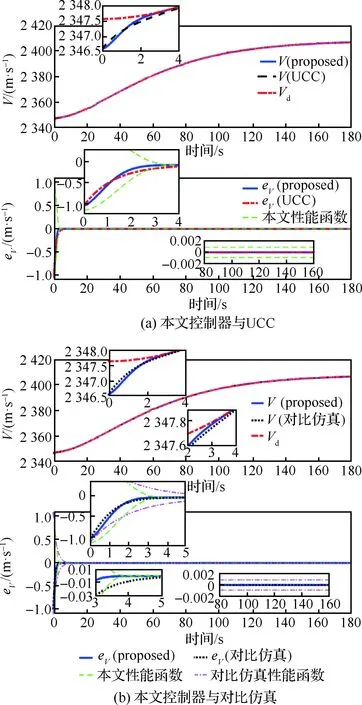
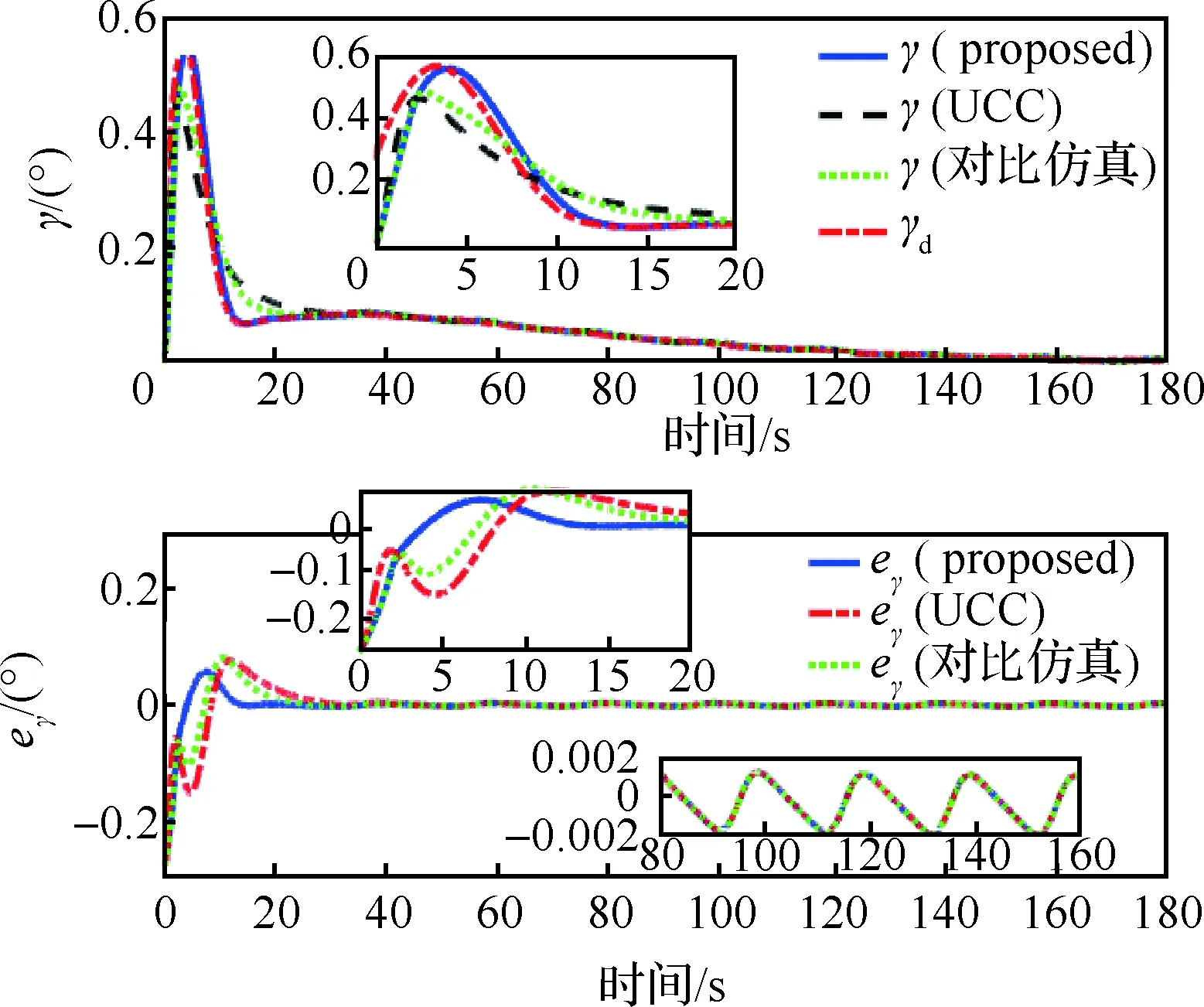
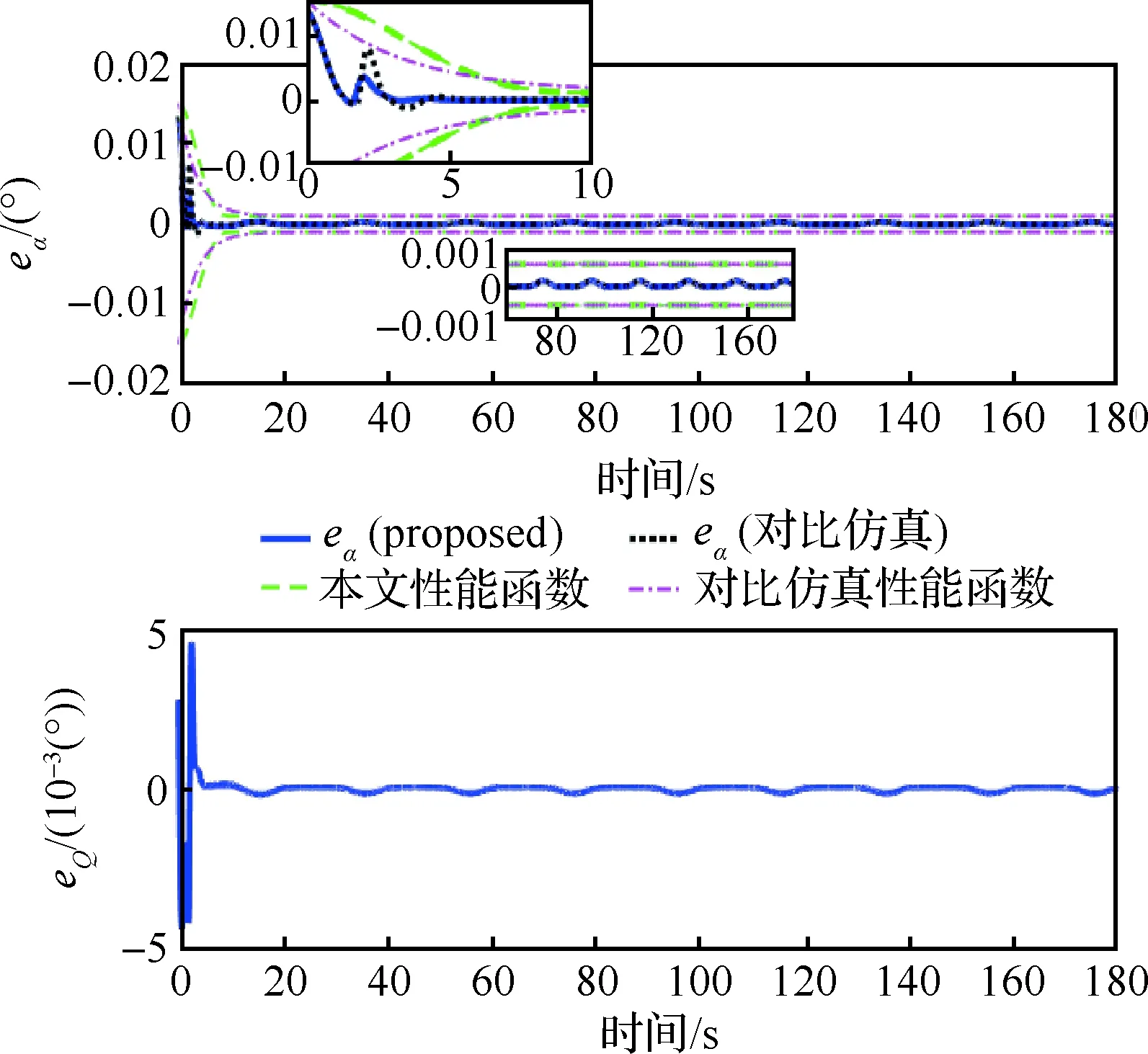
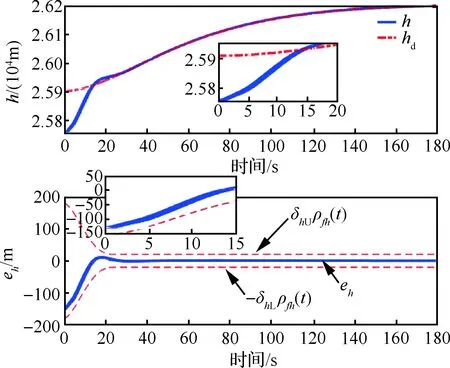
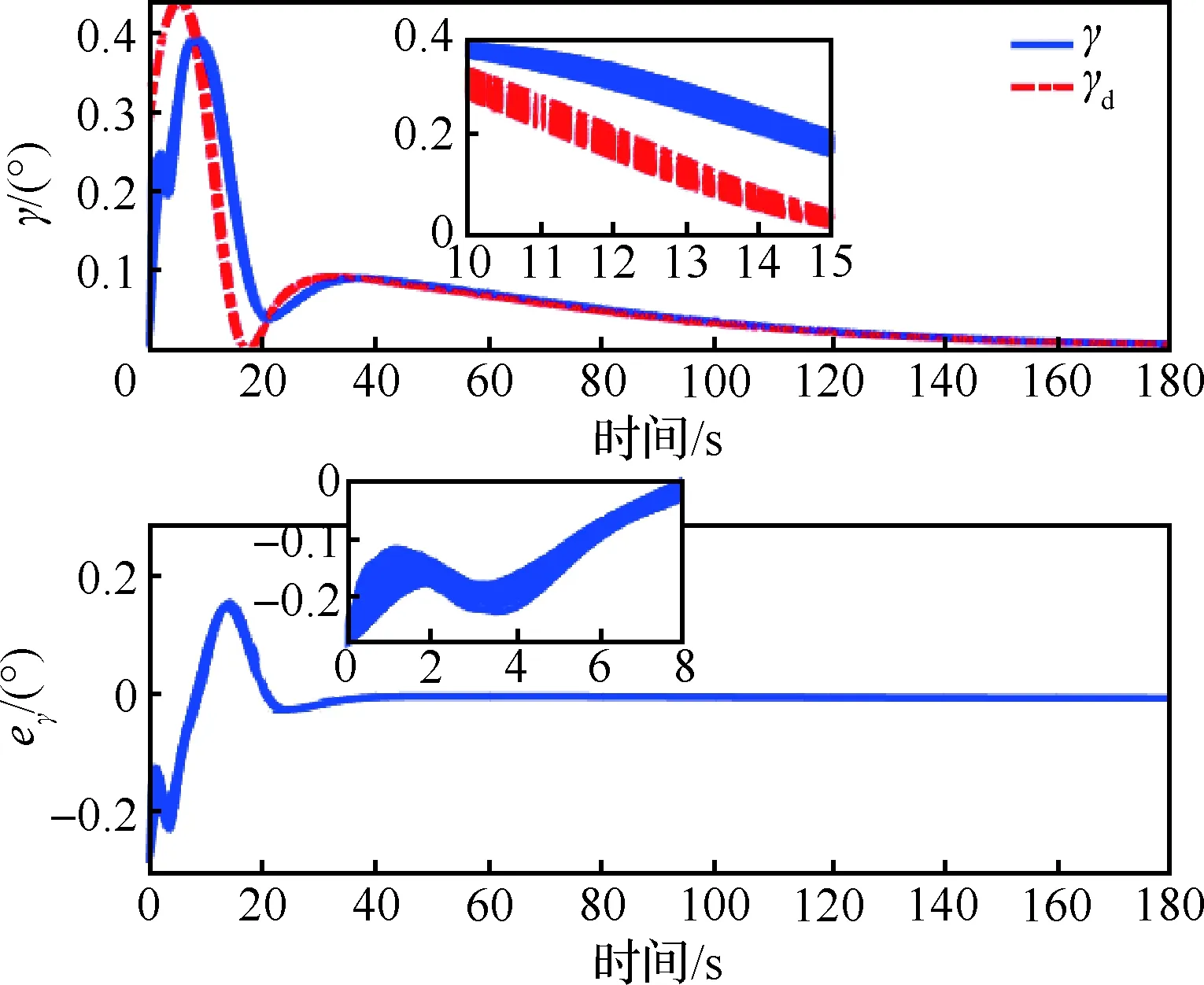
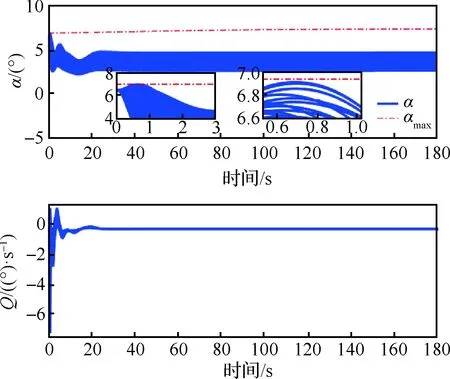
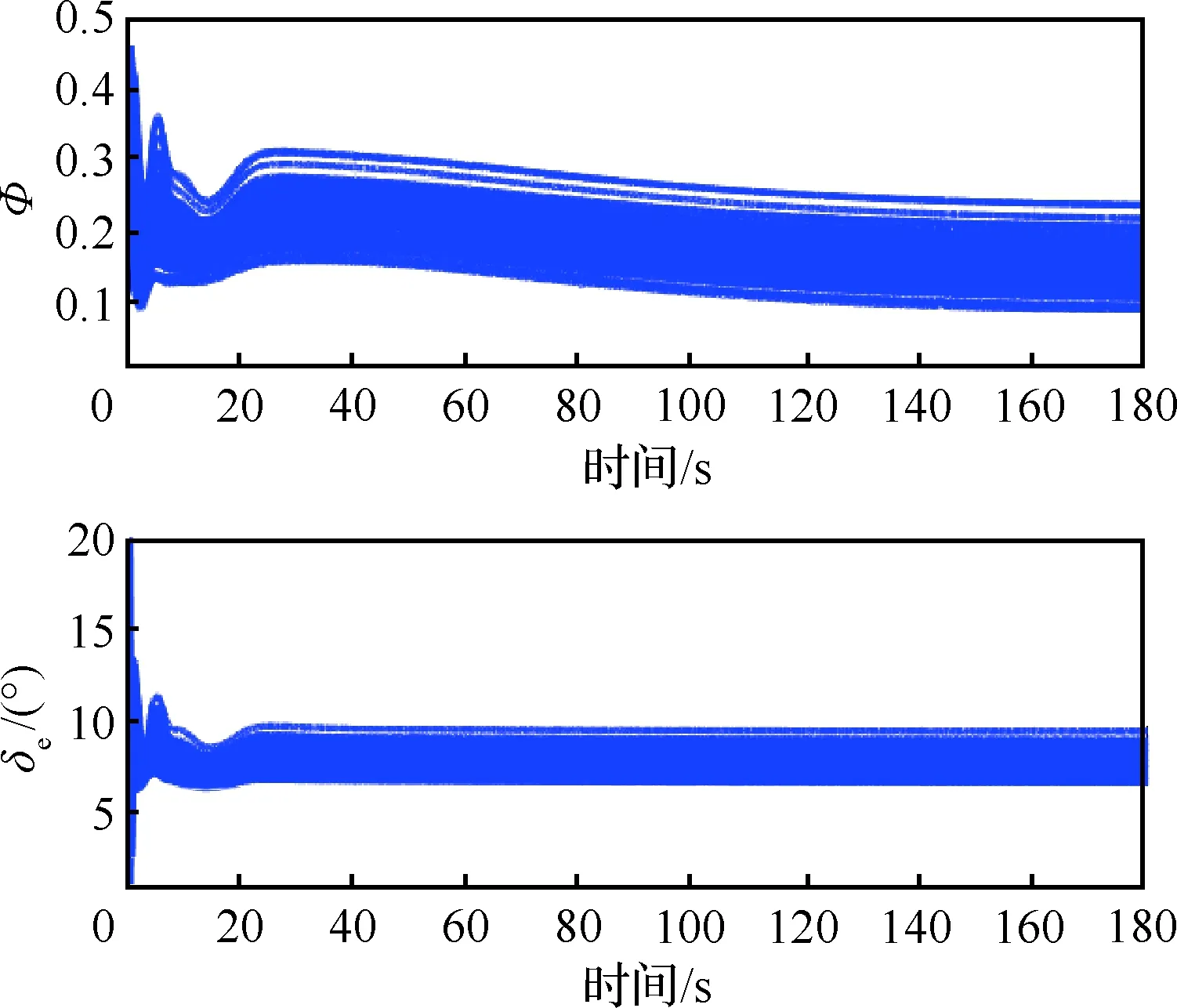
-δVLcVρ0 (17) 式中:eV(0)为eV的初始值。则式(17)等价于:当eV(0)≥0时,需要满足:cVρ0>eV(0)/δVU;当eV(0)<0时,需要满足:cVρ0>-eV(0)/δVL。综合2种情况,cVρ0参数选择应满足: (18) 注意式(18)中的符号函数sgn[eV(0)]只是用于获得初始速度跟踪误差eV(0)的正负性,根据其正负性计算cVρ0的选取范围。这里的符号函数并不会用于控制器设计中,所以并不会影响控制器的实际应用。令t=TfV可得: (19) 可见,性能函数式(15)能够在设定时间TfV处精确等于期望稳态收敛值,且ρfV(t)与其导数在设定时间处均连续光滑。 注释1考虑如下3种传统预定性能控制的性能函数[35,46-47]: (20) 式中:kρ为正设计参数,表示性能函数衰减速率。这3种性能函数都能够有效衰减直至期望稳态值,但是它们只能实现指数收敛。相比之下,设定时间性能函数能够保证ρfV(t)在预设时刻TfV精确等于稳态值,从而实现更快的收敛速度与更高的收敛精度。同时,设定时间性能函数中的参数cVρr可以调节函数初始变化方向,灵活调整衰减形式。 2.1.2 控制器设计 为了补偿速度子系统中扰动的影响,应用文献[48]中的一致收敛观测器精确估计扰动ΔV: (21) κA1=3,κA2=4.16,κA3=3.06,κA4=1.1 (22) 参数αA为充分小正常数;kAi需要保证多项式s4+kA1s3+kA2s2+kA3s+kA4满足霍尔维茨条件;参数θA定义为 (23) 下面设计速度子系统预定性能控制器。首先将受约束的eV转化为等价的无约束形式: eV=λVρfV(t)=S(εV)ρfV(t) (24) 式中:εV为转换误差;λV=S(εV)表示关于εV的光滑递增转换函数,其满足如下条件[46]: (25) 根据条件式(25)设计可用转换函数[49]: (26) (27) 结合式(21)的输出信号可得速度控制器: (28) 式中:kV,kVF>0, 0 (29) 定理1在控制律式(28)作用下,速度子系统转换误差εV能够在有限时间内快速收敛至0。因此速度跟踪误差eV可始终处于预定性能区域式(12) 内。 (30) 将式(28)代入式(30)可得: (31) (32) 其中: (33) 若参数kV设计满足:kV>1/2,则VV可在有限时间内收敛进入下述区域: (34) 收敛时间满足: (35) 其中:VV0为VV的初始值。 (36) 故在观测器收敛之后,εV将在有限时间内精确收敛至0。收敛时间满足: (37) 则εV有界,由式(25)得λV=S(εV)∈(-δVL,δVU), -δVL 本节设计指令滤波反步预定性能控制器,在保证高度跟踪误差期望预定性能的同时,满足攻角幅值约束。 首先针对高度跟踪误差设计性能函数: ρfh(t)=ah3t4+ah2t3+ah1t2+chρrt+chρ0 (38) 式中:ah3、ah2与ah1的表达式为 (39) 其中:chρ0、chρr、ρfh∞与Tfh为调节参数。chρ0为正数,表示初始误差界限;chρr表示性能函数初始变化方向;ρfh∞为ρfh(t)的稳态收敛值;Tfh表示ρfh(t)收敛至稳态值ρfh∞的设定时间。 类比速度跟踪误差性能函数参数选择条件式(18),chρ0需满足如下条件: (40) 式中:eh(0)为eh的初始值。高度跟踪误差性能函数式(38)同样可在设定时间Tfh处精确等于期望稳态值。下面将高度跟踪误差eh转化为无约束变量: eh=λhρfh(t)=S(εh)ρfh(t) (41) 其中:λh=S(εh)为关于εh的转换函数: (42) 转换误差εh通过反函数求解: (43) 根据转换误差εh设计期望飞行路径角γd[50]: (44) 式中:kP>0;rPh与HPh的定义为 (45) 若飞行路径角等于γd,则εh满足: (46) 故εh可指数收敛。则λh=S(εh)∈(-δhL,δhU)。 下面针对飞行路径角跟踪误差eγ设计考虑攻角约束的反步控制器,在实现eγ收敛的同时保证攻角处于允许工作区域内。 步骤1 对于高度子系统式(10)中的eγ动力学: (47) (48) (49) 其中:kγ>0。对虚拟控制αc0进行如下限幅处理: (50) 注意Aαc需满足:Aαc+max{ρfα(t)}≤Aα,其中ρfα(t)为下一步设计的攻角误差预定性能函数。 将αc通过固定时间滤波器可得αd0[51]: sigaF2[kα2(αc-αd0)] (51) 式中:τα为正时间常数;kα1,kα2≥1; 0 (52) 定义eα=α-αd与zα=αd-αc,则eγ满足: (53) 步骤2 对于攻角误差动力学: (54) 同样应用一致收敛观测器补偿扰动Δα: (55) -δαLρfα(t) (56) 类似式(12)与式(13),δαL,δαU∈(0, 1]。ρfα(t)的表达式为 ρfα(t)=aα3t4+aα2t3+aα1t2+cαρrt+cαρ0 (57) 其中:aα3、aα2与aα1的表达式为 (58) 其中:cαρ0、cαρr、ρfα∞与Tfα为调节参数。cαρ0为初始误差界限;cαρr表示性能函数初始变化方向;ρfα∞为ρfα(t)的稳态收敛值;Tfα为设定收敛时间。cαρ0需满足: (59) 其中:eα(0)为eα的初始值。将eα进行转化: eα=λαρfα(t)=S(εα)ρfα(t) (60) 其中:λα=S(εα)为关于εα的转换函数: (61) 转换误差εα通过反函数求解: (62) 因此,虚拟控制律Qc设计为 (63) 式中:kα>0;rPα与HPα定义为 (64) 将虚拟控制Qc通过固定时间滤波器可得滤波器输出信号Qd: sigaF2[kQ2(Qc-Qd)] (65) 式中:τQ>0;kQ1≥1;kQ2≥1。 定义eQ=Q-Qd与zQ=Qd-Qc,则攻角转换误差εα对应的动力学满足: (66) 步骤3 对于俯仰角速度误差动力学: (67) 应用一致收敛观测器补偿扰动ΔQ: (68) (69) 其中:控制参数kQ>0。则eQ的动力学为 (70) 定理2在虚拟控制律式(49)、式(63)和舵偏角控制指令式(69)作用下,高度子系统可以实现一致最终有界,同时攻角始终处于限定幅值式(11)之内。 证明:为子系统式(10)设计李雅普诺夫函数: (71) 结合式(53)、式(66)与式(70),可得Vh的导数满足: (72) 式中:Gγ0eγeα项满足 |Gγ0eγeα|≤|Gγ0||eγ||ρfαS(εα)|≤ ρfα|Gγ0||eγ||εα| (73) 将式(73)代入式(72)可得: (74) zα与zQ是固定时间滤波器跟踪误差,其满足: (75) (76) (77) 综合考虑多种情况,若参数选择满足: (78) (79) α=eα+αd≤|eα|+|αd|≤max{ρfα(t)}+ Aαc≤Aα (80) 因此攻角能够始终处于预先限定幅值式(11)内。□ 本节将约束预定性能控制器应用于吸气式高超声速飞行器中,验证跟踪性能约束与进气条件约束的满足情况。飞行器初始条件如表2所示。 表2 初始条件 速度与高度通道的阶跃指令为 Vc=2 407.92 m/s,hc=26 212.8 m 定义飞行器气动参数与结构参数的参数不确定度为[25] (81) 式中:ACr=20%;APr=10%。约束预定性能控制器的设计参数如表3所示。 表3 约束预定性能控制器的设计参数 以速度通道为例,下面给出设定时间性能函数的参数选择依据。根据式(14)可知δVL,δVU∈(0, 1],故选择δVU=1,δVL=1,表示将eV直接限定在由ρfV(t)与-ρfV(t)构成的界限内;ρfV∞表示速度跟踪误差的期望稳态收敛值,因为速度跟踪误差在控制器作用下能够实现高精度有限时间收敛,所以选择ρfV∞=10-3。cVρr表示性能函数的初始变化方向,当其为正数时性能函数初始增大,为负数时性能函数初始减小,因此cVρr决定了性能函数的初始收敛速度。因为速度跟踪误差eV的初始响应速度并无特殊要求,所以cVρr的选择较为灵活,故令cVρr=0。TfV为性能函数的期望收敛时间,这里设定为4 s。cVρ0表示性能函数的初始界限,需要满足式(18),这里eV(0)=-1 m/s,则计算式(18)的右端项可得:cVρ0>1,所以选择cVρ0=1.1。 场景A本场景将本文的约束预定性能控制器与2种控制器进行了对比仿真。一种为不考虑性能与进气约束的控制器,一种为文献[34]设计的预定性能控制器。第1种无约束控制器(Unconstrained Controller,UCC)未考虑速度与高度的跟踪误差约束,未对攻角跟踪误差进行预定性能处理也未对攻角虚拟控制进行限幅,剩余控制器部分与本文控制器相同;文献[34]采用传统预定性能函数:ρfV(t)=(cVρ0-ρfV∞)e-kρt+ρfV∞。控制器部分结合神经网络与滑模控制,文中仅考虑了性能约束,未考虑进气约束。为了与本文控制器单独对比新型设定时间性能函数的优势,本场景下的对比仿真修改文献[34]的控制器与本文相同,同样考虑攻角约束,只是采用不同的性能函数。其中,速度、高度、攻角跟踪误差的性能函数参数分别选择为:kVρ=0.5,khρ=0.15,kαρ=0.3。 场景A下的仿真结果如图2~图6所示。高超声速飞行器跟踪误差eV、eh与eγ的跟踪曲线如图2~图4所示。图2(a)与图3(a)对比了本文控制器(proposed)与无约束控制器的效果,曲线表明在无约束控制器作用下,速度与高度跟踪误差均超出了期望性能边界,而约束预定性能控制器则能够将跟踪误差有效限定在设定性能函数区域内。图2(b)、图3(b)与图4比较了本文控制器与对比仿真的效果。曲线显示了2种性能函数不同的收敛特性,对比仿真的性能函数仅能够以指数形式无限趋近于期望稳态收敛值,与之相比,本文设定时间性能函数能够在指定时刻快速精确收敛至期望稳态值,不仅收敛速度快,而且可灵活调节收敛时间。在不同性能函数作用下,本文的跟踪误差能够实现更快的收敛速度。图5与图6给出的是本文控制器作用下的速度与高度跟踪误差的转化误差变量与归一化变量。结果表明εV与εh均可快速收敛,且归一化变量λV与λh能够分别有效限定至预定界限(-δVL,δVU)与(-δhL,δhU)内。 图2 速度跟踪性能 (场景A) 图3 高度跟踪性能(场景A) 图4 飞行路径角跟踪性能(场景A) 图7给出的是攻角与俯仰角速度变化曲线,其中红色点划线为满足发动机进气条件的最大攻角值(αmax)。无约束控制器作用下的攻角在初始动态响应过程中超出了最大允许值,这将导致发动机熄火,推进系统瘫痪。与之相比,约束预定性能控制器作用下的攻角始终处于最大攻角值之下,能够满足发动机进气需求。图8给出的是飞行器的执行机构变化曲线,可见在约束预定性能控制器作用下,控制输入处于表1所列的允许边界内。而且,本文控制器相比UCC和对比仿真的最大控制量都要小,这表明本文控制器在实际应用中可以有效避免控制信号的幅值饱和,其原因在于设定时间性能函数中的参数cρ r能够调节性能函数初始变化方向,灵活调整状态量的初始收敛速率。图9与图10给出的是约束预定性能控制器的固定时间滤波器跟踪结果,滤波输出αd和Qd可分别以高精度跟踪输入信号αc和Qc。且图9显示,为了实现飞行攻角约束,攻角虚拟控制αc与滤波输出αd均被限幅不超过Aαc。图11显示了攻角跟踪误差与俯仰角速度跟踪误差,曲线表明攻角跟踪误差被有效限定在预定性能函数内。类似于速度与高度跟踪误差,本文控制器作用下攻角跟踪误差相比对比仿真同样可实现更快的收敛速度。图12说明攻角的转化误差变量εα可保持一致最终有界,归一化变量λα能够限定至预定界限(-δαL,δαU)内。 图8 燃油当量比与升降舵偏转角 (场景A) 图10 虚拟控制信号Qc的跟踪曲线 (场景 A) 图11 攻角与俯仰角速度跟踪误差 (场景 A) 图12 攻角跟踪误差的εα与λα (场景 A) 场景B本场景对飞行器进行100次蒙特卡洛打靶仿真,其中参数不确定度的定义如1.2节所示。实际值Pr与Cr均满足均匀分布规律。即飞行器的实际结构、气动、推力拟合参数满足: (82) 式中:ACr=40%;APr=10%; U(-1, 1)表示-1~1闭区间上的均匀分布。为了保证强不确定性扰动下控制器的鲁棒性,控制参数设定为:cαρ0=0.02,ρfα∞=0.05,kV=2,Tfh=25,kγ=kα=kQ=0.3,剩余参数与表3一致。 场景B的仿真结果如图13~图18所示,可见在考虑强不确定性参数摄动影响下,本文控制器仍然能够保证飞行器的稳定性,并同时满足跟踪误差的性能约束与攻角幅值约束。 图14 高度跟踪性能(场景B) 图15 飞行路径角跟踪性能(场景B) 图16 攻角与俯仰角速度(场景B) 图17 燃油当量比与升降舵偏转角(场景B) 图18 攻角与俯仰角速度跟踪误差(场景B) 本文针对受跟踪误差性能与发动机进气条件约束的高超声速飞行器控制需求,设计了约束预定性能控制器。 1) 对于跟踪误差性能约束,首先设计设定时间性能函数。相比传统方案,其能够保证性能函数在预先设定时刻精确等于稳态值,同时灵活调整函数初始收敛速率。然后将受约束的跟踪误差进行无约束转化,通过控制转化误差有界可实现原始跟踪误差的预定性能约束。 2) 在高度子系统中,为指令滤波反步法设计了新型固定时间滤波器,相比结合传统低通滤波器,高度跟踪误差能够在相同时间常数下实现更高的收敛精度与更快的响应速度。 3) 通过在反步控制器中对攻角虚拟控制进行限幅处理,并对攻角跟踪误差执行预定性能控制,能够满足攻角幅值约束。 4) 对比无约束控制器,本文的约束预定性能控制器能够同时满足跟踪误差性能约束与攻角约束,综合保证系统瞬态与稳态性能,始终满足吸气式超燃冲压发动机的进气需求。

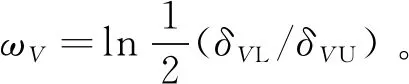
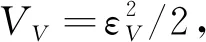
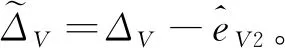
2.2 高度子系统指令滤波反步预定性能控制器





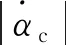



3 仿真分析






4 结 论

