基于传递函数特征的机械结构故障诊断方法新进展
李全坤,景兴建
1. 西北工业大学 动力与能源学院,西安 710129
2. 香港理工大学 机械工程系,香港 999077
航空航天工程中的机械结构经常遭受线性故障(腐蚀和剥落等)和非线性故障(螺栓松动和疲劳裂纹等)[1-4]。例如,飞机结构中焊接位置经常出现裂纹和腐蚀故障,火箭结构中易产生疲劳裂纹和断裂等故障,卫星结构连接处往往出现螺栓松动等故障。这些故障不仅影响机械结构的完整性而且可能危害使用者和维修者的生命安全。因此,故障诊断在提高机械结构的可靠性,减少使用者的维修成本以及优化维护团队的维修策略等方面是非常重要和必要的。
故障诊断的主要目的是估计机械结构在各种载荷环境和工况条件下的状态,总共可以分为环境评估、数据获取、特征提取和故障诊断4个过程[5-8]。环境评估过程主要是估计待测机械结构的周围环境及工况条件,数据获取过程主要涉及传感器类型和安装、数据测量和预处理,下一个过程是运用各种算法提取故障结构的故障特征,最后一个过程是利用提取的故障特征实现故障的诊断。对于最后的故障诊断过程,学者Rytter[9]将其划分为故障识别(故障存在与否)、故障定位(故障位置信息)、故障评估(故障严重程度)及寿命预测(结构剩余寿命)4个阶段。4个阶段的层次关系非常清楚,后一级层次需要前一级层次的所有信息。
基于振动的故障诊断特征是结构属性(质量、阻尼和刚度)的函数,故障引起的任何属性变化都会反映到相应的故障特征和识别因子当中,因此可通过故障特征和识别因子的变化判断结构中故障的情况,这是故障诊断方法所依据的基本原理[10-15]。尽管采集的信号都是原始时域振动信号,但频域的故障特征和识别因子可以提供更加直观和有效的结构故障信息[10-15]。常用的频域故障特征包括模态属性、频响函数、输出频谱以及传递函数[16-17]。与其他特征相比起来,传递函数具有明显的优点。例如,传递函数只由输出响应计算得到,这就避免了复杂的模态分析和输入激励的测量。传递函数在较宽的频率范围内包括模态参数(固有频率和模态振型)及空间信息,因此它对于结构局部的故障变化更加的灵敏。
对于机械结构中经常出现的线性故障(腐蚀和剥落等)和非线性故障(螺栓松动和疲劳裂纹等),现有文献提出了大量的基于线性或非线性传递函数的故障诊断方法。这些方法主要针对故障诊断的前2个阶段,即故障识别和故障定位,同时方法的有效性和实用性也通过大量的仿真和实验得到了充分的证明[8-15,18-20]。但是,目前还并没有一篇完整的综述性文章系统性地解释这些方法的基本原理及充分地对比这些方法的优缺点。因此,本文的主要目标是对基于线性或非线性传递函数的机械结构故障诊断方法的进展进行研究,通过理论分析和实际实验结果解释它们的基本原理、操作流程、优点以及局限性,以期为现有故障指示因子灵敏度的提高及现有方法在其他复杂机械结构中的运用提供支持。
全文6节的主要内容安排如下:第1节按照从线性到非线性的思路回顾了各种基于传递函数的故障诊断方法。第2节介绍了常用于分析机械结构动力学特性的链式多自由模型。第3节解释了基于一般线性和非线性传递函数故障诊断方法的基本原理。第4节阐述了基于Volterra级数传递函数的故障诊断方法的基本原理。第5节通过实验实例展示了各种方法的优缺点。第6节总结了本文的结论、创新点及贡献。
1 诊断方法文献综述
传递函数通常被定义为结构中2个不同位置输出频谱的比值。因为输出频谱可以是线性的也可以是非线性的,基于传递函数的故障诊断方法相应地分为线性和非线性方法[20]。线性方法主要考虑线性故障(结构线性参数的扰动),因此初始线弹性结构在结构产生故障后依然保持线弹性行为。与线性方法不同,非线性方法主要考虑非线性故障(额外的非线性引入),因此初始线弹性结构在故障发生后表现出非线性的行为和特性。在以下各节中,文献中大量基于线性和非线性传递函数诊断方法按照一般线性方法、一般非线性方法、基于广义频响函数方法和基于二阶输出频谱方法的顺序依次进行介绍和回顾。
1.1 一般线性方法
传递函数作为故障识别特征最早在文献[21]中被使用,之后,它被大量地运用于基于异常检测算法的故障识别方法中。在文献[22]中,传递函数被用于训练人工神经网络,模型结果被用于三自由度系统中刚度系数减小的识别。与此类似,文献[23]使用传递函数作为多层感知神经网络的输入,训练结果被分别运用于夹层梁结构中剥落故障和钢架结构中螺栓连接松动故障的识别。结合传递函数和马氏距离,文献[24]识别了三自由度仿真结构中刚度系数的减小,之后,文献[25]通过有限元悬臂结构中刚度系数下降的辨识验证了方法的有效性。除了结合异常检测算法,一些直接运用传递函数的频域故障指示因子和置信度准则同样被运用于结构故障诊断。运用柔性压电薄膜传感器,文献[26]运用健康管路和故障管路的传递函数比值识别管路阻塞故障。对于风机涡轮叶片的状态监测,文献[27]采用基本结构和故障结构之间传递函数的相对误差为监测指标。基于模态置信准则,两端固支梁中单个刚度故障得到了有效的诊断[28]。在文献[29]中,学者通过传递函数定义了识别和相关故障评估因子,并运用其识别了有限元梁模型中的故障单元。在此基础上,改进的识别和相关故障评估因子被用于风力发电机械的在线状态监测[30]。
以上文献中方法直接使用传递函数并且没有解释传递函数作为故障特征的基本原理和性质。因此,大多数方法只能判断故障的出现(阶段1)及提供少量的故障位置信息(阶段2)和故障程度信息(阶段3)。根据文献[31]中系统性介绍的多自由度模型中频响函数的性质,文献[32-33]总结了多自由度模型中存在质量改变和刚度减少时传递函数的变化规律,然后设计了相应的磁感应式移动监测系统用于钢架结构中螺栓松动故障的诊断。文献[34]定义了传递函数矩阵,并通过统计故障结构和健康结构之间传递函数最大值的个数判断故障位置。只运用故障结构中传递函数,文献[35]提出了新的故障指示因子并用于简支桥梁中抗剪连接件故障。对于隧道结构中存在的弹性模量和墙壁厚度下降故障,文献[36]提出了基于对数传递函数的故障指示因子。通过汽车-桥梁耦合系统测量和计算传递函数,文献[37]提出了针对桥梁故障的6个传递函数相关的指示因子。
为减小噪声对故障指示因子的影响,学者们提出使用自功率谱和互功率谱定义传递函数[38-39],然后提出了相关的基于距离和相似性测量的故障指示因子[40-43]。比如,城市街区距离、欧几里得距离、马氏距离、余弦相似测量以及皮尔逊相关系数等。除了基于功率谱的传递函数,基于功率模式形状的传递函数也被用于梁中刚度系数减小的判断[44]。与文献[34]中方法类似,基于功率谱的传递函数矩阵被定义并被用于悬臂梁中螺栓松动故障的监测[45]。借鉴模态振型和频响函数中经常使用的曲率概念,文献[46]定义了曲率传递函数并识别和定位了仿真梁中的单元故障。基于相干函数的概念,文献[47]提出了传递函数相干的概念并定义了2个崭新的故障指示因子用于3层建筑结构中故障的识别。结合传递函数相干函数和分层聚集算法、余弦相似测量和距离测量算法,文献[48]定位了自由梁中不同深度的缺口故障。考虑到傅里叶变换在处理数据时可能出现泄漏和边界效应等问题,文献[49]运用小波分析处理数据并运用基于小波频谱的传递函数和故障指示因子辨识钢架结构中故障单元。
以上文献中方法通过不同类型线性传递函数定义了大量的基于传递函数的故障识别因子(表1),但这些方法都只考虑了故障对结构的线性影响,也就是无论是健康结构还是故障结构,结构都只存在线性的动力学行为。对于线性结构而言,它们的动力学特性较为简单,理论分析相对较容易,但这些优点也会在一定程度上阻碍这些方法的进一步应用和发展。例如,疲劳裂纹常使结构表现出双线性特性,螺栓松动常导致连接处部件的滑移和摩擦。因此,只考虑线性故障和线性结构的诊断方法可能会误判结构的状态或漏判结构中存在的故障。

表1 一般线性传递函数方法总结
1.2 一般非线性方法
考虑到非线性故障会引起结构非线性的动力学行为和特性,某些诊断方法运用非线性输出频谱定义传递函数。通过模拟线性和非线性故障为作用于结构的内部回复力,文献[50]分析了三自由度非线性系统中传递函数的性质,提出了基于健康结构和故障结构之间传递函数的相对变化量的故障指示因子。之后,文献[50]中的方法陆续被用于结构中螺栓松动故障和非线性间隙的判断[51]。在此基础上,文献[52-54]利用不同的对数算法正规化处理了文献[50-51]中的传递函数和故障指示因子,并成功定位了3层建筑结构和汽车悬架结构中故障。同时考虑激励频率和高频处的非线性工作变形模态,文献[55]运用传递函数工作变形模态和新的故障指示因子定位裂纹引起的结构不连续性。
1.3 基于广义频响函数方法
利用Volterra级数表示非线性系统,学者们通过从非线性输出谱中分解出来的各阶输出频谱定义了Volterra型传递函数。利用广义频响函数,传递函数被定义为多自由度系统中广义频响函数的比值并用于非线性结构中非线性单元的定位[56]。之后,文献[57]利用单激励多频率的输入方法优化了广义频响函数估计算法,简化了传递函数的计算过程。为了避免广义频响函数复杂的分解算法,学者们提出了双正弦激励法计算传递函数,完成了梁结构中故障的识别[58]。在此基础上,文献[59]提出了针对输电线路中接地故障的诊断方法,文献[60]提出了可同时诊断线性和非线性故障的系统性方法,文献[61]提出了液压管路中裂纹故障的定位方法。在分析广义频响函数和非线性输出谱相互关系的基础上,文献[62]直接利用输出谱定义传递函数,提出了包含4个步骤的可依次判断故障数量的故障诊断方法。
1.4 基于二阶输出频谱方法
为进一步提高Volterra型故障识别因子的灵敏度,学者们提出只利用前2阶输出频谱定义传递函数。在文献[63-64]中,作者提出了一个有效的不需要知道结构最大的非线性阶次的输出频谱估计方法,估计的基于二阶输出频谱的传递函数被分别用于梁中裂纹和卫星结构中螺栓松动故障的识别[65-66]。在此基础上,文献[67]考虑和消除了结构固有材料和边界非线性对基于二阶输出频谱的传递函数的影响。为了克服以往基于传递函数诊断方法中故障位置信息不明确的问题,文献[68]结合局部结构参数调整法和二阶输出频谱型传递函数,提出了只通过3个传感器判断故障的有效方法。稍后,此方法成功扩展到管路和钢架等环形结构中螺栓松动故障的识别[69]。考虑结构中同时存在初始故障和严重故障,文献[70]结合局部结构参数调整法和二阶输出频谱型传递函数提出了可依次诊断这2种故障的系统性方法。
与1.1节中线性方法相比,非线性方法的最大特点是考虑了故障非线性的影响并且模拟故障为非线性回复力。如表2所示,所有非线性方法都可同时识别和定位非线性故障。文献[50-55]中的一般非线性方法只利用激振力频率处的响应,忽略了故障引起的高阶谐波响应。因此这类方法难以提供高灵敏度的故障指示因子。在基于广义频响函数传递函数的诊断方法中[56-62],非线性输出频谱被分解为不同的阶次,相应的故障指示因子被用来识别和定位线性及非线性故障。为提高故障指示因子的灵敏度,文献[65-70]只利用前2阶输出频谱计算传递函数,提出了基于二阶输出频谱传递函数的故障指示因子。理论分析和实验结果证实直接利用线性或者非线性传递函数的诊断方法只能给出大概的故障位置信息(故障位于激励位置和最后故障位置之间区域)[21-62,65-67],而基于局部结构参数调整法和二阶输出频谱型传递函数的诊断方法可通过3个传感器有效的判断局部故障的准确位置[68-70]。

表2 非线性传递函数方法总结
2 结构多自由度模型
如图1所示,连续机械结构一般离散为由质量-阻尼-弹簧单元组成的多自由度(Multi-Degree-of-Freedom, MDOF)模型[18, 31, 50, 56, 65],图中m1~mn、ci~cn、k1~kn分别为质量、阻尼和刚度系数;x1(t)~xn(t)为输出响应;u(t)为输入激励。假设所有质量只在水平方向运动,固定边界约束施加于模型的最左边,单个简谐激励作用于左边第1个质量点。根据结构中是否存在线性故障或非线性故障,相应的连接单元被模拟为线性单元或非线性单元。
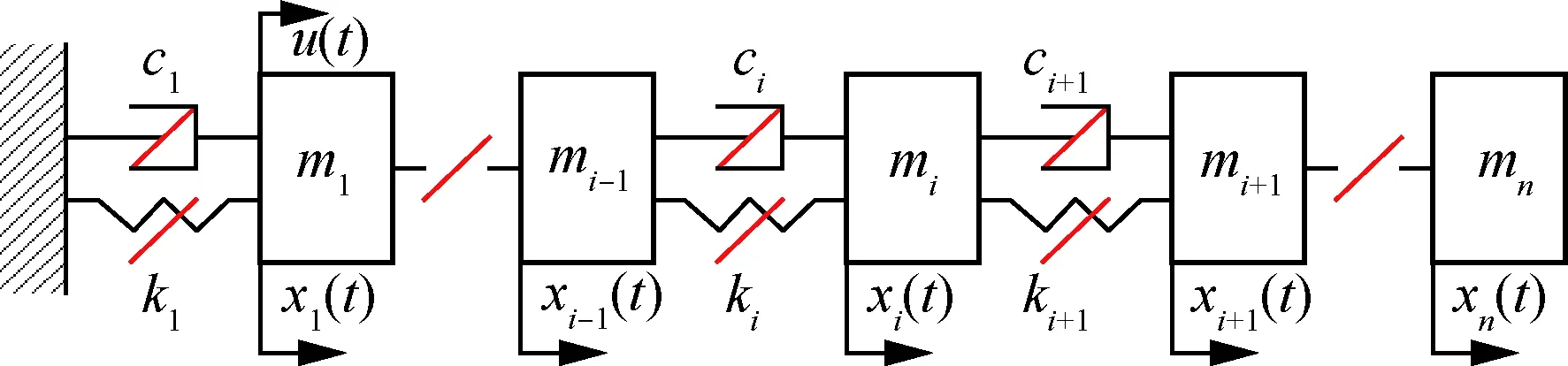
图1 离散链式多自由度模型
多自由度模型运动微分方程可表示为[71-75]
(1)
或者更加紧凑的形式:
(2)


(3)
式中:Δci、 Δci+1、 Δki和 Δki+1分别为质量mi附近线性故障引起的阻尼系数和刚度系数的扰动。

(4)

综上所述,存在线性或者非线性故障的机械结构可离散为具有线性或者非线性连接单元的链式多自由度模型,其动力学特性可通过带有非线性回复力的动力学运动微分方程描述。
3 基于一般传递函数诊断方法的原理和流程
1.1节和1.2节分别介绍了运用一般线性和非线性传递函数的诊断方法[21-55]。在这些方法中,传递函数可通过输出频谱[21, 31]、功率频谱[38, 45]和小波频谱[49]等定义,同时故障指示因子可通过奇异值分析[24]、置信准则[30]、传递函数差异[32]和传递函数积分[50]等建立。这些方法的共同特点是只有激振力频率处的线性或非线性输出频谱被用来定义传递函数,各种方法的基本原理和操作流程类似。为帮助读者更好地理解这些方法,这类方法的基本概念、原理和流程现介绍和解释如下。
3.1 一般输出频谱
通过对运动微分方程(2)两端运用傅里叶变换,复频域运动微分方程可表示为[50]
(5)
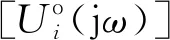
如果系数矩阵的逆矩阵可表示为H(jω)=A(jω)-1,则多自由度模型的一般输出频谱可表示为
(6)
从方程(6)中可以看出,如果多自由度模型中没有非线性故障,模型为线性系统,因此只有线性响应存在。相反,如果多自由度模型中存在非线性故障,额外的非线性阻尼和刚度系数将会引入到结构连接单元中,使结构中存在非线性响应。
3.2 一般传递函数和故障指示因子
扩展频域运动微分方程(5),同时方程两端同时除于Xi(jω)得可得
[-m1ω2+jω(c1+c2)+(k1+k2)]-(jωc2+
jω(ci+ci+1)+(ki+ki+1)]-(jωci+ki)·
(-mnω2+jωcn+kn)-(jωcn+kn)·
(7)
(8)
将方程(8)代入方程(7)可得
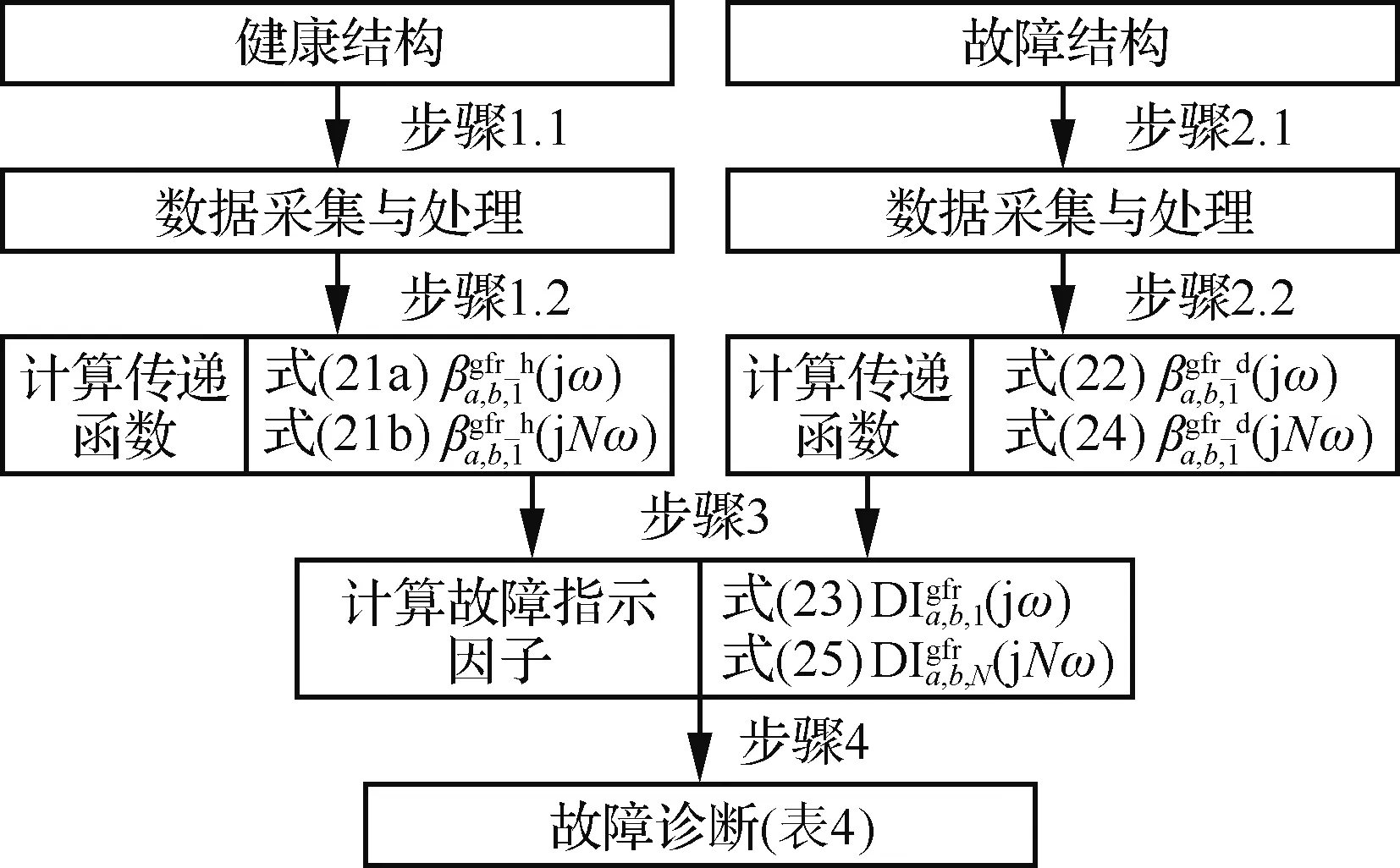
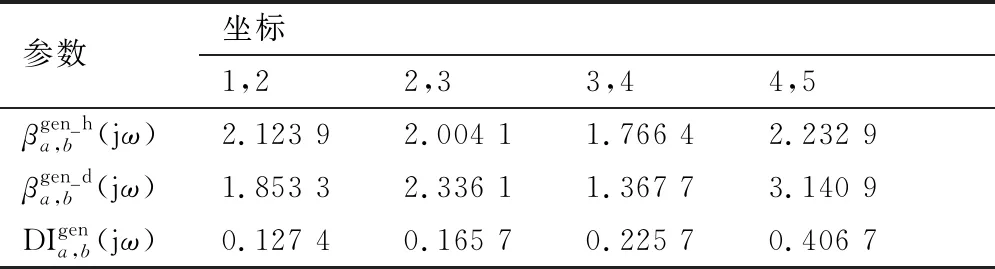
2≤i (9) 方程(9)表明传递函数为结构局部质量、阻尼、刚度系数和故障引起的线性和非线性回复力的函数,因此其可以用于估计局部结构的状态。 如果结构处于健康状态,故障引起的所有线性和非线性回复力为零。因此,方程(9)可改写为 (10) 式中:带有上标gen_h和h的参数表明其由健康结构获得。 如果结构处于故障状态,并假设线性或者非线性故障位于多自由度模型中质量mp和mq之间,方程(9)可改写为 ⋮ ⋮ (11) 式中:带有上标gen_d和d的参数表明其由故障结构获得。 1≤a,b≤n,a≠b (12) 一般传递函数及基于一般传递函数的故障指示因子的性质总结于表3中。 表3 一般传递函数和指示因子 如图2所示,基于一般传递函数的诊断方法主要包括4个步骤。健康结构和故障结构的传递函数分别在步骤1和步骤2计算得到。运用方程(12),故障指示因子在步骤3计算得到。最后,结构中是否有故障根据表3中总结的故障指示因子属性判断。这类方法中其他更加复杂的故障指示因子和操作流程可参照图3中流程得到。 图2 一般传递函数诊断方法流程 图3 基于广义频响函数传递函数诊断方法流程 除了直接运用线性或者非线性输出频谱定义传递函数,学者通过研究发现通过Volterra 型输出频谱定义传递函数可得到更加灵敏的故障特征和指示因子。1.3节和1.4节分别回顾了相应的基于广义频响函数传递函数[56-62]和基于二阶输出频谱传递函数得诊断方法[65-70]。与上文中基于一般传递函数故障诊断方法只利用基频处输出频谱不同,基于Volterra 型传递函数诊断方法运用频率范围内各阶输出频谱定义传递函数、故障特征和指示因子。和第3节内容类似,基于Volterra 型传递函数诊断方法的基本概念、原理和流程分别介绍如下。 因为带有非线性故障的结构为非线性系统,其输出响应根据Volterra级数可表示为[76-80] (13a) (13b) 当作用于结构(图2)的单个简谐激励为 u(t)=Aejωt (14) 式中:A为幅值。 质量mi相应的输出响应可表示为 (15) 将方程(14)和方程(15)代入方程(2),然后提取方程两边项ejNωt(N≥1)前系数可得 A(jω)n×n[Hi,1(jω)]n×1=[Ui(jω)]n×1+ (16a) (16b) 利用逆矩阵B(jNω)=A(jNω)-1(N≥1),多自由度模型的Volterra型输出频谱可表示为 [Hi,1(jω)]n×1=B(jω)n×n([Ui(jω)]n×1+ (17a) (17b) 方程式(17)包括2部分。第1部分为第1阶输出频谱,代表结构的线性输出。第2部分为由故障引起得的结构高阶非线性输出频谱。和方程式(6)中的结果类似,当结构处于健康状态或只存在线性故障时,结构为线性系统,因此只有线性输出频谱的存在。但是,当结构中存在非线性故障时,额外的非线性高阶输出频谱存在于系统中。 广义频响函数定义为Volterra核函数的傅里叶变换。一阶广义频响函数就是线性系统中常用的频域响应函数,二阶以上广义频响函数代表非线性系统中非线性对结构的影响[56-62]。 4.2.1 基于广义频响函数传递函数及指示因子 扩展频域运动微分方程(16),方程两端同时除以Hi,N(jω,…,jω)(N≥1),得 [-m1ω2+jω(c1+c2)+(k1+k2)]-(jωc2+k2)· [-miω2+jω(ci+ci+1)+(ki+ki+1)]-(jωci+ (18a) (18b) 1≤a,b≤n,a≠b,N≥1 (19) 因此,方程(18)可改写为 (20a) 2≤i (20b) 当结构处于健康状态时,故障引起的所有线性或非线性Volterra型回复力为零,因此方程(20)可改写为 (21a) (21b) 式中:带有上标gfr_h或h的参数代表其来自于健康结构。 当线性故障位于结构质量mp和mq之间时,方程(20a)变为 ⋮ ⋮ (22) 式中:带有上标grf_d或d的参数代表其来自于故障结构。 1≤a,b≤n,a≠b (23) 如果非线性故障存在于结构质量mp和mq之间,方程(20b)变为 p≤i≤q (24) 1≤a,b≤n,a≠b,N≥2 (25) 方程(23)和方程(25)中基于广义频响函数的故障指示因子的性质归纳如表4所示。 表4 基于广义频响函数传递函数和指示因子 4.2.2 方法操作流程 和图2中基于一般传递函数诊断方法的操作流程类似,基于广义频响函数传递函数诊断方法同样具有4个步骤。健康结构和故障结构中基于广义频响函数传递函数分别计算于步骤1和步骤2。在步骤3中,故障指示因子分别通过方程(23)和方程(25)计算得到。最后,根据表4中故障指示因子的属性,线性或非线性故障可通过观察相应指示因子的数值得到。其他基于广义频响函数传递函数的操作可参考图4中步骤得到。 因为二阶输出频谱只由结构二阶非线性决定并且不受结构高阶非线性的影响,所以基于二阶输出频谱传递函数可显著提高故障指示因子的灵敏度[65-70]。文献[65-67]中方法与文献[56-62]中介绍的方法类似,最大的区别在于文献[65-67]中方法考虑了结构固有材料和边界非线性对故障特征和指示因子的影响。在此基础上,文献[68-70]中方法利用基于二阶输出频谱传递函数和局部结构调整参数法提供了更加准确的局部故障位置信息。 4.3.1 基于二阶输出频谱传递函数及指示因子 只考虑方程(16)中前2阶输出频谱并提取质量mi(2≤i≤n-1)的运动微分方程, 运用方程(19)中相似的传递函数定义得 [-miω2+jω(ci+ci+1)+(ki+ki+1)]-(jωci+ (26a) [-mi(2ω)2+j2ω(ci+ci+1)+(ki+ki+1)]- (26b) [-miω2+jω(ci+ci+1)+(ki+ki+1)]= (27a) (27b) 式中:带有上标soo_h的参数表示其来自于健康结构。 对健康结构运用文献[68-70]中提出的局部结构参数调整法可得到和方程(27)类似的方程: [-miω2+jω(ci+ci+1)+(ki+ki+1)]= (28a) (28b) 其中:带有上标′的参数表示其来自于被运用了局部结构参数调整法的健康结构。 观察方程(27)和方程(28),方程左边相同的项可以被消掉,2个基于传递函数的故障特征可表示为 (29a) (29b) 当结构中质量mi附近存在线性故障时,以下方程成立: [-miω2+jω(ci+ci+1)+(ki+ki+1)]=(jωci+ (30) 式中:带有上标soo_d和d的参数表示其来自于故障结构。 通过方程(28a)和方程(30),针对于线性故障的基于二阶输出频谱传递函数的故障特征可表示为 (31) 2≤i≤n-1 (32) 当结构中质量mi附近存在非线性故障时,以下方程成立: (33) 通过方程(28b)和方程(33),针对非线性故障的基于传递函数的故障特征可表示为 (34) 2≤i≤n-1 (35) 观察方程(32)和方程(35),针对于线性和非线性故障的基于二阶输出频谱传递函数和识别因子的性质归纳如表5。 表5 基于二阶输出频谱传递函数和指示因子的性质 4.3.2 方法操作流程 根据所定义的来自于参考结构和故障结构的故障特征,基于二阶输出频谱传递函数和局部结构调整参数法的诊断方法的流程总结如图4所示。和3.3节和4.2.2节中的操作流程相比,基于二阶输出频谱传递函数和局部结构调整参数法的诊断方法具有更多的步骤。在步骤1中,健康结构中的传递函数通过方程(27)计算得到。在步骤2中,局部结构参数调整法运用于健康结构,额外的传递函数通过方程(28)得到。在步骤3中,用于参考的故障特征通过方程(29)计算得到。在步骤4中,故障结构中的传递函数通过方程(30)和方程(33)计算得到。运用方程(31)和方程(34),用于诊断的故障特征在步骤5中计算得到。在步骤6中,线性或者非线性故障指示因子通过方程(32)和方程(35)分别计算得到。最后,质量mi附近是否存在线性或者非线性故障通过表5中的性质在步骤7中得到。 图4 基于二阶输出频谱传递函数诊断方法流程 前文对各种基于传递函数故障诊断方法的基本原理和操作流程进行了详细的解释和阐述。为进一步直观地展示各种方法的有效性、优点及局限性,一些仿卫星结构中螺栓松动故障的实验诊断结果在本节进行分析和解释。 实验中所采用的仿卫星结构如图5所示。仿卫星结构主要由铝合金主体和太阳板通过螺栓连接[70]。结构上端通过弹簧悬挂于龙门支架,下端连接激振器模拟激励输入,振动信号通过三轴加速度传感器采集。传感器(编号Sc)安装于激振器输出轴作为输入信号和控制信号,其余5个传感器(编号依次为S1,S2,S3,S4和S5)沿振动传递路径安装于卫星结构形成传感器链路。根据文献[81]的研究结果,形成的传感器链路可以被看作为具有多自由度的虚拟梁结构并被用于结构中相应螺栓状态的估计。在局部结构参数调整法中,额外的质量(25 kg)施加于结构顶端(虚拟梁末端)。输入激励为正弦信号u(t)=Acos(2πft),其中幅值范围为0.34 g~0.69 g,步长为0.05 g,频率为8 Hz和16 Hz。 图5 实验仿卫星结构 如表6所示,结构故障通过拧松主体上相应位置的螺栓连接来实现。实验中总共考虑了3种结构状态。对于结构参考状态,设定结构中不存在螺栓松动故障。结构故障状态1(案例1)中单个初始螺栓松动故障位于传感器S3和S4之间,螺栓扭矩从4 N·m下降至0.5 N·m。初始故障主要引起结构中非线性参数变化,因此案例1主要模拟结构中存在非线性故障时的情况。结构故障状态2(案例2)中单个严重螺栓松动故障位于传感器S3和S4之间,螺栓扭矩从0.5 N·m下降至0 N·m。严重故障主要引起结构中线性参数变化,因此案例2主要模拟结构中存在线性故障时的情况。 表6 实验方案设计 5.2.1 案例1 在这个案例中,结构中存在固有材料和边界非线性,同时单个初始螺栓松动故障位于传感器S3和S4之间。图6中,u为输入,S1~S5为传感器位置,各种方法的实验结果如表7~表9所示[70]。 图6 案例1示意图 表7 案例1一般传递函数方法结果[70] 表9 案例1基于二阶输出频谱传递函数方法结果 5.2.2 案例2 和案例1中类似,案例2中结构同样考虑结构固有非线性的影响,同时单个严重螺栓松动故障位于传感器S3和S4之间。各种方法的实验结果如表10 所示[70]。 图7 案例2示意图 表10 案例2一般传递函数方法结果[70] 表11 案例2基于广义频响函数传递函数方法结果 表12 案例2基于二阶输出频谱传递函数方法结果 以上实验结果清楚地展示了不同故障诊断方法的优点及局限性。 1) 基于一般传递函数的诊断方法原理简单,但传递函数易受附近区域条件的影响,同时方法忽略了结构中固有材料和边界非线性的影响。因此,这类方法只能提供故障的大概位置信息,并且难以区分线性和非线性故障。 2) 尽管基于广义频响函数传递函数的诊断方法可以有效地区分线性和非线性故障,但这类方法和基于一般传递函数的诊断方法类似,诊断结果依然受传递函数性质的限制,难以提供更加确切的故障位置信息。 3) 和前面2种方法相比,基于二阶输出频谱传递函数和局部结构参数调整法的新诊断方法操作流程更加复杂,但实验结果表明这类方法不仅可以区分线性和非线性故障,而且可以给出比较精准的故障位置信息。 总的来说,从基于一般传递函数的诊断方法、基于广义频响函数传递函数的诊断方法到基于二阶输出频谱传递函数和局部结构参数调整法的诊断方法,操作流程变得越来越复杂,但诊断的故障形式和位置信息越来越可靠和准确。 本文对基于线性和非线性传递函数的故障诊断方法进展进行了系统性的研究和回顾,通过多自由度模型解释了各种方法的基本原理和使用流程,通过具体的仿卫星结构中螺栓松动故障的诊断比较了各种方法的优缺点。具体的对比分析结果如表13所示。 表13 基于传递函数方法比较结果 本文的主要结论、创新点及贡献归纳如下。 1) 根据传递函数定义中所使用的不同类型输出频谱,将基于传递函数的故障诊断方法分为线性方法和非线性方法两大类并对其进展进行了分别的归纳和研究。线性方法中主要考虑线性故障类型[21-49]而非线性方法中主要考虑非线性故障类型[50-70]。 2) 介绍了多自由度模型中模拟线性和非线性故障的线性和非线性阻尼弹簧单元以及如何通过带有额外回复力的微分运动方程来描述结构的动力学特性[18, 31, 50, 56, 65]。 3) 在一般传递函数的诊断方法中,激振力频率处的线性和非线性输出频谱被用来定义传递函数[21-55]。通过理论分析和实验结果验证了这类方法可准确识别故障的出现,但不能判断故障的类型和位置。 4) 运用Volterra级数理论,基于广义频响函数传递函数的诊断方法使用各阶广义频响函数定义传递函数和相关故障指示因子[56-62]。通过理论分析和实验结果验证了这类方法可有效地区分线性和非线性故障但不能提供准确的故障位置信息。 5) 在基于二阶输出频谱传递函数的诊断方法中,前2阶输出频谱被用来定义传递函数。结合局部结构参数调整法,更加灵敏的故障指示因子被用来估计局部故障的位置信息[68-70]。通过理论分析和实验结果验证了这类方法不仅能判断故障的类型而且可以给出准确的故障位置。 6) 在本文研究结果的基础上,基于线性和非线性传递函数诊断方法在以下方面需要进一步的研究和学习。比如,研究能提供故障严重程度和预测结构剩余寿命的故障指示因子。研究现有故障诊断方法在其他复杂结构(环形和平板结构等)中的扩展和运用。

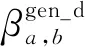
3.3 方法操作流程

4 基于Volterra型传递函数诊断方法的原理和流程
4.1 Volterra型输出频谱

4.2 基于广义频响函数传递函数诊断方法









4.3 基于二阶输出频谱传递函数诊断方法










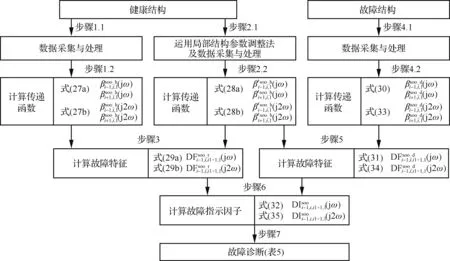
5 实验案例
5.1 实验方案介绍


5.2 实验结果分析

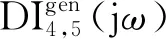







5.3 总 结
6 结 论


