卸荷条件下岩石Ⅰ型动态应力强度因子变化规律

李 欣，张振南

（上海交通大学船舶海洋与建筑工程学院，上海200240）

摘要：利用数值模拟软件ANSYS，分析卸荷条件下裂纹尖端Ⅰ型动态应力强度因子（DSⅠFs）变化规律及其影响因素，研究岩石内部裂纹动态起裂行为。结果表明：围压及其卸荷速率越大，DSⅠFs峰值越大，卸荷产生的动态效应越明显，轴压对卸荷动态效应无影响；瞬态卸荷时，DSⅠFs 最大值出现在卸荷后的持续阶段，存在滞后效应；卸荷过程中随内部应变能的释放，DSⅠFs 时程曲线呈衰减效应；围岩刚度对卸荷条件下的DSⅠFs 有显著影响，围岩刚度相对于岩爆体越小，DSⅠFs 峰值越大，动态效应越明显；高卸荷速率初期，起裂韧度增率大于DSⅠFs增率，裂纹不会立即起裂，随卸荷时间的增加，裂纹发生起裂。

关键词：裂隙岩石；瞬态卸荷；动态应力强度因子；岩爆；Ⅰ型裂纹

中图分类号：TU 413.3文献标志码：Adoi：10.3969/j.issn.1671-7872.2021.04.011

深部岩石处于高地应力状态，内部储存着很高的应变能，在受到工程开挖以及爆破施工扰动后，内部积聚的应变迅速释放，会导致岩爆发生，造成重大的经济损失甚至人员伤亡。岩爆的发生源于岩石内部应变能驱动下的裂纹失稳扩展。关于裂纹如何扩展已有较多研究，但多是加载条件下的岩石动态裂纹扩展，岩爆过程是卸荷条件下动态裂纹失稳扩展的过程，这与加载条件下的裂纹扩展不同。

卸荷条件下岩石内部裂纹的动态扩展是一个复杂的问题。根据断裂力学理论，当动态应力强度因子（dynamic stress intensity factors，DSⅠFs）达到动态起裂韧度时，裂纹开始扩展，扩展过程受制于动态止裂韧度等因素。围绕岩石动态断裂韧度问题，Wang等利用分离式霍普金森杆径，采用普适函数结合实验-数值法确定了中心直裂纹平台巴西圆的动态起裂和扩展韧度；杨井瑞等使用实验-数值-解析法测定了压缩单裂纹圆孔板（single cleavage drilled compression，SCDC）试样起裂韧度和扩展韧度，得出砂岩动态起裂韧度随动态加载率的增大而增大；张财贵等采用裂纹扩展计监测动态载荷下裂纹尖端起裂、扩展和止裂的动态全过程，首次测出SCDC试样的Ⅰ型动态止裂韧度。以往对于卸荷条件下裂纹尖端应力强度因子的研究主要是针对准静态过程。实际上，地下隧道或煤矿爆破开采时，卸荷时间为数毫秒到几百毫秒，会引起强烈的动态效应。卸荷条件下裂尖DSⅠFs 求解极其复杂，很难得到理论结果，开展的相关实验多以动态加载为主，而岩爆实际是一卸荷过程，与加载有很大区别。鉴于此，利用数值模拟软件对裂尖DSⅠFs 进行求解，探讨不同影响因素下Ⅰ型DSⅠFs的变化规律。

图1 J积分路径Fig.1 J integral path

1 动态应力强度因子计算方法

1.1 相互作用积分法

相互作用积分法源于

J

积分。

J

积分的计算公式为

式中：

Γ

为

J

积分路径；

n

为积分路径

Γ

单位外法向向量；

σ

为真实场中的应力；

μ

为真实场中的位移；

i

,

j

,

k

= 1,2,3；

W

为弹性应变能密度；

δ

为克罗内克符号。由辅助场引起的

J

积分为

对于线弹性材料，假设材料应力、应变和位移满足叠加原理，通过叠加真实场和辅助场可得

式中

I

为真实场与辅助场的相互作用积分，其表达式为

式中

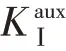
Ⅰ

和

Ⅰ

分别为第一次和第二次求得的相互作用积分。

1.2 验证算例

对于裂纹DSⅠFs 研究，最为经典的是动态断裂Chen 问题，Lin 等采用相同的方法对Chen 问题进行复算。为验证卸荷命令流的可行性及精确度，对经典动态断裂Chen 问题进行验证，采用Lin 等的计算结果作为对照。计算模型及裂纹尺寸如图2，

H

为平板长度，

B

为平板宽度，

a

为裂隙半长，

P

(

t

)为阶跃冲击荷载。

图2 中心穿透裂纹板几何模型及载荷Fig.2 Geometric model and load of center penetrating crack plate

选用的矩形薄板为PLANE183 单元，单元类型为平面应变型；考虑到奇异性，设置裂纹尖端节点为1/4节点；裂纹中心穿透裂纹矩形板受轴向拉伸阶跃冲击载荷，

P

(0) =10 MPa，荷载作用时间

t

=14 μs；在进行裂纹尖端应力强度因子动态分析时，取时间步长Δ

t

=0.01μs。为方便比较冲击荷载作用下的裂纹动态响应，对DSⅠFs以及荷载作用时间进行无量纲化处理，即：

式中：

C

为材料纵波波速，为7 337.85 m/s；

K

为量纲为一的应力强度因子；上标n 表示量纲为一；

K

(

t

)为动态应力强度因子。Ansys 求解结果与Lin 的计算结果如图3。由图3 可看出，两者所得的DSⅠFs 时程曲线非常吻合，验证了本文方法的可行性。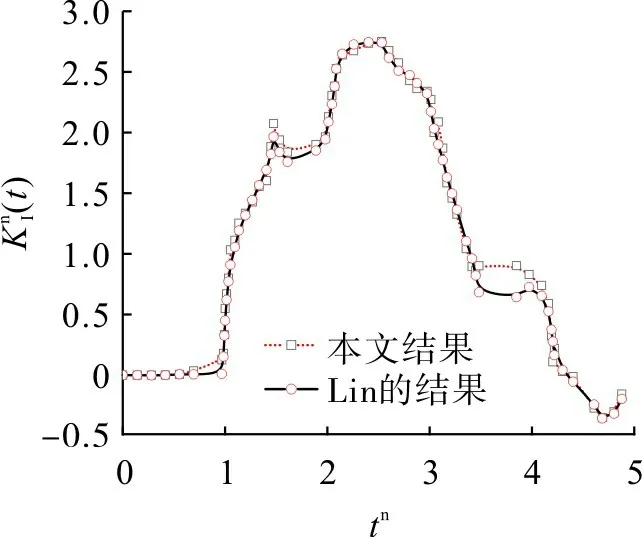

图3 本文结果与Lin结果的对比Fig.3 Comparison between the paperand Lin’s results

2 卸荷条件下动态应力强度因子计算模型

2.1 卸荷计算模型

卸荷条件下含单裂纹岩石计算模型如图4。模型边长

L

为10 cm，预设裂纹长度2

a

为4 cm，底部及模型左侧施加滑移支座约束。控制竖向荷载

σ

保持不变，侧向荷载

σ

逐渐卸荷至0，选取隆昌青砂岩为模拟材料：杨氏模量

E

= 17.67 GPa，泊松比

μ

=0.21，密度

ρ

= 3 055 kg/m，单轴抗压强度

σ

=67.8 MPa，静态断裂韧度

K

=0.658 MPa·m。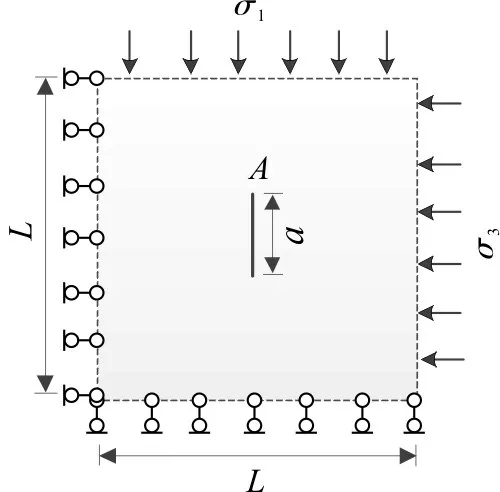

图4 含单条预设裂纹卸荷模型Fig.4 Unloading model with a single preset crack

有限元模型如图5（a）。模型共12 779 个节点，4 215 个单元，裂纹尖端具有奇异性，将裂纹尖端设置为1/4 奇异单元。整个卸荷模拟过程中轴压、围压变化都是通过编写的APDL 命令流进行控制的，其典型的轴压、围压变化过程如图5（b）。将

t

= 0 至

t

=

t

称为初始压力加载过程，

t

=

t

至

t

=

t

称为卸围压过程，

t

=

t

至

t

=

t

称为卸荷后持续过程。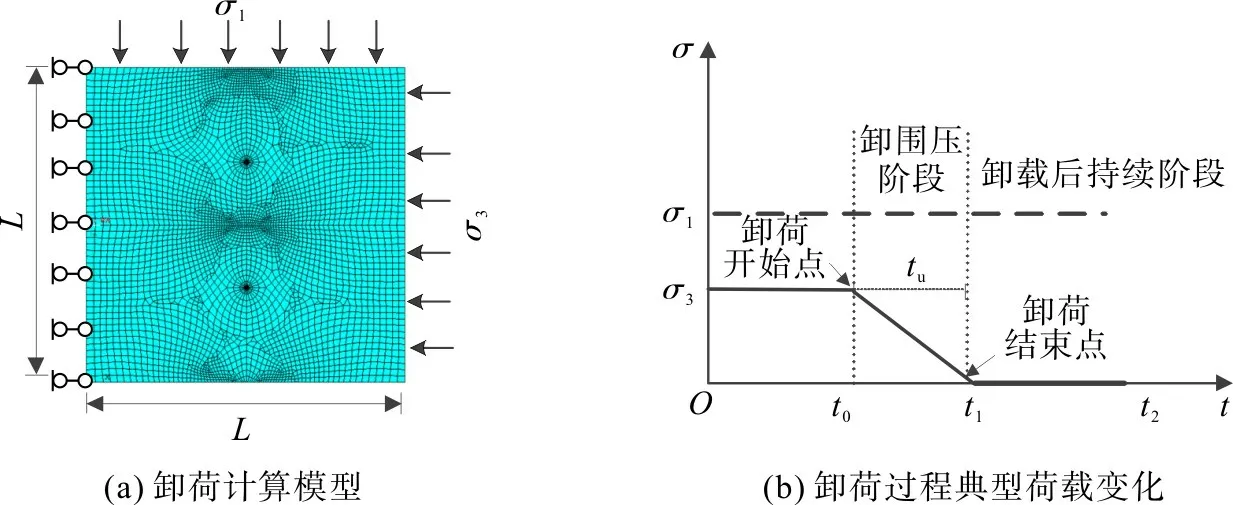

图5 卸荷计算模型和卸荷过程典型荷载变化Fig.5 Unloading colculation model and typical load variation in unload process

2.2 动态应力强度因子的计算

以

σ

=0.9

σ

，

σ

=0.7

σ

为例，参照Li 等利用PFC（particle flow code）进行开挖卸荷模拟使用的卸荷时间，设置卸荷时间

t

为200 μs，动态卸荷时间步长为0.1 μs，选取裂尖上端节点（

A

点）进行裂纹尖端DSⅠFs有限元计算，结果如图6。纵坐标

K

(

t

)为

式中：

K

(

t

)为动态应力强度因子；

K

为相同轴压下对应的Ⅰ型静态应力强度因子。通过式（10）可有效反映出卸荷引起的应力强度因子的动态效应。未添加、添加接触单元的

K

(

t

)时程曲线如图6，在接触面两侧的线单元设置目标单元和接触单元来建立接触对，界面摩擦系数为0.2、法向接触刚度系数

f

为1.0。由图6 可看出：未添加接触单元时，裂纹面在卸荷阶段由于受压应力作用，

K

(

t

)出现了较大负值，意味着在裂纹面处出现了较大程度的嵌入，这对计算精度有较大影响；添加接触单元后，DSⅠFs 基本不出现负值的情况，裂纹面发生嵌入的情况大大改善。

图6 添加接触单元的KIn (t)时程曲线Fig.6 Time history curves of KIn (t)with contact elements

3 动态应力强度因子影响因素分析

3.1 围压

取初始轴压

σ

= 0.9

σ

初始围压

σ

分别为0.7

σ

，0.5

σ

，0.4

σ

，0.2

σ

，卸荷时间200 μs，时间步长0.1 μs，计算取模型参数及卸荷路径如图5。求解此条件下裂纹尖端DSⅠFs 值，得到不同围压下DSⅠFs 时程曲线，结果如图7。从图7 可发现：随围压增加，DSⅠFs 曲线整体形状不变，峰值逐渐增加，且DSⅠFs 最大值均出现在卸荷时间250 μs 左右；围压越大，卸荷条件裂纹尖端的应力强度因子就越大，卸荷条件下的动态效应就越明显。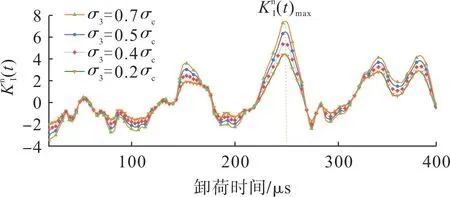

图7 不同围压下的KIn (t)时程曲线Fig.7 Time history curves of KIn (t)under different confining pressures

图8 为卸围压不同阶段数值模型对应的Von-Mises 应力云图。由图8 可看出：卸荷时间为53 μs 时，裂纹微量张开；卸荷时间为106 μs 时，裂纹闭合；卸荷时间为153 μs时，裂纹张开度出现明显增大。

K

(

t

)时程曲线在形态上表现为几个逐渐上升的波峰。由此可看出，在卸荷条件下裂纹面张开闭合发生震荡，致使应力强度因子发生震荡。

图8 卸荷过程中裂纹尖端Von-Mises应力云图Fig.8 Von-Mises equivalent stress contours during unloading process

3.2 轴压

取

σ

=0.3

σ

，0.6

σ

，0.9

σ

，控制围压

σ

=0.8

σ

不变，

σ

分别为0.2

σ

，0.5

σ

，0.7

σ

，围压卸荷时间为200 μs，动态卸荷时间步长为0.1 μs，模型计算参数及卸荷路径如图5。通过有限元求解裂尖应力场，得到不同轴压下的

K

(

t

)，结果如图9。图9表明，卸荷条件下不同轴压的

K

(

t

)曲线重合，表明卸荷速率相同时，轴压对卸荷下裂纹尖端DSⅠFs 的动态效应无影响。

图9 不同轴压下的 (t)时程曲线Fig.9 Time history curves of K (t)under different axial pressures

3.3 裂纹长度

为研究预设裂纹长度对卸荷条件下裂纹尖端应力场的影响，选取预设裂纹长度为3，4，6 cm，除裂纹长度外，模型计算参数及卸荷路径如图5，围压卸荷时间200 μs，动态卸荷时间步长0.1 μs，初始荷载

σ

= 0.9

σ

，

σ

= 0.7

σ

。不同裂纹长度下

K

(

t

)时程曲线如图10。由图10可得出：卸荷条件下裂纹长度越短，其动态效应越明显，表明动态效应随裂纹长度增加逐渐降低；从应变能角度分析，当岩石应变能密度相同时，裂纹长度越小，其受到卸荷扰动的效果就越明显。

图10 不同长度预设裂纹下的(t)时程曲线Fig.10 Time history curves of (t)of pre-exist cracks with different lengths

3.4 卸荷速率

在高应力条件下，围压卸荷结束，轴压持续作用一段时间，岩石才会发生岩爆，这点在相关数值模拟中也有所体现。表明卸围压对裂尖应力场产生的影响并不是只存在于卸围压过程中，卸荷一段时间内仍存在。取围压卸荷至0 的时间

t

为100，400，1 000 μs，3组卸荷时间表征高、中、低卸荷速率，取动态卸荷时间步长0.1 μs，将卸荷时间延长至卸荷后持续阶段（

t

时刻），取初始轴、围压

σ

= 0.9

σ

，

σ

= 0.7

σ

，模型计算参数及卸荷路径如图5，计算3 组卸荷速率下的

K

(

t

)时程曲线，结果如图11。由图11可得出：卸荷速率较快时(

t

=100,400 μs)，DSⅠFs最大值出现在卸荷后持续的一段时间，而不是在卸围压阶段，瞬态卸荷下DSⅠFs 最大值存在明显的滞后效应；卸荷速率较慢时(

t

=1000 μs)时，DSⅠFs最大值出现在卸围压阶段；卸荷速率越大，DSⅠFs对应的最大值

K

(

t

)越大，表明卸荷产生的动态效应越明显。

图11 不同卸荷速率下的（t）时程曲线Fig.11 Time history curves of （t）under different unloading rates

3.5 杨氏模量

为研究模型的杨氏模量对DSⅠFs 的影响，求解3组杨氏模量（

E

，2

E

，3

E

）下的裂尖DSⅠFs。取围压卸荷时间为200 μs、动态卸荷时间步长为0.1 μs，除材料杨氏模量外，模型计算参数及卸荷路径如图5，3 组杨氏模量对应的

K

（

t

）如图12。由图12 可得出：杨氏模量越大，

K

（

t

）时程曲线震荡频率越高，且DSⅠFs 峰值相较于小模量模型分布得越平均；杨氏模量越大，第一个波峰出现的时间越早，表明卸荷应力波越早到达裂纹尖端。

图12 不同杨氏模量下的(t)时程曲线Fig.12 Time history curves of (t)with different Young’s modulus

3.6 围岩刚度

岩爆体上下围岩的刚度与岩爆体不同，为研究围岩刚度对岩爆体动态裂纹扩展的影响，设置不同杨氏模量的围岩，其计算模型如图13。求出模量系数为

λ

= 0.5，1.0，2.0时，卸荷条件下不同硬度的围岩对裂纹尖端DSⅠFs的影响，结果如图14。

图13 软硬围岩计算模型Fig.13 Computational model of soft and hard surrounding rock

图14 不同刚度围岩对应的 (t)时程曲线Fig.14 Time history curves of (t)of surrounding rock with different stiffnesses

图中取围压卸荷时间为200 μs，动态卸荷时间步长为0.1 μs，初始荷载为

σ

= 0.9

σ

，

σ

= 0.7

σ

，模型计算参数及卸荷路径如图5，模型中仅改变围岩杨氏模量单一参数。由图14 可看出，相较于刚度较大围岩，围岩刚度较小时，裂纹尖端DSⅠFs增大明显，DSⅠFs峰值滞后出现。从应变能释放角度可对此现象进行解释，在加载阶段，相较于硬围岩，软岩可储存更多的应变能，围压卸荷时，储存在围岩中的应变能得到释放，DSⅠFs快速增长；相较于硬围岩，软岩释放能量较慢，表现为DSⅠFs峰值滞后出现。软围岩储能更多，卸荷条件下动态效应越强烈，越易诱发岩爆。对于抛掷型岩爆，单纯依靠岩爆体本身的能量是不够的，还需围岩补充供能。当围岩刚度较小时，岩石将储备更多的能量提供给岩爆体，进而发生岩爆。图14反映的规律与文献[17]的论述一致。

3.7 裂纹排布

为研究卸荷条件下，岩石中分布的平行裂纹对裂纹尖端应力场的影响，模拟平行等高（Case-b），平行非等高（Case-c）及平行非等长（Case-d，e）预制裂纹，如图15。试件边长为10 cm，设置初始荷载

σ

= 0.9

σ

，

σ

= 0.7

σ

，模型计算参数及卸荷路径如图5，选取含双条平行预制裂纹卸荷模型左侧上端节点为研究对象。侧裂纹上尖端DSⅠFs 曲线模拟结果如图16，17。由图16，17 可发现：当预设裂纹为等长等高（Case-b）时，DSⅠFs峰值减小，对于平行非等高裂纹（Case-c），

K

(

t

)曲线基本与对照组重合，峰值略有减小；对于不等长平行预制裂纹，当右侧裂纹较长时（Case-e），右侧裂纹对左侧裂纹尖端应力场影响最大，左侧裂纹尖端DSⅠFs峰值明显降低，当裂纹右侧较短时，对左侧裂纹尖端应力场影响较小，DSⅠFs峰值略微减小。由此可看出，双条平行预制裂纹之间的应力场相互影响，反映在DSⅠFs曲线上表现为峰值降低，且平行非等长裂纹对裂纹尖端应力场的影响最显著。

图15 含双条平行预制裂纹卸荷模型Fig.15 Unloading models with double parallel pre-exist cracks

图16 平行等长预制裂纹 (t)时程曲线Fig.16 Time history curves of (t)with parallel equal length pre-exist cracks

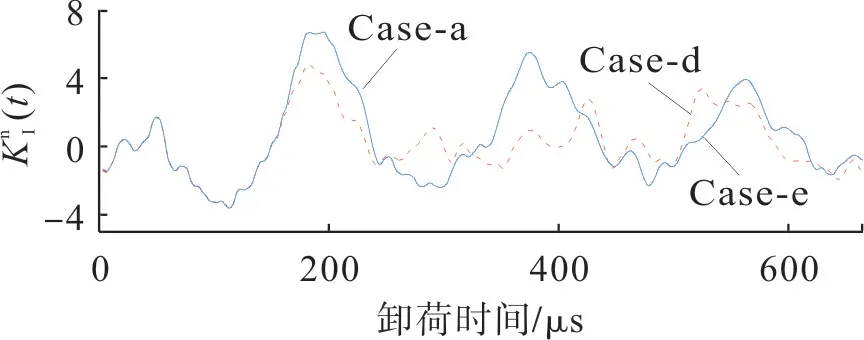
图17 平行等高预制裂纹 (t)时程曲线Fig.17 Time history curves of (t)with parallel equal height pre-exist crack

4 动态应力强度因子与动态断裂韧度增率分析

4.1 动态加载率-起裂韧度拟合曲线

综上分析可发现，卸荷速度越快，DSⅠFs 幅值越大，裂纹越易开裂。但根据文献[4]，DSⅠFs 增率越高，断裂韧度越大。说明卸荷速度快，DSⅠFs 增大不一定能引起裂纹扩展。为此，通过改变卸荷速率探究DSⅠFs 与动态断裂韧度增长速率的关系，既有动态加载率-起裂韧度关系实验结果可拟合为图18的形式，结果呈指数增长规律。

图18 动态加载率-起裂韧度拟合曲线Fig.18 Fitting curves of dynamic loading rate-initiation toughness

通过数据拟合得到两者之间关系如下：

式中：

K

(

t

)为材料的动态起裂韧度；

K

̇(

t

)为动态加载率；

R

为指数相关系数。

4.2 不同卸荷速率下的增长速率

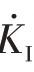
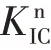
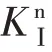
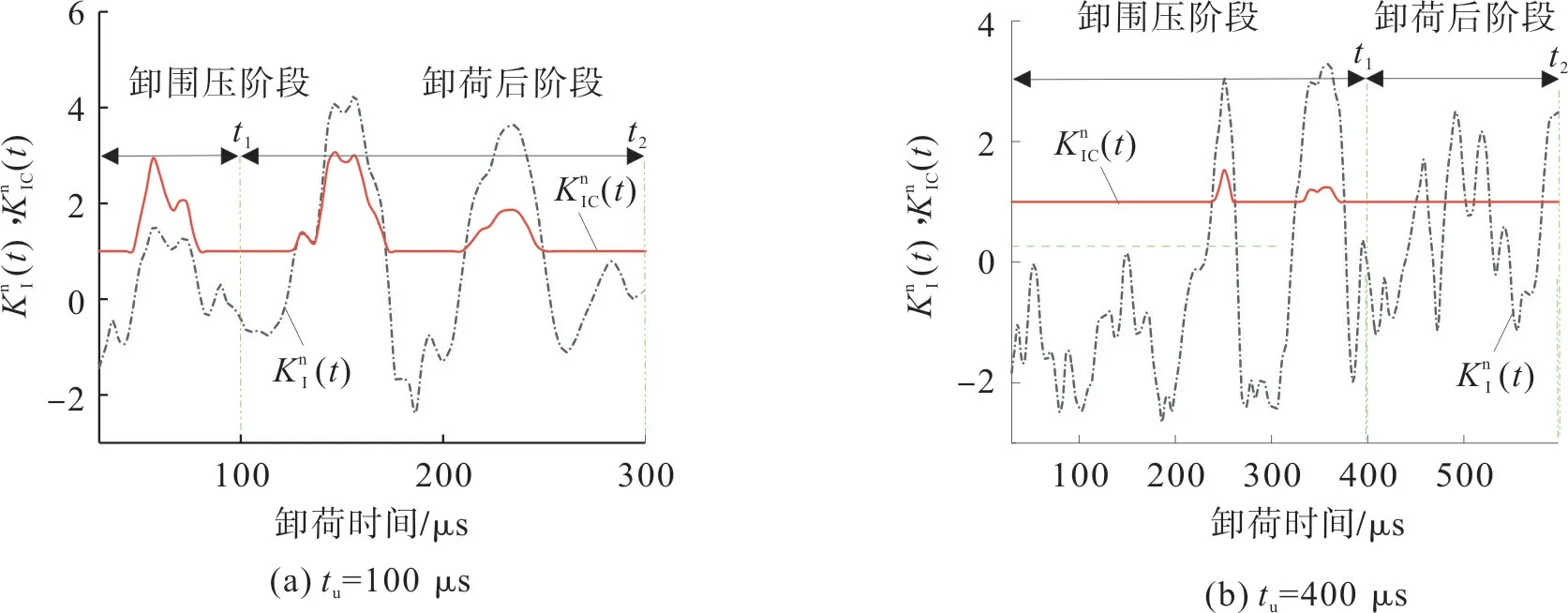
图19 不同卸荷速率下的(t)及(t)曲线Fig.19 K (t)and (t)curves under different unloading rate

图19表明：高卸荷速率下，卸围压初期起裂韧度增速大于DSⅠFs增速；随卸荷时间增加，DSⅠFs增速又逐渐大于起裂韧度增速，裂纹会在围压卸荷结束后的一段时间起裂；卸荷速率较慢时，裂纹起裂发生在卸围压过程中，且卸荷速率越大，起裂发生时间越短。

5 结论

利用数值模拟软件ANSYS对卸荷条件下的Ⅰ型DSⅠFs进行研究，得出如下主要结论：

1）卸荷条件下，围压和卸荷速率对裂纹尖端应力场产生影响，围压及卸荷速率越大，DSⅠFs峰值越大，卸荷产生的动态效应越明显；

2）围岩刚度越小，储存在岩石内部的应变能越大，卸荷条件下裂纹尖端DSⅠFs峰值越大，越易诱发岩爆；

3）瞬态卸荷时，DSⅠFs 最大值出现在卸荷后持续阶段，存在滞后效应，随应变能的释放，DSⅠFs 曲线出现明显衰减；

4）双条裂纹之间的应力场相互影响，反映在DSⅠFs曲线上为峰值降低，且平行非等长裂纹对降低卸荷条件下的动态效应最明显；

5）高卸荷速率下，卸围压初期，起裂韧度增速大于DSⅠFs增速，随卸荷时间增加，DSⅠFs增速逐渐大于起裂韧度增速，裂纹会在围压卸荷结束后的一段时间起裂。