基于改进蚁群算法的离散制造车间物料配送路径优化
陈 荣,卞东东,王雯阳
(安徽工业大学管理科学与工程学院,安徽马鞍山 243032)
离散型制造企业的生产模式正向着多品类、小批量、多批次的方向转变,同时越来越重视对生产余废料的回收作业,面临着考虑余废料回收的车间物料配送路径问题。余废料回收过程中,为有效减少车辆运行中的空载、降低作业成本、提高服务效率,一方面要保证自动引导车(automated guided vehicle,AGV)将物料及时准确高效地配送至工作站;另一方面要确保在AGV配送物料的过程中,根据实际载重回收工作站的余废料。对此,学者们对车间内物料配送作业的车辆路径问题(vehicle routing problem,VRP)进行了深入研究,如基于多种策略的VRP、考虑车间道路约束的VRP、考虑环保绿色的VRP及基于电子看板的VRP。
关于配送作业同时取送货的车辆路径问题(vehicle routing problem with simultaneous pick-up and delivery,VRPSPD)方面的研究有很多,如周蓉等针对多目标的VRPSPD,提出了一种基于节约法的自适应并行遗传算法;马艳芳等设计基于模糊随机算子的改进粒子群算法求解多目标的VRPSPD;Napoleao等研究了车辆异构的VRPSPD,设计带最邻近策略的快速随机算法对问题进行求解;Gong 等构建基于VRPSPD 的以制造商为主导的闭环供应链物流网络,设计两阶段多目标混合算法;盛虎宜等针对农村电商背景下的VRPSPD,以总配送成本最小构建共同配送策略;张晓楠等针对B2C 模式下的VRPSPD 设计改进遗传算法求解问题;李嘉等研究电动汽车的VRPSPD,构建以电动汽车固定使用成本和能耗成本之和最小的优化模型。分析以上文献可发现:对于车间内物料配送的VRP较少考虑车间余废料的回收,VRPSPD的研究对象是诸如农村电商、B2C的大环境,车间内的复杂小环境较少,且研究重点多为求解算法的创新;VRPSPD的优化目标多为路径成本、车辆固定使用成本等,较少考虑车辆的指派成本。鉴于此,提出带软曲线时间窗的物料配送及余废料回收一体化策略,构建考虑配送车辆、路径成本以及违背工位时间窗惩罚成本与总配送成本最小的优化模型,改进蚁群算法对离散车间内考虑回收的物料配送路径优化问题进行求解,实例结果表明了该算法的可行性和有效性。
1 问题描述及模型的构建
1.1 问题描述
离散制造车间内考虑余废料回收的物料配送路径优化问题可描述为:离散制造车间内有一个物料仓库和K
台自动引导车,N
个需要物料的工作站,若干个需要余废料处理的工作站,各工作站所需的物料及待回收的余废料数量均已知。物料仓库发出的车辆需在工作站的时间窗内进行物料的配送及余废料的回收服务,自动引导车在物料配送、余废料回收完成后回到物料仓库内。为便于模型构建,提出如下假设:1)所有AGV从物料仓库出发时,运载的物料量不能超过其最大运载量;
2)AGV 在对每个工作站服务时进行卸载物料的作业,若工作站有余废料回收的需求,则在卸载作业后进行装载作业,且装载的量与卸载后的负载量之和不能超过AGV的最大运载量;
3)AGV的唤醒、等待等时间忽略不计,卸、装载时间不同,行驶速度恒定,不考虑碰撞等情况;
4)所有AGV同时从物料仓库出发,完成任务后立即返回物料仓库;
5)每辆AGV可服务多个工作站,每个工作站只能由一辆小车服务;
6)AGV需在工作站规定的时间窗内提供服务,若违背时间窗会因工作站满意度降低而造成额外的惩罚成本;
7)物料以质量计算,对于货物的形状、体积等不考虑在内。
1.2 模型构建
1.2.1 模型参数
模型中相关参数变量及含义如表1。其中配送车辆违背时间窗造成的惩罚成本表达式如式(1)。

表1 参数变量Tab.1 Parameter variable scale
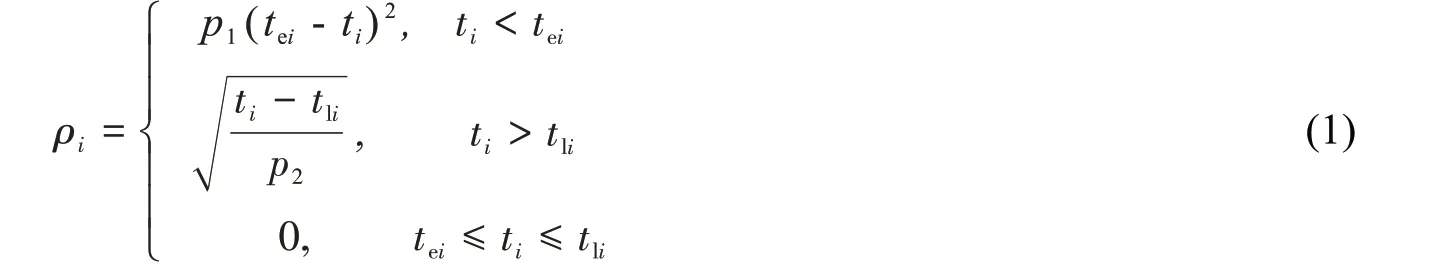
传统直线软时间窗并不适用于离散制造车间复杂的环境,而曲线软时间窗更贴近实际离散制造车间物料配送路径优化问题:配送车辆提前到达的时间越长,其单位时间的惩罚成本应越大,如需求点没有足够的空间存储早到的物料;延迟到达的时间越长,其单位时间的惩罚成本应越低,如在等待的过程中可使用替代方案弥补。
1.2.2 数学模型
针对离散车间内考虑余废料回收的物料配送路径优化问题,建立考虑配送车辆、路径长度及违背时间窗惩罚成本的总配送成本最小的路径优化模型。
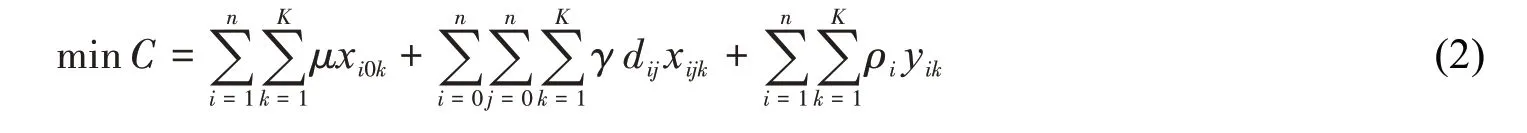
s.t.

μ
为单位车辆的指派成本;γ
为单位距离的路径成本;M
为一个数值极大的正数。目标函数式(2)包括三部分,即指派车辆成本最少、配送距离最短以及惩罚成本最低,通过成本的方式转化为配送总成本,将多目标合并为单目标,并以该单目标建立路径优化模型。式(3)表示每个工作站只被服务1 次且仅有1 辆小车执行任务;式(4)确保指派的车辆数小于总车辆数;式(5)构成回路,即车辆到达的工作站数等于离开的工作站数;式(6)表示每辆车离开工作站i
、服务工作站j
时,确保车上载质量不超过车的最大容量;式(7),(8)分别表示每辆车在服务所有工作站时的物料配送量、余废料回收量都不大于车辆的最大容量;式(9)为车辆k
从工作站i
到工作站j
所要满足的时间条件。2 蚁群算法的改进
蚁群算法由Dorigo 等提出,其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。蚁群算法是一种用来寻求最优路径的概率型算法,本质上是进化算法中的一种启发式全局优化算法,具有分布计算、信息正反馈和启发式搜索等特征。但蚁群算法存在收敛速度慢、容易陷入局部最优等不足。对此文中提出随机性与确定性相结合的路径搜索策略,并将二元素优化算法、遗传算法嵌入蚂蚁寻优的过程中,以改善蚁群算法的性能。改进蚁群算法的步骤如下:
1)初始化参数,设定每条路径的初始信息素浓度τ
( )0 ,将若干蚂蚁放置在物料仓库,同时建立禁忌表。2)蚂蚁k
对未经访问的下一节点j
进行选择,节点的选择由式(10)确定。
α
为信息启发式因子;β
为期望启发式因子;η
为蚂蚁从节点i
移至节点j
的可见度;q
为蚂蚁在执行随机性与确定性相结合的路径搜索策略时设置的值,其会随着算法迭代的过程发生变化,通过与随机数q
比较以控制蚂蚁确定下一路径搜索的方式。当蚂蚁k
对未经访问的下一节点j
时,随机产生q
∈[0,1],若q
<q
,则蚂蚁按照已知路径中最大概率选择下一个节点,为确定性搜索;若q
≥q
,则蚂蚁根据基本蚁群算法中的概率进行选择,为随机性搜索。在蚂蚁寻优早期,将q
设置为一个较大值,使蚂蚁按照确定性搜索选择下一路径,达到更快找到相对优解的目的;在蚂蚁寻优中期,为跳出局部最优,扩大蚂蚁搜索的范围,将q
设置为一个较小值,使蚂蚁按照随机性搜索选择下一路径;在蚂蚁寻优后期,恢复q
的值再次加快算法的收敛速度;若q
<q
,则执行步骤3),否则执行步骤4)。
k
根据式(11)选择下一节点j
。5)判断蚂蚁k
到达节点j
后是否满足约束条件,若满足则将该节点放入禁忌表,若不满足则返回步骤2)。6)将蚂蚁移动产生的路径进行2-opt优化,保存其产生的最优解。
7)判断蚂蚁是否经过所有节点,若已达成则将全局最优解和部分次优解作为初始种群进行交叉、变异等遗传操作,否则转回步骤2)。
8)比较遗传算法得到的新解和原有解,若更优秀则替代原有解,否则保留。
9)对每一只蚂蚁经过的路径进行信息素和信息增量更新,当蚂蚁从节点i
按照转移策略转移到节点j
时,在节点i
与j
之间的路径上被蚂蚁留下的信息素更新为τ
(t
+ 1) =(1-ρ
)τ
(t
) +Δτ
(t
),其中:
ρ
为信息素挥发因子;1-ρ
为信息素残留因子;τ
(t
)为未更新的路径的(i
,j
)信息素量;Δτ
(t
)为所有蚂蚁在路径(i
,j
)上留下的信息素量;L
为全局最优解。10)判断是否到达最大迭代次数,若是则停止迭代,输出最优解;否则,清空禁忌表,转回步骤2)。
3 实例验证
3.1 数据设定
离散车间有1个物料仓库和20个工作站,可派遣车辆为6辆,将该车间一天的工作时间分为4个周期,在每个周期末会进行余废料的回收作业。设置参数如下:最大迭代次数为200 次,种群规模为30 只,信息启发式因子为4,期望启发式因子为1.25,信息素挥发因子为0.30,信息素增加量为50,迭代前期及后期q
为0.80、中期q
为0.20;AGV 的指派成本为15 元/辆,最大载质量为100 kg,单位运输成本为1.50 元/m,运行速度为1 m/s;提前将物料送至工作站的惩罚成本系数p
= 30,延迟到达工作站的惩罚成本系数p
= 20。物料仓库和各工作站基本信息如表2,物料仓库、工作站之间的运输时间如表3。
表2 工作站基本信息Tab.2 Basic information for workstations
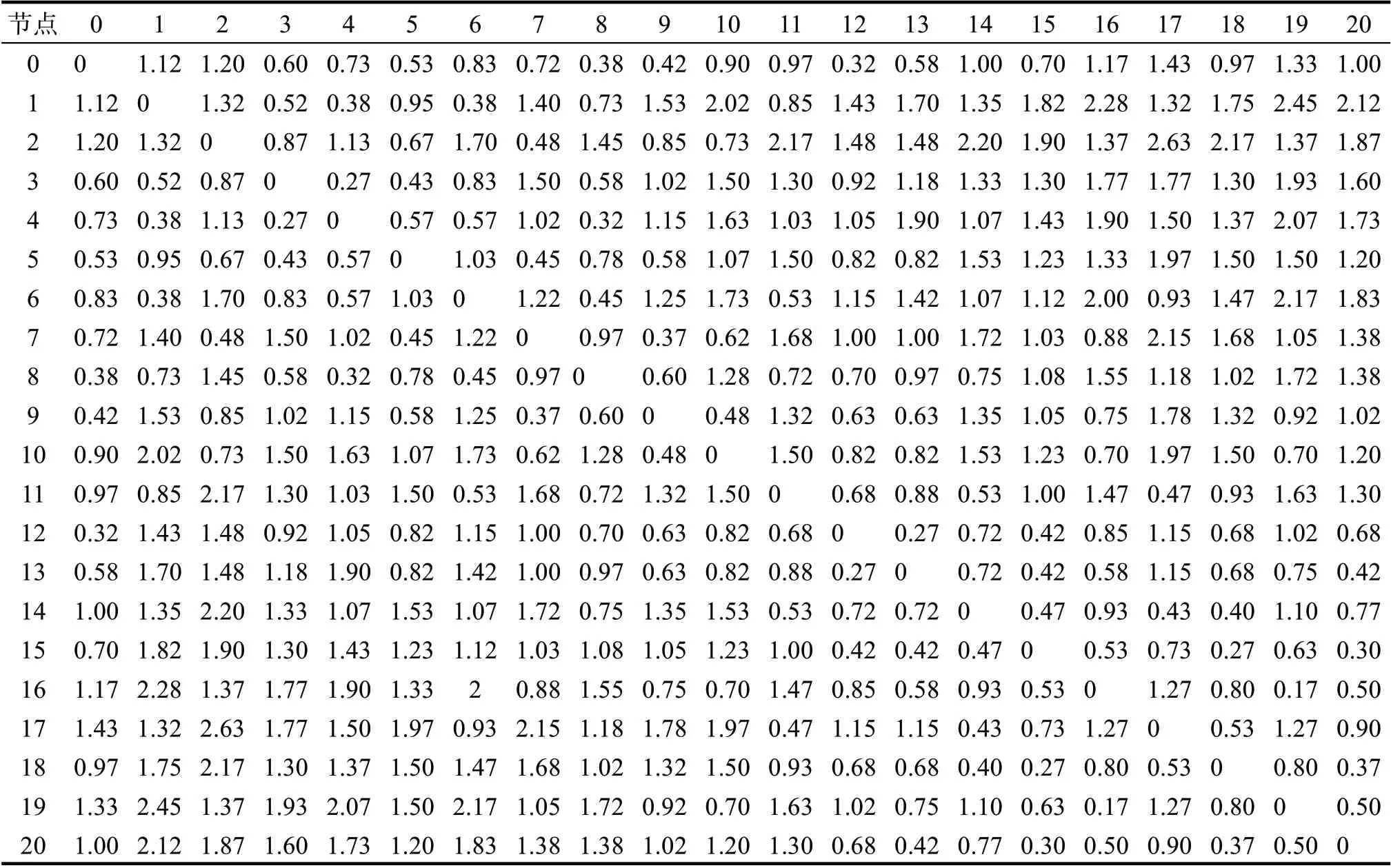
表3 车间内各节点间标准配送时间单位:minTab.3 Standard distribution schedule between nodes in the workshopUnit:min
3.2 实例结果及分析
针对该实例,使用MATLABR2017a 软件,采用基本蚁群算法和改进的蚁群算法对以总配送成本最小为目标的离散车间内考虑余废料回收的物料配送路径优化问题进行求解,求解结果如图1。

图1 迭代结果Fig.1 Iterative result
分析图1 可发现:基本蚁群算法在初始解以及最终解都没有改进蚁群算法优秀;基础蚁群算法在迭代到30 次左右就几乎收敛,陷入局部最优;改进的蚁群算法在算法迭代前期,快速找到一个相对较优的解,迭代中期跳出局部最优,扩大了蚂蚁搜索的范围,迭代后期加速收敛。采用基本蚁群算法解决离散车间内考虑余废料回收的物料配送路径优化问题的结果如表4。由表4可看出:物料仓库分别派遣4辆车对20 个工作站进行物料配送及余废料回收,路线1 为0-14-45-7-0、路线2 为0-6-1-19-16-12-8-0、路线3 为0-9-10-20-13-17-11-0、路线4 为0-3-18-15-2-0;路径成本1 578 元,降低满意度而产生的惩罚成本为37元,车辆平均负载率70%。

表4 基本蚁群算法结果Tab.4 Results of the basic ant colony algorithm
采用改进的蚁群算法求解离散车间内考虑余废料回收的物料配送路径优化问题,结果如表5。由表5可看出:物料仓库分别派遣3辆车对20个工作站进行物料配送及余废料回收,路线1为0-11-17-14-8-4-1-3-0、路线2 为0-7-16-19-15-20-10-9-0、路线3 为0-12-18-13-5-2-6-0;路径成本1 275 元,降低满意度而产生的惩罚成本为25元,车辆平均负载率93%。

表5 改进蚁群算法结果Tab.5 Results of the improved ant colony algorithm
采用基本蚁群算法与改进的蚁群算法解决离散车间内考虑余废料回收的物料配送路径优化问题,结果如表6。由表6可看出:在派遣配送与回收的车辆数量与车辆派遣成本上,后者相对于前者优化了25%;在损害满意度而产生的成本上,后者相对于前者优化了32%;在配送总距离与配送及回收路径成本上,后者相对于前者优化了19%;在平均负载率上,后者相对于前者优化了33%;在配送总成本上,后者相对于前者优化了20%。以上分析表明:相比于基本蚁群算法,改进的蚁群算法在路径成本、惩罚成本及指派车辆数量上都有显著的优化,验证了算法的可行性与有效性。

表6 路径优化结果对比Tab.6 Comparison of results of route optimization
4 结论
针对离散制造车间内物料配送不及时、配送车辆负载率低、路径成本高等问题,提出带软曲线时间窗的物料配送及余废料回收一体化策略,建立以总配送成本最少为目标的路径优化模型,改进蚁群算法对离散车间内考虑余废料回收的物料配送路径优化问题进行求解,最后通过实例验证。结果表明:相比于基本蚁群算法,采用改进的蚁群算法在该问题上配送总成本优化了20%,配送AGV 减少1辆,小车来回程的负载率提升了33%,提高了物料配送及余废料回收的及时性和准确性,采用改进的蚁群算法对离散车间内考虑回收的物料配送路径问题优化效果明显,具有较强的实用性。

