幂零元的单边零可交换性
何 萍,赵 良
(安徽工业大学数理科学与工程学院,安徽马鞍山 243032)
文中R
表示有单位元的环,N
(R
)表示环R
中所有幂零元的集合,M
(R
)表示R
上的n
×n
全矩阵环,U
(R
)表示R
上的n
×n
上三角矩阵环,D
(R
)表示主对角线元素相等的所有矩阵环。对任意a
∈R
,a
在R
中的右零化子记为r
(a
) = {b
∈R
|ab
= 0},a
在R
中的左零化子记为l
(a
) = {b
∈R
|ba
= 0}。称环R
是约化环,如果对所有的a
∈R
,由a
= 0 可推出a
= 0。根据文献[1],称环R
为可逆环,如果对所有a
,b
∈R
,由ab
= 0 可推出ba
= 0,显然每一个约化环是可逆环。Anderson 等研究了环的零交换性质,并用ZC
表示可逆环。如果对所有的a
,b
∈R
,由ab
= 0 可得到aRb
= 0,则称这样的环为半交换环,每一个可逆环都是半交换环。进一步地,Baser 等研究了相对于环的自同态的半交换性质和可逆性质,Zhao 等还研究了幺半群环上的可逆性质。对于可逆环和半交换环的幂零结构的研究,是近年非交换环论的一个研究热点。根据文献[6],环R
称为CNZ 环,如果对任意a
,b
∈N
(R
),由ab
= 0 可推出ba
= 0。进一步地,Mohammadi 等研究了诣零半交换环,称环R
为诣零半交换环,如果对任意a
,b
∈N
(R
),由ab
= 0 可推出aRb
= 0。显然,CNZ 环和诣零半交换环是两类性质完全不同的环,但它们从不同方面分别揭示了幂零元的交换性质。关于可逆环及其相关环的幂零结构的研究,可参考文献[8-10]。由此,有如下问题:若CNZ环中只有一个元素是幂零元,这样的环又具有怎样的幂零结构?受上述研究启发,进一步研究幂零元的单边零交换性质,即在CNZ 环中当有一个元素是幂零元时的两个元素的零交换性质,将具有这种性质的环称为左幂零可逆环和右幂零可逆环;通过构造反例说明左(或右)幂零可逆环是CNZ环的一个真子类,并给出可逆环和左(或右)幂零可逆环等价的条件。1 左幂零可逆环
引入左幂零可逆环和右幂零可逆环的概念,并给出相关的例子。
定义1
称R
为左幂零可逆环,如果对任意a
∈N
(R
),b
∈R
,由ab
= 0 可推出ba
= 0。类似地,称环R
是右零可逆环,如果对任意a
∈R
,b
∈N
(R
),由ab
= 0可推出ba
= 0。由定义1可知,每一个可逆环都是左幂零可逆环和右幂零可逆环,且每一个左幂零可逆环和右幂零可逆环都是CNZ环。
引理1
左幂零可逆环关于子环、直和和直积是封闭的。例1
设K
是域,令R
=M
(K
)。则R
的幂零元只有3种形式,分别为:
例1表明,CNZ环不一定是左(或右)幂零可逆的,从而左右幂零可逆环是CNZ环的一个真子类。
命题1给出了左幂零可逆环和可逆环等价的条件。
命题1
设R
是半素环,则以下条件等价:1)R
是约化环;2)R
是对称环;3)R
是可逆环;4)R
是左幂零可逆环。命题1的证明
1) ⇒2) ⇒3) ⇒4)由定义显然,只需证明4) ⇒1)。如果a
∈R
且满足条件a
= 0,那么a
∈N
(R
)。对任意r
∈R
,有a
r
=a
(ar
) = 0。因为R
是左幂零可逆环,所以aRa
= 0,再由R
是半素环可得a
= 0。推论1
环R
是可逆的当且仅当R
是半素的左幂零可逆环。命题2给出了如何利用矩阵扩张得到更多左(或右)幂零可逆环。
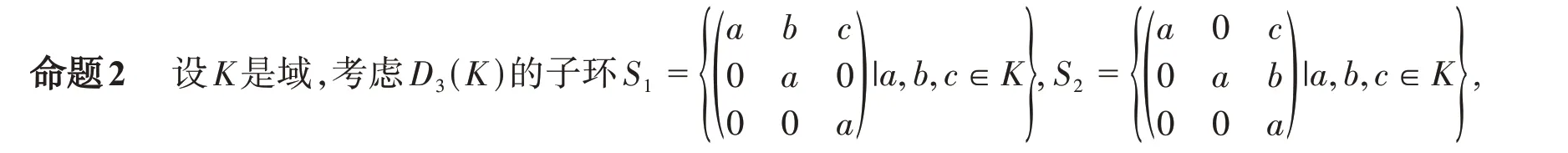
S
和S
都是左右幂零可逆环。命题2的证明
先证明S
是左右幂零可逆环,类似地,可证明S
是左右幂零可逆环。设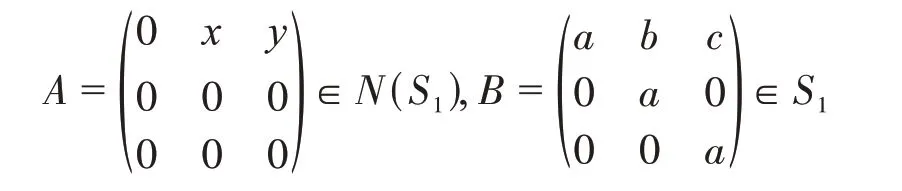
则

xa
= 0,ya
= 0,由此可得ax
= 0,ay
= 0。因此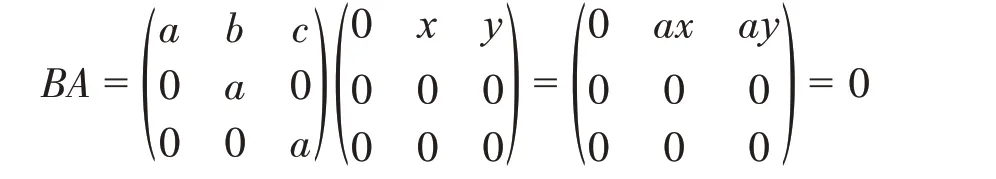
S
是左幂零可逆环,类似地,可证明S
是右幂零可逆环。命题3利用幂零元的零化子,对左幂零可逆环和右幂零可逆环给出了等价刻画。
命题3
设a
是R
的幂零元素,则:R
是左幂零可逆环当且仅当r
(a
) ⊆l
(a
);R
是右幂零可逆环当且仅当l
(a
) ⊆r(a
)。命题3的证明
假设R
是左幂零可逆环,且b
∈r
(a
),那么ab
= 0。因为a
是R
的幂零元素,R
是左零可逆环,所以有ba
= 0。于是,b
∈l
(a
),从而r
(a
) ⊆l
(a
)。反之,若r
(a
) ⊆l
(a
)且对a
∈N
(R
),b
∈R
有ab
= 0,则b
∈r
(a
)。由r
(a
) ⊆l
(a
)可得b
∈l
(a
),
即ba
= 0。因此,R
是左幂零可逆环。类似地,可证明R
是右幂零可逆环当且仅当l
(a
) ⊆r
(a
)。命题4
设R
是一个环且e
是R
的中心幂等元,则R
是左幂零可逆环当且仅当eR
和()1-e R
都是左幂零可逆环。命题4的证明
因R
≌eR
⊕(1-e
)R
,由引理1可直接得到。命题5
设R
/I
为左幂零可逆环,若I
是R
的一个约化理想(作为一个没有单位元的环),则R
是左幂零可逆环。
命题6 的证明
设a
,b
∈N
(R
)使ab
= 0。因为R
是左幂零可逆环,有ba
= 0。对于任意r
∈R
都有bar
= 0,由R
是左幂零可逆的可得arb
= 0,故R
是诣零半交换环。更一般地,命题7说明可通过约化环的平凡扩张得到更多的左幂零可逆环。
命题7
设R
是约化环,则T
(R
,R
)是左幂零可逆环。
命题8
设R
是一个环,α
为R
的单自同态,则R
是左幂零可逆环当且仅当A
(R
,α
)是左幂零可逆环。
2 左幂零可逆环的扩张
设R
是交换环S
上的代数,则R
关于S
的Dorroh扩张是Abelian群D
=R
⊕S
,其加法和乘法运算分别为:
r
∈R
,s
∈S
。定理1
设R
是交换环S
上的代数,如果S
是整环且R
是左幂零可逆环,那么R
关于S
的Dorroh 扩张D
是左幂零可逆环。定理1 的证明
假设R
是左幂零可逆环,则N
(D
) = {(r,
0)|r
∈N
(R
)}。设(r
,
0),(r
,s
)∈D
满足(r
,
0)(r
,s
) = 0,则有r
r
+s
r
= 0。因为R
是左幂零可逆环且S
为交换整环,所以有r
r
+s
r
= 0。于是可得(r
,s
)(r
,0) =(r
r
+s
r
,0) = 0,这就证明了R
关于S
的Dorroh扩张D
为左幂零可逆的。设R
为交换环,则通过R
的自同构σ
和模M
可定义R
关于模M
的斜平凡扩张R
⊕M
,其加法为普通加法运算,乘法运算为(r
,m
)(r
,m
) =(r
r
,σ
(r
)m
+r
m
),其中r
∈R
,m
∈M
。特别地,如果σ ≡I
,那么R
的斜平凡扩展就是R
的平凡扩张,并且用T
(R
,M
)表示。命题9
设R
为交换整环且σ
是R
的单自同态,则R
关于R
和σ
的斜平凡扩张是左幂零可逆环。命题9的证明
因为R
是交换整环,所以有N
()R
⊕R
= {(0,r
)|r
∈R
}。假设(0,m
)∈N
()R
⊕R
,(r
,m
)∈R
⊕R
使(0,m
)(r
,m
) = 0,那么r
m
= 0。因为R
是一个整环,所以r
= 0 或m
= 0。又因σ
是R
的单自同态,在这两种情况下都可得到σ
(r
)m
= 0,故(r
,m
)(0,m
) =(0,σ
(r
)m
)= 0。设a
,b
∈R
且b
为正则元,若存在a
,b
∈R
使ab
=ba
,则环R
称为右Ore环。一个环R
是右Ore环当且仅当R
存在经典右商环Q
。命题10
设R
是一个右Ore环,Q
是R
的经典右商环。如果R
是左幂零可逆的,那么Q
是左幂零可逆的。
R
是环,用R
[x
]表示R
关于未定元x
的多项式环,Δ
是由R
的中心正则元素作成的乘法幺半群。令Δ
R
={u
a
|u
∈Δ
,a
∈R
} ,则Δ
R
是一个环。命题11
设R
是一个环。则有如下论断:R
是左幂零可逆的当且仅当Δ
R
是左幂零可逆的;R
[x
]是左幂零可逆当且仅当Δ
R
[x
]是左幂零可逆的。命题11 的证明
由引理1,只需证明必要性。设α =u
a
∈N
(Δ
R
),β
=v
b
∈Δ
R
。如果αβ
= 0,a
∈N
(R
),b
∈R
,那么0 =αβ
=u
av
b
= (u
v
)ab
= (uv
)ab
,于是可得ab
= 0。因为R
是左幂零可逆环,所以ba
= 0。由此可推出βα
=v
bu
a
= (v
u
)ba
= 0,这就证明了Δ
R
是左幂零可逆环。
推论2
对于环R
,R
[x
]是左幂零可逆当且仅当R
[x
;x
]是左幂零可逆的。根据文献[12],如果对多项式f
(x
) =a
+a
x
+ …+ax
,g
(x
) =b
+b
x
+ …+bx
∈R
[ ]x
, 由f
(x
)g
(x
) = 0 可推出ab
= 0,则称环R
是Armendariz环。下面的命题给出了如何利用多项式扩张得到更多的左幂零可逆环。命题12
设R
是Armendariz 环,则以下各条等价:1)R
是左幂零可逆环;2)R
[x
]是左幂零可逆环;3)R
[x
;x
]是左幂零可逆环。命题12的证明
由引理1 和推论2,只需证明命题12 中1)⇒2)。设f
(x
)=a
+a
x
+…+ax
∈N
(R
[x
]),g
(x
)=b
+b
x
+ …+bx
∈R
[x
]满足f
(x
)g
(x
)=0。因为R
是Armendariz环,所以ab
= 0。由文献[13]中引理5.2可知,f
(x
)的每一个系数a
都是R
的幂零元。又因为R
是左幂零可逆的,所以ba
= 0,说明g
(x
)f
(x
) = 0,故R
[x
]是左幂零可逆的。文献[14]中将多项式环的Armendariz 性质进一步扩展到幂级数环R
[[x
]],这里R
[[x
]]表示环上关于未定元x
的幂级数环。称环R
为幂级数Armendariz 环,如果对任意f
(x
),g
(x
) ∈R
[[x
]],由f
(x
)g
(x
) = 0 可推出ab
= 0,其中a
∈C
,b
∈C
。根据文献[14]例2.1,每一个幂级数Armendariz 环都是Armendariz 环,但反之不成立。推论3
设R
是幂级数Armendariz环,则以下条件等价:1)R
是左幂零可逆环;2)R
[x
]是左幂零可逆环;3)R
[[x
]]是左幂零可逆环。推论3 的证明
因为每一个幂级数Armendariz 环都是Armendariz 环,由引理1 和命题12 知只需证明1)⇒3)成立。事实上,若R
是幂级数Armendariz 环,则由文献[14]中引理2.3(2)和文献[15]中引理2 可知N
(R
[[x
]]) ⊆N
(R
)[[x
]]成立。于是,类似于命题12的证明,可证明R
[[x
]]是左幂零可逆环。
