基于正六边形栅格JPS算法的智能体路径规划
王文明, 杜佳璐
(1. 大连海事大学轮机工程学院, 辽宁 大连 116026;2. 大连海事大学船舶电气工程学院, 辽宁 大连 116026)
0 引 言
随着现代科技的飞速发展,无人车、无人机、无人船等智能体应运而生,并被广泛应用于各个领域。智能体的路径规划技术是实现其自主导航的关键技术之一,也是智能化水平的体现。智能体的路径规划旨在根据当前的任务需求,规划出一条从起始点至目标点无碰撞、安全合理的路径[1],其核心是路径规划算法的设计。从传统算法到各种算法的组合优化,再到结合仿生学发展起来的智能优化算法[2],路径规划算法已经取得了巨大的进步。不同的路径规划算法有着其各自适用的范围和领域,传统的全局路径规划方法有Dijkstra算法[3]、A*算法[4]、跳点搜索(jump point search,JPS)算法[5]、人工势场法[6]等。其中,JPS算法是Daniel Harabor和Alban Grastien于2011年提出的正方形栅格地图下的路径规划算法。该方法优化了A*算法寻找后继节点的操作,提高了路径规划效率[7],因此被广泛应用于智能体的全局路径规划[8-13]。
2016年邱磊[14]等利用JPS算法解决移动机器人的路径规划问题,并在障碍物分布情况不同的3张地图上进行仿真验证,进而与A*算法进行仿真比较,结果表明,在保证路径最短的前提下,JPS算法的路径规划效率比A*算法高。2019年Ma[15]等利用JPS算法解决了机器人在家庭服务过程中的室内路径规划问题,仿真结果也表明JPS算法比A*算法路径规划效率高。2020年武达[16]等利用JPS算法解决矿用机器人在矿井巷道内的避障路径规划问题,仿真实验结果表明JPS算法的路径规划速度较传统A*算法提高了约2倍。然而,传统正方形栅格JPS(后文简称传统JPS)算法规划出的路径存在穿越墙角的不安全行为,智能体跟踪该路径移动易与障碍物发生碰撞。近年来有研究者以正六边形代替正方形对环境地图进行栅格化建模,并在正六边形栅格地图的基础上结合蚁群算法[17-18]、A*算法[19-20]等解决智能体的路径规划问题,结果表明与基于正方形栅格地图所规划的路径相比,基于正六边形栅格地图所规划的路径可以避免穿越墙角的行为,与障碍物的距离更安全合理。
受上述文献启发,利用正六边形栅格地图解决传统JPS算法规划所得路径存在穿越墙角的不安全行为。但在正六边形栅格地图上应用传统JPS算法存在搜索方向不确定、强制邻居判断规则、跳点搜索策略不适用等问题,为此本文修改传统JPS算法的邻居剪枝、强制邻居判断的规则和跳点搜索策略,提出一种新的正六边形栅格JPS(后文简称HJPS)算法,提高了智能体路径规划的质量和效率。
1 HJPS算法的正六边形栅格地图建模
图1所示的六边形称为顶角型正六边形。
图1 顶角型正六边形Fig.1 Vertex type regular hexagon
如图2所示,在二维平面环境中有一长为L、宽为W的矩形区域,其内部分布着有限个静态障碍物。为便于研究并保证利用HJPS算法进行路径规划的合理性,做出以下假设:
假设 1智能体在直径为a的圆形范围内;
假设 2智能体的移动指从所在栅格中心点移动至邻居栅格的中心点;
假设 3在智能体移动过程中,周围环境保持不变。
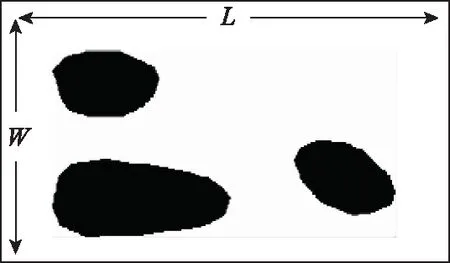
图2 矩形区域地图Fig.2 Rectangular area map
在上述条件下构建正六边形栅格地图,如图3所示,设定矩形区域的左上角为原点O,建立直角坐标系O-XY,规定水平向右为X轴正方向,竖直向下为Y轴正方向,采用边长为a相同大小的顶角型正六边形栅格铺满矩形区域,考虑假设1和假设2,智能体在该正六边形栅格地图中可被视作质点。进而根据矩形区域的实际环境情况将栅格标记为白色和黑色栅格,智能体可自由通过的栅格被标记成白色栅格,称为自由栅格;部分或全部由障碍物占据的栅格被标记成黑色栅格,称为障碍物栅格,智能体不能通过该栅格。

图3 矩形区域的正六边形栅格地图Fig.3 Regular hexagon grid map of rectangular area
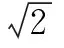
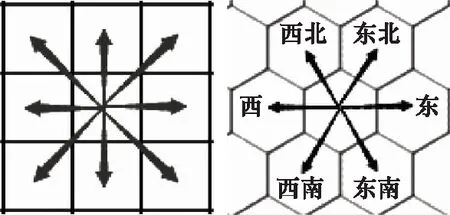
图4 智能体的移动方向Fig.4 Moving directions of agent
图5为智能体在不同栅格地图中的避障移动方式示意图,由图5可见,对比智能体在正方形栅格地图中的避障移动方式,智能体在正六边形栅格地图中的避障移动方式可避免穿越墙角的不安全行为,因此避障过程更安全合理。
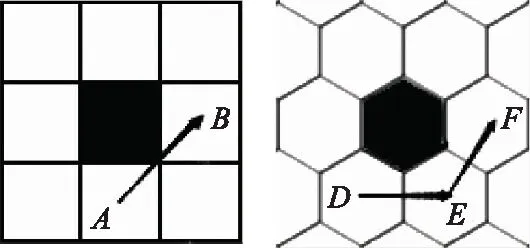
图5 智能体避障移动方式示意图Fig.5 Schematic diagram of obstacle avoidance moving ways of agent
2 HJPS算法
在A*算法的框架基础上,传统JPS算法通过邻居剪枝、强制邻居判断的规则和JPS策略搜寻后继节点[22],如图6所示,xp为节点x的父节点,J为跳点,N为强制邻居。若要在xp指向x的方向上寻找后继节点,邻居剪枝是剪枝掉图中灰色栅格所代表的邻居节点;强制邻居是在当前搜索方向周围存在障碍物时必须被考虑的邻居节点,如节点N;JPS策略是如何搜索到伴有强制邻居的跳点。上述过程可确定跳点J为xp指向x方向上的后继节点。
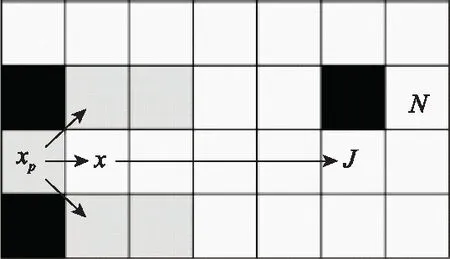
图6 东方向上寻找后继节点示意图Fig.6 Schematic diagram of finding the successor node in the east direction
在正六边形栅格地图上,智能体的移动方向由正方形栅格地图情况下的8个变为6个,跳点搜索方向随之变化,导致传统JPS算法的邻居剪枝和强制邻居判断的规则均不再适用,因此需要针对正六边形栅格地图的具体情况修改邻居剪枝和强制邻居判断的规则,并制定新的跳点搜索策略,以在正六边形栅格地图中实现JPS算法,即HJPS算法。
2.1 三斜轴坐标系
三斜轴坐标系O-xyz如图7所示,坐标原点为O,Ox、Oy和Oz轴与水平方向的夹角分别为30°、150°和270°[20]。若正六边形的边长为a,则设坐标轴的单位长度s=1.5a,从某节点d1分别向Ox、Oy、Oz轴作垂线,交于a、b、c三点,则d1的坐标为
(1)
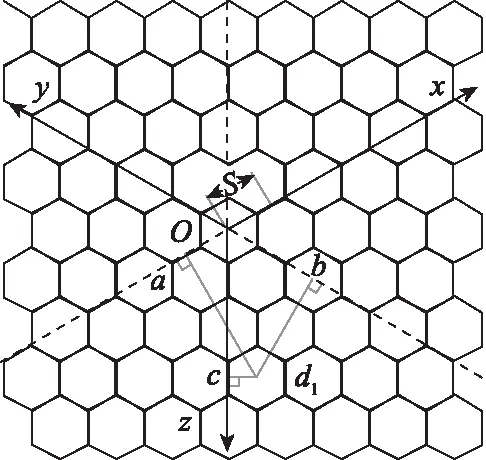
图7 正六边形三斜轴坐标系Fig.7 Regular hexagon coordinate system with three inclined axes
利用直角坐标系构建正六边形栅格地图便于障碍物信息的存储,但在直角坐标系中,当某栅格节点位于奇数行或偶数行时,其6个邻居节点的坐标需要通过不同的坐标关系进行计算;而在三斜轴坐标系中,已知任一正六边形栅格节点的坐标,其6个邻居节点的坐标可通过固定的坐标关系进行计算[23],这可以提高HJPS算法的运行效率。因此,选用直角坐标系构建正六边形栅格地图,并存储地图信息,选用三斜轴坐标系实现HJPS算法。
2.2 HJPS算法的邻居剪枝和强制邻居判断规则
设栅格地图中的某一连续节点序列H={x0,x1,…,xk},H中的各个节点xi所在的栅格是顺次逐个相邻的。设栅格地图中某一节点x的邻居节点为ni(i=1, 2,…, 6),节点x的父节点为xp,xp指向节点x的方向为剪枝方向,Hx表示节点x不在H中,len(H)表示H的节点个数。
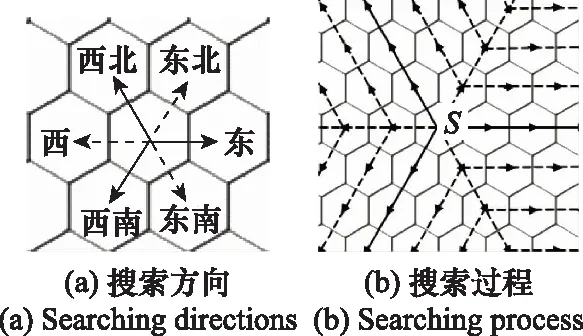
在正方形栅格地图中,东、西、南、北4个方向与所在正方形栅格的边垂直,称为垂直线方向,作为一组剪枝方向;其他4个方向为对角线方向,作为另一组剪枝方向,两组剪枝方向分别采用不同的剪枝规则[24]。正方形栅格地图中垂直线方向和对角线方向是交替出现的,借鉴这一特点,在正六边形栅格地图中,将东、西北、西南方向作为一组剪枝方向,该方向采用传统JPS算法中垂直线方向的剪枝规则,将西、东北、东南作为另一组剪枝方向,该方向采用传统JPS算法中对角线方向的剪枝规则。
(1) HJPS算法的邻居剪枝规则
图8是HJPS算法的邻居剪枝示意图。其中,箭头为剪枝方向,灰色栅格为被剪枝的邻居节点所对应的栅格。
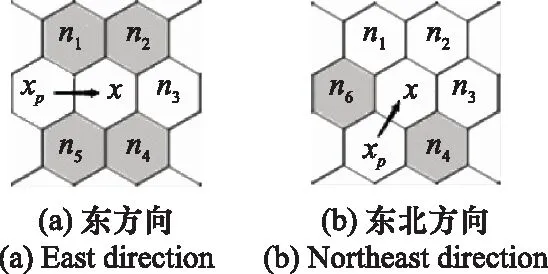
图8 邻居剪枝示意图Fig.8 Schematic diagram of neighbor nodes pruning
当节点x的某一邻居节点ni所在栅格不是障碍物栅格时,若剪枝方向为东、西北或西南方向,且父节点xp经过节点x到邻居节点ni的最短连续节点序列H1以及父节点xp不经过节点x到邻居节点ni的最短连续节点序列H2x满足:
len({xp,x,ni})≥len({xp,…,ni}x)
(2)
则剪枝邻居节点为ni;若剪枝方向为西、东北或东南方向,且满足:
len({xp,x,ni})>len({xp,…,ni}x)
(3)
则剪枝邻居节点为ni。经过剪枝后剩余的邻居节点称为自然邻居。
如图8(a)所示,剪枝方向为东方向,且节点x的邻居节点均不是障碍物栅格的邻居剪枝情况,根据邻居剪枝规则,邻居节点n1、n2、n4、n5被剪枝,邻居节点n3为自然邻居;如图8(b)所示,剪枝方向为东北方向的邻居剪枝情况,根据邻居剪枝规则,邻居节点n4、n6被剪枝,邻居节点n1、n2、n3为自然邻居。
(2) HJPS算法的强制邻居判断规则
当节点x的某一邻居节点ni所在栅格是障碍物栅格时,剪枝结果就会发生变化。比如节点x的邻居节点n1为障碍物栅格,如图9所示,剪枝方向为东方向,与图8(a)的剪枝方向相同。对于邻居节点n2,由图9可知,实线箭头表示的连续节点序列为{xp,x,n2},虚线箭头表示的连续节点序列为{xp,n5,n4,n3,n2}x,根据上述邻居剪枝规则中的式(2),邻居节点n2不再满足被剪枝的条件,此时,邻居节点n2就变成节点x的强制邻居。
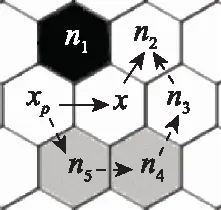
图9 强制邻居示意图Fig.9 Schematic diagram of forced neighbor nodes
综上,HJPS算法的强制邻居判断规则为:在邻居剪枝的基础上,节点x的某一邻居节点ni所在栅格是障碍物栅格时,若其他非障碍物的某一邻居节点nj,(j≠i),不是节点x的自然邻居,且父节点xp经过节点x到邻居节点nj的最短连续节点序列H3以及父节点xp不经过节点x到邻居节点nj的最短连续节点序列H4x满足:
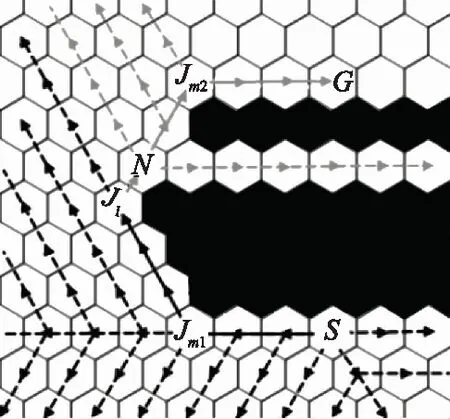
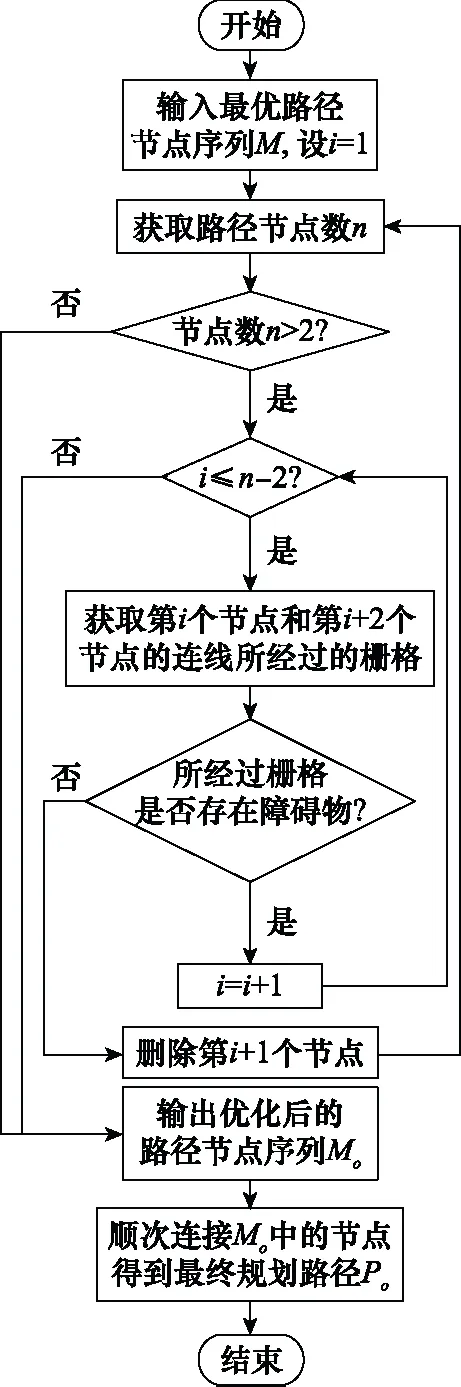
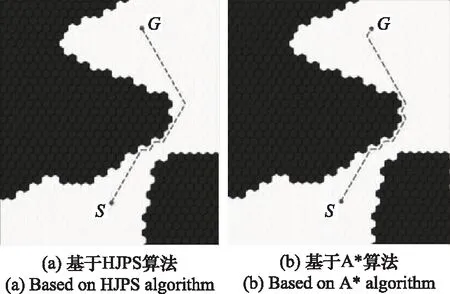
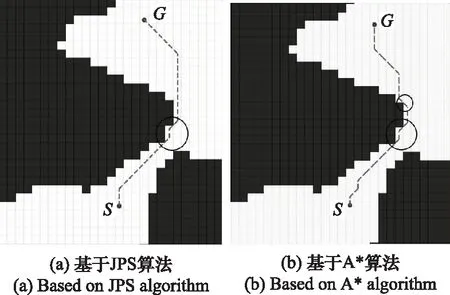
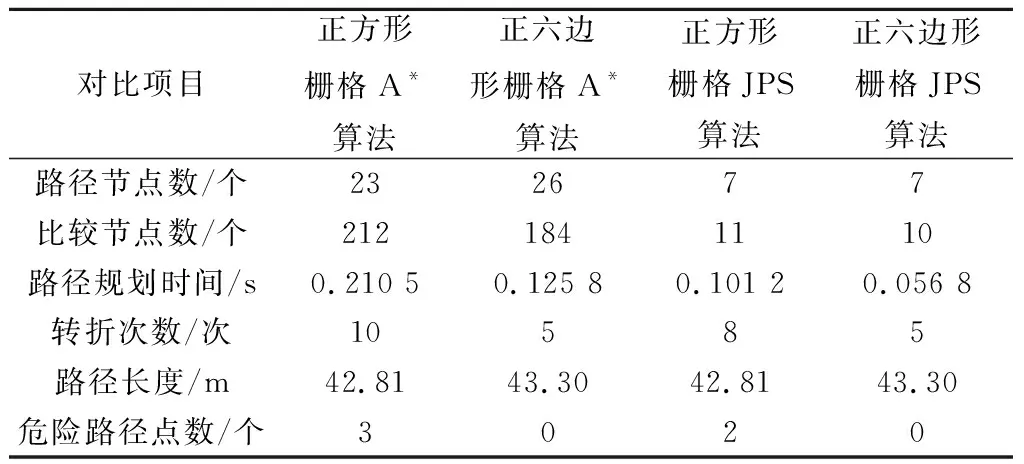
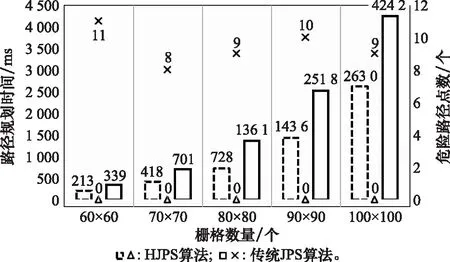
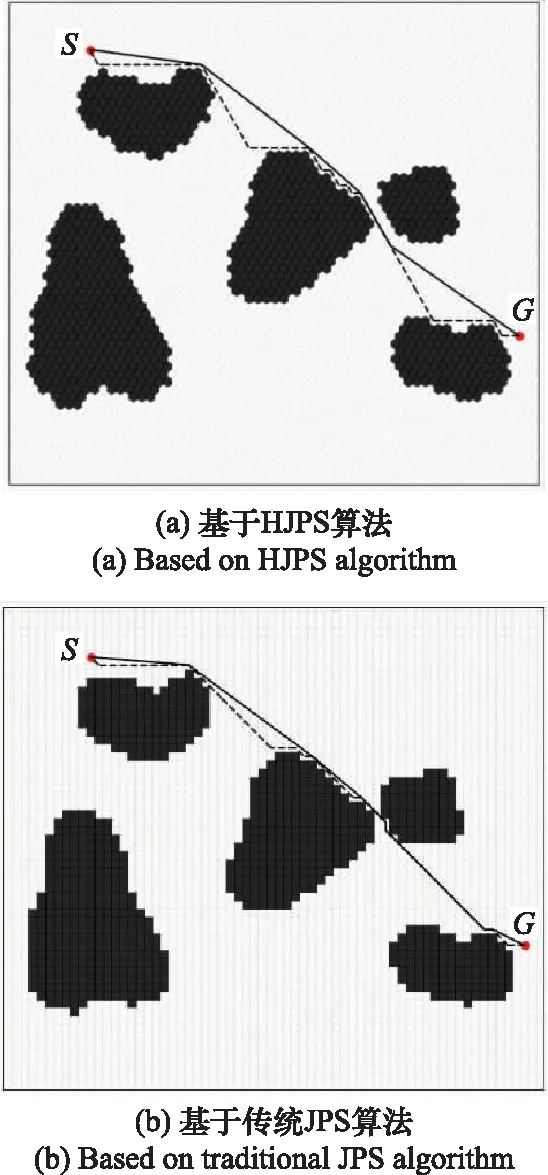
len({xp,x,nj}) (4) 则该邻居节点nj是节点x的强制邻居。当节点x存在强制邻居时,节点x就被定义为跳点。 传统JPS算法搜索跳点作为后继节点加入到OPEN列表中。在正方形栅格地图中,垂直线和对角线方向上均有强制邻居和跳点,因此,传统JPS算法既要在垂直线和对角线方向上搜索伴有强制邻居的跳点,也要在对角线方向分支出的两个方向上搜索伴有强制邻居的跳点[25]。 根据HJPS算法修改后的邻居剪枝和强制邻居判断的规则可知:在正六边形栅格地图中,东、西北和西南方向上会出现强制邻居和跳点,因此将其作为一组搜索方向,定义为方向Ⅰ,如图10(a)实线箭头所示;西、东北和东南方向上不出现强制邻居和跳点,因此将它们作为另一组搜索方向,定义为方向Ⅱ,如图10(a)虚线箭头所示。 搜索方向确定后,HJPS算法的跳点搜索策略为:① 目标点作为目标跳点被搜索;② 为避免重复遍历栅格地图中的节点,在方向Ⅰ上搜索伴有强制邻居的跳点或目标跳点,如图10(b)实线箭头所示;③ 也在方向Ⅱ上的节点分支出的两个方向上搜索伴有强制邻居的跳点或目标跳点,如图10(b)虚线箭头所示,若在方向Ⅱ上的某节点分支出的两个方向上搜索到伴有强制邻居的跳点或目标跳点,则定义该节点为中间跳点。 图10 HJPS算法的跳点搜索策略Fig.10 Jump point search strategy of HJPS algorithm 由于因为HJPS算法在方向Ⅱ进行邻居剪枝时不产生强制邻居和跳点,因此该算法在方向Ⅱ搜索时只需要在其分支出的两个方向上搜索跳点即可,这简化了跳点搜索策略,提高了HJPS算法的运行效率。 图11为HJPS算法的JPS过程示意图,图中S和G分别为起点和目标点,虚线和实线分别为未搜索到跳点和搜索到跳点的过程,灰色虚线为跳点指向强制邻居的方向Ⅱ的搜索过程。 图11 HJPS算法的JPS过程示意图Fig.11 Schematic diagram of JPS process of HJPS algorithm 利用HJPS算法搜索S至G的最优路径节点序列M的流程如下。 步骤 1输入起点S和目标点G的栅格节点坐标。 步骤 2创建OPEN列表和CLOSE列表,分别存放跳点和构成最终路径的跳点。每个跳点的距离成本函数F(j)计算公式为 F(j)=G(j)+H(j) (5) 式中:G(j)为起点到跳点j的实际距离,若起点至跳点j之间无其他跳点,则G(j)为两点之间的直线距离,若其存在其他跳点,则G(j)为起点经过其他跳点至跳点j的分段直线距离的累加;H(j)为跳点j到目标点的启发式距离[26],启发式距离是指跳点j至目标点的最优路径的估计距离,可由跳点j至目标点的直线距离表示。 步骤 3将起点作为初始跳点加入CLOSE列表。 步骤 4取初始跳点指向非障碍物的邻居节点的方向为当前搜索方向,根据当前搜索方向利用跳点搜索策略搜索所有满足条件的跳点,搜索到跳点后结束当前搜索方向的搜索过程。 步骤 5设初始跳点为搜索到的所有跳点的父节点,并将搜索到的跳点加入OPEN列表。 步骤 6将OPEN列表中新加入的所有跳点中F(j)值最小的跳点设为当前跳点,并移到CLOSE列表中。 步骤 7判断当前跳点是否为目标点,若是,将CLOSE列表中的所有跳点作为最优路径节点序列M输出,HJPS算法结束;若否,进行下一步。 步骤 8取当前跳点的父节点指向当前跳点的方向为剪枝方向,根据剪枝方向利用HJPS算法的邻居剪枝规则剪枝当前跳点的邻居节点。 步骤 9取当前跳点指向经过剪枝后剩余的邻居节点的方向为当前搜索方向,根据当前搜索方向利用JPS策略搜索所有满足条件的跳点,搜索到跳点后结束当前搜索方向的搜索过程。 步骤 10设当前跳点为搜索到的所有跳点的父节点,并将搜索到的跳点加入OPEN列表,回到步骤6。 如图11所示,按照HJPS算法的流程,从初始跳点开始,利用第2.2节中的邻居剪枝和强制邻居判断的规则,可以判断节点N为强制邻居,利用第2.3节中的跳点搜索策略,可以搜索到伴有强制邻居N的跳点J1、中间跳点Jm1和Jm2、目标跳点G,最终得到起点S至目标点G的最优路径节点序列M={S,Jm1,J1,Jm2,G}。 利用HJPS算法解决在存在障碍物的环境地图上的智能体路径规划问题的流程如下。 步骤 1对环境地图进行正六边形栅格化建模。 步骤 2确定智能体路径规划的起点S和目标点G所在的栅格坐标。 步骤 3利用HJPS算法搜索S至G的最优路径节点序列M。 步骤 4顺次连接M中的节点得到S至G的规划路径P,输出P作为所规划的智能体路径,路径规划结束。 由于正六边形栅格地图中6个搜索方向的限制,规划路径P可能存在阶梯线或锯齿线[27],如图12所示,这样的路径存在转折次数多、转向角度大的问题。针对该问题,可利用弗洛伊德路径平滑算法[28]对最优路径节点序列M进一步优化,得到优化后的路径节点序列Mo,该算法流程图如图13所示,顺次连接优化后的路径节点序列Mo中的节点,便得到智能体的最终规划路径Po。 图12 存在阶梯线的路径示意图Fig.12 Schematic diagram of path with step line 图13 弗洛伊德路径平滑算法流程图Fig.13 Flow chart of Floyd path smoothing algorithm 利用Python语言和Pycharm平台对基于HJPS算法的智能体路径规划进行仿真研究。 仿真 1为验证HJPS算法的有效性以及对比传统JPS算法和A*算法的优越性,在如图14所示的45 m×50 m尺寸的某矩形环境地图进行路径规划仿真,图中白色部分为可行区域,黑色部分为障碍物。 图14 某矩形环境地图Fig.14 A rectangular environment map 设S和G分别为路径规划的起点和目标点,分别构建28×32的相同规格的正六边形栅格地图和正方形栅格地图,并在两种栅格地图上分别利用JPS算法和A*算法进行路径规划,仿真结果如图15和图16所示。有关路径节点数、比较节点数、路径规划时间、转折次数、路径长度和危险路径点数的仿真结果对比如表1所示,表中结果均为50次路径规划仿真结果的平均值,其中比较节点数指添加至OPEN列表进行最小值选取的节点数,危险路径点数指图16中黑色圆圈所示的涉及穿越墙角行为的路径点个数。 图15 基于正六边形栅格地图的路径规划结果Fig.15 Path planning results based on hexagon grid map 图16 基于正方边形栅格地图的路径规划结果Fig.16 Path planning results based on square grid map 表1 路径规划结果对比 由图15(a)可知,HJPS算法能够实现路径规划。由表1可知,基于两种栅格地图的JPS算法所规划路径的节点数均少于基于两种栅格地图的A*算法所规划路径的节点数;两种JPS算法对比A*算法减少了约95%的比较节点数;两种JPS算法运行效率高于A*算法,且HJPS算法对比传统JPS算法减少了约44%的路径规划时间;基于正六边形栅格地图所规划路径的转折次数比基于正方形栅格地图所规划路径的转折次数要少;在同种栅格地图中基于A*算法和两种JPS算法所规划路径的长度相等,基于正六边形栅格地图所规划的路径比基于正方形栅格地图所规划的路径长约1%。对比图15和图16中基于两种栅格地图所规划的路径以及表1中的危险路径点数,基于正六边形栅格地图所规划的路径避免了穿越墙角的不安全行为,离障碍物的距离更加安全合理,因此危险路径点数为0。 仿真 2为进一步对比HJPS算法和传统JPS算法的性能,对如图17所示的50 m×50 m尺寸的障碍物分布较复杂的某正方形环境地图进行路径规划仿真。 图17 某正方形环境地图Fig.17 A square environmental map 设S和G分别为路径规划的起点和目标点,分别构建60×60至100×100的不同规格的正六边形栅格地图和正方形栅格地图,并利用HJPS算法和传统JPS算法分别进行路径规划仿真,该仿真过程使用弗洛伊德路径平滑算法。 不同规格的栅格地图下HJPS算法和传统JPS算法在路径规划时间和危险路径点数两个性能指标下的对比如图18所示。由图18可知,HJPS算法对比传统JPS算法在不同规格的栅格地图下均减少了约40%的路径规划时间,且危险路径点数均为0。其中,60×60栅格地图下的路径规划仿真结果如图19所示,基于传统JPS算法和弗洛伊德路径平滑算法所规划的路径存在11个危险路径点,而基于HJPS算法和弗洛伊德路径平滑算法所规划的路径均与障碍物保持了一定的安全距离,无危险路径点。可见,HJPS算法对比传统JPS算法,能够规划出更为安全合理的路径,同时路径规划速度更快。 图18 HJPS算法和传统JPS算法性能对比Fig.18 Performance comparison of HJPS algorithm andtraditional JPS algorithm 图19 60×60栅格地图下路径规划结果Fig.19 Path planning results under 60×60 grid map 针对传统JPS算法规划出的路径存在穿越墙角的不安全行为的问题,本文构建正六边形栅格地图,修改传统JPS算法的邻居剪枝、强制邻居判断的规则和JPS策略,提出正六边形栅格JPS算法,并利用该算法解决智能体在障碍物分布较为复杂的环境地图中的路径规划问题。以智能体为对象进行路径规划仿真比较,验证了所提算法的有效性和优越性。正六边形栅格JPS算法能够利用JPS算法路径规划效率高以及正六边形栅格地图可避免穿越墙角的不安全行为的特点,提高路径规划的质量和效率。 本文所提出的正六边形栅格JPS算法可推广应用于无人车、无人机、无人船等智能化无人装备在复杂环境下的路径规划问题。2.3 HJPS算法的跳点搜索策略
2.4 HJPS算法流程
3 基于HJPS算法的智能体路径规划

4 仿真研究


5 结 论

