极化合成孔径雷达有源干扰的干信比方程

牛朝阳, 王建涛, 胡 涛, 刘 伟, 李润生

(战略支援部队信息工程大学, 河南 郑州 450001)

0 引 言

在复杂战场环境下,为了能够隐蔽己方重要目标、迷惑对方雷达以保障战役和战斗的胜利,针对对方雷达实施战略或战术上的电子干扰具有重要军事意义[1]。国内外已经就合成孔径雷达(svnthetis aperture radar, SAR)以及常规单极化SAR(polarimetric SAR, PolSAR)电子战问题进行了广泛研究[2-3],提出了多种干扰方式和具体方法,包括有源压制干扰、有源欺骗干扰、无源干扰等[4-13],而对PolSAR系统干扰的研究鲜有报道。近年来,许多国家纷纷研制或装备了PolSAR系统[14-15],通过对电磁波极化信息的利用,有效提高雷达的目标检测、目标识别、抗干扰等能力。由于PolSAR全极化工作体制的特殊性,单PolSAR干扰技术用于PolSAR时难以奏效,一是单极化噪声压制干扰对PolSAR极化散射矩阵的干扰是不充分的,可以通过极化对消技术予以抑制[3,16-17];二是单极化假目标与真实雷达目标的极化散射特性存在较大差异,从而使其在各种极化鉴别器面前无处遁形[16-21]。鉴于上述原因,推进开展针对PolSAR干扰技术的相关研究具有重要意义[16,22]。

需要特别指出的是,针对PolSAR这一新体制SAR的电子干扰,既需要立足于现有常规单PolSAR电子干扰的理论和技术体系,更需要针对该课题存在的问题进行理论突破和技术创新。PolSAR测量的是能够完整描述地物目标极化特性的极化散射矩阵,对PolSAR地物目标信息的提取与处理也正是基于极化散射矩阵展开的,所以对PolSAR的电子干扰也应该面向PolSAR极化散射矩阵。在这一点上,现有的常规单PolSAR电子对抗技术体制是无法解决的。解决PolSAR电子干扰问题的基础首先需要建立针对PolSAR电子干扰的雷达方程。

本文首先在分析传统单PolSAR方程的基础上,推导了目标和杂波的PolSAR信噪比方程,这对下一步进行PolSAR电子干扰的原理分析具有重要意义;干扰波与PolSAR天线系统之间的极化匹配问题是影响有效干扰功率的重要因素,因此本文紧接着定义和分析了干扰电磁波与PolSAR接收天线系统之间的极化匹配因子,推导了PolSAR接收天线系统之间的复极化比关系,并在此基础上构建了PolSAR系统接收机端输出的干扰方程,分3种情况建立了PolSAR成像处理后的干扰方程;最后本文利用建立的干扰方程,对不同极化合成干扰波的PolSAR干扰效果进行了深入阐述。

1 SAR与PolSAR方程构建

雷达方程是反映雷达系统参数、目标参数及其空间位置关系的基本方程,其作用在于:一是估计已完成设计或已投入使用的雷达系统作为目标探测装置的性能,如最大作用距离、最小可探测目标等;二是辅助设计雷达系统,根据规定的作用距离,正确选择、分配各分系统指标,如确定雷达发射功率、接收机噪声系数、数据采集系统动态范围等参数;三是用于雷达系统的辐射定标;四是在此基础上可以进一步推导雷达干扰方程。因此，本节在传统单PolSAR方程的基础上,推导给出PolSAR的目标和杂波信噪比方程,为下文推导PolSAR干扰方程铺垫基础。

1.1 传统SAR雷达方程

(1) 接收机输出的信噪比

对传统单站SAR,雷达、目标与干扰机的空间位置如图1所示。雷达平台沿虚线向右方飞行,雷达天线的方位向孔径长度为D,雷达合成孔径中心位置与地面某目标之间的斜距为R,雷达合成孔径中心位置与干扰机之间的斜距为Rj,相对波束角为θj。

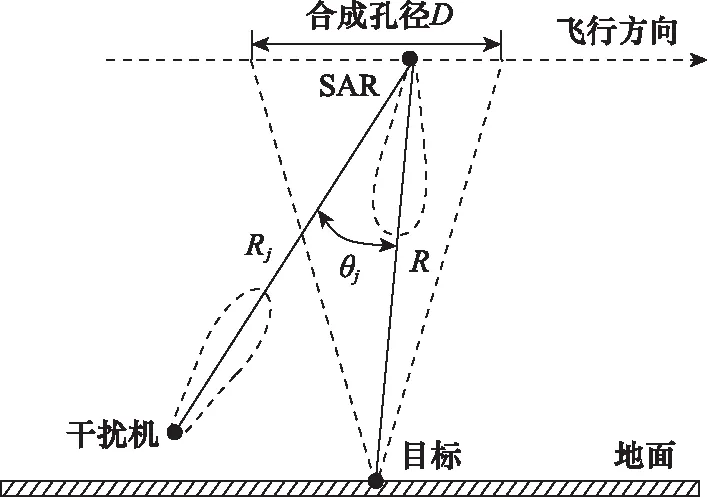
图1 雷达、目标与干扰机三方的空间几何关系示意图Fig.1 Schematic diagram of spatial geometric relationship among radar, target and jammer

设发射和接收天线的功率增益均为G,目标的雷达散射截面积(radar cross section, RCS)为σ,则雷达接收机输出的目标信号功率[23-24]为

(1)

式中：Pt为雷达发射功率；λ为雷达工作波长；Ls为雷达接收机系统损耗；La为雷达与目标之间的双程链路损耗[25]。

SAR接收机系统产生的热噪声功率为

Nreceiver=kT0B

(2)

式中：k为玻尔兹曼常数；T0为接收机系统噪声温度；B为雷达系统带宽(设与雷达信号带宽一致)。所以传统SAR接收机末级中放输出信噪比为

(3)

式中:Fn为接收机噪声系数。

(2) 成像处理后的信噪比

(4)

SAR接收机系统噪声功率经成像处理获得的距离向和方位向增益分别为nr和na,即

(5)

SAR系统成像处理输出的信噪比为

(6)

式中:Pav=Ptfrτ为SAR系统的平均发射功率。对于SAR测量的地面杂波,其RCS是归一化的杂波散射系数σ0与雷达地面距离向分辨率ΔRg和方位向分辨率ΔAg的乘积[26],即

σ=σ0ΔRgΔAg

(7)

式中：ΔRg=c/(2Bcosβg)，c表示光速；βg为雷达目标处的入射波擦地角;条带聚焦模式下ΔAg=D/2。

将式(7)代入式(6),并化简,可得成像处理后的SAR杂波噪声比CNR为

(8)

1.2 PolSAR方程

在推导PolSAR方程时应该详细说明发射和接收天线的极化状态,第1.1节给出的SAR方程忽略了这一点[24],并不能够完全描述目标的极化散射特性。在前文对传统单PolSAR方程与PolSAR系统工作原理分析的基础上,本节对PolSAR方程进行推导。

(1) 接收机输出的信噪比

设单站PolSAR系统工作在相互正交的x和y线极化方式下,用极化散射矩阵元素来描述目标的RCS[23],则不同极化组合下的目标RCS可写成如下的矩阵形式：

(9)

式中：σxy=σyx;sxy=syx。

将式(9)代入式(1),可将PolSAR接收机末端输出的不同极化状态组合的信号功率写成如下的矩阵形式：

(10)

式中：⊙表示两个矩阵的hadamard积；*表示矩阵的共轭。

通常情况下,可假定PolSAR接收机系统产生的热噪声功率是不依赖于发射天线和接收天线极化状态的,其大小仍可由式(2)确定,则PolSAR接收机末端输出信噪比为

(11)

(2) 成像处理后的信噪比

PolSAR成像处理在本质上是二维匹配滤波过程,目标信噪比也将获得nrna倍增益。因此,经过成像处理后的PolSAR目标信噪比为

(12)

对于PolSAR系统测量的杂波,归一化的杂波散射系数σ0是一种非相干目标参数,通常采用空间多视平均的形式[23]进行表示:

(13)

式中：〈·〉表示求集合平均。

将式(7)和式(13)代入式(8),可得到以矩阵形式描述的PolSAR图像杂波噪声比为

(14)

式(12)与以矩阵的形式给出了接收机输出和成像处理两个阶段的PolSAR方程,与极化散射矩阵联系起来完整地描述了不同极化状态组合下的信噪比和杂波噪声比,不仅可以通过极化基变换获得任意极化基下的信噪比和杂波噪声比,还可以用于PolSAR目标探测性能的理论分析。

2 PolSAR电子干扰方程构建

干扰方程对于电子干扰机设计和干扰效果评估具有重要意义。现有的SAR干扰方程[26,28]是基于单极化通道工作体制的,对于通过4个极化通道测量目标散射特性的PolSAR,无法全面反映对其实施电子干扰的干扰功率需求。为此,本节以交替发射同时接收工作体制的PolSAR为例,对PolSAR电子干扰的功率方程进行推导。

2.1 PolSAR电子干扰的极化匹配因子

在特定的坐标系下,设干扰波的Jones矢量和雷达接收天线在干扰波方向上的有效长度分别是E和h,则干扰波在雷达接收天线上凹口处感应的开路电压可以表示为

V=ETh=|E|·|h|cosβ

(15)

式中：β(-π/2≤β<π/2)为两个矢量E和h的交角。在Poincaré球[29]上,β是干扰波极化状态点与雷达接收天线极化状态点的共轭点之间的球心角的一半。

极化匹配因子[30]为雷达接收天线实际接收的功率与最佳极化匹配条件下接收的功率之比。按照此定义,可将干扰波与雷达接收天线之间的极化匹配因子γ写为

(16)

式中：Pr表示雷达接收天线实际接收的干扰信号功率；Pmax表示在最佳极化匹配条件下雷达接收天线接收的干扰信号功率。极化匹配因子γ表示了干扰波与有效长度为h的雷达接收天线极化匹配的良好程度。显然,γ的取值范围为0≤γ≤1,当二者极化方式匹配时,γ取最大值,当二者极化方式正交时,γ取最小值。

图 2是干扰波与雷达接收天线之间的极化匹配因子随β变化曲线图。当用线极化天线接收圆极化干扰波或者用圆极化天线接收线极化干扰波时,在Poincaré球上有β=45°,因此γ=-3 dB,这些带来3 dB损失的情况在雷达对抗领域是常见的。

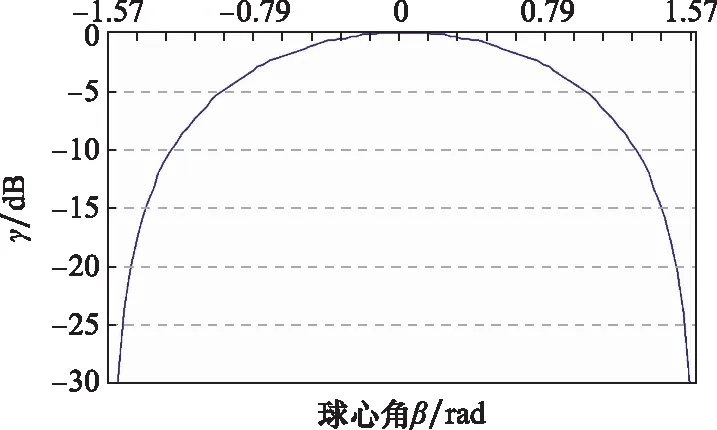
图2 干扰波与雷达接收天线之间的极化匹配因子变化曲线图Fig.2 Change curve of polarization matching factor between interference wave and radar receiving antenna

在上面的理论推导中,当干扰波与PolSAR接收天线极化正交时,得到的结果将是极化匹配因子γ=-∞ dB。但是在实际的天线系统中,由于制作工艺或者结构上的原因,使得正交极化的收发之间不可能做到完全隔离,总存在着极化泄漏,不过泄漏的功率非常微弱,一般不需要考虑。

2.2 PolSAR接收天线的复极化比关系

设ρj与ρr分别表示干扰机天线和雷达接收天线的复极化比,在雷达收发天线分别采用一个右旋坐标系[30]的情况下,式(16)所示的极化匹配因子γ可改写为

(17)

对于PolSAR,设相互正交的x和y极化接收天线的复极化比分别为ρx和ρy,若复极化比为ρj的干扰波与复极化比为ρx的PolSAR接收天线是极化匹配的,即γ=1,由式(18)可得

(18)

则另一个PolSAR接收天线是与干扰信号极化正交的,即γ=0,由式(17)可得

(19)

因此,一对极化正交的PolSAR接收天线复极化比之间的关系如下:

(20)

式(20)就是两个极化正交的PolSAR接收天线所满足的复极化比关系,与式(19)所示的收发天线极化正交时的复极化比关系相比,不同之处在于多了复共轭的关系。这是由于在分析复极化比以及极化匹配因子时,发射天线与接收天线之间的坐标系是不同的,使得极化电磁波的旋向相反。

2.3 PolSAR接收机输出端的干扰方程

在单站PolSAR的电子干扰中,雷达、目标与干扰机的空间位置如图1所示,PolSAR天线以其主瓣波束指向目标,干扰机发射天线以其主瓣波束指向PolSAR。PolSAR接收天线在干扰机方向的增益均为G(θj)。全极化干扰机工作在相互正交的u、v线极化状态下,不断地向被干扰PolSAR发射两路极化正交的干扰信号,天线增益均为Gj。

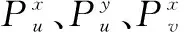
(21)

(22)

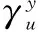
PolSAR所测量的散射矩阵元素syx对应的干扰波功率,为PolSAR发射x极化脉冲信号并在y极化天线上接收到的u极化和v极化干扰波功率之和：

(23)

同理,可得PolSAR所测量的其他3个散射矩阵元素对应的干扰波功率：

(24)

(25)

(26)

从而,在一次完整的极化散射矩阵测量中,与散射矩阵元素对应的4个干扰信号功率可以写成如下的矩阵形式：

(27)

记

(28)

(29)

分别为全极化干扰机的发射功率矩阵和极化匹配因子矩阵,则式(27)可简记为

(30)

那么,在一次完整的极化散射矩阵测量中,PolSAR接收天线系统能够接收到的有效干扰总功率为干扰功率矩阵J所有元素之和：

(31)

同一干扰波在被PolSAR接收天线系统接收时,结合式(17)、式(19)和式(20),可得

(32)

将式(32)代入式(29)中有：

(33)

因此,式(27)与式(31)分别变成

(34)

(35)

式(34)与式(35)即是PolSAR系统接收机输出端的干扰功率方程,根据可以得到PolSAR电子干扰有效功率的能量分配与守恒规律:① 在一次完整的极化散射矩阵测量中,干扰机的极化配置影响干扰功率在4个极化散射矩阵元素上的分配形式;② 有效干扰总功率依赖于干扰机的发射功率和天线增益,而与干扰机和PolSAR天线系统的极化基无关;③ 在PolSAR接收时间窗口内,由于PolSAR的全极化收发体制,干扰功率总能够完全进入PolSAR系统。

对传统单极化SAR进行干扰时,若干扰信号与SAR天线极化不匹配,总会在SAR接收天线处损失部分干扰功率,这与上述第3点结论显然不同。

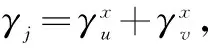
(36)

(37)

2.4 PolSAR成像处理后的干扰方程

参照SAR非相干干扰和相干干扰的定义[28],PolSAR非相干干扰和相干干扰分别指干扰机发射的干扰信号与PolSAR工作信号不相干和相干。由于相干干扰信号经成像处理后获得的增益与非相干干扰信号相比显著提高,所以PolSAR相干干扰在干扰效果上较非相干干扰有明显的优势,但依赖于对PolSAR工作频率、脉冲宽度、脉冲重复频率等工作参数,实现起来较为复杂。

(1) 非相干干扰方程

若全极化干扰机发射的干扰信号与PolSAR回波信号完全不相干,经过PolSAR成像处理后,干扰信号功率与系统噪声功率获得的处理增益均为nrna。因此，由式(30)可得非相干干扰下PolSAR成像后干扰与噪声功率比为

(38)

式中:下标“IN”表示非相干干扰。将式(38)分别与式(12)和式(14)相比,可得PolSAR成像后干信比JSR与干杂比JCR分别为

(39)

(40)

式中：

FJSR=Pγ./〈S⊙S〉

(41)

FJCR=Pγ./〈S⊙S〉

(42)

分别为对应方程的干信比因子矩阵和干杂比因子矩阵,“./”表示矩阵的对应元素相除。

(2) 部分相干干扰方程

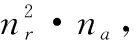
(43)

式中:下标“PC”表示部分相干干扰。这里未考虑分摊损失因子[29],因为无论是非相干干扰、部分相干干扰还是完全相干干扰,干扰能量在图像中的分布区域大小,正是其所获得的成像处理增益不同的体现。

将式(43)分别与式(12)和式(14)相比,可得PolSAR成像后干信比JSR与干杂比JCR分别为

(44)

(45)

(3) 完全相干干扰方程

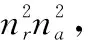
(46)

式中:下标“FC”表示完全相干干扰。将式(46)分别与式(12)和式(14)相比,可得PolSAR成像后干信比JSR与干杂比JCR分别为

(47)

(48)

综合式(39)、式(40)、式(44)、式(45)、式(47)和式(48)可以看出,在非相干、部分相干与完全相干3种情况下,PolSAR成像后的干信比与干杂比表达式均包含干扰机发射功率矩阵P、极化匹配因子矩阵γ和极化散射矩阵S。因此可知,PolSAR成像后各个通道的干信比与干杂比不仅依赖于干扰总功率在各个通道PolSAR图像的分布形式,而且受制于干扰机在各通道干扰信号的极化配置,同时也与PolSAR目标的极化散射矩阵有关(由式(12)和式(14)可知,即与各通道PolSAR目标功率和杂波功率相关)。

另外,将式(44)和式(47)分别与相比可得到JSRPC=nrJSRIN、JSRFC=nrnaJSRIN,式(45)和式(48)分别与相比可得JCRPC=nrJCRIN、JCRFC=nrnaJCRIN。因此,与非相干干扰相比,部分相干干扰干信比和干杂比获得的增益为nr,完全相干干扰干信比和干杂比获得的增益为nrna。

(4) 干扰方程的仿真分析

由第2.3节可知,PolSAR成像后各个通道的干信比和干杂比依赖于干扰机发射功率矩阵P、极化匹配因子矩阵γ和极化散射矩阵S,且在非相干、部分相干与完全相干3种情况下具有相似性,因此这里仅以非相干干扰的情况为例对干信比进行仿真分析,基本参数设置情况见表1。

表1 仿真参数设置表

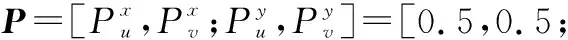
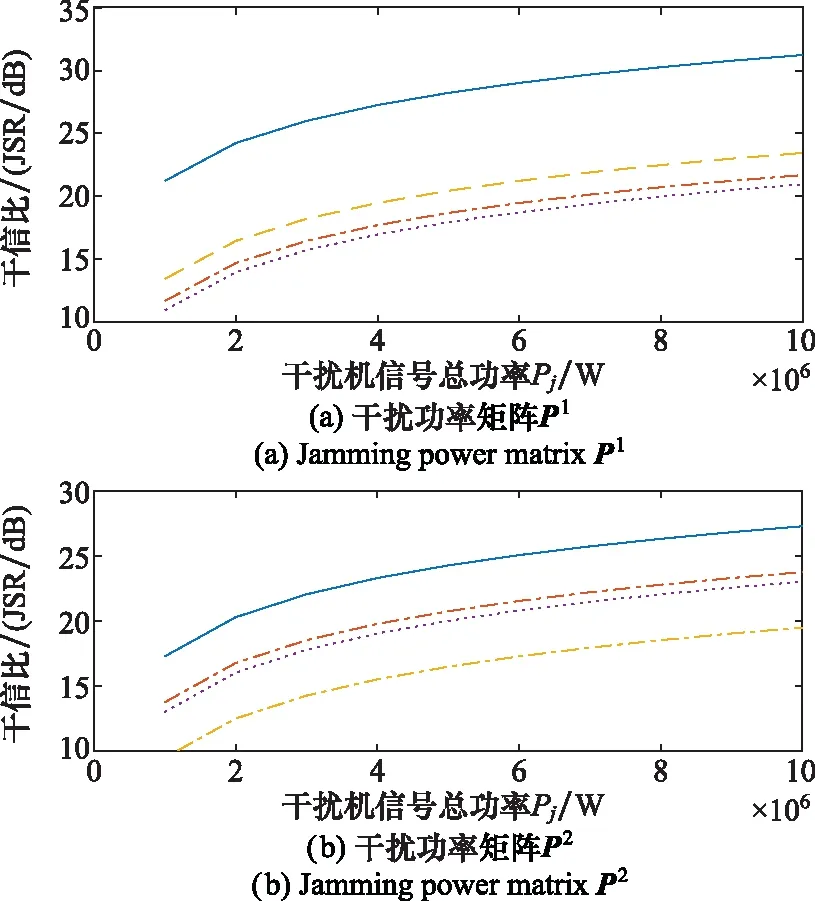
实验 2设置1个目标,其极化散射矩阵为S2=[5,15;15,20];干扰机功率Pj在1～10 MW区间增加,干扰机功率配置分别设为P1=[0.5,0.5;0.5,0.5]×Pj、P2=[0.2,0.2;0.8,0.8]×Pj、P3=[0.7,0.7;0.3,0.3]×Pj;极化匹配因子矩阵设为γ=[0.35,0.65;0.45,0.55]。根据表1和式(39)计算出不同目标极化散射矩阵的干信比JSR,如图4所示。PolSAR成像后同一目标的干信比,在相同的干扰信号极化匹配因子矩阵条件下,取决于干扰功率配置矩阵,即干扰机功率在各通道干扰信号的分配方式。

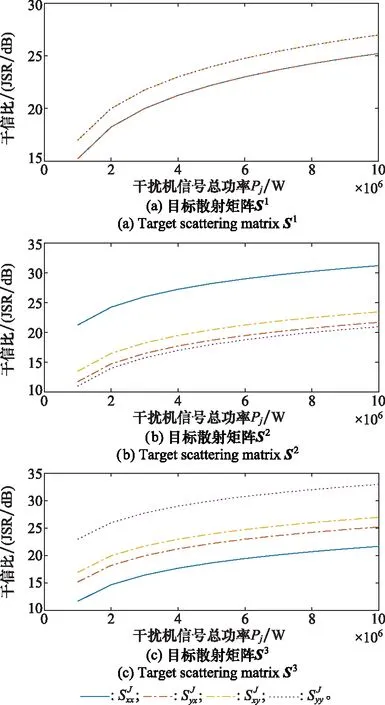
图3 不同目标极化散射矩阵下的JSR曲线图 Fig.3 The curve of JSR for different polarimetric scattering matrices

实验 3设置1个目标,其极化散射矩阵为S3=[15,10;10,5];干扰机功率Pj在1～10 MW区间增加,干扰机功率配置分别设为P=[0.5,0.5;0.5,0.5]×Pj;极化匹配因子矩阵分别设置为γ1=[0.35,0.65;0.45,0.55]、γ2=[0.75,0.25;0.15,0.85]、γ3=[0.05,0.95;0.40,0.60]。根据表1和式(39)计算出不同目标极化散射矩阵的干信比JSR,如图5所示,PolSAR成像后同一目标的干信比,在相同的干扰机功率配置条件下,取决于干扰信号极化匹配因子矩阵,即各通道干扰信号与PolSAR接收天线极化方式之间的极化匹配因子。

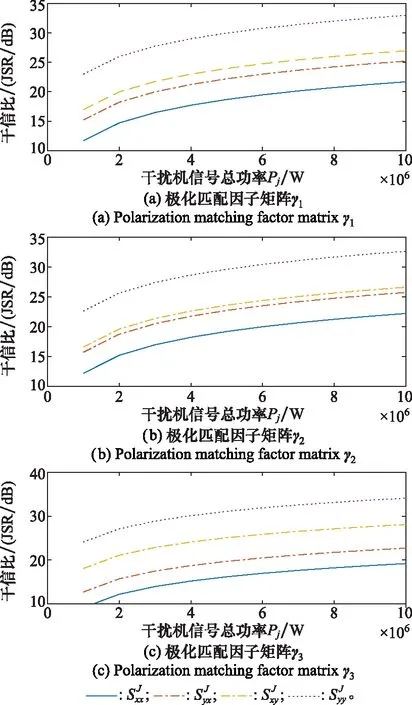
图5 不同极化匹配因子矩阵下的JSR曲线图 Fig.5 The curve of JSR for different polarization matching factor matrices

3 不同极化合成干扰波的干扰效果

由电磁场与电磁波理论[30-31]可知,任意极化均可由一对正交极化以不同的幅度比和相位差相合成。在原理上,发射时可将同一信号源经功分器后,经过不同的幅相关系处理分别送到一对极化正交的天线,便可合成任意极化状态。所以,全极化干扰机的两路极化正交的干扰波将在空间中合成一路干扰波,在不同的相位和幅度下合成的干扰波有着不同的极化状态,其对PolSAR干扰性能差异较大。

3.1 单极化方式的干扰

如果全极化干扰机的两路干扰波完全相干,其将在空间中合成单一极化状态的干扰波,此时干扰效果等同于传统单PolSAR干扰机。设合成干扰波的极化状态为z,与PolSAR的x极化和y极化接收天线之间的极化匹配因子分别为γz和1-γz,可得到式(34)的一个特例

(49)

式中：下标“SP”表示完全极化。当合成干扰波的极化状态z与x极化PolSAR接收天线相匹配时,γz=1,式(49)变为

(50)

这种情况下,电子干扰只能对PolSAR的目标极化散射特性形成局部干扰:z极化合成干扰波功率能够全部进入x极化的PolSAR接收天线,从而对两个极化散射矩阵元素(sxx与sxy,xy表示y极化发射x极化接收)形成干扰。而正交极化之间的隔离度[30]在理想情况下趋向于无穷大,z极化状态合成干扰波的功率无法进入y极化的PolSAR接收天线,因此对另外两个极化散射矩阵元素(syy与syx)难以造成影响。当合成干扰波的极化状态z与x极化的PolSAR接收天线相匹配时,γz=0,与γz=1的情况恰恰相反,只能对syy与syx形成干扰。

当合成干扰波的极化状态z与两个PolSAR接收天线均失配时,0<γz<1,式(49)中干扰功率矩阵元素均不为0,此时能够对PolSAR极化散射矩阵的4个元素均构成干扰。但是这种干扰可以通过极化识别、极化滤波以及变极化技术予以抑制[16,32]。

3.2 全极化方式的干扰

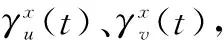
(51)

式中：下标“NP”表示完全非极化。式(51)表明,在完全非极化干扰波对PolSAR干扰的情况下,由于PolSAR全极化的工作体制,两个相互极化正交的接收天线均受到干扰影响,也就是对PolSAR目标极化散射矩阵的4个通道(即4个元素sxx、sxy、syx与syy)均形成干扰。所以，这种干扰相比单一极化状态的干扰波,能够全面干扰PolSAR测量的极化散射矩阵,且由于干扰波的极化状态是完全随机的,对PolSAR所测量的散射矩阵元素的影响也是完全随机的。

3.3 部分极化方式的干扰

如果全极化配置的干扰机两路干扰波部分相干,则其在传播空间中构成部分极化干扰波,有统计平均意义上的极化状态,实际的极化状态是在平均极化附近随机摆动。根据电磁场和电磁波理论可知,部分极化波可分解为一个完全非极化波和一个完全极化波之和。由部分极化波的Stokes向量表示理论[23],设部分极化干扰信号的极化度为η,综合式(49)和式(51)可得部分极化方式下PolSAR系统接收机输出端的干扰功率为

JPP(t)=ηJSP+(1-η)JNP(t)

(52)

式中：下标“PP”表示部分极化。式(52)包含两项干扰功率,第一项ηJSP为完全极化波的干扰效果,即第3.1节中探讨的单极化方式的干扰效果;第二项(1-η)JNP(t)为完全非极化干扰波的干扰效果,可以参照第3.2节的分析。综合以上分析可知,部分极化干扰波对PolSAR目标极化散射矩阵的影响显然也是全面的,但是这种极化配置的干扰方式中完全极化波分量在一定程度上降低了实际干扰效果。

4 结 论

本文从传统单极化SAR方程出发,系统地构建了PolSAR系统接收机输出的干扰方程与非相干干扰、部分相干干扰和完全相干干扰3种情况下成像处理后的干扰方程,并分析得到了PolSAR电子干扰有效功率的能量分配与守恒结论。该结论的意义在于:对PolSAR的电子干扰效能不仅依赖干扰机的干扰总功率,还需要合理分配全极化干扰机各路干扰能量,才能得到最佳干扰效果。

进一步,基于本文建立的PolSAR接收机输出端干扰方程,推导分析了不同极化合成干扰波时PolSAR接收天线能够接收到的有效干扰功率在4个极化通道中的分配形式,指出了单极化干扰PolSAR时的固有缺陷以及全极化干扰时应该注意的问题。分析表明,传统单极化干扰机在面对PolSAR时,干扰效果是不充分的;而全极化配置的干扰机,只要合理设置使其两路干扰信号不完全相干,可以全面干扰PolSAR的极化散射矩阵，这对于干扰机极化状态的配置有重要的指导意义。