基于STFD的轴承多故障信号欠定盲源分离方法*

诸葛航，吕 勇，易灿灿，袁 锐

(武汉科技大学机械自动化学院，武汉 430081)

0 引言

在旋转机械运行过程中，轴承、齿轮是发生故障的主要部位[1]，且设备中多种故障同时出现的情况普遍存在。而在实验室或工厂中由于成本和检测条件的限制，设备上不能安装较多的传感器，所以传感器的数量小于信号源数量的情况非常普遍(欠定情况)。相比于单个故障的情况，复合故障的情况更复杂且更难以处理。而我们通过传感器测得的复合故障信号是各故障源的混叠信号，其传递过程不明确，且包含强烈的噪声，这给复合故障的诊断带来了很大困难[2]。混合利用欠定盲源分离(UBSS)方法,我们可以在传递过程不明确的情况下从信号中提取有用的故障信号，从而很好地处理复合故障的诊断问题。

传统的盲源分离方法，如独立成分分析(ICA)等，只适用于平稳、非高斯且相互独立源的分离，易受噪声影响。这些方法不能适应复杂非平稳的工况，而时频分布(TFD)方法能够得到在故障信号在时频域的信息，可以有效地反映信号的非平稳特征。空间-时频分布(Spatial Time-Frequency Distribution，STFD)方法由二次时频分布(Quadratic time-frequency distribution，QTFD)发展而来，主要是基于Wigner-Ville分布(WVD)定义的，所以STFD具有不需要严格的独立性假设、先验知识，对噪声不敏感，适用于非平稳信号等优点[3]。许多学者将STFD方法应用于到达波方向(DOA)估计，并取得了较好的效果[4-6]，但是目前很少有学者将STFD方法用于盲源分离来对机械复合故障进行诊断。

本文针对旋转机械中存在的滚动轴承多故障的问题提出了基于空间-时频分布的欠定盲源分离方法，实现了轴承多故障源信号的分离，并在时频域对分离后的信号进行分析与比较，从而进行故障诊断与状态检测；最后通过仿真实验与实测信号验证了方法的可行性与有效性。

1 信号模型

位于三维空间中的源(发射器)发出的信号被传感器(接收器)阵列接收时，源信号的特征信息有两个：到达波方向(DOA)和源信号的组合方式。前者的特性一般表现为转向矢量，其具体体现在同一个源信号在遍历传感器阵列时的相位变化[7]。后者通常称取决于信号源的传播方式，一般有瞬时混合模型和卷积混合模型两种[8]。

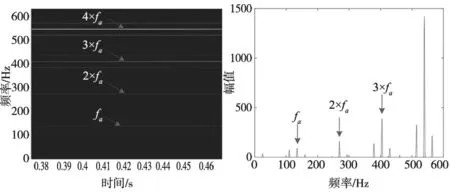
设空间中存在源信号s1,…,sn，它们被传感器阵列观测到，观测信号为x1,…,xm(当m

X=AS+N

(1)

式中，S=[s1,…,sn]T是源信号向量矩阵；X=[x1,…,xm]T是观测信号向量矩阵；N是信号源的噪声；A=[a(θ1),…,a(θn)]是信号传递过程中的混合矩阵或转向矩阵，其中a(θi)=[a1i,…,ami]T是θj方向的转向矢量，i=1,2,…,n。那么：

xj=aj1s1+aj2s2+…+ajmsm+ηj

(2)

式中，j=1,2,…,m；ηj为信号源噪声。

2 空间-时频分布(STFD)原理

2.1 STFD矩阵的计算

传感器采集到的观测信号x1,…,xm，经过Hilbert变换得到解析的向量为z1,…,zm；那么观测信号的二次时频分布(QTFD)可以通过Wigner-Ville分布(WVD)得到：

(3)

其中,i,j=1,2,…,m；(·)*表示共轭转置运算。

通过计算各个观测信号之间以及它们与自身的WVD。将二次时频分布扩展到三维空间中可以得到空间-时频分布(STFD)矩阵，如图1所示(m=3时)：

图1 STFD的原理

图1中，每个时频点(t,f)，都对应一个STFD块矩阵，块矩阵由时频点(t,f)在每个WVD矩阵中对应的位置的值Wzizj(t,f)组成；如STFD(t0,f0)，由Wzizj(t0,f0),i,j=1,2…3组成。所有的时频点对应的STFD块矩阵，组成了完整的空间-时频分布(STFD)矩阵。

2.2 时频点的分类

所有的时频(TF)点分为两类：自动项点与交叉项点。时频点的判断规则如下：

(1)如果WVD矩阵Wzizi在时频点(tp,fp)处存在能量集中，那么(tp,fp)是自动项点，矩阵STFD(tp,fp)是自动项矩阵;

(2)如果WVD矩阵Wzizj(i≠j)在时频点(tq,fq)处存在能量集中，那么(tq,fq)是交叉项点，矩阵STFD(tq,fq)是交叉项矩阵。

自动项是同一源信号的分量之间相互作用形成的，是有用成分，而交叉项是不同的源信号分量之间相互作用形成，属于干扰成分。

2.3 STFD矩阵的白化

基于第一个章节中的信号模型，STFD矩阵有如下结构：

STFDzz(t,f)=ASTFDss(t,f)AH

(4)

其中，STFDss(t,f) 为源信号的STFD矩阵，STFDzz(t,f)代表观测信号的STFD矩阵，假设存在一个白化矩阵W使得：

(WA)(WA)H=UUH=I

(5)

其中，I是单位矩阵，那么U=WA是酉矩阵。利用式(3) ～式(5),可以得到白化后观测信号的STFD矩阵：

(6)

由式(6)可知，白化步骤使原来的线性混合模型转化为酉混合线性模型。而白化矩阵W可以通过计算观测信号数据协方差矩阵的反平方根[9]或者通过STFD矩阵计算得到[10]。

3 基于STFD的轴承多故障信号盲源分离

3.1 计算观测信号的STFD矩阵

盲源分离方法效果的好坏取决于能否正确地筛选出自动项点。为了减少和削弱原始的WVD方法产生的交叉项，增大自动项选择的正确性，我们使用改进的平滑伪Wigner-Ville方法(SPWVD)来计算信号的二次时频分布(QTFD)：

(7)

SPWVD的本质是在WVD的基础上增加了窗函数与平滑函数，它能有效消除交叉干扰项。并且，由于WVD的特性，SPWVD可以将信号的噪声在整个时频域中平均，有较好的抗噪效果。

通过式(7)得到解析信号向量zi(t)与zj(t)的时频矩阵后，根据图1所示方法，可以得到空间-时频分布(STFD)矩阵：

(8)

3.2 噪声阈值处理

为了降低计算的复杂性和时间成本，减少噪声的干扰。在对自动项点和交叉项点进行筛选前，我们对STFD矩阵进行噪声阈值处理，选择性地保留时频域中能量较大的时频点[11]：

(9)

3.3 自动项点的选取

在假设给定源信号时频点在时频域内不重合的条件下，每个自动项TF点对应的STFD矩阵的秩等于1(只存在一个特征值)；若秩不等于1，则它们对应的STFD矩阵的特征值中，存在一个明显较大的特征值[12]。所以秩的多少可以用来区分TF点，即选择STFD 矩阵的秩等于1的TF点作为自动项点。为了简化这一步骤采用如下公式：

(10)

其中，参数ε2是一个可以正标量(一般情况下，ε2=0.3)，λmax{·}是矩阵的最大特征值，norm{·}表示矩阵的范数。

3.4 基于向量集群和源TFD估计

属于同一源信号TF点的STFD矩阵具有相同的主特征向量[12]。我们可以根据这个特点对TF点进行聚类：

(1)对上一节选取的自动项点(ta,fa)的STFD矩阵STFDzz(ta,fa)进行特征值分解，得到主特征向量v(ta,fa)及特征值λ(ta,fa)。

(2)使用k-means算法将步骤(1)中得到的v(ta,fa)集群到不同的类；此时同类时频点对应同一个源。

(3)对每个类的自动项点在时频域内进行排序，得到估计源信号的时频分布(TFD)。

3.5 源信号重建与故障源的定位

根据WVD的反演特性[13]我们可以从源信号的TFD中恢复时域的源信号：

(11)

(12)

式中，cov(·)表示方差；i=1,2,…,n；j=1,2,…,m。距离故障源越近，观测信号与故障源信号的相关系数ρi,j越大，这样我们就可以对故障源的位置进行定位。

本方法在时频域内对信号进行了降噪与盲源分离。与传统的基于时频分析(如Cohen类时频分布、分数Fourier变换等)的盲源分离方法相比较，本方法既适用于处理欠定型盲源分离问题，也适用于处理超定型盲源分离问题。而传统的基于时频域的盲源分离往往具有一定的局限性，只能处理单一的情况。并且与协方差矩阵法相比本方法能够有效的提高信噪比，从而提高对噪声的鲁棒性。

4 仿真实例

4.1 仿真振动故障信号分离及其效果评价

现有3个模拟滚动轴承故障源信号s1、s2、s3，它们的特征频率和故障类型在表1中给出，信号的信噪比为10 dB。故障源信号经过线性混合模型混合后得到2个观测信号x1、x2(欠定情况)，利用本文提出方法对观测信号进行盲源分离，验证方法的可行性。

表1 模拟的轴承故障特征参数

3个故障源信号的时域和频域特性，如图2所示。图2b中源信号s1的故障特征频率fa与s3的故障特征频率fc以及它们的倍频非常明显;而s2中的滚动体故障特征频率fb及其倍频则由于故障相对微弱和噪声的存在，并不明显。因此，当3个故障信号同时被传感器采集到时，s2会因为另外两个信号以及噪声的干扰而很难被观测到，这极大的增加了故障诊断的难度。

(a) 3个故障的时域信号

2个观测信号的Wigner-Ville分布(WVD)与频谱如图3所示。图3a与图3b中观测信号1的WVD中没有与故障特征频率对应的频带，通过频谱图也不能判断故障是否存在及故障的类型。图3c与图3d中观测信号2的WVD只能看到到较为明显的特征频率fc及其倍频对应的频带，频谱图中也可以观察到fc及其倍频对应的波峰；而另外两个故障的特征频率不能从时频图以及频谱图中观察到。因此，WVD与频谱分析方法仅能确定轴承外圈裂纹故障的存在，而不能判断另外两种故障是否存在。

(a) 观测信号1的WVD (b) 观测信号1的频谱

利用本文提出的基于STFD的滚动轴承多故障欠定盲源分离方法对观测信号进行盲源分离，得到了3个估计源信号，结果如图4所示。

(a) 估计源1的时频图 (b) 估计源1的频谱

图4a中存在明显的故障特征频率fa及其倍频的频带，且没有其他频率的干扰存在；图4b频谱图中存在与故障特征频率对应的波峰，可以判断估计源1是轴承内圈裂纹故障的源信号。同样地，我们可以判断估计源2是轴承滚动体故障的源信号，估计源3是轴承外圈裂纹故障的源信号。由图3与图4可知，本方法可以很好地处理欠定条件下轴承的多故障信号进行盲源分离问题，并对轴承的故障类型进行判断。

4.2 实测的轴承多故障信号分离及其效果评价

4.1节中已经验证了方法的可行性，但是模拟信号通常是基于齿轮箱啮合特性的振动模型，是简化的模型。实际采集信号比模拟信号复杂，它不仅包含齿轮、轴承等关键部件的耦合振动信息，还包含背景噪声及其他干扰信息。因此，有必要通过实验来验证所提出方法的有效性。

本小节将提出的方法应用于轴承多故障信号分离，并进行故障诊断。实验装置如图5所示，图5a为实验台，由变速电机、行星齿轮箱、斜齿轮箱、磁粉制动器和外置轴承座组成；振动加速度传感器分别安装在斜齿轮箱的两侧以及外置轴承座上，如图5b所示。其结构简图和测试故障位置如图6所示。故障轴承在外圈处产生了裂纹故障，如图7所示。故障同时位于斜齿轮箱的输出轴轴承和外置轴承座处。

(a) 实验台

1.磁粉制动器 2.圆柱斜齿轮箱 3.联轴器 4.加速度传感器 5.行星齿轮箱 6.轴承座 7.变速电机 8.外置轴承座

(a) 齿轮箱输出轴轴承外圈裂纹 (b) 轴承座轴承外圈裂纹

实验中电动机转速为2000 r/min，传感器的采样频率为10 240 Hz，采样点数为8192，磁粉制动器施加的扭矩为0。图5b中振动加速度传感器从右到左，采集到的数据依次为源信号1、源信号2、源信号3；行星齿轮箱的减速比为5:1，斜齿轮箱的减速比为1:1.4。表2给出了故障轴承的参数与故障特征频率。

表2 故障轴承参数

3个源信号的时域和频域分析，如图8所示。图8b是3个源信号的傅里叶频谱，源信号1的采集点紧贴轴承座，源信号2的采集点在齿轮箱右侧，距离轴承座较近，所以轴承座轴承外圈裂纹故障的信号更为明显；且由于背景噪声和其他干扰的存在，齿轮箱轴承外圈裂纹故障的信号被淹没了。因此，在傅里叶谱上只能观察较明显的2×f1故障特征频率，其他频率并不明显。源信号3的采集点位于齿轮箱左侧，距离轴承座较远，此时两个轴承的故障特征频率的幅值都很低，并不明显。

(a) 时域信号

接下来对传感器采集到源信号进行时频分析，得到信号的Wigner-Ville分布(WVD)，结果如图9所示。图9a和图9b中只能看到较为明显的2×f1的频带，而特征频率f2几乎看不到，这是因为轴承座轴承外圈裂纹故障信号能量很强，所以能量较低的齿轮箱轴承外圈裂纹故障信号被淹没；图9c中则只能看到在f1和2×f1的两倍频处存在能量集中，但分析效果依旧较差。此外，其他的特征频率的频带不明显，还存在其他无用频带的干扰。因此利用WVD进行时频分析并不能有效地进行故障诊断。

(a) 源信号1的WVD (b) 源信号2的WVD

利用本文提出的方法，对源信号进行盲源分离，得到两个估计的故障信号，结果如图10所示。图10a和图10b中我们可以看到非常明显的故障特征频率f1与2×f1，且在较低频率范围内，不存在故障特征频率f2和它的倍频以及其他频带的干扰，因此我们可以判断估计源信号1是齿轮箱轴承外圈裂纹故障的信号；图10c和图10d中我们可以看到非常明显的故障特征频率f2，且在较低频率范围内，不存在故障特征频率f1和它的倍频以及其他频带的干扰，因此我们可以判断估计源信号2是轴承座轴承外圈裂纹故障的信号。

(a) 估计源1的时频图 (b) 估计源1的频谱

同等情况下，利用Fast-ICA算法对传感器采集到的信号进行盲源分离，得到的结果如图11所示。两个分离出的估计源信号的时频分析与频谱分析中只存在比较明显的2×f1频带与波峰，没有故障特征频率f2的成分。所以Fast-ICA算法并不能对本实验测得的故障信号进行分离与故障诊断。

(a) 估计源1的时频图 (b) 估计源1的频谱

结合图9～图11可知，本文提出的方法可以有效地从实验测得的多故障信号中分离出单个的故障信号，并对故障的类型进行判断。且在同等情况下本方法比Fast-ICA算法的效果要好。

5 结论

本文研究了基于空间-时频分布(STFD)的欠定盲源分离方法，并成功将其应用于滚动轴承多故障振动信号的分离和故障诊断。在本文的研究基础上，得出了以下结论：

(1)本论文提出的方法可以准确的对自动项进行选择与聚类，并重建源信号，能够很好地对混合信号进行分离。

(2)对模拟的多故障信号的盲源分离实验结果验证了本文方法的可行性，能够对多故障信号进行分离与故障诊断。

(3)与Fast-ICA算法相比，在对实测多故障信号进行盲源分离与诊断时，本方法的效果更好。