大断面盾构隧道结构整体化分析方法

何 川， 封 坤

(西南交通大学 交通隧道工程教育部重点实验室， 四川 成都 610031)

0 引言

随着我国综合国力的提升和盾构建造技术的长足进步，一大批涉及公路、铁路、公铁合建以及电力等多个行业的大断面盾构隧道工程大量涌现[1-3]，将盾构隧道建造技术推向了世界前列。目前，我国盾构隧道的建设如火如荼，建造规模越来越大、穿越地层越来越复杂、用途也由单一功能向多功能集约化发展，并已成为越江跨海通道建设的优选工法[4-5]。如文后附表所示，多个工程突破了多项国内甚至世界之最，我国已成为名副其实的盾构隧道建设大国，并正向盾构隧道建设强国稳步迈进。

目前，我国大断面盾构隧道的建设主要呈现出两个趋势，即结构断面大型化和工程条件复杂化。在断面大型化方面，随着公路、铁路、电力等领域运量、运速以及功能集成等要求，断面由中小断面向大断面及特大断面发展，隧道直径由中小直径向大直径、超大直径发展，并正在攻坚特大直径的技术瓶颈，如表1和表2及图1所示。盾构隧道结构断面增大使其使用功能不断丰富,多功能集成成为可能，代表着国际隧道技术发展的新浪潮，也是我国隧道工程发展的必然方向。

我国大断面盾构隧道于21世纪初开始大量出现。在21世纪前10年，大断面盾构隧道以直径10～12 m最为常见，如武汉长江隧道(双向4车道，外直径11.0 m)、广深港狮子洋隧道(双洞双线，外直径10.8 m)以及庆春路隧道(双向4车道，外直径11.3 m)等。近10年来，盾构隧道建设正向14～17 m超大直径快速发展，超大直径隧道工程不断涌现，如三阳路长江隧道(双向6车道+双线地铁，外直径15.2 m)、江阴靖江长江隧道(双向6车道，外直径15.5 m)。

表1 盾构隧道断面划分标准

表2 盾构隧道直径划分标准

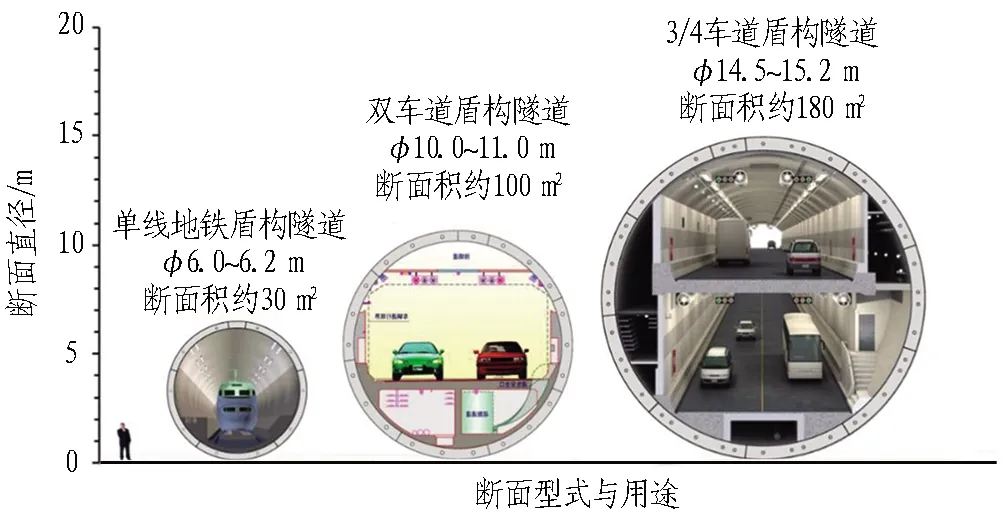
图1 盾构隧道断面大小及断面形式发展过程

回顾隧道断面的发展，从中小直径到大直径再到超大直径，10年一个跨越，不断刷新纪录、突破技术瓶颈。当前，我国15 m级超大直径的建造技术基本成熟，正在进行18 m级特大直径盾构隧道的技术探索。拟建的深圳机荷高速荷坳隧道(高速公路，单洞双层6车道，外直径可达17.5 m)，可望超过美国Alaskan Way SR99公路隧道，成为世界最大直径的盾构隧道。

另一方面，我国幅员辽阔，地质条件区域性特征明显、差异巨大，东有以上海、杭州等地区为代表的软土地层，南有以广州、深圳为代表的复杂红层，北京、南京、成都等多地富水砂卵石、卵砾石地层发育，并不断遭遇岩溶、断层、膨胀岩/土、黄土等不良地质，工程建设条件区域性差异十分显著[6]。

早期盾构隧道工程主要修筑于匀质软土地层，而随着断面增大隧道埋深也大幅增加，如广州、深圳等地新建的公路、铁路隧道，埋深最大处已近100 m；现今大量规划的城市排水深隧，规划深度为50～80 m；我国多条采煤、输油/气隧道，埋深近千米。由于埋深较大，这些盾构隧道多处于风化岩层，并大量穿越复杂地层、不断遭遇不良地质，主要表现有地层由“单一”变“复合”、由“软”变“硬”，水压由低变高，如： 武汉三阳路隧道、南京和燕路隧道大段穿越土岩复合地层，并遭遇多条断层、岩溶，最高水压超过0.6 MPa；佛莞狮子洋隧道，全断面泥岩占比超过80%，穿越多条断层，最高水压接近0.7 MPa；珠三角城际铁路广佛环线东环隧道，穿越炭质板岩、砂岩、灰岩等复杂岩层，最大埋深超过120 m，最高水压接近1.2 MPa。随着我国盾构隧道建设进一步向特大、超深发展，工程建设条件必将更加复杂。

正是由于地质条件、环境条件的复杂性与差异性，现行经典计算理论与方法在对于大断面盾构隧道的分析中存在差异性，适应性较差，与蓬勃发展建设的大断面盾构隧道工程相比，其计算分析理论常常滞后于工程实践。特别是盾构隧道管片结构分析，仍以20世纪末德国、日本等国提出的计算理论和分析模型为主[7]，限于当时盾构技术水平，上述方法的形成主要依据中小直径盾构隧道的工程设计经验，而在大直径、超大甚至特大直径盾构隧道结构的分析中存在适应性问题[8]。

有鉴于此，作者结合多年来针对大/超大断面盾构隧道管片结构分析研究的实践与经验，总结提出可充分考虑大断面盾构隧道结构特征的整体化分析方法，并通过模型、足尺、原型、现场等系列试验，验证该方法对于大/特大断面、高水压、复杂地层等特殊条件的适用性，可为复杂条件下大/特大断面盾构隧道结构的高精度分析与合理化设计提供参考。

1 大断面盾构隧道的结构特征

大断面盾构隧道结构管片接缝面构造复杂，管片大体积效应显著，衬砌结构纵-横向空间效应突出，受水压与地层影响敏感，施工期结构体系脆弱，其结构特征主要包括以下方面。

1.1 管片接缝构造复杂

大断面隧道管片尺寸较大，螺栓常采用易拆卸的斜螺栓型式。为了保证拼装精度，通常采用凹凸榫槽或剪力销以便于拼装定位；为了提高管片接头传力性能，接缝面常设有传力衬垫；此外，由于常采用双道防水，导致管片接缝面的细部构造复杂。大断面盾构隧道接头细部构造如图2所示。在高水压、大埋深等高围压作用下，管片结构的接头刚度受高轴压影响，不连续接触面的变形过程与传力性能更为复杂，非线性特征显著，现有中小直径盾构隧道的接头刚度参数与计算方法不适用，需深入研究，准确求解大/特大断面盾构隧道的接头刚度与变形性能[9]。

(a) 管片接头 (b) 接缝面构成

同时，管片结构断面增大，管片环分块数量将随之增加。管片分块形式随断面直径的变化如图3所示。可以看出： 接头数量增多，一方面令管片结构整体刚度降低；另一方面，接头的抗弯性能与压弯变形对整体管片结构的受力状态与变形规律的影响程度更显著，因此，大断面盾构隧道管片结构分析对管片接头的力学参数更为敏感[10-11]。

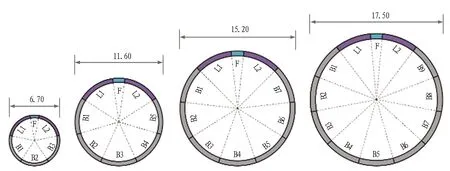
(a) “3+2+1”分块 (b) “5+2+1”分块(c) “7+2+1”分块 (d) “9+2+1”分块

1.2 管片结构空间效应明显

随着管片结构断面增大，管片衬砌的设计也趋向于厚型化、宽幅化，与以城市地铁为代表的中小直径盾构隧道相比，管片厚径比有所降低。通常，中小直径盾构隧道(外径4～8 m)管片厚度一般为0.3～0.5 m，管片厚径比往往大于0.06，幅宽相对较小(一般为1.0～1.5 m);而大断面盾构隧道管片厚径比一般小于0.05，接近0.04。盾构隧道管片厚径比随断面直径的变化如图4所示。可以看出： 1)直径增大导致管片相对刚度减小，稳定性降低，外界荷载与地层抗力变化引起的结构响应加剧； 2)管片结构横向与纵向变形相互影响更显著，结构内力与变形均体现出空间分布特征，传统计算方法无法准确表征地层-结构相互作用与结构空间效应。

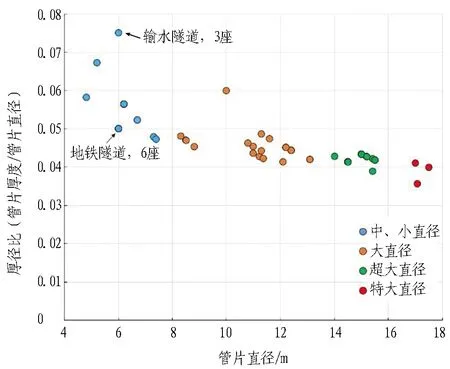
图4 盾构隧道管片厚径比随断面直径的变化

1.3 复杂地层影响敏感

复杂地层条件下盾构隧道管片结构与围岩的相互作用更为复杂，在管片脱环受荷的过程中，土层、岩层的作用方式有差异，加上地下水的影响，导致围岩-管片衬砌间的相互作用将发生明显变化，使围岩荷载、抗力及二者对管片的约束作用复杂化，该差异如何在计算模型中准确表征值得讨论；同时，由于断面较大，同步注浆分布形态、充填程度与浆液强度的形成更易受地层、地下水等因素影响，现有计算模型和方法很难适应这一变化。

另一方面，当隧道穿越软硬不均、地层刚度突变等地层和跨越断层等复杂地质时，大断面管片结构纵-横向耦合作用效应突出，如仍采用传统分析方法，将横、纵向结构割裂分析，往往难以反映荷载的空间分布变化、结构-横向耦合作用以及围岩-结构相互作用的空间差异。

1.4 施工荷载成为重要控制因素

隧道增大、埋深加大，导致盾构推力、转矩、注浆压力等均大幅增加，而大断面盾构隧道管片分块多，施工期结构体系相对脆弱，在管片拼装、顶推、注浆等过程中，可能造成管片开裂、破损(见图5)，需结合不同阶段施工荷载及管片衬砌的拼装状态进行分析。该分析模型与计算同样需符合管片纵-横向连接的结构特征，并体现施工期荷载的空间分布条件。

(a) 纵向裂缝

(b) 管片掉角

综上，大断面盾构隧道为地下不连续多体空间结构，精准的结构分析是进行结构安全设计与控制的前提。鉴于此，整体化分析方法需从接头刚度获取、计算模型建立、刚度迭代计算、衬砌结构-地层相互作用表征等方面出发，通过模型、足尺、原型、现场等系列试验修正与校验，以实现对复杂结构和特殊条件的高精度分析。

2 大断面盾构隧道结构整体化分析方法的要点

对于大断面及特大断面盾构隧道，管片接缝构造复杂，管片大体积效应显著，衬砌结构纵-横向空间效应突出，受水压与复杂地层影响敏感，施工期结构体系脆弱，部分隧道还需设置内衬或局部内衬，应采用更为精细分析方法才能实现对结构内力和变形的准确计算。

鉴于以上原因，从大型盾构隧道多体拼装结构的特征出发，提出了盾构隧道结构整体化分析方法。盾构隧道整体化分析方法框架如图6所示。其具体思路如下： 1)从细部着手，通过理论分析、数值模拟、足尺试验等手段获取盾构隧道接头非线性力学特征与参数，以此为基础建立基于厚壳或实体的三维分析模型； 2)考虑复杂地层荷载、内外水压以及施工荷载等与衬砌结构的交互作用，通过迭代计算法求解管片结构整体受力，该方法可准确体现高水压、多体接触、注浆层影响等效应，实现对大/特大断面盾构隧道结构内力和变形的精确求解； 3)通过大量从模型到原型级别的试验研究、现场实测等手段对整体及局部力学行为、破坏特征以及计算模型进行验证与优化。

图6 盾构隧道整体化分析方法框架图

目前，整体化分析方法已在我国大断面盾构隧道的结构设计中获得大量应用，其要点是准确获取局部参数，正确表征整体结构，精确体现交互作用。具体体现在如下方面：

1)准确获取管片接缝面的接头刚度。因大断面隧道的接头刚度受接缝面构造影响极大，具有受轴力和弯矩同时影响的双参量非线性特性，可采取原型加载试验或数值分析获得。

2)建立准确反映管片环及复合衬砌特征的三维分析模型，并适应单层管片以及设置内衬或局部内衬的分析需要，可采用壳-弹簧-接触等分析模型。

3)结构分析的求解方法要体现结构-地层(地下水)交互作用以及接头的非线性特性，可采用迭代分析等方法实现。

4)荷载体系要充分考虑运营与施工阶段荷载的演变特征，分析得出准确的控制性荷载。

3 大断面盾构隧道结构整体化分析方法的技术内容

3.1 大断面盾构隧道接头双参量非线性刚度

大断面盾构隧道管片接头是由具有复杂构造的接缝面和螺栓等组成的三维复杂结构，其力学功能主要为实现管片连接并传递载荷。在进行盾构隧道管片结构分析时，通常将接头等效为若干可发生转动变形的弹簧，弹簧的转动刚度即为接头的抗弯刚度，其取值对于计算结果具有较大的影响。研究表明，管片接头抗弯刚度主要与接头构造参数等相关，并受接缝处的受荷条件控制。现阶段管片结构设计中，常常采用类比法(即类比隧道直径相仿或厚度相同的管片接头)确定接头抗弯刚度，往往造成较大的误差。因此，获取大断面盾构隧道管片接头的抗弯刚度是实现管片结构高精度分析的前提。

3.1.1 接头双参量抗弯力学特性

为求解大断面盾构隧道接头抗弯刚度，探明其抗弯性能，课题组从接头局部出发，针对管片接头开展了精细化数值仿真，并结合接头足尺试验对接头抗弯性能进行了系统校验。

相较其他手段，数值仿真是容易开展的有效手段。为便于计算，在既有的研究中建立接头模型时常常忽视接头构造特征的复杂性[12-14]，导致计算结果失真。大断面盾构隧道接缝面构造和接缝面接触关系对于接头抗弯性能的计算结果有较大影响，因此计算模型中应尽量真实地进行还原[15]，宜包括混凝土管片、螺栓、垫片和套筒等结构元素，并准确描述这些元素的接触作用关系。

大断面盾构隧道管片接头常采用多颗螺栓连接，如图7(a)所示，由于接头处荷载沿幅宽一般为均匀分布，因此可选取1/m幅宽的宽度(m为螺栓沿幅宽布置的数量)，并采用单颗螺栓等效代替全幅宽管片接头计算，可节省大量计算资源。另外，因大断面盾构隧道管片接头处曲率较小，可“以直代曲”，从而使接缝面处在变形过程中始终处于纯压弯状态，从而保证抗弯刚度不受接缝面赘余力干扰，如图7(b)所示。

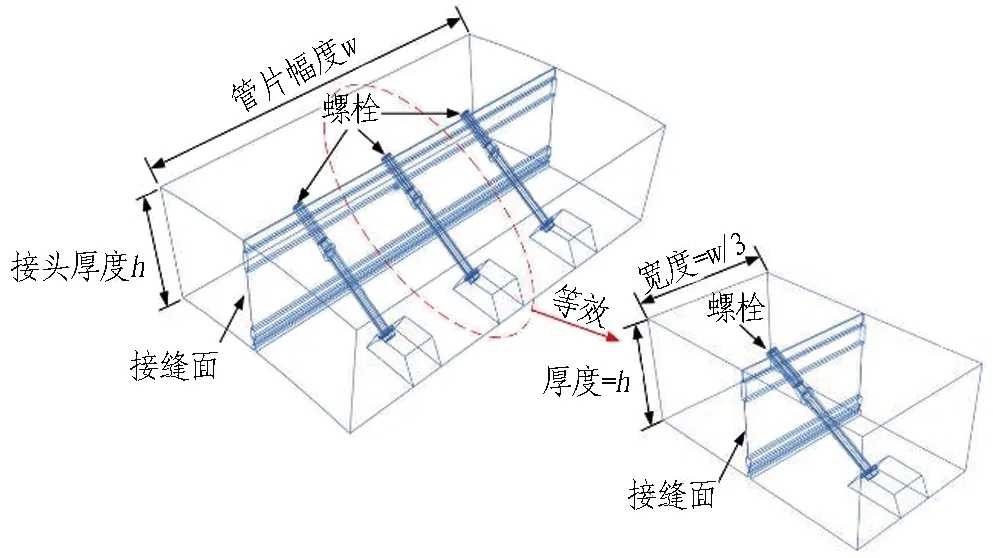
(a) 模型等效

(b) 模型建立

抗弯试验是获取接头刚度最直接的方法[16-19]，试验的关键在于保证接头处于纯压弯受力状态，否则接头处将产生赘余力，导致试验结果偏差。鉴于此，课题组近年来陆续研发了可模拟接头受力状态与边界条件的接头抗弯试验装置(水平和竖向最大加载能力均为5 000 kN)，如图8(a)和8(b)所示，并针对南京长江隧道、广深港狮子洋隧道、苏通GIL综合管廊隧道以及江阴靖江长江隧道等国内重大隧道工程开展接头抗弯试验[20-22]，如图8(c)所示。

(a) 正视图(单位： mm)

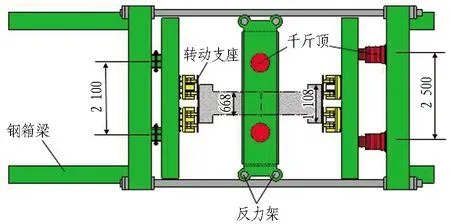
(b) 俯视图(单位： mm)

(c) 接头抗弯足尺试验实况

从试验与计算的结果发现，接头抗弯性能同时受接头所受轴力和弯矩2个参量控制，接头的抗弯刚度呈明显的非线性变化。接头弯矩-轴力-张开角三维曲面(以高铁狮子洋隧道工程管片接头为例)如图9所示。接头刚度随轴力和弯矩的变化而动态变化，接缝面张角变化较小时接头抗弯刚度相对较大，而当接缝面张角大于0.005 rad后，接头抗弯性能随弯矩增大逐步衰减，正弯与负弯作用下接头刚度及其变化规律不同，轴力的增加对接头抗弯性能的保持有益。

图9 接头弯矩-轴力-张开角三维曲面(以高铁狮子洋隧道工程管片接头为例)

3.1.2 理论计算模型

大断面盾构隧道接头型式多样，接缝面构造型式、尺寸多样，工程中在进行接头刚度求解时往往“一隧一算”，耗费大量人力物力。采用理论计算模型是极为有效的解决途径，但传统理论计算模型针对中小直径盾构隧道建立适用性不强，主要受如下2方面因素影响。

1)大断面盾构隧道接头接缝面构造复杂，高轴压作用下混凝土、螺栓、传力衬垫等材料非线性特征明显，传统模型不能计入。

2)接缝面变形为曲面，传统模型将接缝面变形简化为平面，无法体现接缝面几何非线性变化。

基于试验现象对压弯作用下管片接头变形过程进行剖析，建立了大断面盾构隧道复杂接缝面管片接头抗弯力学模型[23]，如图10所示。该模型可计入接缝面细部构造(见图10(a))、混凝土及传力衬垫的非线性力学特性、接缝面荷载传递特性以及接头螺栓预紧作用的影响，能够表征管片接缝面混凝土开裂与压碎、螺栓屈服以及接头破坏，并采用2段平面描述接缝面张开变形，实现了对接缝面非线性变形的刻画。

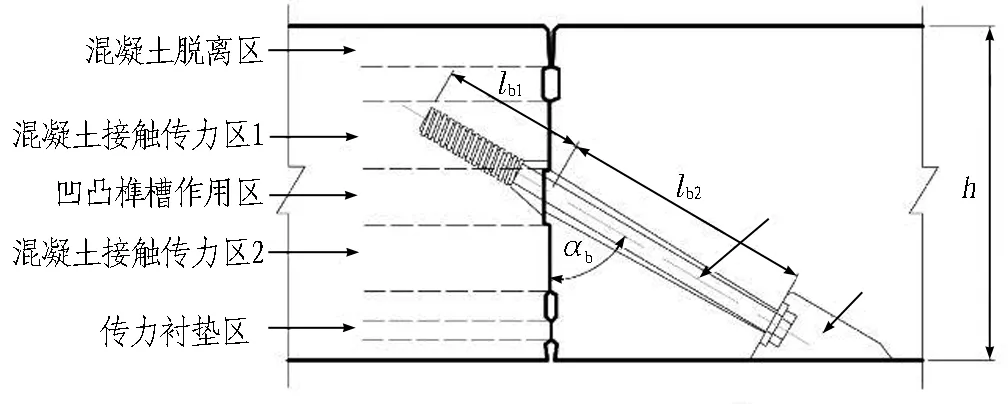
lb1为螺栓锚固端到接缝面的长度；lb2为螺栓非锚固端到接缝面的距离；αb为螺栓与接缝面的夹角；h为接缝面厚度。

(a) 接缝面功能分区图

M为接头弯矩;N为接头轴力;h1为AB段长度；h2为AD段长度；h3为AE段长度；hb为AF段长度(F为螺栓作用点与接缝面的交点)；hoc为A点到接缝面中心的距离；Fc、FG为DE段和AB段混凝土应力分布函数；Tb为单颗螺栓的拉力；n为螺栓个数。

(b) 抗弯力学模型

图10 复杂接缝面管片接头抗弯力学模型

Fig. 10 Bending mechanical model of segmental joint with complex joint surface

采用该理论模型对广深港狮子洋隧道和南京长江隧道管片接头抗弯性能进行分析，并与试验结果进行对比，验证了该力学模型的可靠性。复杂接缝面接头力学模型与足尺试验结果对比如图11所示。

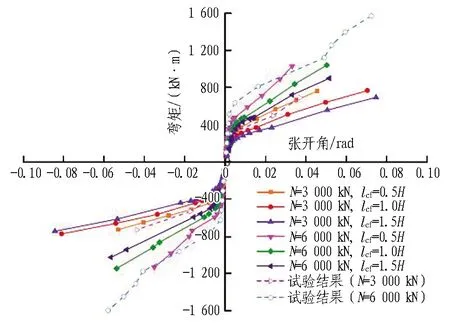
(a) 狮子洋隧道-凹凸榫槽型接头

(b) 南京长江隧道-平板型接头

lef为受压区外边缘压应变的影响深度；N为接头轴力；H为接头厚度。

图11 复杂接缝面接头力学模型与足尺试验结果对比

Fig. 11 Comparison between analytical model and full-scale tests

3.1.3 接头双参量抗弯刚度

进一步地，考虑到既有抗弯刚度计算方法的复杂性，基于前述获得的接头抗弯刚度双参量变化特征，依据不同直径盾构隧道试验与研究结果，提出了便于工程应用的接头抗弯刚度的谱系值。盾构隧道接头抗弯刚度谱系值如表3所示。

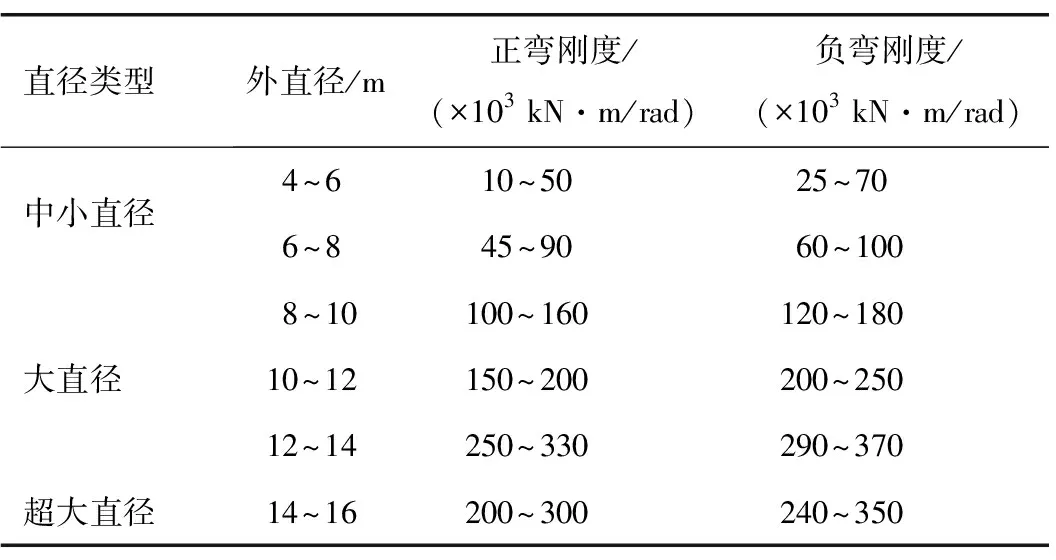
表3 盾构隧道接头抗弯刚度谱系值(中位值)

同时，对典型大断面隧道工程管片接头抗弯性能进行分析，发现接头构造特征是影响接缝面接触作用关系的重要因素，而止水措施、凹凸榫构造易造成接缝面接触变形不连续，从而使接头刚度呈分段变化。大断面盾构隧道接头止水构造型式示意如图12所示。大断面盾构隧道接头抗弯刚度计算公式与试验结果对比如图13所示。基于该特质，分别针对双侧设置止水构造和单侧设置止水构造的接头，提出了大断面盾构隧道接头抗弯刚度的简明计算公式。

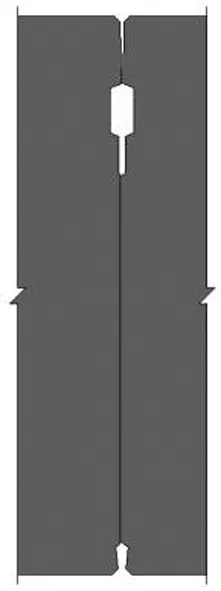
(a) 仅设外侧止水构造

(b) 设双侧止水构造

(a) 正弯弯矩-转角关系

(b) 负弯弯矩-转角关系

1)对于双侧设置止水构造的接头，其正负弯矩下的弯矩-转角曲线宜采用3分段函数表达，如式(1)所示。

(1)

2)对于仅外侧设置止水构造的接头，其正弯刚度呈3段曲线变化，可采用式(1)表示；而负弯矩-转角曲线一般分为2段，可统一用式(2)表示。

(2)

式(1)—(2)中：M为接头弯矩，kN·m；N为接头轴力，kN；θ为接头转角，rad；a1—a9为接头厚度h和混凝土弹性模量E的参数；θ1=k1N，为接头开始发生张开变形；θ2=k2N+k3，为接缝面外缘混凝土接触时的接头转角；k1—k3为常数。

式(1)和式(2)简明计算式可在保证一定计算精度的前提下定量描述接头刚度的非线性变化特征，准确反映接头压弯分阶段变形过程，同时便于工程采用。

3.2 大断面盾构隧道结构多体分析模型

目前，我国在进行盾构隧道管片衬砌受力分析时常采用的模型有匀质圆环模型、全铰圆环模型、梁-弹簧模型和梁-接头不连续模型等，这些模型均采用“梁”来表征管片，不能体现结构断面增大引起的变形与内力在幅宽方向上的分布变化；同时，不能描述复杂地层中围岩、注浆层与管片结构相互作用在空间上的变化与影响。

盾构隧道管片结构主要由管片、连接螺栓通过错缝或通缝的方式拼装而成，其拼装成环后内力的形成过程主要与管片结构、围岩、地下水、注浆层等的交互作用相关。精细化的计算模型在考虑准确描述管片衬砌接头的连接与传力关系的同时，还需精确反映围岩、注浆层与衬砌结构的相互作用，并计入地下水对衬砌结构的影响。因此，采用壳体或实体描述管片，并实现围岩、地下水、注浆层等多体相互作用的精确刻画，是实现大断面盾构隧道管片结构高精度分析的基础。

3.2.1 壳-弹簧-接触模型

基于管片结构受力的空间效应，国内学者提出了平板壳-弹性铰-地基系统模型和壳-弹簧模型，这2种模型将带接头的管片衬砌内力分析拓展到了三维壳体结构，但计算仍采用荷载-结构模式，即施加主动荷载和采用Winkler弹性地基理论考虑被动抗力，不能准确反映围岩-衬砌的相互作用。鉴于此，基于有限元方法，建立了地层-结构模式下的壳-弹簧-接触计算模型[24]。该模型采用厚壳单元表征了大断面管片结构的空间受力特征，可导入接头刚度体现管片接缝处的挤压、弯曲与剪切作用，更重要的是采用接触关系描述了管片与围岩的相互作用。地层-结构模式下的壳-弹簧-接触模型如图14所示。

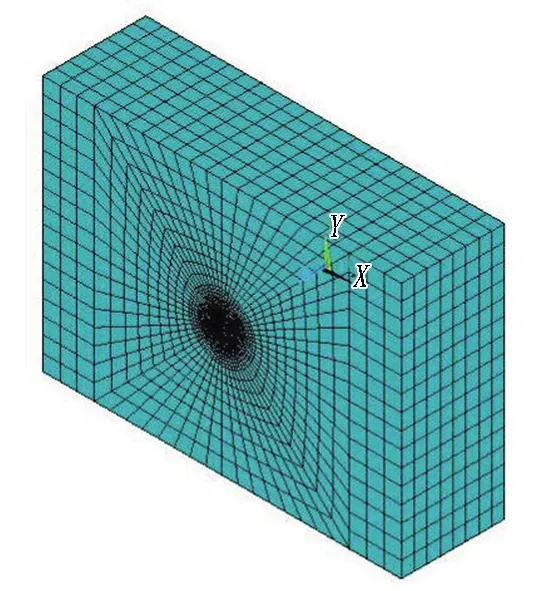
(a) 整体模型

(b) 管片结构模型

3.2.2 二次衬砌模型

对于敷设二次衬砌的大断面盾构隧道，管片与二次衬砌结合面层间接触作用关系是影响分析结果的关键，通常按层间连接强度或连接状态可分为2种，即复合结构和叠合结构，区别在于层间是否传递剪切力。对于复合结构，层间光滑(未做凿毛处理或植筋接驳)，认为其层间只传递压力，不传递剪切力；而叠合结构层间具有较强的黏结力和摩擦力，可以充分传递剪力作用，可按库仑摩擦考虑。基于以上假定，考虑双层衬砌中管片衬砌环内与环间接头、管片与二次衬砌间的压缩与剪切关系、二次衬砌纵向的搭接关系等，建立敷设二次衬砌双层衬砌的概化模型，如图15所示。

图15 敷设二次衬砌双层衬砌的概化计算模型

对于叠合式与复合式2种模式，可采用接触或层间弹簧描述，如采用弹簧(见图16)，可据式(3)—(5)计算层间压缩刚度[25]。

叠合式：

(3)

复合式：

(4)

其中：

(5)

式中：KY为双层衬砌层间压缩总刚度，kN/m；KY1、KY2为管片和二次衬砌压缩区单元的压缩刚度，kN/m；E1、E2为管片和二次衬砌混凝土的弹性模量，kN/m2；t1、t2为管片和二次衬砌的厚度，m；AY为压缩区域内的截面面积，m2；KY3为内外衬中间夹层单元的压缩刚度，kN/m；E3为内外衬弹性模量，kN/m2；t3为内外衬中间夹层单元的厚度，m。

(a) 叠合式

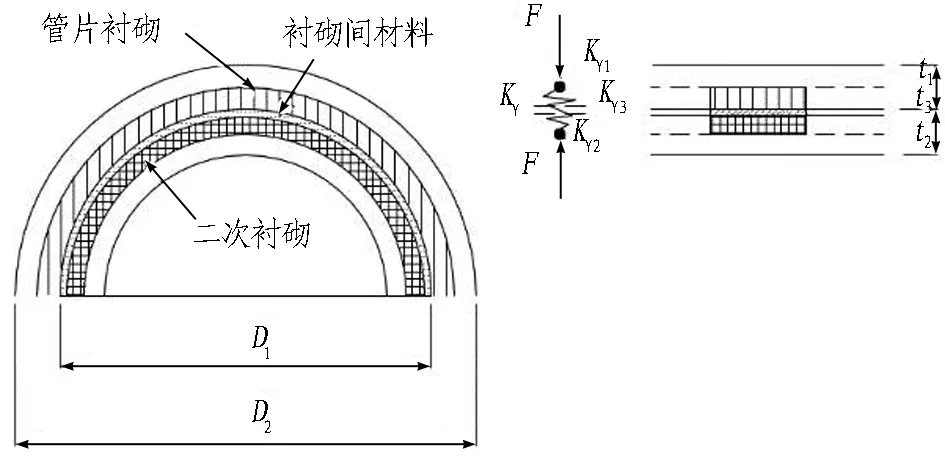
(b) 复合式

3.2.3 注浆层/地层作用效应

盾构隧道壁后填充层对于隧道结构受力影响较大，大断面盾构隧道通常采用同步注浆方式充填盾尾空隙。对于地下水发育或富含有害离子的区段，浆液材料易受地下水冲蚀及有害离子作用，造成长期强度损失。以水泥-水玻璃双液浆为例，该材料目前多用于地下水发育区段注浆堵水、壁后充填。由于与地下水反应产物不稳定，形成的反应产物部分被地下水冲蚀剥离，形成蜂窝状注浆体。双液浆反应产物分布与随机有限元模型如图17所示。

(a) 剖面显微镜图像

(b) 数值模型剖面

针对水泥-水玻璃双液浆的耐久性问题，提出了基于细观结构观测的长期性能评价方法[26]，通过细观观测对双液浆反应产物进行空间分布特性识别，据此采用随机有限元方法建立双液浆试件劣化模型，获得水泥-水玻璃双液浆反应产物的力学性能的折减参数，可对注浆层的劣化状态进行精确描述。

3.3 基于接头刚度的管片结构迭代算法

盾构隧道衬砌结构的精准分析，是再现围岩-结构-地下水交互作用的数值过程，其中，管片衬砌的接头刚度随荷载作用、约束关系、变形状态等影响是一个动态的过程，反观之，围岩压力的作用与变化也与管片衬砌的刚度变化、变形状态息息相关，其中关键的控制参数是接头的双参量抗弯刚度。

由上述分析可知，管片接头的真实抗弯刚度并不是定值，其取值反映了外部围岩压力、水压力的作用，受接头处轴力和弯矩状态控制，同时又反过来影响整体刚度与局部受力。因此，在分析模型中，不同位置处管片接头受内力控制，其抗弯刚度取值不同，分析过程不宜将接头抗弯刚度设为常数，需逐步迭代以逼近真实值。实现接头刚度迭代，准确反映围岩、地下水等交互作用，是实现大断面盾构隧道管片结构高精度分析的关键。

为了保证模型计算结果的准确性，提出了接头刚度迭代算法[27]，其基本原理如下： 将每一个接头刚度和内力视为未知数组合(ki,Mi,Ni)，计算模型可视为接头内力关于接头刚度的函数(Mi,Ni)=f(ki)，而根据接头抗弯性能分析所得的抗弯刚度与接头内力关系式或三维曲面可视为接头抗弯刚度关于接头内力的函数ki=g(Mi,Ni)；当接头个数为x时，模型中未知数个数为3x，而方程数为2x，因此将接头抗弯刚度作为变量进行迭代分析，其迭代计算过程如图18所示，其要点如下：

1)定义整环计算模型中x个接头单元的初始抗弯刚度为kθ1，代入计算模型进行求解，提取x个接缝处的管片衬砌的结构内力(弯矩M1、轴力N1)。

2)将结构内力弯矩M1、轴力N1代入接头抗弯刚度的三维曲面关系，利用加权内插法求解接头抗弯刚度kθ2。

3)将x个接头抗弯刚度kθ2重新代入模型进行计算，求解结构内力，以此循环。

4)比较第i步计算的kθi和第i+1步计算的kθi+1，如果2次计算的接头刚度无限逼近，则退出循环，此时的接头刚度即为结构所受外力作用下的真实抗弯刚度，以此刚度计算所得的结构内力也是准确的。

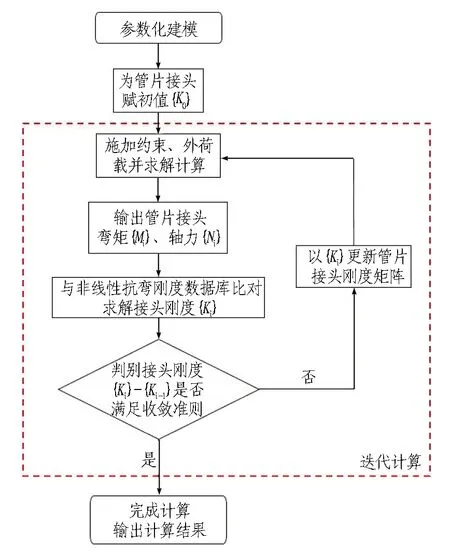
图18 基于接头刚度的管片结构迭代算法流程图

以高铁狮子洋隧道为例，采用该算法对考虑和不考虑接头刚度迭代时管片结构内力及位移的变化情况进行分析。不同迭代次数下的结果比较如图19所示。

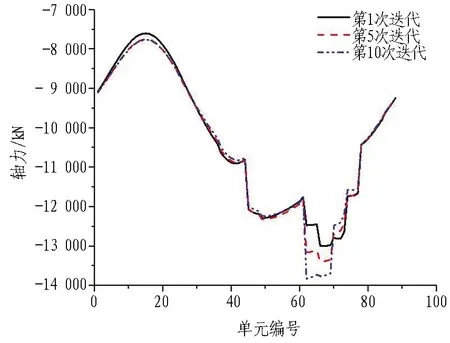
(a) 轴力变化

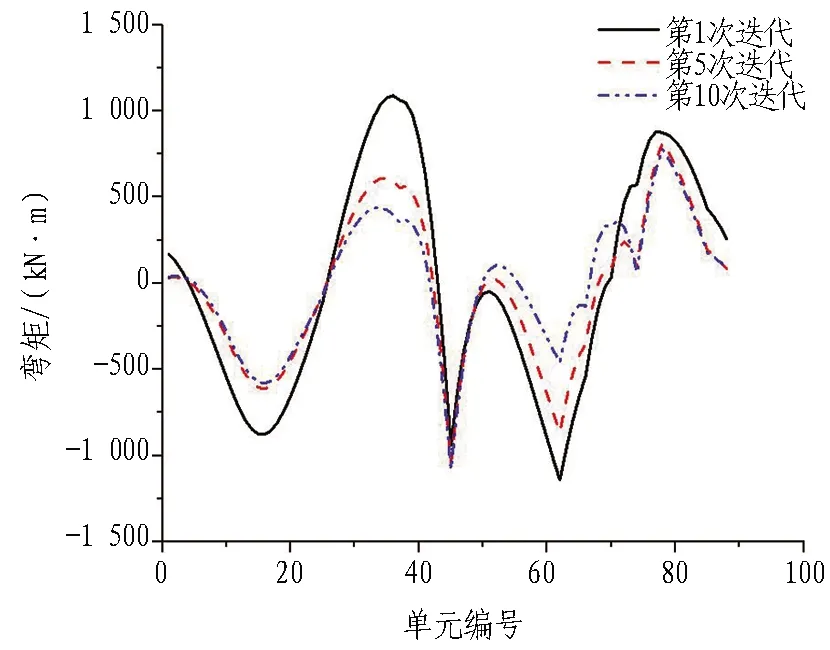
(b) 弯矩变化

(c) 位移变化

(d) 接头刚度

由图19可知： 1)在不同刚度迭代次数时，接头刚度迭代对管片结构上弯矩分布形态影响不大，但对不同位置处内力与变形量值的影响较大； 2)采用迭代算法后，计算结果将随迭代过程逐步逼近真值。

进一步地，针对多座大及特大断面盾构隧道管片结构开展相似模型试验[9, 28]和原型加载试验[29-32]对该迭代计算结果进行对比验证。大断面盾构隧道管片结构原型试验(以高铁狮子洋隧道为例)如图20所示。

(a) 相似模型试验

(b) 原型管片加载试验

以水压60 m、土压35 m的试验工况为例进行分析，分别将轴力、弯矩和位移的原型试验结果与相同荷载模式下的壳-弹簧模型和考虑接头抗弯刚度迭代的壳-弹簧模型计算结果进行对比，如图21所示。其中，考虑接头刚度迭代与不考虑接头刚度迭代的接头抗弯刚度初始值相同，均为150 MN·m/rad。

(a) 轴力对比

(b) 弯矩对比

由图21可知： 1)考虑接头刚度迭代后，计算结果与传统壳-弹簧模型的计算结果具有一定的差异，特别是管片结构位移的差异相对较大； 2)无论是结构轴力、弯矩还是位移，考虑接头刚度迭代后的计算结果均相较于不考虑接头刚度迭代的计算结果更加接近试验值，可见接头刚度迭代算法具有更高的计算精度。

3.4 施工期分阶段分析

大断面盾构隧道管片衬砌由于分块较多、结构体系复杂，在管片拼装、脱环顶推、壁后注浆、后期稳定等4个施工阶段，管片结构的安全性常常面临极大威胁。针对施工期这4个阶段开展结构分析，不仅可预判结构风险、有效避免管片破损与渗漏、防止隧道失稳垮塌，还能获取运营期管片结构分析的初始应力与变形条件，使大断面盾构隧道结构分析更为完备。

盾构隧道管片结构在不同施工阶段的边界条件、荷载条件差异较大，需对不同阶段分别进行分析。针对盾构隧道施工期管片拼装、脱环顶推、壁后注浆、后期稳定等阶段提出了施工期盾构隧道结构分析与稳定性控制方法，可采用分阶段分析建立相应模型进行各阶段结构受力分析。盾构隧道施工期分阶段分析如图22所示。盾构隧道施工期各阶段要素如表4所示。

图22 盾构隧道施工期分阶段分析

表4 盾构隧道施工期分阶段分析要素

以管片拼装过程的力学响应分析为例，在管片拼装过程中，位于盾尾的管片将承受千斤顶推力、油脂压力、螺栓预紧力、管片自重、结构间(管片与管片、管片与盾尾刷)相互作用力以及由于环面不平整或拼装误差导致的装配力等施工荷载。根据拼装过程中管片的约束条件或接触条件将其分为两侧无约束、单侧受相邻块约束、两侧受相邻块约束3类，提出了拼装阶段拼装环管片的3类受力模式[33](见图23)，并据此建立了管片拼装过程的三维数值模型(见图24)。

结合佛莞城际铁路狮子洋盾构隧道全断面岩层段的现场实测数据，对比分析了管片拼装过程的环向内力响应规律，如图25—27所示，发现了全断面岩层段管片拼装过程引起的内力响应显著，管片处于“弯矩大轴力小”不利受力状态的现象，也验证了计算模型的可靠性。

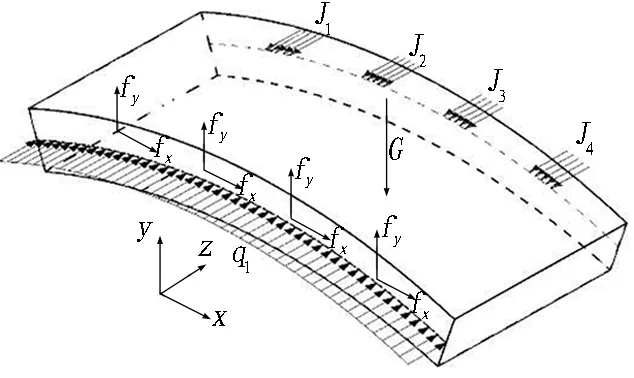
(a) 两侧无约束

(b) 单侧受相邻块约束

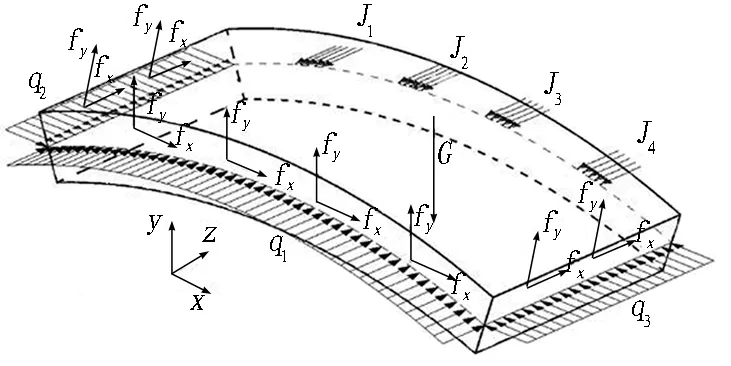
(c) 两侧受相邻块约束

(a) 拼装环管片模型

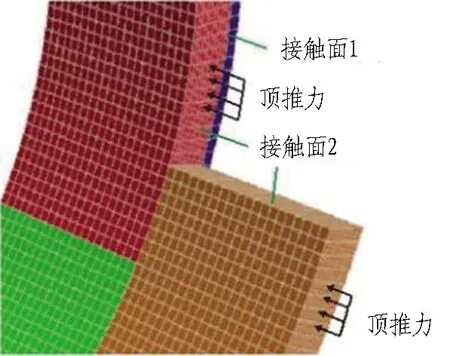
(b) 模型细部情况

(a) 盾尾管片拼装过程示意 (b) 监测环拼装顺序 (c) 拼装过程测试

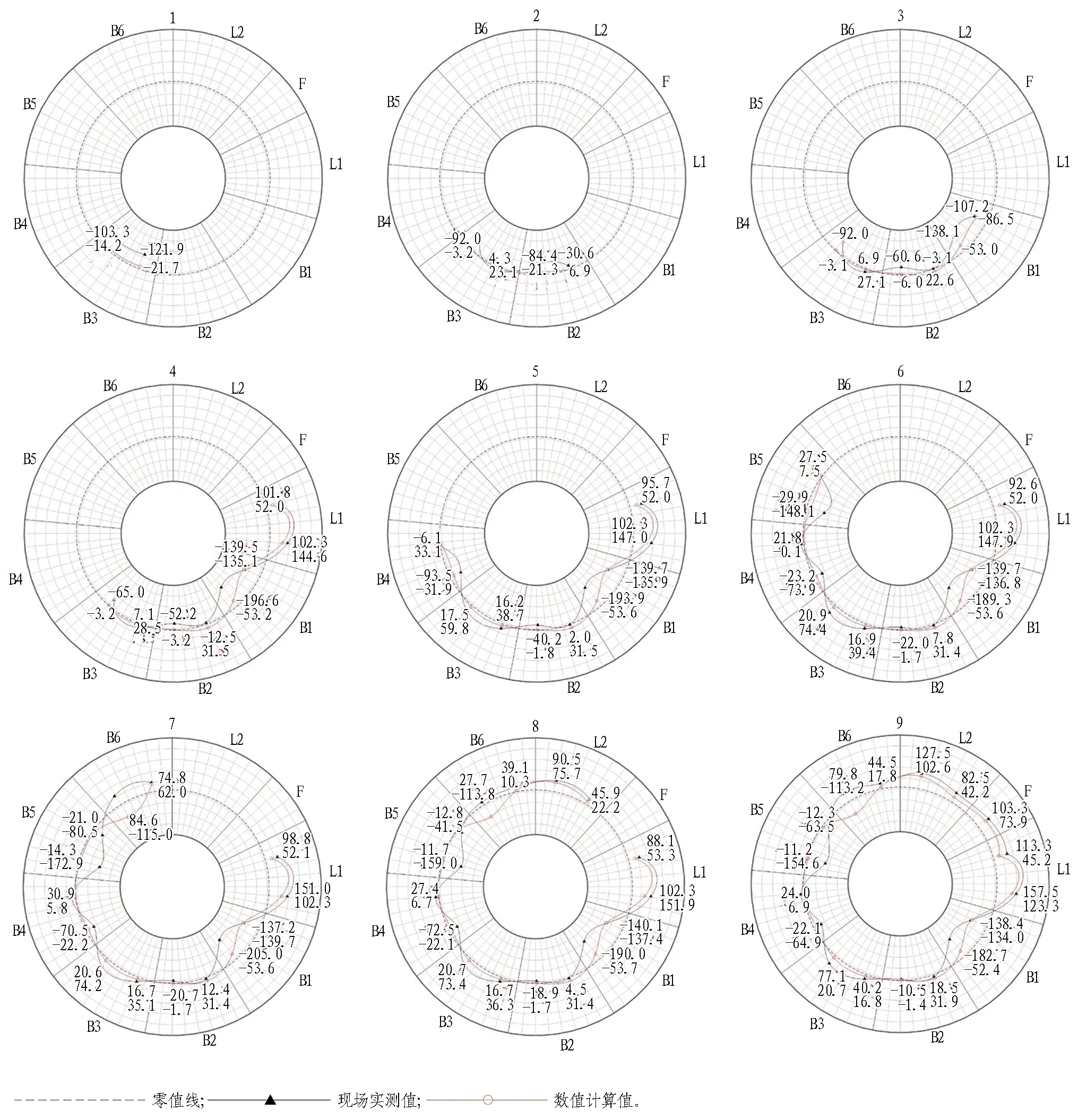
图26 拼装阶段管片弯矩变化过程图(单位： kN·m)

图27 拼装阶段管片轴力变化过程图(单位： kN)

4 结论与展望

针对大断面盾构隧道的结构特征，提出了准确获取局部参数、正确表征整体结构、精确体现交互作用的整体化分析要点，建立了适用于大/特大断面盾构隧道的整体化分析方法，经模型、足尺、原型、现场等多层次的试验验证，该方法可准确体现高水压、多体接触、注浆层劣化等效应，可实现对大/特大断面盾构隧道结构的高精度分析。盾构隧道结构整体化分析方法已纳入国家标准GB/ T 51438—2021《盾构隧道工程设计标准》，该标准明确要求： 对大断面及超大断面、构造型式复杂的隧道，或承受大偏压、高水压、严重形变压力等条件下的特殊隧道，应采用整体化的分析方法进行衬砌结构的内力和变形计算。主要结论如下：

1)准确获取管片接头的抗弯刚度是大断面盾构隧道结构整体化分析的前提。针对管片接头抗弯刚度双参量非线性变化特征提出了适用于大/特大断面盾构隧道的管片接头抗弯刚度的谱系值和计算公式。

2)精确刻画围岩、地下水、注浆层等多体相互作用，是实现大断面盾构隧道结构整体化分析的基础。通过建立壳-弹簧-接触模型，引入二次衬砌与管片的层间相互作用，计入注浆层劣化的影响，可精确表征大断面盾构隧道结构的空间效应，反映地层-结构的相互作用。

3)实现接头刚度迭代是大断面盾构隧道结构整体化分析的关键。通过接头刚度的动态迭代更新，可准确体现结构-地层-地下水交互作用，使计算结果具有更高的精度。

4)精准解析施工期荷载的演变过程与结构的受荷特征是大断面盾构隧道结构整体化分析的要素。通过描述施工期管片拼装、脱环顶推、壁后注浆、后期稳定等主要施工阶段的荷载演变与结构特征，可预判结构风险,有效避免管片破损与渗漏，防止隧道失稳垮塌。

下一步，将继续针对全生命周期围岩与衬砌的劣化指标与性能演化规律开展研究，不断深化与完善整体化分析方法,加强应用实践，为我国大型及复杂盾构隧道结构的性能分析与服役安全评价提供有力支撑。