面向人机协作的机器人控制系统稳定性分析

蒋圣超，郭丽娟，黄 锋，郭金明，罗传胜，唐 捷

(广西电网有限责任公司 电力科学研究院，南宁 530023)

随着城市化和经济的发展，对电网稳定性的要求越来越高，从上世纪开始，国内外开始研究使用机器人技术完成电力系统的维护任务[1]。协作机器人由于具有人机融合、安全友好等特点，可以作为人类的工作助手与人类协同工作，体现出巨大的技术优势，被越来越多地运用到电力系统维护[2]。在电力应用场景中，对一些复杂的操作，如高压室开关柜相关开关和旋钮的操作、配网线路维护作业等，人直接拖动机械臂末端进行示教会大大简化机器人的应用过程，展现了极好的应用前景。人与机器人在协同作业时，由于人需要与机器人进行力的直接交互，控制系统的稳定性直接关系到控制品质，进而决定作业质量甚至是影响作业成败的关键因素之一，因此对人机协作控制系统的稳定性分析具有十分重要的作用和意义。

作为一种结合机械力量和操作者智能的人机一体化系统，协作机器人研究重点在于对操作者意图的识别和机器人运行的稳定，这些多通过阻抗控制[3-5]或导纳控制[6-7]实现。因此，与人共同作业的协作型机器人的控制算法被广泛地研究；但将协作型机器人与人看做一个整体的控制系统，对这个整体系统稳定性的研究很少被考虑[8]。

在柔顺控制过程中，调整机器人末端的位置(或速度)和接触作用力间的导纳关系，可以实现对机器人位置和接触力的间接控制。研究表明，在导纳控制中对系统稳定性影响最大的因素为环境刚度。 Duchaine V 等[9]提出了一种离线估计操作员手臂最大刚度方法，通过李雅普诺夫理论计算出导纳控制器中至关重要的阻尼参数，但基于最大刚度得到的稳定具有局限性，当操作者放松手臂时导纳参数不能相应减小。Tsumugiwa T等[10]研究通过提高导纳控制的阻尼参数，以减小环境刚度引起的机器人系统的不稳定。

在人机协作机器人系统中，环境刚度即为操作者手臂刚度。在环境刚度较大情况下，导纳控制易造成人机协作系统的不稳定；为稳定系统，通过调整机器人导纳特性来增加阻尼或刚度系数。由于协作型机器人的柔性主要来源于连杆柔性和关节柔性，而连杆可以很容易地通过机械设计来增强其刚度，如利用碳纤维增强连杆刚度，减小其柔性。关节柔性虽然也可以通过机械设计来减小，但效果甚微。文献[11]指出，对于协作型机器人，关节柔性占 80%～95%。因此，本文在参考文献[10]的研究基础上进一步考虑关节柔性，研究系统的稳定性时只讨论具有关节柔性的机器人，而不讨论连杆柔性或双柔性(即连杆柔性与关节柔性)机器人；构建人-协作机器人共同作业的控制系统时，考虑人产生的延时、关节柔性、环境刚度和导纳特性参数，通过仿真进行系统的稳定性分析。

1 人机协作模型

本节建立人-协作机器人系统的导纳控制模型。首先考虑单自由度的导纳控制模型，然后建立电机端力矩和关节连杆端角位置之间的关系，最后构建考虑人的因素和关节柔性的导纳控制模型。

1.1 机器人的导纳控制

为使机器人的单关节拥有如式(1)所示的导纳特性，根据位置进行导纳控制。

(1)

式中：MR、DR、KR分别为导纳特性的惯性系数(kg·m2)、粘性系数(N·m·s/rad)、刚度系数(N·m/rad)；τH为人给机器人关节施加的力矩，N·m；θ为没有考虑关节柔性的电机端位置；Δθ为没有考虑关节柔性时关节的实际位置与平衡位置的差，rad。

1.2 柔性机器人单关节的模型

单柔性关节可被看作为一类简单的二体系统，假设关节柔性具有线性弹簧特性，则其数学模型为

(2)

式中：q为关节连杆端角位置；M、J分别为连杆和电机端的有效转动惯量；K为关节的刚度系数；τm、τf分别为电机端力矩(即控制输入量)和电机端摩擦力矩；τ为由于关节柔性产生的关节力矩。单柔性关节系统的方框图如图1所示。图1中s表示微分算子。

图1 单柔性关节系统方框图

忽略电机端摩擦影响，则从电机力矩τm到θ和q的单柔性关节系统的传递函数如图 2所示。

图2 单柔性关节系统的传递函数

图2中ωa和ωm分别是单柔性关节系统的反谐振频率和谐振频率，表达式为

(3)

1.3 系统模型的搭建

将考虑了机器人关节柔性的连杆位置设为q，可得关于输出q和输入τH的传递函数为

(4)

式(4)中包含了图2所示的以电机位置θ为输入、以连杆位置q为输出的传递函数。将机器人动作的延时设为TR，则考虑机器人动作延时的τH与q的动态关系为

(5)

式(5)也是闭环系统向前通道的传递函数。

考虑关节柔性与外界环境(人)的数学模型如图3所示，下文使用此模型进行校量性分析。

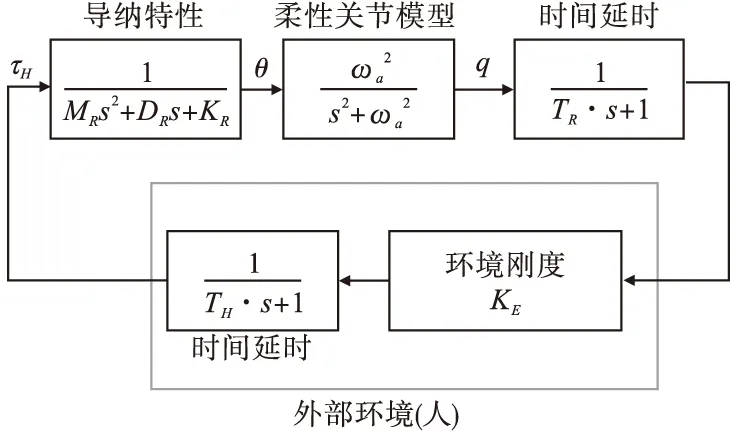
图3 稳定性分析的数学模型

图3中，KE为外部环境(人)的刚度系数；TH为人产生的延时。因此人的传递函数为

(6)

通过式(5)与式(6)可得到式(7)所示的闭环系统的传递函数为

(7)

2 人与机器人协同作业时的控制系统稳定性分析

2.1 控制系统的稳定性分析方法

通过观察闭环系统的极点位置来分析系统的稳定性。分别更改机器人的导纳特性参数，由人的反应时间造成延时和人的刚度系数分析系统的稳定性。当闭环系统的极点在S平面(通过拉普拉斯变换，将时域函数变换到复频域中，并分别以实轴、虚轴为横纵坐标轴组成的平面)的右半平面上时，系统不稳定。

2.2 稳定性分析的仿真

为分析系统的稳定性，进行以下仿真实验。

(a)调节外部环境的刚度系数KE在10～3000N·m/rad的范围内变化；

(b)调节机器人导纳特性的惯性系数MR在0.1～20kg·m2的范围内变化；

(c)调节机器人导纳特性的粘性系数DR在10～1500N·m·s/rad的范围内变化；

(d)调节由于人的反应造成延时TH在0.01～5s的范围内变化；

(e)调节机器人导纳特性的刚度系数KR在10～20000N·m/rad的范围内变化。

为便于分析，设定调节对象为单自由度模型，每次实验时只变化一个参数，其余参数使用以下参数基准值：机器人导纳控制的惯性参数MR=3kg·m2，粘性参数DR=100N·m·s/rad，刚性参数KR=100N·m/rad；外部环境的刚性系数KE为1000N/m。机器人动作延时时间TR设为0.15s，人的反应时间造成延时时间TH设为0.1s；设关节的刚度系数K为11000N·m/rad，关节连杆的转动惯量为5kg·m2，根据式(3)可得ωa=46.9rad。各仿真结果如图4所示。

由图4a可知，外界环境的弹性系数KE变大后，系统变得不稳定。弹性系数KE与其他参数相比对稳定性的影响较大。KE为50、500、1400N·m/rad时，系统的相位裕度和幅值裕度，求出图3的开环传递函数。通过计算开环传递函数波德图，得到KE为50、500、1400N·m/rad时，系统的相位裕度和幅值裕度分别为28.7、8.7、-0.22dB和55.9、44.9、-1.02deg。从图4b可知，通过减小导纳特性惯性系数MR可使系统更加稳定。MR为0.1、7、20kg·m2时，系统的相位裕度和幅值裕度分别为5.99、0.13、-0.338dB和23.7、0.703、-17.3deg。由此可知MR为20kg·m2时系统不稳定。从图4c可知，增大粘性系数DR可使系统更加稳定。DR为70、100、1500N·m·s/rad时，系统的相位裕度和幅值裕度分别为-0.788、2.7、27.6dB和-3.99、13、105deg。从图4d可知，在当前参数设定下，人与机器人共同作业时，由于人的反应时间造成的延时不会对稳定性产生影响。TH为0.01、0.3、2s时，系统的相位裕度和幅值裕度分别为9.54、0.87、5.88dB和35.7、3.76、19.2deg。从图4e可知，即使增加导纳特性的刚度系数KR也不会破坏系统的稳定性。KR为10、1000、10000N·m/rad时系统的相位裕度和幅值裕度分别为1.25、12.6、36.2dB和5.4、60、146deg。

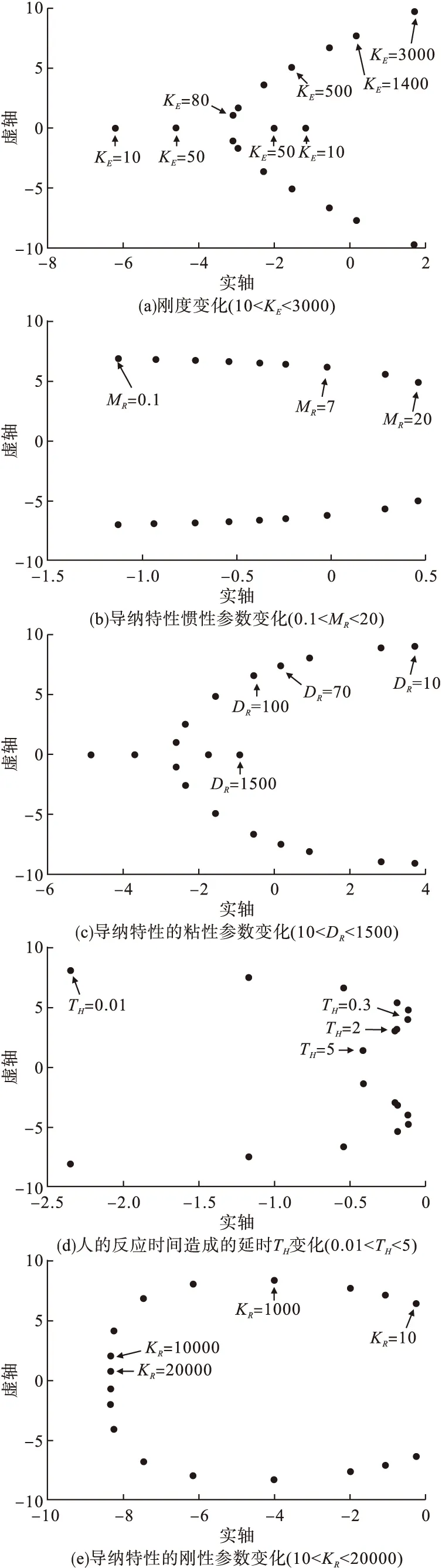
图4 稳定性分析仿真结果

2.3 时域仿真

为验证上节的稳定性分析，进行各参数变化时的时域仿真，仿真结果如图5所示。

图5a是KE为50、500、1400N·m/rad时系统的阶跃响应，从图中可以观察到，随着KE的变化，系统的终值会相应改变，KE在1400N·m/rad附近时系统从稳定逐渐变为不稳定。图5b是MR为0.1、7、20kg·m2时系统的阶跃响应，从图中可以观察到，MR为20kg·m2时系统不稳定。图5c是DR为70、100、1500N·m·s/rad时系统的阶跃响应，从图中可以观察到，DR在70N·m·s/rad附近时系统从稳定逐渐变为不稳定，此结果与上面的稳定性分析结果一致。图5d是TH为0.01、0.3、2s时系统的阶跃响应。图5e是KR为1、1000、10000N·m/rad时系统的阶跃响应，从图中可以观察到，随着KR的增加，系统保持稳定，同时系统的终值会相应改变。

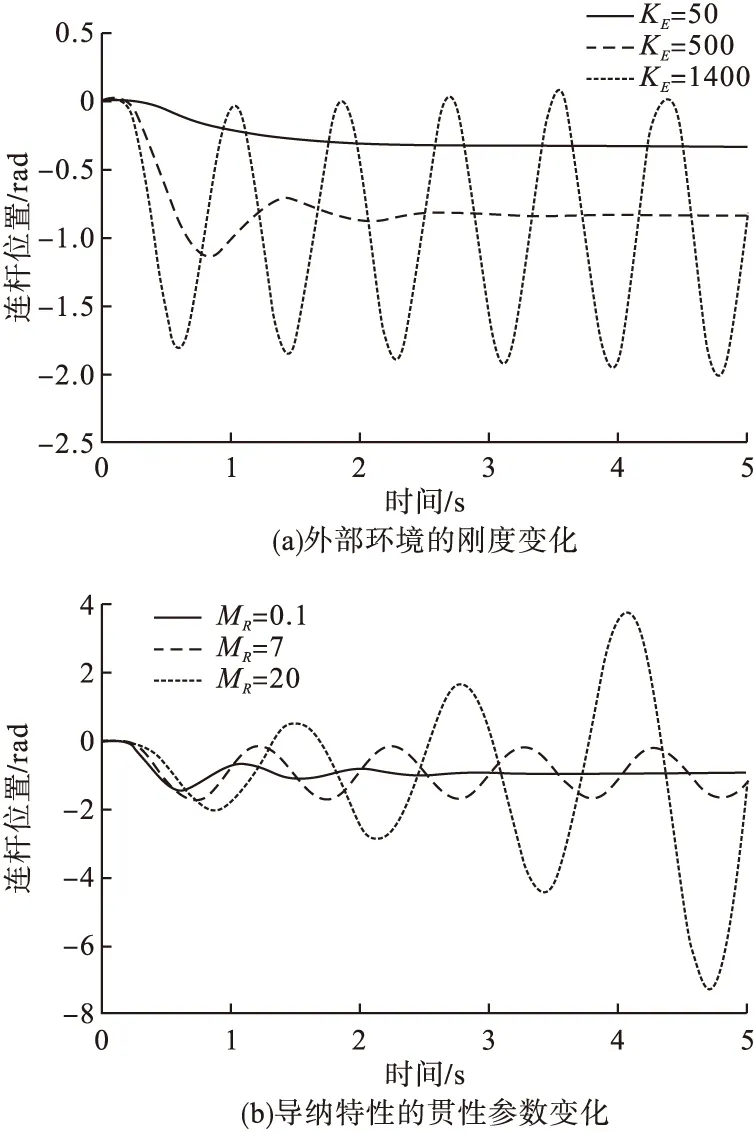
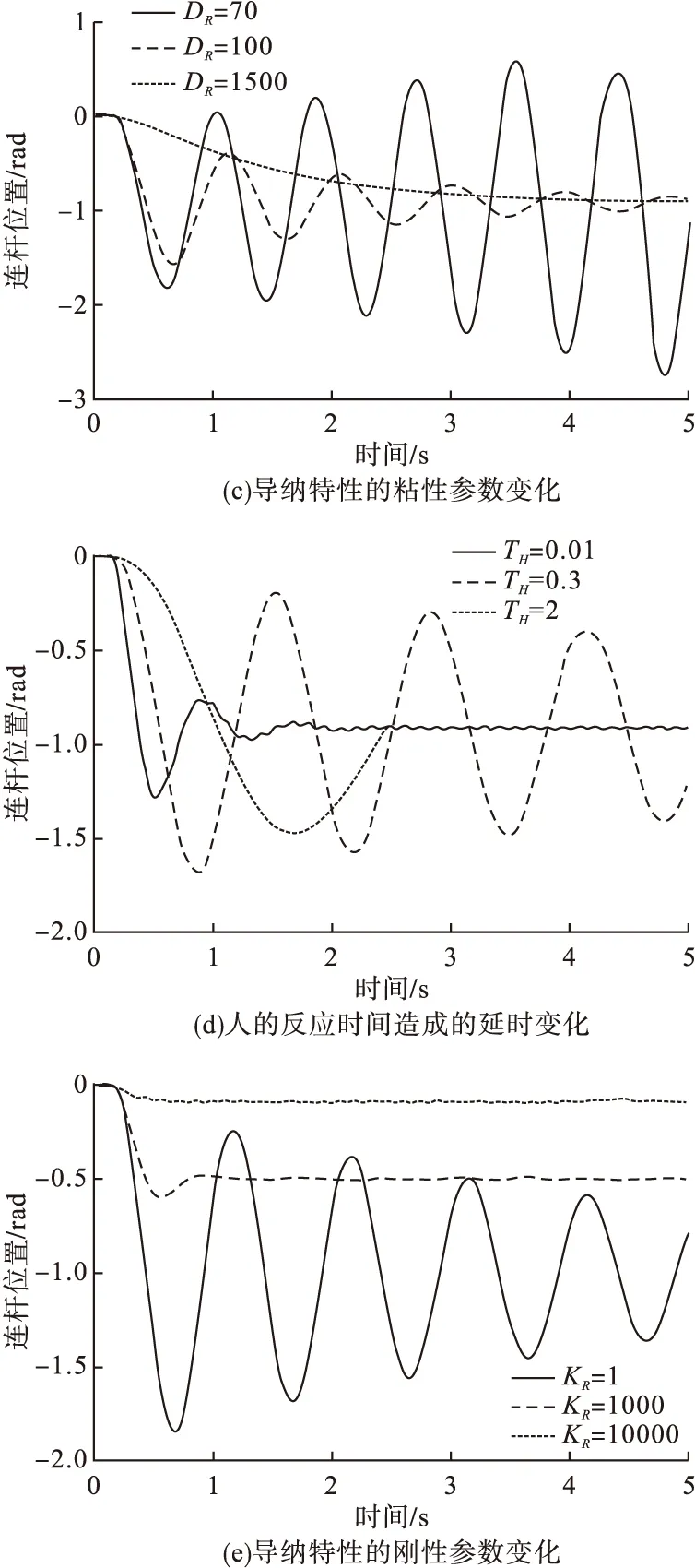
图5 时域仿真结果

3 结论

进行人与协作型机器人共同作业时机器人导纳控制的稳定性分析，分析中考虑了导纳特性、系统延时、环境刚度和关节柔性；分析了系统的相位裕度和幅值裕度，并通过时域仿真验证了稳定性分析结果。结果表明：增加导纳特性的惯性系数、减小粘性系数、增加环境刚度系数会使系统不稳定；导纳特性的刚度系数对稳定性的影响不大。