小学数学教学中浸润数学史的价值探寻

卢伟玲

[摘 要]数学史体现了数学的历史性、科学性和教育性。基于理论研究与教学实践，在小学数学教学中浸润数学史，帮助学生了解数学知识产生的来龙去脉，体会数学思想方法的精髓，获得积极的情感体验，树立学好数学的信心。

[关键词]数学史;价值;小学数学

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）32-0038-02

数学史指的是数学知识产生和发展过程中形成的历史，以及由此形成的数学思想方法与精神等。其具体内涵由三部分组成，一是数学知识产生与形成的过程，体现了数学的历史性;二是数学的思想方法，体现了数学的科学性;三是数学精神，体现了数学史的教育性。数学史是数学文化的重要组成部分，在教学中，教师以数学史为载体渗透数学文化，将数学发展的辉煌成就、数学家传记、趣事逸闻等资料展示出来，可以帮助学生了解数学知识产生的来龙去脉，体会数学思想方法的精髓。本文论述了在小学数学教学中浸润数学史的价值和策略，期望对广大教育同仁有所借鉴和思考。

一、浸润数学史，激发兴趣树立信心

学习兴趣对于数学学习具有重要作用。在教学中浸润数学史，是激发学生学习数学兴趣的有效路径。教师如果能够结合教材内容，为学生提供一些与教学内容密切相关的数学史的知识，使学生了解数学知识产生和发展的历程，就能活跃课堂气氛，使学生感受到数学的奥妙和神奇，使学生感受到数学的魅力，激发学生学习数学的兴趣。

比如，在教学“认识钟表”一课时，教师利用多媒体为学生展示了计时工具的演变过程：“在原始社会，人们白天外出打猎，晚上回到山洞中休息，因此，原始人只知道用“日”和“夜”来计算时间。后来，人们通过观察一天中影子的长度和方向来大致确定时间，即立竿测影或日晷测影，人们对时间的认识有了很大进步。随着社会的发展，人们对时间精度的要求越来越高，这时人们学会了利用漏沙或者滴水的办法来计算时间，这就是滴漏计时。再后来，随着科学技术的逐步发展，人们发明了钟表，人们认识和计算时间的精确度越来越高。”学生纷纷为前人的智慧和创造性所折服，学习兴趣和探究热情被充分激发。随后，教师用多媒体展示国内外各种各样的钟表图片，学生通过观察和比较，发现尽管钟表的外形、大小各不相同，但是所有的钟表都有时针、分针等构成要素，由此对钟表的构成有了初步的印象和理解。

教学中，教师以多媒体的形式，通过展示一些生动活泼的数学史料和图片，激发了学生认识钟表的兴趣，为枯燥单调的数学课堂加入了一些趣味，从而激发了学生学习数学的兴趣，帮助学生树立学好数学的信心。

二、浸润数学史，厘清数学知识发展脉络

数学史蕴含了数学产生和发展的历史脉络，是数学观念、数学思想方法的集中体现。在数学课堂中浸润数学史，展开对数学知识的追根溯源，可以使学生了解数学知识产生和发展的真实过程，可以帮助学生厘清数学知识发展的基本脉络，由此加深学生对数学知识的整体性理解，使学生体会到数学在人类历史发展中的重要作用，让学生更加欣赏数学、喜欢数学。

比如，在教学“圆的周长”时，教师引导学生追溯了人们认识圆周率的发展历程：“在远古时代，制作车轮的师傅需要知道在车轮直径一定的情况下，需要用多长的木条才能做出符合要求的轮子，这个时候，人们已经知道了轮子转一圈的长度和它的直径之间存在某种联系。2000多年前，中国古代数学著作《周髀算经》中就有‘周三径一的记载。伴随着社会的进步，人们对圆周率的精度要求越来越高。魏晋时期的数学家刘徽发明了‘割圆术。‘割之弥細，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。正是通过‘割圆术，刘徽计算出圆周率为3.1416。南北朝时期著名数学家祖冲之计算出圆周率应在3.1415926和3.1415927之间，这项成就领先了其他国家1000多年。电子计算机的出现带来了计算方面的巨大变革，圆周率小数点后面的数字被知道的越来越多。2010年9月17日，有人采用“云计算”技术，利用1000台计算机同时计算了23天，将圆周率精确到了小数点后2000万亿位，刷新了人们对圆周率的认知。”

教学中，教师为学生呈现了人们探索圆周率的过程，使学生厘清了圆周率发展的来龙去脉，加深了学生对圆周率的整体性认识，为单调乏味的数学课添加了一些“文化味”。

三、浸润数学史，领悟数学思想方法

数学的灵魂是数学的精神和思想 。数学课程标准指出，学生应该在数学学习中“获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验”。数学史既是数学知识产生和发展的历史，也是数学思想方法产生和发展的历史。教师可通过挖掘数学史中蕴含的数学思想方法，并有目的地将其渗透于数学课堂的教学之中，引导学生运用数学思想方法来思考问题，可以加深学生对数学知识的认知深度，提升学生分析问题和解决问题的能力。

比如，在“圆的面积”的教学中，大多数教师引导学生运用转化思想和极限思想推导出圆的面积公式。其实，我国的数学著作《周髀算经》中提出了“圆出于方”的观点，为推导圆的面积计算公式提供了思路：

师：同学们，你们知道“圆出于方”是什么意思吗？

生1：圆是由方得来的。

（教师出示图片）

师：你能看懂这幅图吗？

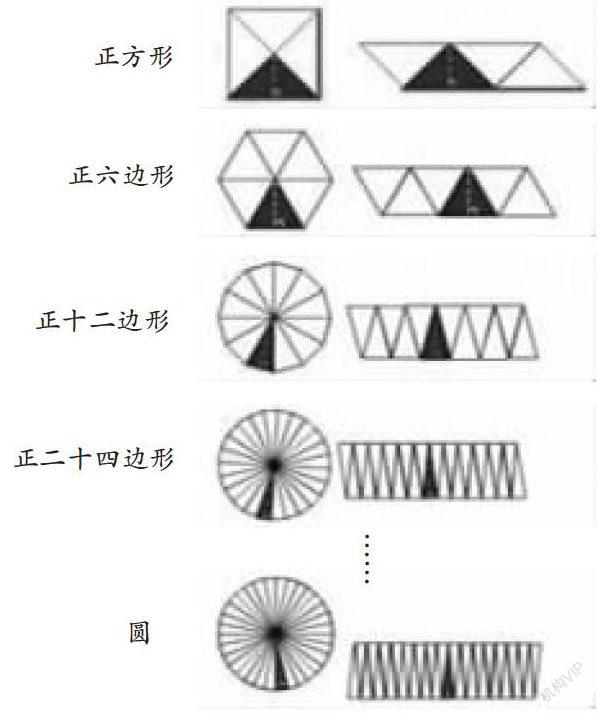
生1：圆的确是由“方”得来的。你看，正方形、正六边形、正十二边形、正二十四边形……直至得到一个圆。

师：你能看懂圆的面积推导过程吗？

生2：把正方形平均分成4份，然后拼接成一个平行四边形，平行四边形的底是正方形周长的一半，平行四边形的高是半径（把正方形看作圆），所以，正方形面积S=[C2]×h;把正六边形平均分成6份，然后拼接成平行四边形，平行四边形的底是正六边形周长的一半，平行四边形的高是半径（把正六边形看作圆），所以，正六边形的面积S=[C2]×h;以此类推，得出圆的面积S=[C2]×h。这里的C指的是圆的周长，h指的是圆的半径。因此，圆的面积=2πr÷2×r=πr2  。

生3：這种推导方式真奇妙呀。

师：“圆出于方”的观点不但阐释了“圆”的来源问题，而且可以将其运用到圆的面积公式的推导当中。

教学中，教师以“圆出于方”的观点为指导，引导学生把圆类比成正多边形，先推导出正偶数边多边形的面积公式，然后用类比的思想推导出圆的面积公式。在探究的过程中，学生体验到“圆出于方”这一思想的精髓，加深了对圆的本质的理解。

四、浸润数学史，获得积极的情感体验

学生学习数学的过程并非纯粹的理性认知过程，而是一种有温度的情感、文化认知过程。只有拥有深厚的文化素养、底蕴，对数字的认知才不会偏离航道。数学学科经历了漫长的发展过程，在这个过程中出现了各种困难和问题。教学中，教师可以将这些困难和问题作为素材引入课堂进行情境再现，让学生体验到历史上数学家追求真理、百折不挠的精神，从而使学生获得积极的情感体验，培养学生学习与探究热情，磨炼学生的坚强意志。

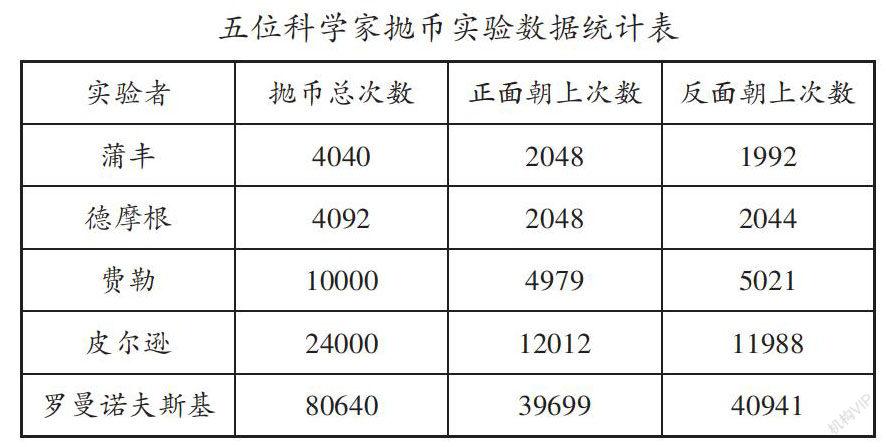
比如，在教学“统计与概率”时，教师组织学生两人一组玩抛币游戏，一名学生抛出硬币，另一名学生负责统计硬币正面朝上和反面朝上的次数，最后两人共同探寻其中的规律。有的小组抛币10次，有的小组抛币20次，有的小组抛币30次，通过分析数据，学生得出结论：“硬币正面朝上和反面朝上的次数是相近的。”教师追问：“如果抛币100次、1000次、10000次呢？”随后教师为学生出示五位科学家抛币的实验数据表（如下表），学生通过分析表格不但得出了“实验次数越多，正面朝上与反面朝上的次数越接近”的结论，更为重要的是，学生都被科学家这种一丝不苟、求真务实、持之以恒的精神所折服，由此培养了严谨求实、刻苦钻研的数学精神。

课堂上，学生通过玩抛币游戏，初步体会到硬币正面朝上和反面朝上是等概率事件。在此基础上，教师为学生展示五位科学家成千上万次的抛币实验数据，使学生在获得数学结论的基础上，感受科学家刻苦钻研、严谨求实的精神，从而使学生获得积极的情感体验。

数学史是人类文明发展史的重要组成部分，我们要继承和发扬数学史中蕴含的科学精神和文化品质，在课堂中适当地融入与数学主体相关的数学史料，通过展示数学知识的来龙去脉，呈现数学家探索真理的过程，让数学史发挥“师者”的作用，让学生在与古人的对话中获得知识源泉，汲取精神营养。

（责编 吴美玲）