多元表征：让数学思维可见

束枫林

（江苏省盐城市经济开发区教师发展中心）

北京市特级教师华应龙老师在“我不是笨小孩——以‘师徒年龄问题’为例”一课的教学中，妙用“投石问路”，实现了“直观操作思维—表象思维—算术思维—代数思维”四个思维阶段的顺利衔接。而后，华老师在课后反思中这样写到：“数学家之所以能在工作中攻克一个又一个难关，一个重要方面是他们能够将问题在各种各样的数学表达式间灵活转换，这些数学表达方式包括符号、语言、图形、表格、图表等。”这其中，符号、语言、图形、表格、图表等多种表达方式，即为数学内容的多元表征。在数学教学中，让学生用数学思维去思考和解决问题一直是难点。由于年龄特点，小学生的思维仍处在由直观思维向抽象思维的过渡阶段。因此，作为教师，应当在教学中采取多元表征的形式，让数学思维能够以学生“可见”的方式，帮助他们去理解和掌握知识，发展数学能力。

一、恰当呈现，让知识内核“看得见”

呈现学习对象多元表征，是指通过言语、操作、图形、数据、符号等表征从不同的视角运用不同的方式、不同的手段呈现数学对象，并引导学生分层次、逐步地抽象数学学习对象。经由多元化呈现后，数学知识的非本质属性得以逐步剥离，学生理解数学知识的本质、实现数学意义的多元建构自然而然，从而让知识内核真正“看得见”。以“加法交换律”一课为例，加法交换律的内容可以用以下四种方式表征。（如表1）

表1 “加法交换律”内容表征方式

其中，以数据列举的形式呈现加法交换律，学生很容易在头脑中建构起加法交换律的数据表征，以便发现交换律的外部特征，理解交换律的外延，意义建构得以实现；而以动画操作和图形的形式呈现交换律，学生自然会在头脑中建构交换律的图形表征，同时，这样的图形表征又为他们建构交换律的文字表征以及符号表征提供了感性经验支撑，使得理解交换律的本质内涵更容易，意义建构水到渠成。

值得注意的是，数学学习对象的呈现一定要围绕数学本质选择恰当的方式，不可盲目认为方式越多越好。要以相互映衬、相互补充、相互解释的原则恰到好处地择机呈现，做到形不同而质相同。这样，才能在丰富的数学多元表征下构成数学学习对象的网络结构，让知识内核真正“看得见”。

二、巧妙勾连，让思维方法“看得清”

数学知识体系是一个有机的结构性整体，数学教学中，教师要抓住数学表征内在的多元联系，引领学生实现数学学科内容各种表征内部的灵活转换和表征之间的灵活转译，促使学生灵活提取数学知识并应用于实践，让思维方法“看得清”。这既是实现学生数学知识学习由认识到理解的重要标志，又是数学素养生成的重要标志。

以“认识面积单位”一课为例，教学“1平方厘米”时，可以采用视觉表征的形式，让1平方厘米的正方形纸片贯穿教学始终。

首先，我让学生拿出准备好的1平方厘米纸片，明确其面积就是1平方厘米，使得学生对1平方厘米有一个直观感知。其次，再让学生用直尺量一量它的边长，并交流：“1平方厘米的正方形的边长是多少厘米？”在这一环节，学生通过测量，把视觉表征转译成“边长为1厘米的正方形，面积就是1平方厘米”的语言表征。最后，我引导学生通过“摸一摸”“比一比”“找一找”等多种方式对1平方厘米形成表象，让他们到生活中找寻1平方厘米的实物。学生有了具体的视觉表征和准确的语言表征后，很自然地找出了许多生活中的1平方厘米大小的实物，从而在脑海里留下了关于“1平方厘米大小”的深刻表象。这样，通过勾连视觉、语言、记忆三种表征之间的相互转译、互换，使得学生理解1平方厘米及面积单位的含义的思维方法一目了然。

三、内外融合，让思维过程“看得深”

如何将看不见、摸不着的数学思维可视化？一个重要的方式就是恰当融合数学学习对象的内化表征和学生数学思维的外化表征，以构成学生的生态学习循环系统，让他们的思维过程“看得深”。

以“解决问题的策略——假设”一课为例，教材中有这样一道例题：

小明把720毫升果汁倒入6个小杯和1个大杯，正好都倒满。已知小杯的容量是大杯的，小杯和大杯的容量各是多少毫升？

把这道题以问题表征的形式呈现给学生后，我先引导他们将自己内心对学习对象加工的思维表象，用恰当的方式转译成可视性表征。这时，发现了学生多元的个性化外部可视表征。

如有的学生用直观形象的模拟图表征。（如图1、图2）

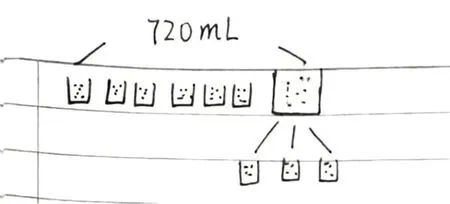
图1

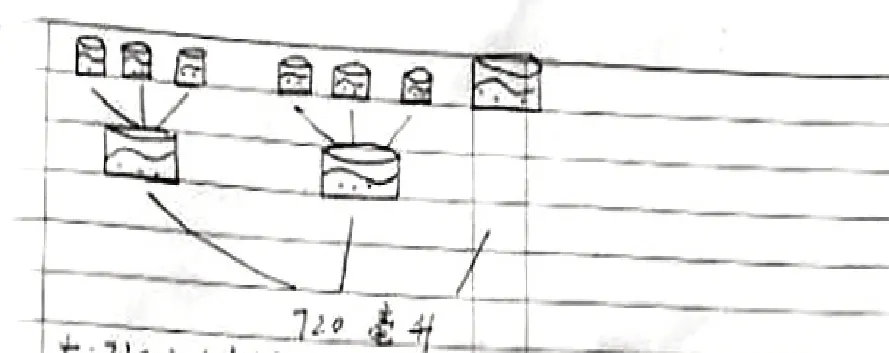
图2

有的学生则用更高抽象思维水平的线段图表征、言语文字表征（如图3、图4）

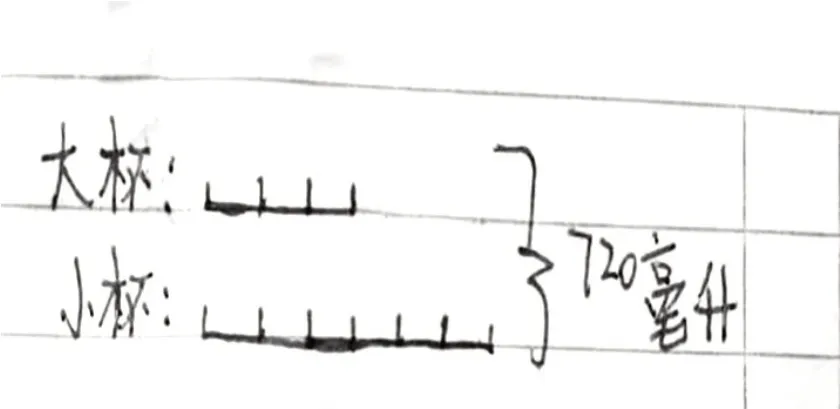
图3

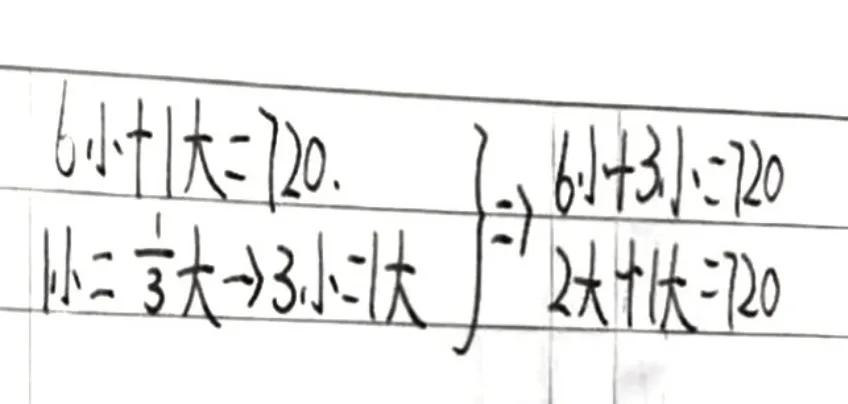
图4

在学生对学习对象的思维表象转译成可视的模拟图表征、线段图表征、言语文字表征后，紧接着，我引导他们更深入地将理解加工后的问题表征进一步转译成算式表征，又发现了学生不同的思维外显。（如图5、图6、图7、图8）

图5

图6

图7

图8

观察学生的算式表征，他们的思维过程一览无遗：如图5、图6、图7、图8，他们是利用分数和比之间的联系，先将“小杯容量是大杯的”转化成“小杯与大杯容量之比是1∶3”。以此，将大、小杯的个数进行灵活转化并替换成一种杯型的后列式来解答。图5是把6个小杯换成2个大杯，这样720毫升的果汁就相当于倒满3个大杯，就可先列式求大杯的容量，小杯容量也就迎刃而解。图6是把1个大杯换成3个小杯，720毫升的果汁就相当于倒满9个小杯，于是先列式求小杯的容量，大杯容量同样顺利得解。而图7、图8，学生则是运用了方程的思想，根据“小杯的容量是大杯的”或把大杯容量设为x毫升，则小杯容量就是毫升，或把小杯容量设为x毫升，则大杯容量就是3x毫升，然后再根据“把720毫升果汁倒入6个小杯和1个大杯，正好都倒满”列方程顺利解决了问题。

由此可见，同样的问题，不同学生内化后所外化出来的表征是不同的，在这样一个“内化—外化—再内化”的融合中，我们可以看出学生不同的认知风格以及不同深度的思维水平。

总之，数学多元表征的恰当呈现、互换互译、内外融合能够让学生的思维可见，让数学学习真正落地，能够有效实现数学素养的整体提升。作为教师，我们应恰当将数学的多元表征学习融入到平时的数学课堂教学中，实现深度学习，发展综合学力。